基于欧拉迭代模型预测的欠驱动水面船舶路径跟踪控制

李荣辉，陈志娟，李宗宣，卜仁祥

（1.大连海事大学航海学院，辽宁 大连 116026；2.广东海洋大学海运学院，广东 湛江 524088）

由于欠驱动船舶运动具有模型不确定、受外界干扰以及舵角输入受约束等特性，所以对其路径跟踪控制是比较复杂的。Fossen 提出Line of Sight（LOS）制导法[1]，将路径跟踪三维控制转换为对船首向角的一维控制。文献[2-3]在滑模控制中结合增量反馈，避免对不确定项进行估计。文献[4-6]利用自抗扰控制器的核心（即扩张状态观测器）对内部未知项和外部扰动进行估计。文献[7]利用神经网络进行参数优化，避免不确定项和外界干扰。文献[8-10]均采用自适应算法对外界干扰进行处理。文献[11]设计最小二乘法与神经元自适应相结合的控制器，使船在风浪流干扰下仍能跟踪上曲线航迹。文献[12]将Lyapunov 直接法和神经网络结合，使船在外界干扰下仍能跟踪上正弦路径。文献[13]提出结合 backstepping 与径向基函数（radial basis function，RBF）神经网络的简捷鲁棒自适应控制器，有效地解决风浪流干扰。文献[14]为防止所计算的控制律超出约束范围，便引入辅助系统。文献[2]利用双曲正切函数本身的极值约束性对舵角输入进行了限制。文献[15]提出模型预测控制（model predictive control，MPC），使船能在有风流的环境中跟踪上参考路径。文献[16]设计了轨迹跟踪MPC控制器，能同时处理输入及输入增量约束。文献[17]提出线性和非线性MPC，线性MPC 在计算量上更小却在控制精度上不如非线性MPC 高，但两者均能有效地处理约束问题。

从以上研究可以看出，对处理外界干扰及模型不确定项的研究已多有成果，而对于舵角约束处理的方案则较少。在舵角约束方面，本研究考虑到MPC 只需在求解二次型（Quadratic Programming，QP）[18]时加入舵角的限制值，便可自然地解决舵角约束问题，因此提出一种欧拉迭代MPC 控制算法，对船舶路径跟踪进行控制。多数MPC 算法是将卷积模型或状态空间模型作为预测模型，来预测未来状态值[16,19]。而船舶实际模型中各个状态之间都是高度耦合的，需要对其简化处理。本研究为提高预测精度，采用分离型船舶模型（mathematical model group，MMG）作为预测模型，与简化后的船舶模型相比，MMG 与实际船舶运动情况更为符合。由于MMG 非线性和耦合程度较高，所需船舶参数较多且计算量大，因此本研究采用欧拉迭代法对MMG 模型进行离散并预测，并通过仿真结果验证所提控制器的有效性。

1 船舶路径跟踪控制数学模型

分离型模型（MMG）是基于深层次的理论分析结合大量的试验进行研究的，其将作用于船舶上的流体动力和力矩分解为作用于船体、螺旋桨和舵上的流体动力和力矩，并考虑各流体动力和力矩之间的相互影响[2]。船舶在平面内的位置与运动参数的关系如图1 所示。

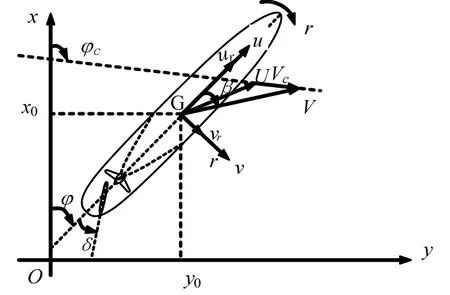
图1 在流干扰下的船舶平面位置与运动参数Fig.1 Planimetric position and kinematicswith of ship under current disturbance

其中，在空间固定坐标系中，船舶重心在固定坐标系的位置用x0、y0表示，规定x轴指向正北，船首尾中心线与x轴的夹角即船首向角用φ表示。φc和Vc分别为流的流向和流速，ur为对水前进速度，vr为对水横移速度，对水合速度U=(ur2+vr2)1/2。船舶运动速度在oxyz坐标系上沿x轴和y轴上的分量分别为u和v，u为对地前进速度，v为对地横移速度，船首绕z轴旋转的角速度为r，对地合速度V=(u2+v2)1/2，漂角β=arctan(v/u)，δ为舵角。由图1，考虑了风、浪、流干扰和舵机响应特性的船舶MMG 模型如下：

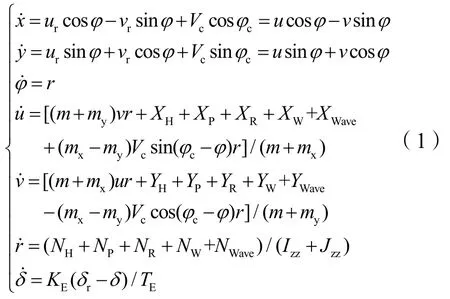
式中，δr为命令舵角，KE为舵机控制增益，TE为舵机时间常数，m为船舶质量，mx和my为附加质量，XH、YH和NH为作用于船体的黏性类流体动力（矩），XP、YP和NP为螺旋桨力(矩)，XW、YW和NW为风力(矩)，XWave、YWave和NWave为浪力(矩)，IZZ为船舶绕竖直轴的惯性矩，JZZ为附加惯性矩。XR、YR和NR为舵力(矩)，其计算公式如下：

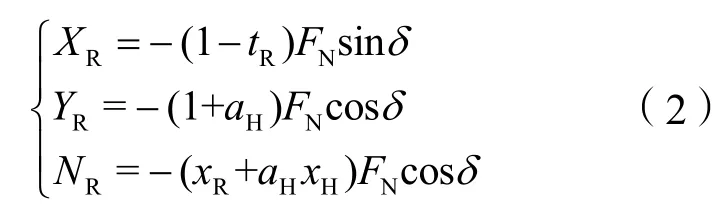
式中，tR是舵阻力减额份数，aH是操舵引起的船体附加横向力与舵横向力的比值，xH是操舵诱导船体横向力作用中心到船舶重心的距离，FN是舵正压力。

本研究假设所有船舶系统状态值x，y，φ，u，v，r均可被获取到。给定螺旋桨转速，只对横向位移进行控制，控制目标是设计合适的舵角，使船舶跟踪参考路径。

2 路径跟踪控制器设计

2.1 MPC 控制器

本研究将MPC 作为路径跟踪控制器，MPC 算法包括预测模型、反馈校正、滚动优化三个要素[20]。它的主要优点是只需通过在约束下计算标准的QP二次型，便可直接解决系统输入限制的问题。首先，根据预测模型和当前系统状态来对预测时域Np内的所有未来状态进行预测。然后，建立包含预测误差在内的优化函数。最后通过在有约束下求解此优化函数，便可计算出最优控制输入。到下一时刻，利用系统新的测量数据的反馈，重复相同的流程，即滚动优化。本研究直接将MMG 模型作为预测模型，并基于欧拉迭代法对系统状态进行离散和预测。控制结构如图2 所示。

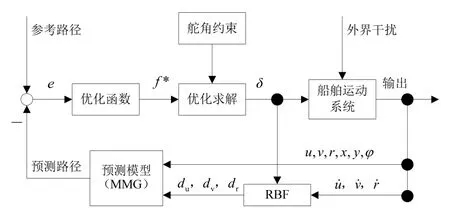
图2 船舶路径跟踪MPC 控制设计结构Fig.2 Structural diagram of MPC for ship path following

在当前时刻，船舶运动系统输出当前状态值，RBF 神经网络通过状态历史信息对未知干扰项进行逼近。然后，根据预测模型和当前状态对预测时域Np内的所有未来状态进行预测。利用预测路径与参考路径之间的预测误差建立优化函数。最后通过在有约束下求解此优化函数，可计算出最优控制舵角。待下一时刻，船舶运动系统继续将状态值反馈给控制器，进行滚动优化，以此类推。

对式（1）中的各个状态进行离散和预测，式（1）中动力学微分方程中的各个力矩之间是高度耦合的，很难转化为状态空间矩阵形式，即不能通过矩阵进行预测。本研究采用欧拉法[21]，通过各个状态之间的迭代，在保留原来各状态之间耦合及非线性关系的基础上进行预测：

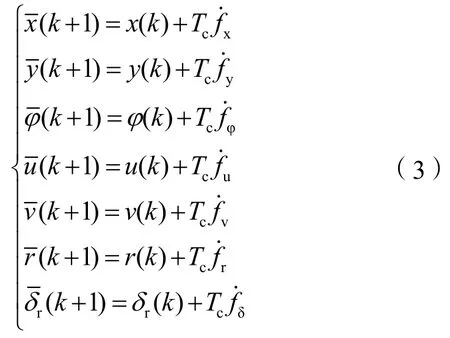
式中，Tc是预测采样时间，即连续两个预测值之间的时间间隔。和分别是对式（1）中各微分方程的离散化，计算公式如下。

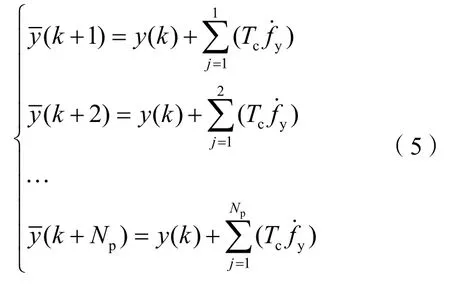
通过式（5）的预测结果和参考横向位移yd，计算路径预测误差其中j=1，2，…，Np。

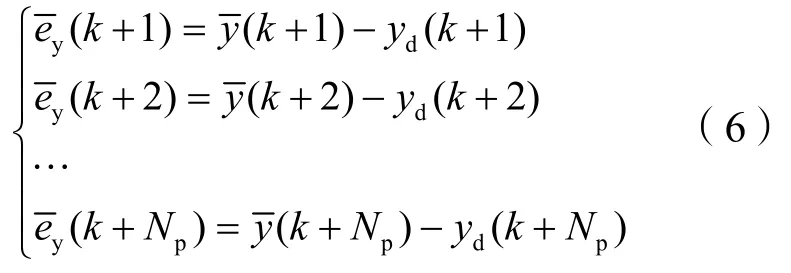
根据预测误差，构造优化函数如式（7）：

式中，Q是权重矩阵，通过求解QP 二次型或者在约束条件δmin≤δ≤δmax下求解方程∂f*(ēy,δ)/∂δ=0，可以计算出最优控制律δ*。由于MPC是利用计算机在线进行运算的[22]，所以只能在线通过每步优化来计算控制律，而不能直接写出控制律的解析式。对于优化函数中所包含的未知干扰项，利用RBF 进行逼近并补偿。Np是预测时域，Nc是控制时域，即在预测系统未来状态时需要的未来输入个数δk+1，δk+2，…，δk+Nc。Np、Nc和Tc作为控制参数，需要进行设计。其稳定性分析如下：

引理1：当h(x)在两端点a、b处的函数值A、B 异号时，在开区间（a，b）内必存在至少一点ξ，使h(ξ)=0。

引理2[23]：一个函数能够取到极值的充要条件：（1）存在使导数等于0 的点；（2）使导数等于0的那个x值，左右两边导数符号相反。

由式（1）、（2）、（3）和（4），有

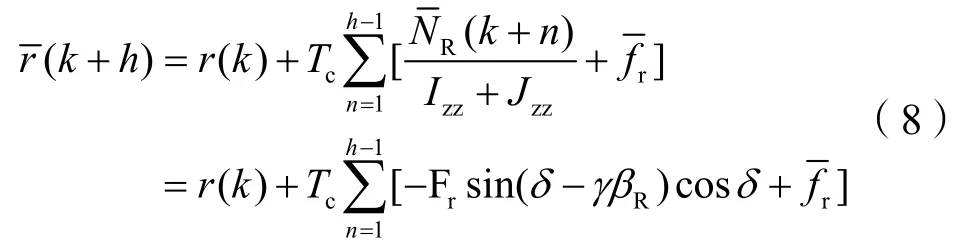
式中，Fr为正的不含舵角的常系数，为不含舵角的其它项总和，γ是整流系数，与βR的值如下：

式中，L是船长，Cb是方形系数，B是船宽。船舶在正常行驶时，船速为常速且漂角不太大，本研究取|β|≤25°，U≤7.5 m/s，转首角速度|r|≤3°/s。将式（8）对δ求偏导，式（8）为差分方程，本不可以对其求导，本研究视其为各个时刻连续值的累加和，通过对每个时刻偏导数的累加来求近似整体的偏导数。并根据船舶参数可得：

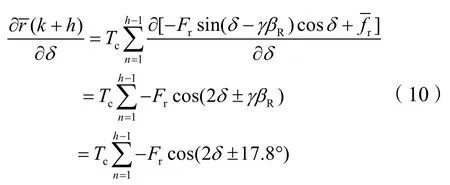
由式（3）和（4），有

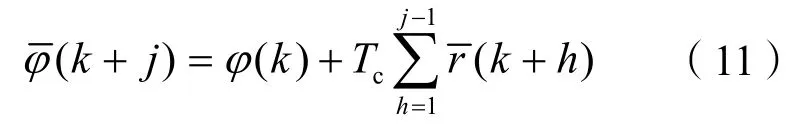
将（11）对δ求偏导，并把式（10）代入，得

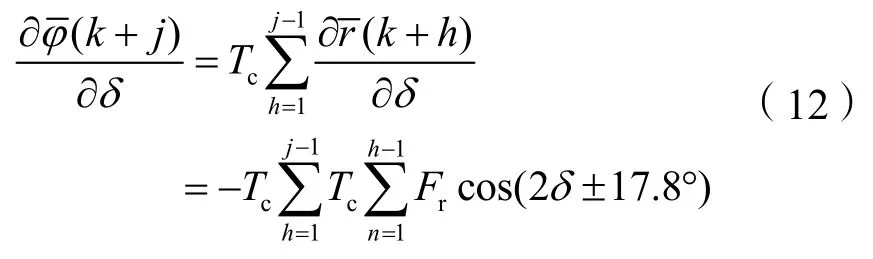
对式（4）第2 项做三角函数变换，得

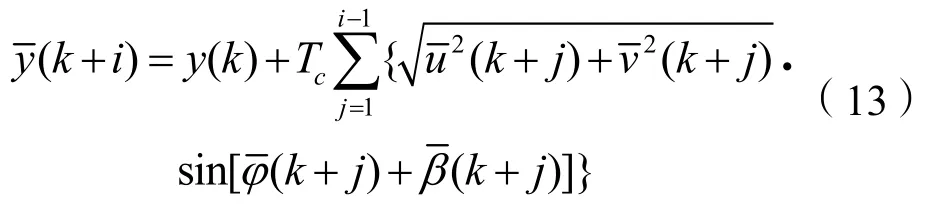
将式（14）对δ求偏导，由于参考位移yd不含舵角δ，并且舵力在速度u、v上的分量相对于在转首角速度上的十分小[24]，所以忽略它们对舵角的导数，则有

式中，z1、z2以及z3如下：

由于舵角|δ|≤35°，所以z3恒小于零。将式（8）和（11）代入式（16）最后一项，有

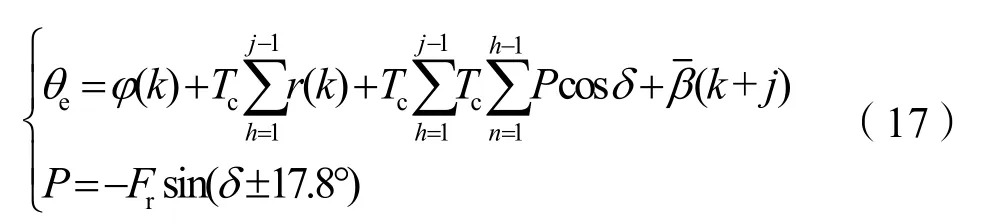
由于舵角|δ|≤35°，所以cosδ＞ 0。h、j和i的大小均受预测时域Np限制。由于漂角较小且船首向角初始值是定值，故θe的符号和大小仅取决于δ、Np和Tc。因此，设计合适的控制参数Np和Tc便可以使式（15）有如下变化：

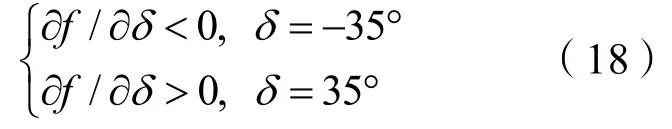
由于船舶运动过程是连续的，所以f也是连续的。则根据式（18）和引理1，存在最优舵角δ*可使∂f/ ∂δ=0。并且，当δ＜δ*时，∂f/ ∂δ＜ 0，当δ＞δ*时，∂f/ ∂δ＞ 0。则根据引理2 可知，f在δ*处取极小值，则每一时刻滚动求解δ*，使f与(k+j)通过每次得最小值而逐渐趋于零，从而使得y逐渐跟踪上yd。

2.2 RBF 神经网络

本节利用船舶历史信息（即上一采样时刻的船舶输出状态值）和RBF 的梯度下降法训练权重值，使RBF 的输出逼近外界未知项[25]。以(k) 为例，设计过程如下：

式中yn是RBF 输出，即(k)，m 是神经元数，w是权重，h是隐含层输出，计算如下：

式中，x是输入，即[δ，]，cj是中心点矢量值，bj是宽度矢量值，计算如下：

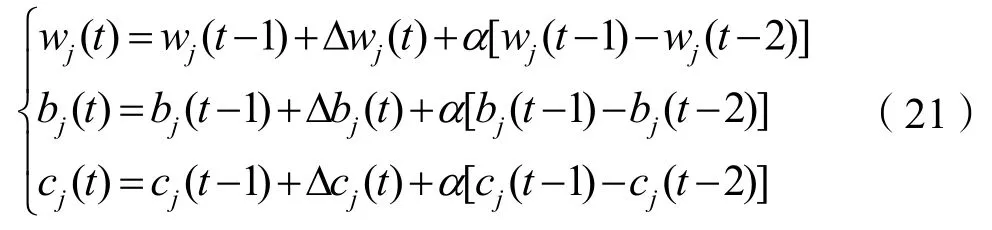
式中，α∈(0，1) 是动量因子，利用梯度下降法调节w、b和c，计算如下：

式中，η∈(0，1) 是学习速率，yh是船舶历史状态信息与控制器中对应的水动力之间的误差数据，E为逼近偏差。通过误差数据的训练，可以使RBF逼近船舶实际系统状态与控制器中所用模型之间的偏差，即外界干扰项，用来补偿MPC 中的预测模型。当外界为定常干扰时，最终权值会稳定。本研究为处理时变干扰，每隔3 个采样时间便对RBF训练一次。逼近流程与相同。

3 仿真验证与分析

为验证所设计控制器的有效性，以大连海事大学实习船育龙轮为仿真对象，在MATLAB 中进行仿真[26]，以式（1）中MMG 模型为仿真模型。育龙轮参数[27]：满载吃水8 m，满载排水量14 635 t，船长126 m，船宽20.8 m，方形系数0.681，正面受风面积369.9 m2，侧面受风面积1031.94 m2，螺旋桨直径4.6 m，螺距3.66 m，舵面积18.8 m2，展弦比1.72，舵机时间常数TE2.5 s，设定螺旋桨转速100 转/分钟。

仿真1：初始状态：u=7.2 m/s，v=0，r=0，φ=0，(x0，y0)=(0，200 m)；外界干扰，风速：10m/s，风向：30°sin(0.02t)+45°；流速：1.0 m/s，流向：10°sin(0.005t)+45°；控制器参数：Np=18，Nc=1，Tc=2.0 s；RBF 参数：η=0.15，α=0.05，c0=[-1 -0.5 0 0.5 1;-1 -0.5 0 0.5 1]，b0=5，w0=0。

由图3 可看出，船舶路径产生了小于7%的超调，但都小于船宽20.4 m。系统稳定后，由于时变干扰的影响，所以路径一直存在小波动，但波动的最大幅值也小于5 m，即不到船宽的25%，这在实际航行中属于正常。因此我们可以认为船舶在受到风流时变干扰的情况下，所设计控制器仍能使船准确地跟踪上直线参考路径。所用仿真实验船本身的舵角幅度限制值为35°。由舵角变化可以看出，在系统稳定后，由于时变风流干扰的影响，船首向角与舵角时刻变化，以抵抗时变外界干扰。但船首向角和舵角变化平稳，舵角幅度限制在10°以内，验证了所提MPC 控制器可有效处理舵角约束。

仿真2：初始状态u=7.2 m/s，v=0，r=0，φ=0，(x0，y0)=(0，0)；参考路径：yd=200sin(0.00035πx)；外界干扰，风速：10 m/s，风向：30°sin(0.01t)+45°；流速：1.0 m/s，流向：10°sin(0.005t)+45°；控制器参数：Np=15，Nc=1，Tc=2.5 s，RBF 参数与仿真3相同。

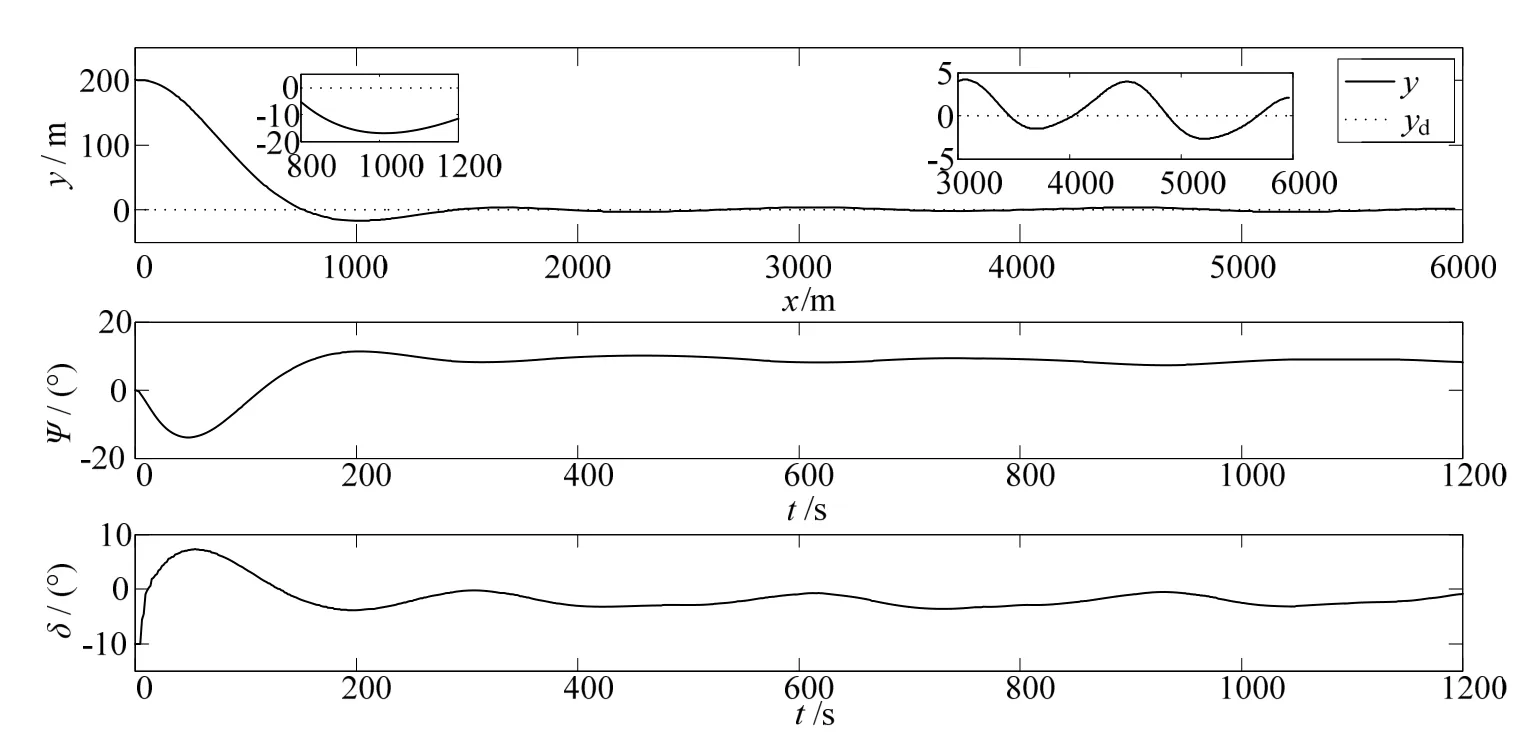
图3 有风流干扰的直线路径跟踪Fig.3 Straight line path following with wind/current disturbances

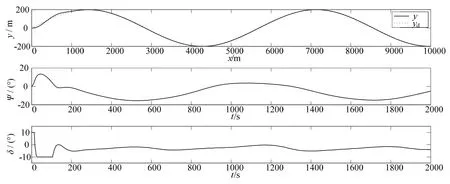
图4 有风流干扰的曲线路径跟踪Fig.4 Curve path following with wind/current disturbances

由图4 可以看出，在风流时变干扰下，船舶仍能准确地跟踪上曲线路径。从舵角的变化可以看出，整个过程中舵角都被限制在较小的范围，并且光滑没有振荡或抖动。曲线路径跟踪与舵角变化的结果，说明了所设计的控制器能有效处理曲线跟踪过程中的外界干扰以及舵角约束问题。

4 结论

本研究考虑欠驱动船舶在运动过程中具有受外部风流干扰、控制输入受约束等问题，基于欧拉迭代法设计了船舶路径跟踪MPC 控制器。利用MPC 本身在处理系统约束问题上的优点，解决了舵角输入受约束问题。并采用欧拉迭代法离散并预测船舶未来状态，以保留船舶运动状态之间的非线性和耦合性并简化MPC 的运算量。直接以MMG 船舶运动模型作为MPC 的预测模型，弥补了欧拉迭代法精度的不足。利用径向基函数神经网络通过历史信息的训练，对外界干扰进行逼近及补偿。仿真结果表明所设计的MPC 控制器使船舶在外界干扰下仍能准确地跟踪上设定的路径，舵角变化小，光滑平稳。在风流时变干扰的情况下，控制舵角被限制在较小的幅度范围内，说明了所设计MPC 控制器可以有效处理舵角约束问题的能力。