基于扫描线的卫星区域覆盖分析算法

汪荣峰,胡 敏

(航天工程大学 航天指挥学院,北京 101416)

0 概述

卫星区域覆盖分析广泛应用于卫星任务规划[1]、成像侦察[2]等航天任务中。卫星区域覆盖分析指标[3]包括覆盖重数、面积覆盖百分比、覆盖累积面积、时间覆盖百分比、最大重访时间及平均重访时间等,其中面积覆盖百分比(覆盖率)在很多应用中是核心指标。

卫星区域覆盖分析方法主要包括解析法、基于几何运算的方法和网格点法。解析法[4]基于卫星与地球的几何关系直接得到覆盖面积计算的解析公式,只适用于单颗卫星且目标区域包含卫星覆盖范围的情况。基于几何运算的方法[5-7]在经纬度平面上利用多边形布尔运算计算覆盖指标,其中,文献[5]算法只适用于卫星瞬时覆盖,文献[6]算法的通用性和效率更高。卫星区域覆盖分析的经典算法是数值仿真的网格点法[8],该方法实现简单,但计算量大、空间复杂度高、计算结果精度受网格大小影响,文献[9-10]均直接采用网格点法。为提高网格点法的效率,研究者对原始的网格点法进行改进,其中,文献[11]利用网格点的空间相关性和边界特征,提出“池中投石法”“油环点火法”和“逐步吸收法”3种优化技术,文献[12]对网格点的卫星覆盖时刻集进行优化,文献[13]提出经度条带法,对每个条带应用解析方法。

网格点法的效率瓶颈为卫星采样点与网格点覆盖关系计算次数多,且网格点信息记录次数多。针对以上问题,本文算法通过扫描线与覆盖带多边形求交,将逐采样点、网格点计算优化为一次处理一个覆盖条带和一行网格点,并把扫描线划分为具有相同覆盖属性的分段,省略了网格点信息记录过程。

1 基于网格点的扫描线构造与数据维护

1.1 网格点法原理

网格点法的基本原理是:在经纬度平面上根据目标区域的包围盒划分网格,有等经纬度网格和等面积网格2种划分策略[14],以网格中心点代表网格进行计算;按给定步长计算卫星采样点,计算并记录卫星采样点对网格点的覆盖情况;通过统计网格点覆盖信息得到覆盖指标,如覆盖网格点数除以总网格点数得到覆盖率。

算法需判断每个卫星采样点与网格点的位置关系,同时记录每个网格点的覆盖信息,因此时空复杂度均较高。

1.2 扫描线及其数据结构

扫描线是计算机图形学中的经典技术[15],其基于目标区域的剖分网格定义扫描线,并利用扫描线实现卫星区域覆盖指标的快速计算。

如图1(a)所示,目标区域按等面积原则进行网格划分(实际空间大小接近,经纬度平面不均匀,纬度越高,网格越大),其中A、a、b等圆点为网格中心点。每行内各网格大小相同,网格中心点纬度值相同,构成水平扫描线,如图1(a)中1、2、3所指示的水平线。

扫描线划分为互不重叠的段,如图1(a)中扫描线2分为ab、cd、ef3个段。段数据结构定义为:

struct Seg{

int x0,x1;

vector satellites;

vector times;}

其中包括几何和覆盖属性2类信息。以端点表示段几何信息,端点采用整型数据类型,以避免导致过细的段划分。覆盖属性包括覆盖卫星及覆盖时间,每个段的覆盖属性一致,可有多卫星覆盖段或同一卫星多次覆盖段。

每条扫描线由不重叠且坐标值由小到大的有序Seg数组构成,所有扫描线数据再组织为数组。如图1(b)所示,目标区域在纬度被划分为100行,采用100个元素的数组存储。其中扫描线50共有200个网格点,被分为3段,网格点50～80被Sat0覆盖,网格点110～130同时被Sat0和Sat1覆盖,网格点150～170被Sat1在不同时间进行2次覆盖。

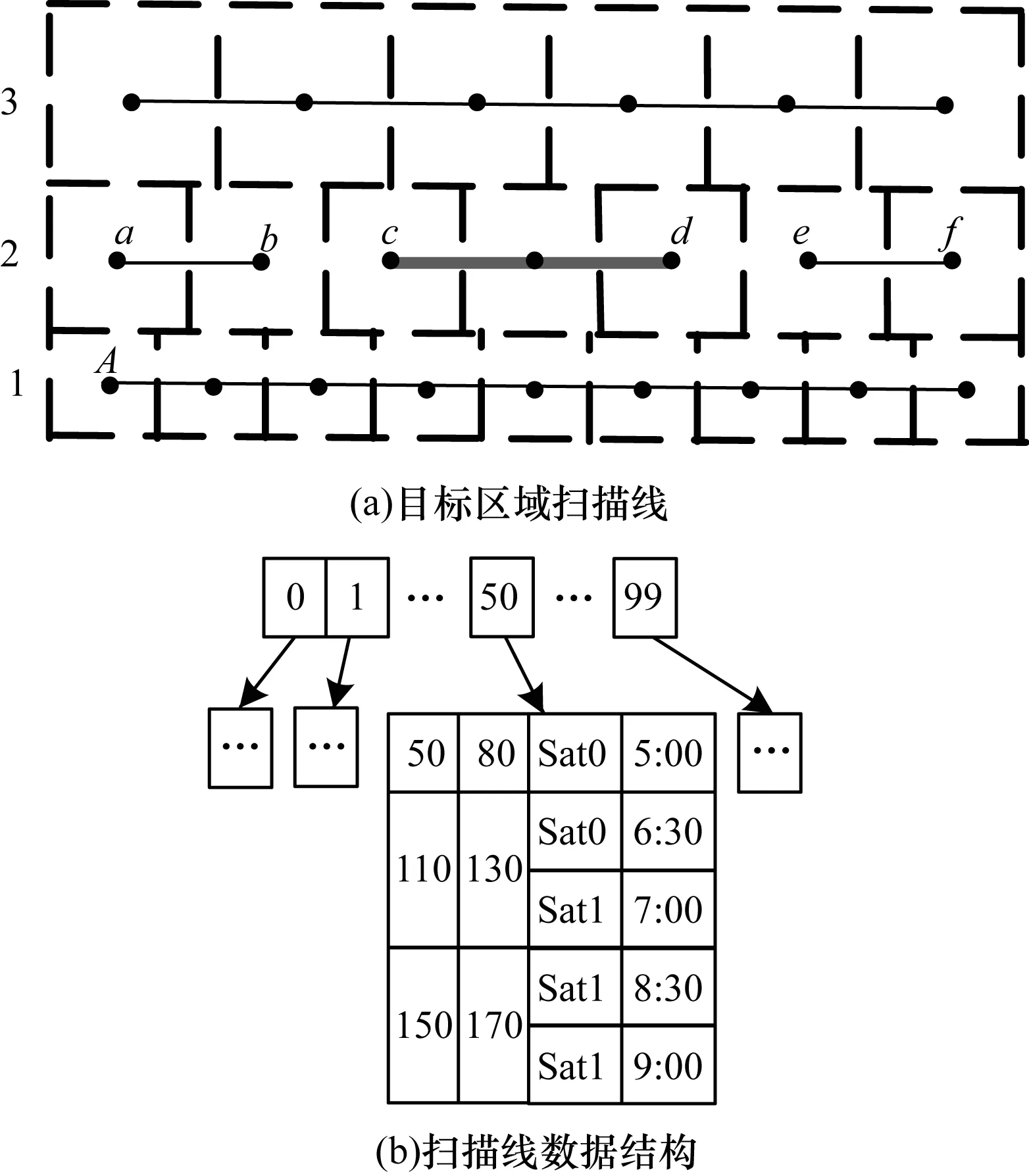
图1 目标区域网格的扫描线及其数据结构Fig.1 Scanline of the target area grid and its data structure

1.3 扫描线数据维护方法

扫描线段数组初始为空,计算过程中不断插入新段,插入过程需保持数组中段不重叠、有序。

在插入新段时,按序判断与原有各段关系并进行处理,如图2所示,新插入段cd与已有段ab有5种位置关系:1)cd全部位于ab左侧,将cd插入到段数组ab之前;2)cd部分位于ab左侧、部分位于ab之间,从数组中删除ab段,将ca段(覆盖属性同cd)、ad段(覆盖属性为ab合并cd)、db段(覆盖属性同ab)插入数组;3)cd全部位于ab之间,从数组中删除ab段,将ac段(覆盖属性同ab)、cd段(覆盖属性为ab合并cd)、db段(覆盖属性同ab)插入数组;4)cd部分位于ab之间、部分位于ab右侧,从数组中删除ab段,将ac段(覆盖属性同ab)、cb段(覆盖属性为ab合并cd)插入数组,构造bd段(覆盖属性同cd),继续将其与数组中后续段进行处理;5)cd全部位于ab右侧,继续将其与数组中后续段进行处理。在上述过程中,需避免段之间重叠,如假设第2)种情况a点坐标为10,则形成的新段范围为(c,9)、(10,d)。

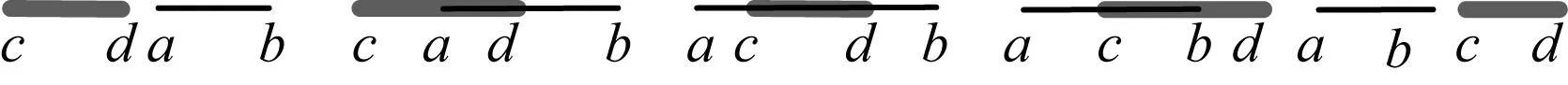
图2 待插入段与已有段的位置关系
Fig.2Relationships between positions of the segment to be inserted and the existing segment

2 卫星区域覆盖分析算法

本文算法步骤具体如下:

步骤1计算目标区域包围盒并进行网格划分,得到各扫描线纬度值和经度范围。如图3所示,目标区域为ABCDEFG,根据其包围盒进行网格划分。

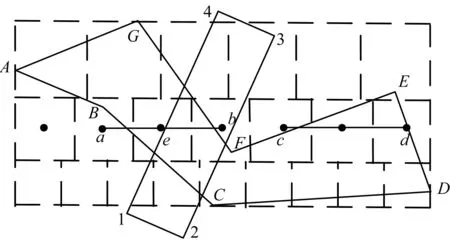
图3 卫星区域覆盖分析算法原理Fig.3 Principle of the statellite regional coverage analysis algorithm

步骤2扫描线与目标区域求交,相交部分作为初始计算对象,参与后续计算。在图3中,第2条扫描线与区域求交结果为ab、cd,将其作为初始计算对象。

步骤3计算卫星覆盖在经纬度平面的投影,得到覆盖带多边形,如图3中多边形1234所示。

步骤4对于每条扫描线,计算所有覆盖带多边形与初始计算对象的交,并根据卫星信息构造段数据结构,插入扫描线段数组中。在图3中,ab与覆盖带相交结果为eb,根据卫星信息构造Seg数据结构,插入第2行扫描线的段数组中。

步骤5遍历所有扫描线的所有段,统计满足条件的覆盖网格数。在图3中,如eb段满足统计条件,覆盖网格数为b-e+1。在计算总覆盖率时,所有段均满足要求,以网格点数除以总网格点数得到总覆盖率。

在本文算法中,以段代表其上所有网格点,几何运算本身决定了段与其网格点具有相同的覆盖关系,与直接计算网格点相比不会发生错判。

3 算法实现中的关键技术

3.1 覆盖带多边形生成

根据上文算法步骤生成目标区域过境时间范围内的覆盖带多边形。每个卫星采样点对应2个覆盖带边界点,计算卫星采样点位置和覆盖角所确定射线与地球表面的交点,根据交点坐标计算经纬度。在图4中,A、a、B、b等点为覆盖带边界点。

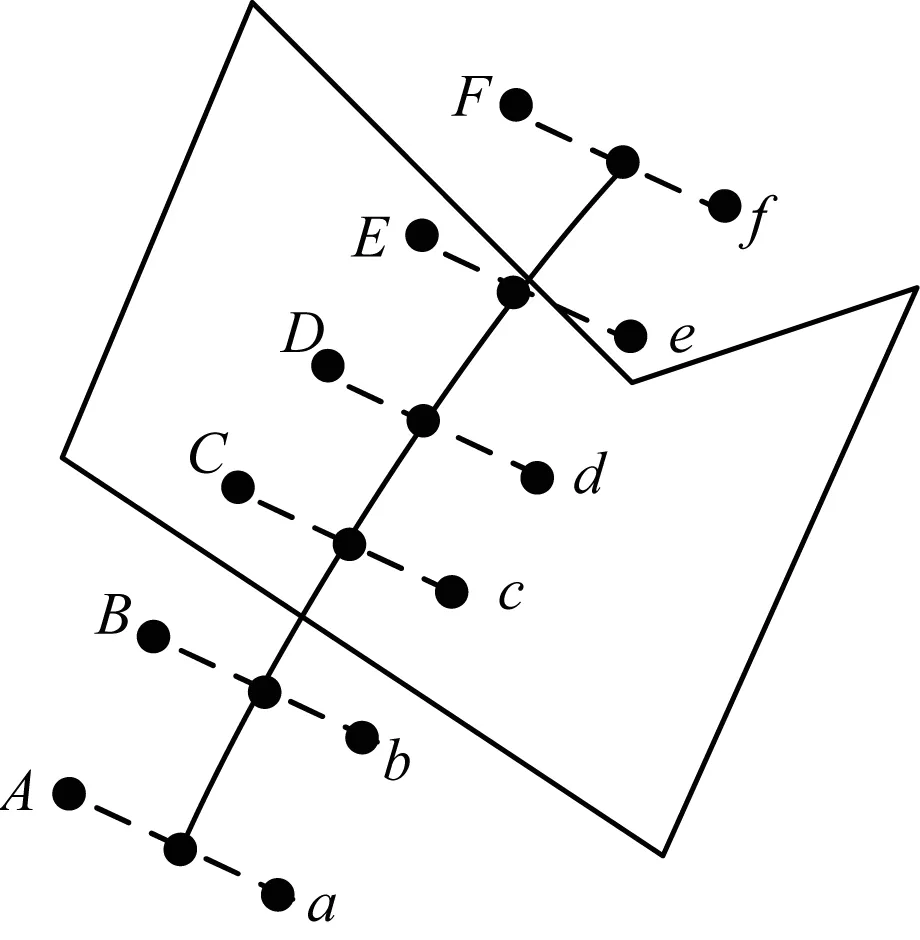
图4 覆盖带多边形生成过程Fig.4 Generation process of coverage band polygons

覆盖带多边形生成算法的伪代码具体如下:

generateCoveragePolygon{

for(每个卫星采样点){

if(采样点连线与目标区域有交){

if(无已构造覆盖多边形){

构造点表lpts和rpts;

并将前一组边界点输出到点表中;}

将边界点分别输出到两点表中;}

else if(点表不空){

边界点输出到两点表,

合并两点表为多边形并输出;}}}

在图4中,Aa、Bb与目标区域无交,不必处理;Cc与目标区域有交,需将BC输出到点表lpts中,bc输出到点表rpts中;依次处理,将DE加入到lpts,de加入到rpts中;Ff不再与目标区域相交,将Ff分别输出到两点表,此时lpts中为BCDEF,rpts中为bcdef,合并点表,得到覆盖带多边形bcdefFEDCB。

3.2 扫描线与多边形求交

在本文算法中,扫描线需与目标区域多边形和覆盖带多边形求交,具体步骤如下:

步骤1计算扫描线所在水平直线与多边形的所有交点并排序。如图5所示,对应扫描线AB到KM的交点集合分别为{1,2,3,4},{5,6},{7,8},{9,10},{11,12},{13,14}。

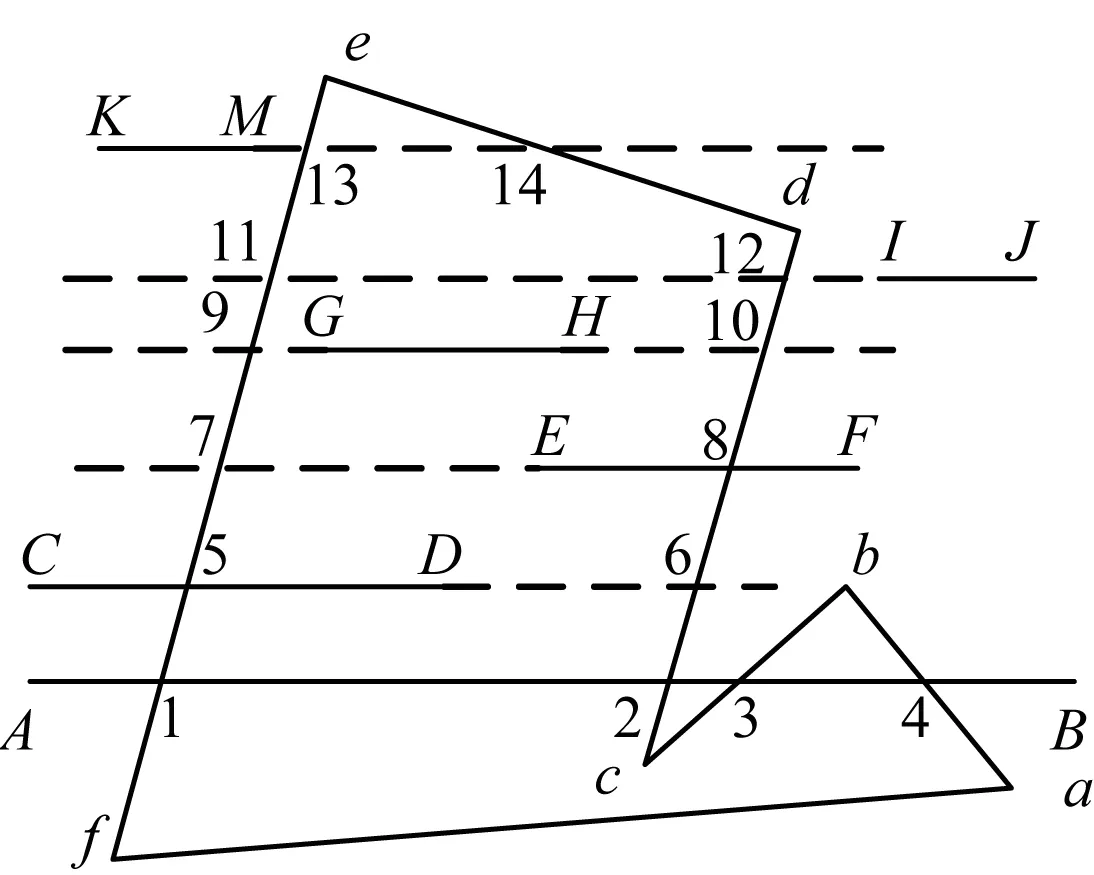
图5 扫描线与多边形的求交过程Fig.5 Intersection process of scanlines and polygons

步骤2处理扫描线起点。若起点位于所有交点右侧,则清空交点集合,转步骤4,如图5中的扫描线IJ;若起点位于所有交点左侧,则转步骤3,如图5中的扫描线AB、CD、KM;否则,将起点插入到交点数组,并删除起点左侧所有交点,如图5中的扫描线GH交点集合变为{G,10}。此时,交点集合变为{1,2,3,4},{5,6},{E,8},{G,10},{ },{13,14}。

步骤3处理扫描线终点。若终点位于所有交点左侧,则清空交点集合,转步骤4,如图5中的扫描线KM;若终点位于所有交点右侧,则转步骤4,如图5中的扫描线AB;否则,将终点插入到交点数组,并删除终点右侧所有交点,如图5中的扫描线GH交点集合变为{G,H}。此时,交点集合变为{1,2,3,4},{5,D},{E,8},{G,H},{ }。

步骤4交点数组中每2个交点形成一个输出段,图5中输出段为12、34、5D、E8、GH。

4 算法精度、效率及算例分析

4.1 算法精度分析

网格点法以网格点代表目标区域,计算结果存在误差,精度取决于网格大小(网格点距离)和卫星采样频率,网格点和卫星采样点越密,精度越高。

多星区域覆盖分析计算本身无解析解,现有研究大多以网格点法随网格缩小所逼近的值作为分析依据,如将每千米的经线数作为计算精度,其实质仍是网格越密,精度越高。

本文算法以段代表包含的网格点,对于每个网格点的判断与网格点法一致,因此精度与网格点法一致,影响因素是扫描线间距(扫描线基于网格点定义,间距与网格点密度一致)和卫星采样点密度。

4.2 算法效率分析

本文算法通过覆盖带多边形过滤未过境卫星采样点,传统网格点法也可通过其他技术进行过滤,因此假定2种算法都仅能计算过境时间范围采样点。

设卫星过境次数为k,过境采样点数与步长、区域大小等有关,设为常数c。目标区域网格数设为m行n列。

在传统网格点法中,采样点与网格点覆盖关系判断时间复杂度为O(ckmn),网格点信息记录时间复杂度也为O(ckmn)(每个网格点需多次记录信息)。每个网格点都需记录信息,因此空间复杂度为O(mn)。

本文算法扫描线与覆盖多边形相交计算时间复杂度为O(km),如基于覆盖多边形顶点数分析的时间复杂度为O(ckm),但此时基本计算是坐标比较,效率远高于网格点法中的覆盖判断。扫描线处理过程中需插入新段,段数最大与过境次数相等,因此插入新段的时间复杂度为O(k),一行扫描线处理段的时间复杂度为O(k2),全部扫描线处理段的时间复杂度为O(mk2)。因此,总的时间复杂度为O(ckm)+O(mk2)。一般应用中k值远小于n,O(ckm)+O(mk2)远优于网格点法的O(ckmn)。由于扫描线采用整型数据类型定义段,在极端情况k>n时,段数不超过n,此时算法时间复杂度为O(ckm)+O(mkn),效率仍远优于网格点法。本文算法空间复杂度取决于段的数量,为O(mk),但k>n时算法空间复杂度会限制在O(mn)内。

4.3 算例分析

通过网格点法[8]、文献[12]算法和本文算法对2个算例进行覆盖分析:算例1，目标区域为凹多边形，跨度约为20°，包含8颗卫星、过境22次；算例2，目标区域为凹多边形，跨度为3°，包含12颗卫星、过境29次。算例1和算例2的耗时如表1、表2所示。由此可知,本文算法效率高于网格点法,网格数越多,效率提升越明显,在网格数量超过80万时,耗时仅为网格点法的1.19%。

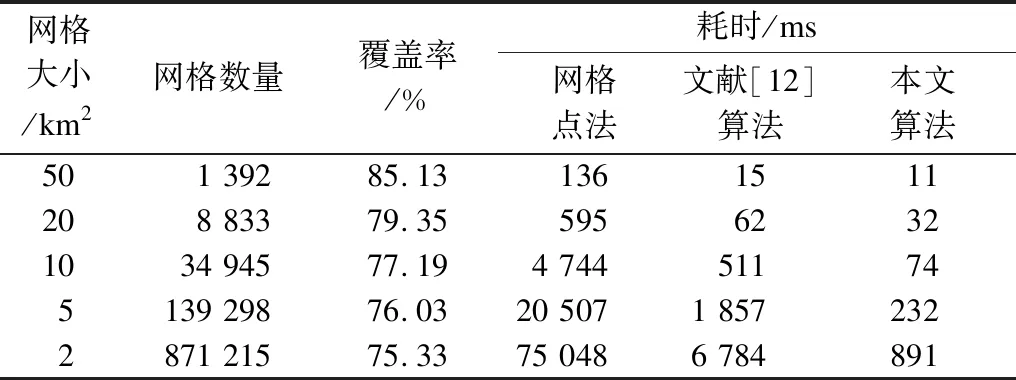
表1 算例1耗时对比Table 1 Comparison of consumed time in Example 1

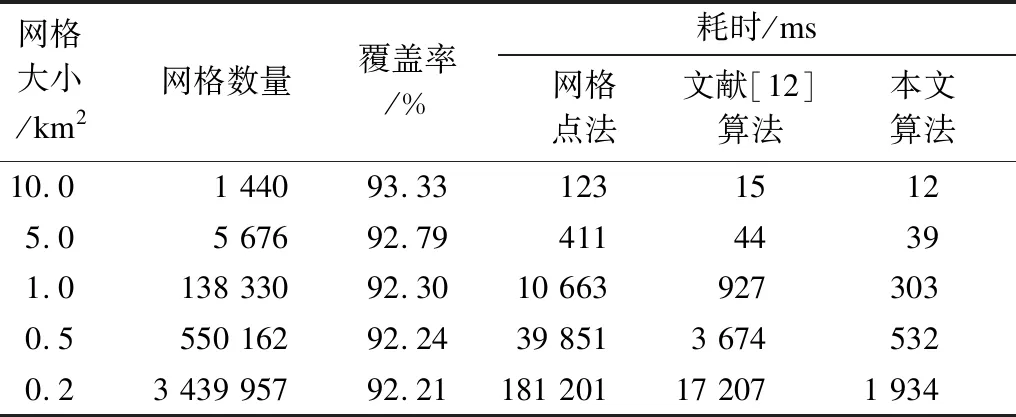
表2 算例2耗时对比Table 2 Comparison of consumed time in Example 2

5 结束语

本文利用网格点的空间相关性,基于扫描线思想实现覆盖带多边形生成、扫描线与多边形求交等关键技术,完成网格覆盖计算的批量处理。算例分析结果表明,本文算法的时间复杂度和空间复杂度均优于传统网格点法,尤其适用于大范围非规则目标区域的高精度卫星覆盖指标计算。下一步将在提高卫星区域覆盖分析效率的同时,对时间覆盖百分比、最大重访时间等相关指标的计算问题进行研究。