基于随机矩阵理论的WSN异常节点定位算法

林 超,郑 霖,张文辉,邓小芳

(桂林电子科技大学 a.广西无线宽带通信与信号处理重点实验室; b.广西云计算与大数据协同创新中心;c.广西高校云计算与复杂系统重点实验室,广西 桂林 541004)

0 概述

物联网(Internet of Things,IoT)被广泛应用于环境监测、智能交通、工业控制、医疗系统、海洋农业等领域[1],作为其核心技术之一的无线传感器网络(Wireless Sensor Network,WSN),是由大量具备感知、数据处理、数据存储和通信等功能的微型节点组成的自组织网络[2],通过分析其采集的区域数据信息可以达到实时监控该区域的目的。然而,在采集的海量数据中存在显著偏离于正常感测数据的异常值,这些异常值产生的原因有很多,如某些节点发生故障(能量耗尽、受到外界攻击等),或是发生了异常事件(如森林火灾、交通拥塞等),同时,正常数据也会在一定范围内发生合理的波动。因此,异常事件检测是WSN中关键技术之一,可及时发现隐藏在海量数据中的异常数据或异常状态,帮助决策者直观迅速地了解网络当前运行情况,做出正确的判断和决策,从而及时解决异常问题[3]。

通过对网络波动数据进行异常检测,可以有效地发现异常情况并定位异常节点,在WSN实际应用中具有重要意义[4]。目前对实时高效、准确的WSN异常事件检测算法的研究逐渐深入,在所有异常检测的算法中,基于经典统计学的方法需要假设采集的数据符合一个统计模型[5],然后通过评估数据和模型的匹配度来确定未知数据是正常数据还是异常数据。该方法在异常检测中有着较高的准确率,但也存在明显的缺点,即必须已知数据所满足的特定统计模型,而在实际的应用当中,网络数据统计模型往往很难事先获得或精确描述。

异常检测还会采用基于临近点的检测方法[4-5],该方法通过计算数据集中每个数据之间的相似度(距离)对异常点进行识别,一种典型的基于临近点方法的异常检测算法是LOF(Local Outlier Factor),该算法可以有效识别异常,但存在2个不足:首先是其计算复杂度高,海量数据下的计算开销不可忽视;其次是虽然LOF算法可以有效地发现孤立异常对象,但如果出现异常对象聚集在一起的情况,LOF算法的异常检测准确率将大幅下降。此外,常用的异常检测方法还有分类方法[6]和聚类分析法[7]等。

近年来,已有学者开始将数理统计学中的随机矩阵理论(Random Matrix Theory,RMT)应用到通信领域。文献[8]针对经典特征值类频谱感知算法在低采样、低信噪比下检测效果不佳的问题,提出一种基于随机矩阵特征值差的频谱感知改进算法。文献[9-10]阐述了随机矩阵理论与无线通信紧密的联系和数学背景,展示了随机矩阵理论处理无线通信领域问题的优势。文献[11]将随机矩阵理论中的单环定律应用于频谱感知的研究中,设计了基于单环定律的频谱感知算法。文献[12]使用随机矩阵理论作为大数据分析的框架并将其应用于移动蜂窝网络中的数据分析。相比传统的数据分析方法,随机矩阵理论能够在一定程度上摆脱传统的物理模型,充分利用数据资源,从数据驱动角度分析挖掘网络的关联性和运行特征。研究者通过利用随机矩阵理论中一些优良、成熟的定理和特性,从高维的视角分析并解决通信系统中存在的问题,取得了一定的效果。

为对WSN高维数据进行实时有效的分析，检测网络中是否出现异常并定位异常节点的位置，本文基于随机矩阵理论设计一种WSN异常节点定位算法。

1 随机矩阵理论

随机矩阵是一个以随机变量为元素的矩阵,其概念由WIGNER等人提出并吸引了许多数学家和统计学家对其进行深入研究,逐渐形成了随机矩阵理论。经验谱分布是随机矩阵理论中的一个重要概念,对于一个特征值均为实数的n×n维随机矩阵A,称以下分布函数为该矩阵的经验谱分布(Empirical Spectrun Distribution,ESD):

(1)

其中,λi(i=1,2,…,N)为特征值,I{·}表示指示函数。当随机矩阵A的行数和列数趋于无穷大且行列比保持恒定时,其经验谱分布函数将收敛到一个非随机的函数,称为极限谱分布(Limit Spectral Distribution,LSD)函数。此时,许多优良的性质将会表现出来,如Marchenko-Pastur律(M-P律)、平均谱半径(Mean Spectral Radius,MSR)、单环定理、半圆律[13]。本文研究主要采用单环定理和平均谱半径。

1.1 单环定理

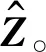
(2)

其中,c∈(0,1],c为常数。在复平面上,矩阵Z的特征值大致分布在一个内径为(1-c)L/2、外径为1的圆环内。

1.2 平均谱半径

利用平均谱半径可以从高维视角描述系统的统计特征[15]。由随机矩阵理论可知,当系统中有异常事件(异常的信号源)发生时,其统计随机特性将会被破坏,随机矩阵的特征值分布会发生变化,rMSR可反映随机矩阵的统计特性故将其作为评价指标。平均谱半径计算公式如下:

(3)

其中,λi(i=1,2,…,N)为协方差矩阵的特征值。

2 网络异常情况分析与异常节点定位

在进行网络异常分析和异常节点的定位之前,首先要明确异常值的定义,本文采用文献[16]中的异常值定义:异常值是指在数据集中偏离正常数据模型的数据,其是由完全不同的机制产生而不是由随机误差导致。根据此定义,本文将与正常数据模型不一致的数据判定为异常数据。

在WSN中,正常情况下采集到的数据符合独立同分布,而一旦出现异常情况,数据将不再满足独立同分布。随机矩阵理论作为对高维数据进行统计分析的方法之一,可从高维的视角判断WSN采集的数据中是否有异常数据出现。因此,本文基于随机矩阵理论,从整体上分析网络是否出现异常,并在此基础上利用最大特征值对应特征向量的最大元素定位法对出现异常的节点进行定位。

2.1 基于随机矩阵理论的网络异常态势分析

由于WSN采集的数据具有独立的时空特性,因此本文首先利用数据的时空特性对原始数据进行组织以及数据的归一化和标准化预处理。

假设节点数为N个,每个节点的采样总时间为T(T>>N),则N个节点的数据可用矩阵XN×T表示：

(4)

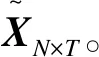
(5)

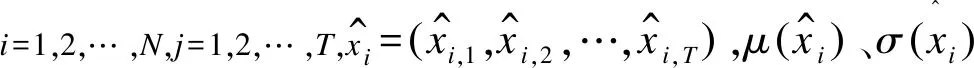
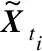
(6)

由单环定理计算每个采样时刻滑动窗内数据的特征值以及采用式(3)计算对应的平均谱半径,当窗口滑动结束后,可根据各个时刻平均谱半径的值绘制出趋势图并对其进行分析。当感测的数据处于正常模式时,其平均谱半径不会突变；当发生异常扰动时,在该异常发生的一段时间内,平均谱半径会发生显著的变化。因此,本文使用平均谱半径作为评价指标来判断网络整体态势。算法描述如下:

算法网络异常态势判断算法

输入数据矩阵X,窗口宽度Tw,总时间T

输出每个采样时刻平均谱半径值r(i)

for i=Tw:T

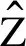
2.2 异常节点定位

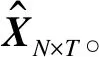
(7)

然后对协方差矩阵P进行特征值分解,可得:

(8)

Pvk=λkvk

(9)

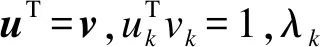
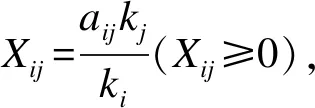
根据上述定理并结合式(9)可做如下推导:

(10)

(11)

由此可知,在第k个特征值λk对应的特征向量vk中,特征向量vk的第i个元素vki的变化只与矩阵P的第i行有关联,因此,当矩阵P的第i行出现异常波动时,将导致特征向量vk上第i个元素的值出现显著变化且与其他元素有明显的区别,即当第i个节点的感知数据出现较为明显的变化时,会在数据的处理中同时反映在其特征向量的第i个元素,相反地，vkj(j≠i)的其他元素则与P的第i行数据无关。利用这一关系,可以通过观察特征向量的元素进行异常位置的定位。由特征值分解的含义可知,特征值和特征向量可以清晰地反映出矩阵在哪些方面产生的效果最大,矩阵的特征值越大,反映出矩阵在该特征值对应的特征向量上产生的效果或者能量越大,因此，在仿真实验中依据特征值的大小,通常对前4个较大特征值对应的特征向量元素进行分析并判断出现异常情况概率最大的节点。

3 仿真结果与分析

本文异常节点分析仿真分为2个部分进行,仿真1针对网络的整体运行情况是否出现异常进行分析,仿真2则在仿真1的基础上进行网络中异常节点的定位。

3.1 实验数据来源

本文通过英特尔伯克利实验室(Intel Berkeley Research Lab,IBRL)实地部署的无线传感器网络采集到的数据进行实验[17-18]。IBRL网络由55个节点构成,整个网络在2004年2月28日—2004年5月5日之间,每隔30 s采集一次数据,每条数据包含温度、湿度、电压、光照强度以及时间标记5个属性。在实验中,本文选取50个传感器采集的电压数据,将3月6日00:00开始的共1 000个采样时刻的数据构成大小为50×1 000的原始数据矩阵,通过人工注入多种类型异常来验证该算法的有效性[20]。本文的异常数据集由4种异常类型组成,其分别模拟了异常情况下4种数据变化的趋势,如表1所示,其中,n为异常持续的时长。异常类型1模拟了节点感测到环境中发生缓慢但又有区别于正常情况下的变化(如煤气泄漏导致空气中有毒气体含量的缓慢上升),其将导致节点在短时间内所采集的数据在数值上缓慢上升。异常类型2模拟了环境中出现较为剧烈的变化(发生火灾而导致温度在短时间内快速上升),这将导致节点在短时间内所采集的数据在数值上迅速上升。异常类型3模拟了传感器节点感测到外界环境极端的变化(如人为异物的遮挡或异物入侵等)而导致其采集的数据在数值上发生一定程度的骤变。异常类型4表示数据为0,模拟了节点受到外界异常的干扰导致故障,无法正常工作。

表1 异常类型及参数

3.2 性能评价指标

实验从异常节点定位准确率和误警率来衡量本文算法。其中，异常节点定位准确率Pd的定义为:存在异常节点时,成功定位异常节点的次数与实验测试次数比值的百分数。异常节点定位误警率Pfa的定义为:不存在异常节点时,误判为有异常节点的次数与实验测试次数比值的百分数。

3.3 实验结果与分析

仿真1对原始数据中的第5个节点,在350～449的采样时间段内根据表1的异常类型分别注入异常,取时间窗口Tw=90,按2.1节的方法对该含有异常的数据集进行分析,可得到如图1所示的仿真结果。

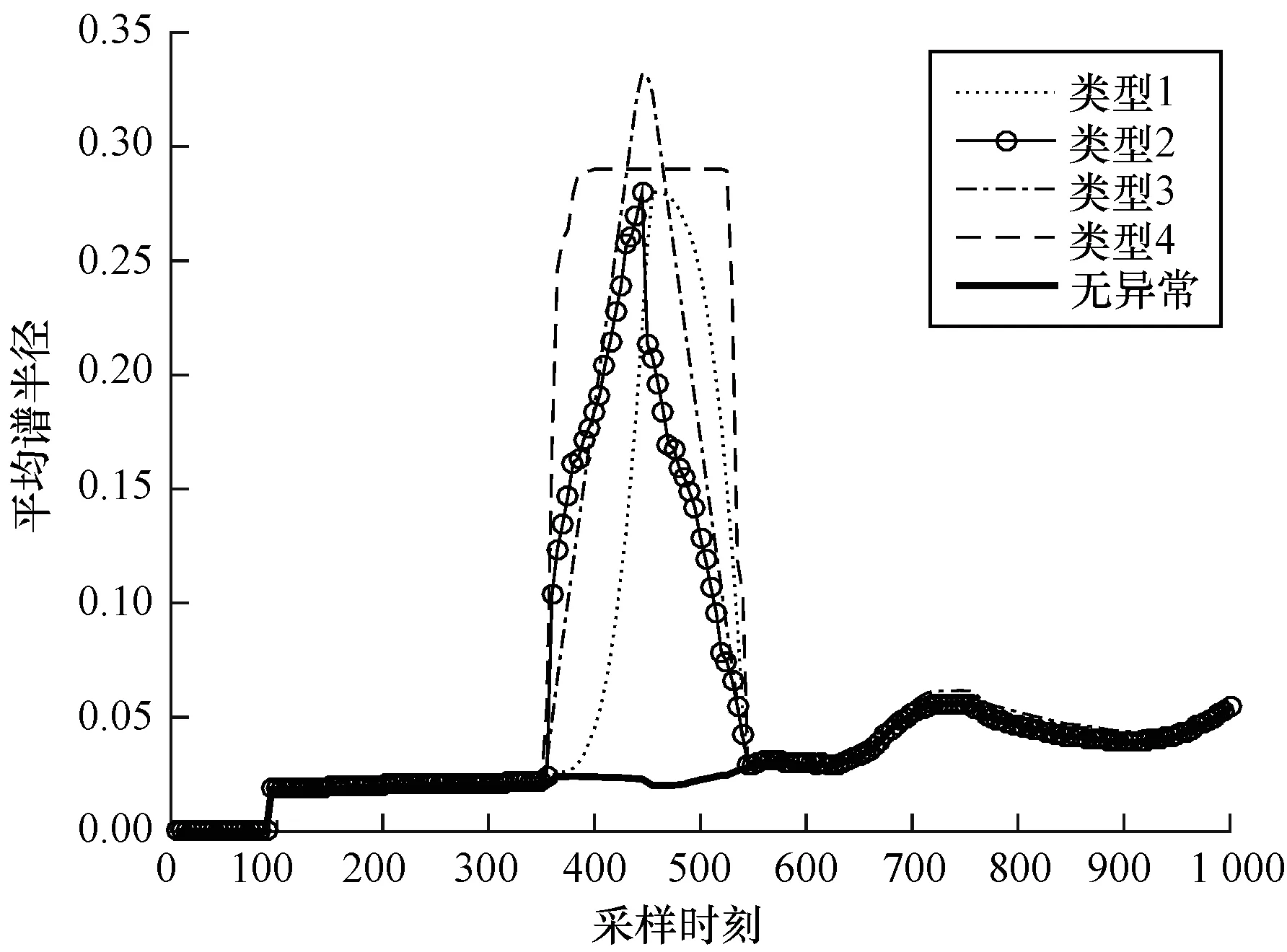
图1 4类异常情况和无异常情况下的平均谱半径Fig.1 MSR in normal condition and 4 abnormal conditions

由于时间窗口为90,因此从第90个采样点开始分析平均谱半径数值,通过与无异常情况下平均谱半径的曲线相比,注入的异常会造成平均谱的值显著增大,且不同的异常类型所导致的异常数据使得在异常发生时平均谱半径的趋势不同,由此可以分析出网络运行的整体态势,并检测出网络运行是否出现异常。

仿真2进一步分析定位数据异常的节点。首先对单个节点出现异常情况进行检测。针对第5个节点，在250～350时间段内人工注入类型1的异常数据(其他异常类型也可得到相同结论)。根据2.2节协方差矩阵特征值及对应特征向量(按特征值升序排列),检测矩阵中出现异常的行,以此对应到异常状态量。仿真结果如图2所示。

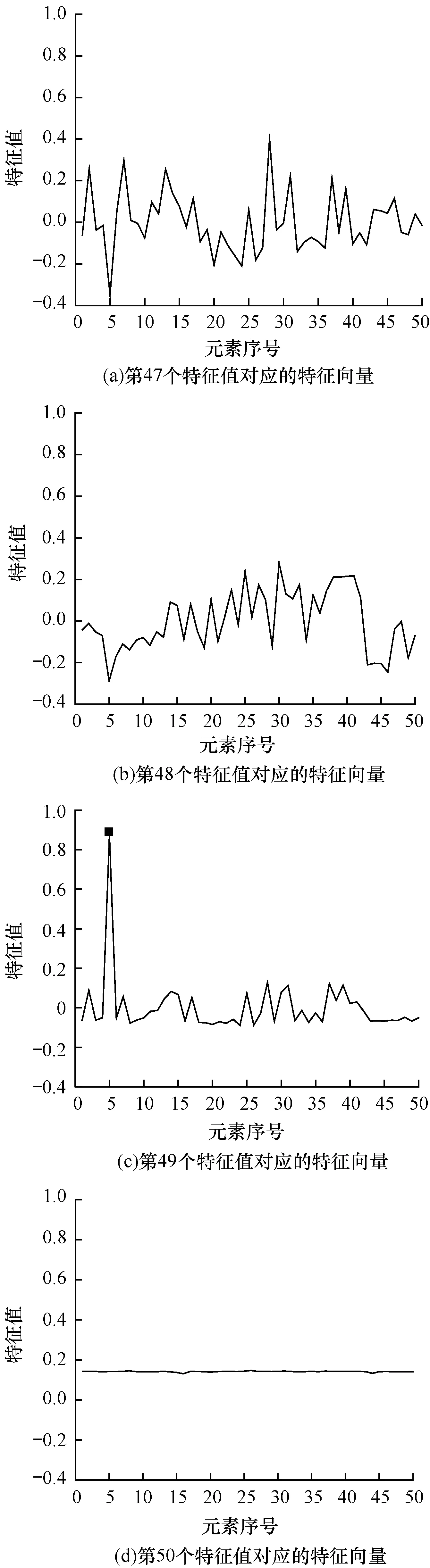
图2 单个异常节点情况下的特征向量元素分布

Fig.2 Distribution of eigenvector elements in presence of one single abnormal node

图2显示了前4个较大特征值对应特征向量元素的分布,通过比较可以看出,图2(c)具有较大的峰均比,而图2(a)、图2(b)和图2(d)均无此现象,与图2(c)形成明显的差异,图2(c)中在第5个特征向量元素处有明显的峰值,因此,判断第5个节点出现故障的概率最大。

为进一步验证本文算法的异常检测效果,本文选取了在WSN中典型的分布式故障检测(Distributed Fault Detection,DFD)算法[21]与本文算法在异常节点检测准确率上进行对比。对比实验中采用IBRL网络中1号～50号传感器节点在1 000个采样时刻内收集的温度数据,随机设置异常时刻和异常节点,使用2种算法分别对文中设计的4种异常类型各进行5 000次测试,所得异常节点定位准确率如图3所示。可以看出,DFD算法的异常节点定位准确率低于本文算法。

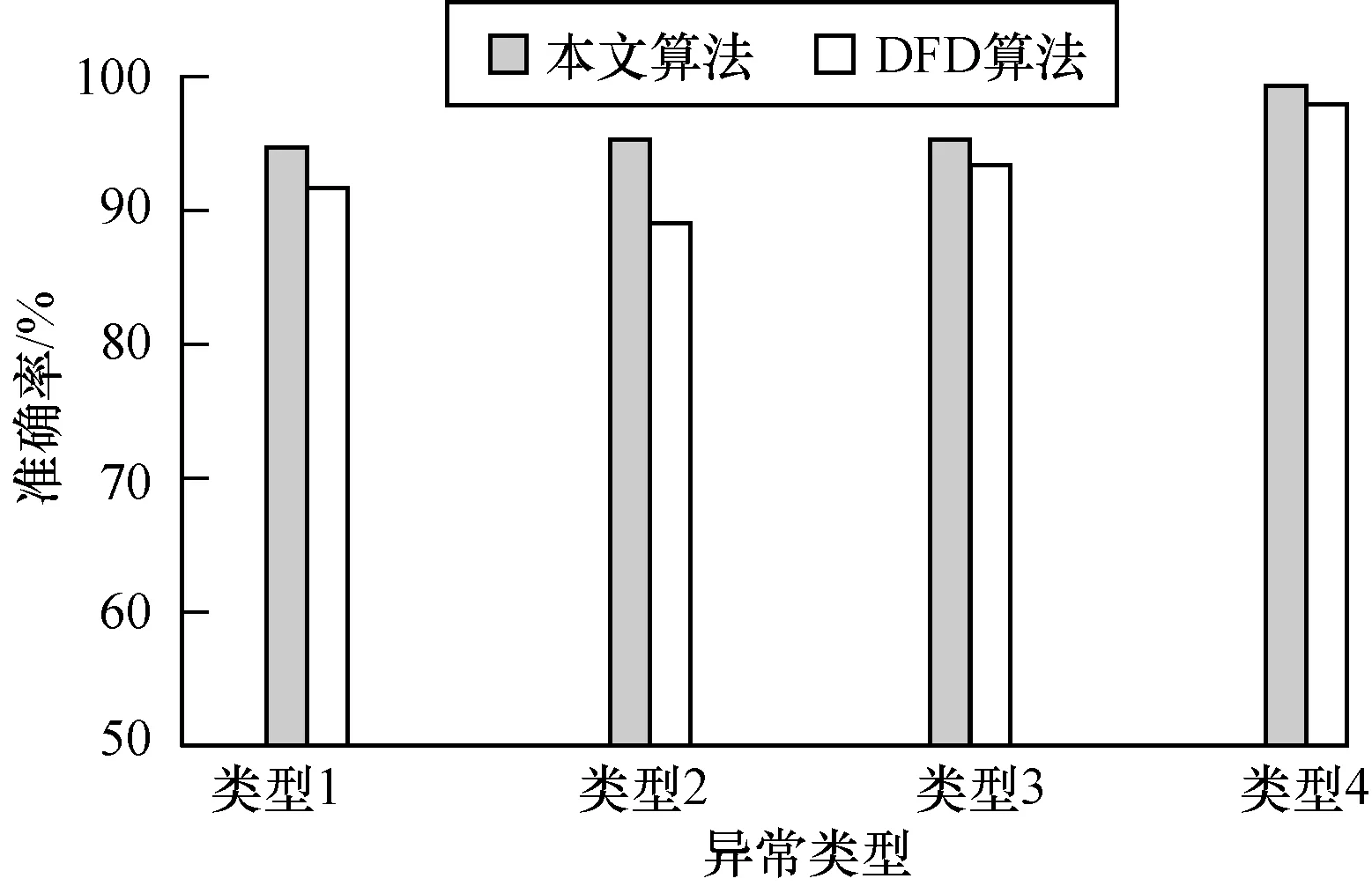
图3 单个异常节点定位准确率对比Fig.3 Location accuracy comparison of one abnormal node

此外,对多个节点出现异常情况进行定位。检测前对原始数据在550～650和250～350时间段内向第5个和第15个节点分别人工注入类型1和类型4这两种异常,根据2.2节方法进行检测,仿真结果如图4所示。可以看出,图4(b)和图4(c)在第5个元素和第15个元素分别出现了峰值点,且有较大的峰均比,而图4(a)和图4(d)中的峰均比都较小,由2.2节中的分析可知,第5个节点和第15个节点极有可能是异常节点。仿真结果与实验前人工注入的异常条件相符。

在多个异常节点的定位对比实验中,本文使用与之前对比实验同样的温度数据集,在所有节点中随机选取2个节点和2个时刻作为异常节点和发生异常的时间,依次选取异常类型表中类型1～类型4进行任意组合,共6种组合,使用本文的算法和分簇式DFD算法均进行5 000次的测试,并对比2个算法对多个异常节点定位的准确率,结果如图5所示。可以看出在本文所设计的算法在多个异常节点且存在多种异常类型的情况下,检测效果优于DFD算法。

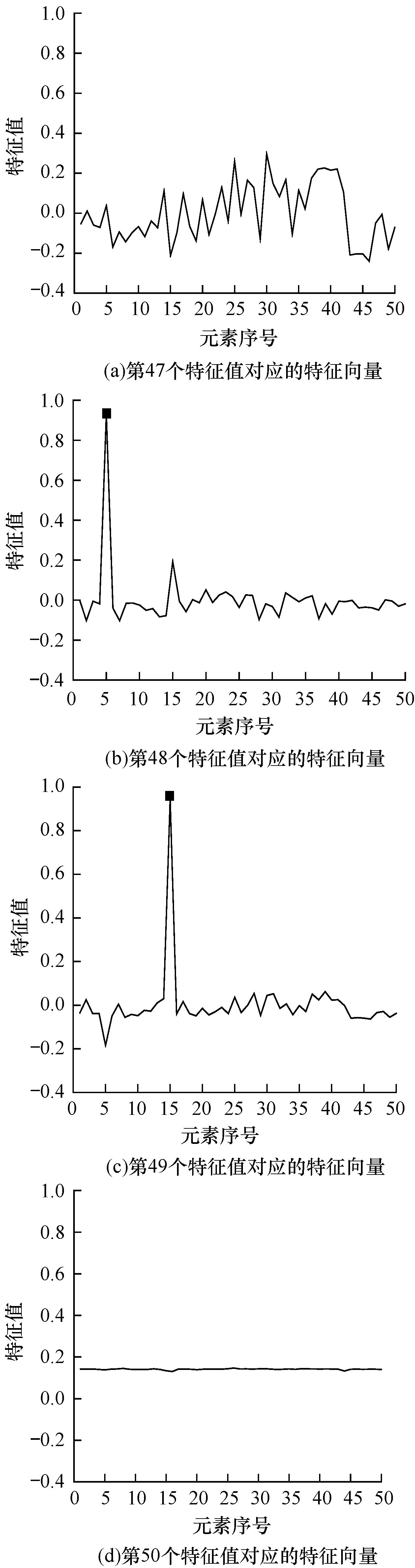
图4 多个异常节点情况下的特征向量元素分布

Fig.4 Distribution of eigenvector elements with multiple abnormal nodes

对本文算法和DFD算法的误警率进行对比,实验中不注入任何异常类型而只是存在普通噪声,结果如表2所示。仿真结果表明,本文设计的异常节点定位算法在异常节点的定位上性能优于经典的DFD算法,证明了本文算法的有效性与优越性。

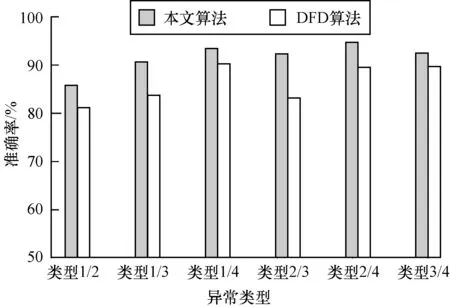
图5 2个异常节点定位准确率对比Fig.5 Location accuracy comparison of 2 abnormal nodes

表2 异常节点定位误警率对比

Table 2Experimental result comparison of abnormal node location%

算法误警率本文算法1.13DFD算法2.04

4 结束语

为从海量数据中快速有效地检测出异常情况并定位异常节点,本文设计一种基于随机矩阵理论的无线传感器异常节点定位算法。实验结果表明,在不同异常情况下，该算法均可以实时有效地检测出异常事件并定位异常节点，其检测性能优于DFD算法,在高维数据中具有较好的适用性。下一步将针对存在多类型节点和异构数据的复杂情况对本文算法进行优化。