理想气体状态变化中“变质量”问题的探讨①

(广东省中山市杨仙逸中学，广东 中山 528400)

1 问题的提出

2017年4月笔者曾在广东省中山市高考物理备考研讨会上作了一个分享，题为《对近六年全国高考”气体“考查特点的分析及2017年的备考策略》，着重探讨气体“变质量”问题，预测在以后的高考中会出现。

2 “气体”计算题的备考思路

(1) 要求学生对近年的高考全国卷的相关题目进行认真解答和研究，归纳类型，寻找规律，熟练把握，增强解决问题的信心。

(2) 认真研读课程标准和考试大纲，把握高考对高中物理各个模块考点的总体要求和变化，审视选考题的动向。

回顾2017年和2018年全国Ⅰ卷的气体考题，连续两年的考题类型比较接近，题型均属于双缸、双对象问题，这与2012年和2013年全国Ⅰ卷的考题相似，但是难度比之前有所下降。基于上述思考，笔者对理想气体状态变化中的“变质量”问题作进一步的分析和归纳，构建解决此类问题的基本模型，并通过具体的考题加以说明。

3 引入“气囊”模型，将“变质量”变为“定质量”

在实际问题中，变质量主要表现为充气和排气两种类型，在气缸充气或排气时，由于气体的质量发生改变，气体实验定律就不适用。为此，在充气或排气的变质量的问题中，笔者提出如下解题模型。

在给气缸充气时，设想用一气囊装着所需状态的气体，一次性经等温变化或等压变化到达末态；在气缸排气时，则用气囊装住经等温变化或等压变化排出的气体。这样就将“变质量”变为“定质量”，就能够利用气体定律解决问题了。

有教师会认为还有更好的办法，例如利用理想气体的状态方程亦可解决，在等温变化中可以利用关系式p1V1=p2V2+p3V3，当然，这的确是一个好办法，但是学生不一定能理解此关系式成立的缘由，也不一定是高考命题的本意，而且在有的问题中还不一定能用。

4 “气囊”模型的应用举例

4.1 等温充气或排气

例1(粤教版物理选修3-3)：一个自行车内胎的容积为2.0L，用打气筒给这个车胎打气，每打一次就把压强为1.0×105Pa的空气打进去125cm3，设打气前胎内没有空气，那么打了20次后胎内的压强有多大(设空气温度保持不变)？

解析：如图1所示，以打入车胎的全部气体为研究对象，打完后的状态作为末态。设想用一气囊装着所需状态的气体，一次性将气囊中的气体经等温变化达到末态。答案为1.25×105Pa。

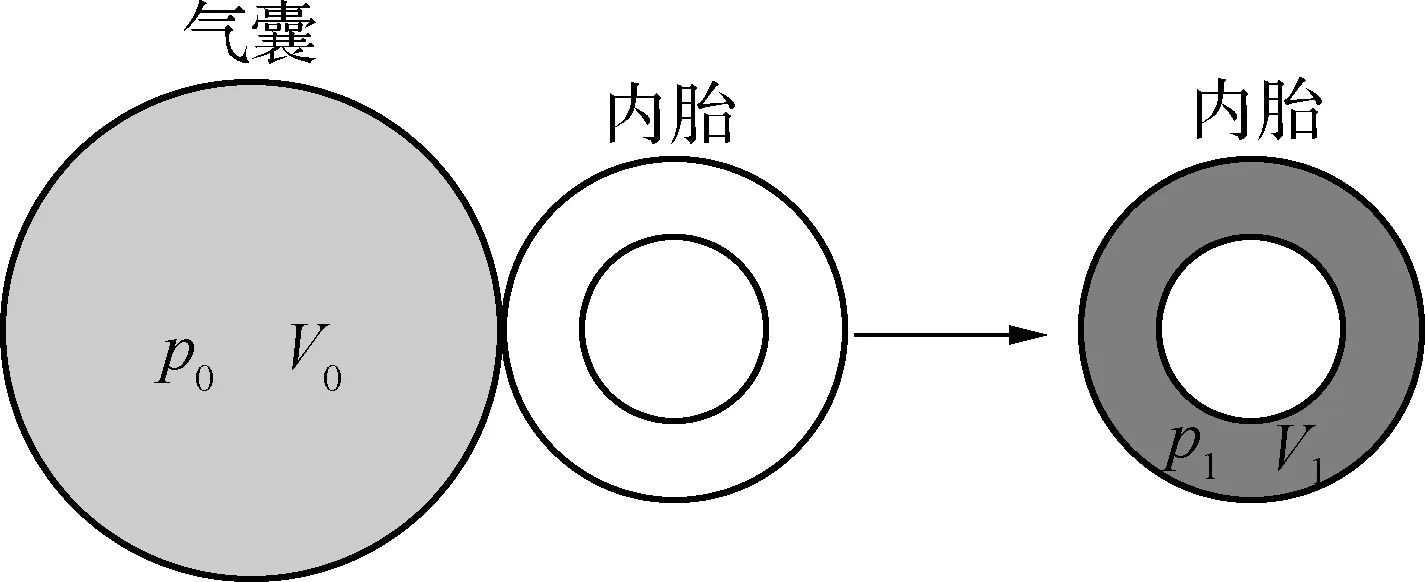
图1

追问：如果胎内原来有一定体积和压强的气体，那又该如何处理？考虑两种情况：(1) 若胎内原有气体压强与外界压强相同，则初态包括气缸内的气体和气囊中的气体；(2) 若胎内压强与外界压强不同，则先把胎内原来的气体先变化到初态(用第1个气囊装)，还需要的初态气体用第2个气囊装，再将两气囊的气体合并在一起，一次性地变到末态。

例2(2017年深圳二模)：如图2所示，质量m=2.0kg导热性能良好的薄壁圆筒倒扣在装满水的槽中，槽底有细的进气管，管口在水面上。筒内外的水相连通且水面高度相同，筒内封闭气体高为H=20cm。用打气筒缓慢充入压强为p0、体积为V0的气体后，圆筒恰好离开槽底。已知筒内横截面积S=400cm2，大气压强p0=1.0105Pa，水的密度水=1.0103kg/m3，g=10m/s2，筒所受浮力忽略不计。求：

(1) 圆筒刚要离开槽底时，筒内外水面高度差；

(2) 充入气体体积V0的大小。

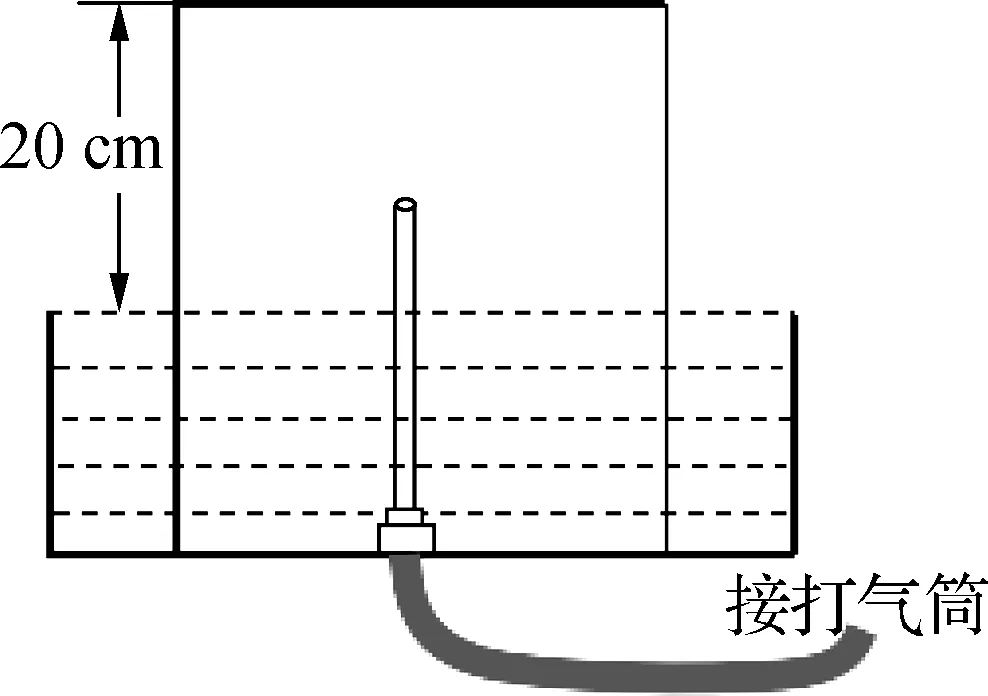
图2

解析：本题的处理方法与例1相同，答案为：(1)h=0.05m；(2)V0=2050cm3=2.05×10-3m3。

例3(2016年新课标Ⅱ卷)：一氧气瓶的容积为0.08m3，开始时瓶中氧气的压强为20个大气压。某实验室每天消耗1个大气压的氧气0.36m3。当氧气瓶中的压强降低到2个大气压时，需重新充气。若氧气的温度保持不变，求这瓶氧气重新充气前可供该实验室使用多少天。

解析：这是一道等温排气的问题，问题的难点在于如何理解“当氧气瓶中的压强降低到2个大气压时，需重新充气”，即还不能直接用，而且瓶内的剩余气体也用不上。为此我们采用“气囊”模型，分析3个状态。如图3所示，画出三个状态的示意图，问题即迎刃而解，答案为4天。

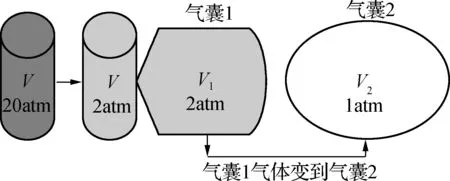
图3

例4(2019年新课标Ⅰ卷)：热等静压设备广泛用于材料加工中。该设备工作时，先在室温下把惰性气体用压缩机压入到一个预抽真空的炉腔中，然后炉腔升温，利用高温高气压环境对放入炉腔中的材料加工处理，改变其性能。一台热等静压设备的炉腔中某次放入固体材料后剩余的容积V=0.13m3，炉腔抽真空后，在室温下用压缩机将10瓶氩气压入到炉腔中。已知每瓶氩气的容积V0=3.2×10-2m3，使用前瓶中气体压强p0=1.5×107Pa，使用后瓶中剩余气体压强p1=2.0×106Pa，室温温度t1=27℃，氩气可视为理想气体。

(1) 求压入氩气后炉腔中气体在室温下的压强p2；

(2) 将压入氩气后的炉腔加热到1227℃，求此时炉腔中气体的压强p3。

解析：本题的处理方法与例3相同，解题思路如图4所示，答案为：(1) 3.2×107Pa；(2) 1.6×108Pa。

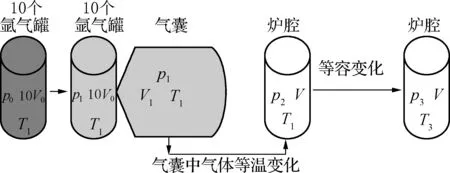
图4

4.2 等压排气(等压膨胀)

例5(2017年广州一模)：如图5所示，孔明灯的质量m=0.2kg、体积恒为V0=1m3，空气初温t0=27℃，大气压强p0=1.013×105Pa，该条件下空气密度ρ0=1.2kg/m3。重力加速度g=10m/s2。对灯内气体缓慢加热，直到灯刚能浮起时，求：

图5

(1) 灯内气体密度ρ；

(2) 灯内气体温度t。

解析：本题中变质量与力学平衡相综合，一定程度上增大了问题的难度。本题的排气是一个等压膨胀的过程，若采用“气囊”模型，化“变质量”为“等质量”，利用等质量的条件即可把密度和体积联系起来。先由力学平衡条件解出灯内气体的密度ρ，然后由等质量求等压膨胀后气体的体积V，即灯内气体的体积和用气囊所装的从灯内等压膨胀排出的体积之和，再由气体定律求解灯内气体温度T，解题思路如图6所示，答案为：(1)ρ=1.0kg/m3；(2)T=360K,即t=87℃。

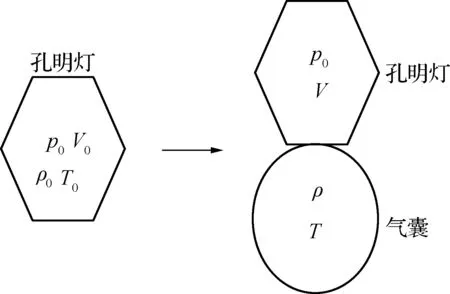
图6

5 结语

为解决变质量问题，引入了“气囊”模型，其实它也是一个理想模型，是一个想象中的物体，在现有的知识储备条件下，能有效帮助学生解决气体的变质量问题。在学习了理想气体的状态方程(克拉伯龙方程)以后，也可以用该方程解决变质量问题。