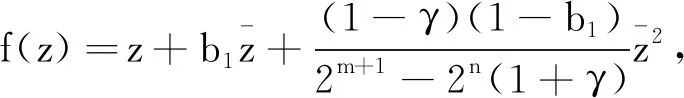单叶调和函数的一个子类

孙祚晨，王麒翰，龙波涌

(安徽大学 数学科学学院，安徽 合肥 230601)

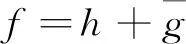
(1)

(2)

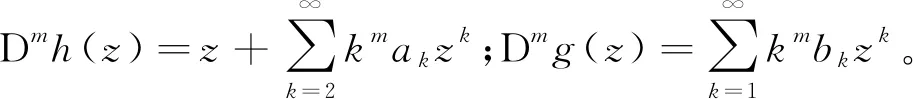
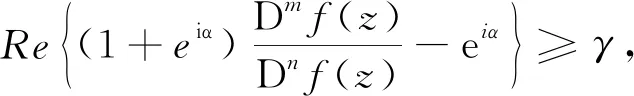
(3)

设

则f是单位圆盘U上的单叶保向调和函数，并且f∈GH(m,n,γ)。

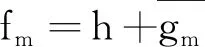
(4)

上是凸的。

设映射f：Ω→Ω′是同胚的，则f是一个K-拟共形映射当且仅当它满足如下2个条件：

①f在Ω内的线段上是绝对连续的；

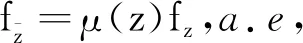
1 主要结果

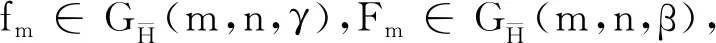
证明设

则由定理B，得

(5)

因此，

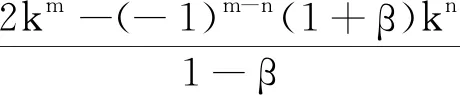
(6)

因γ、β∈[0,1)，当k≥2时，通过直接计算，得

[2km-(1+γ)kn][2km-(1+β)kn]-[2k2m-(1+γ+β-γβ)km+n]=
2k2m-(3+β+γ+γβ)km+n+(1+β)(1+γ)k2n=
k2n[2k2(m-n)-(2+(1+β)(1+γ))km-n+(1+β)(1+γ)]=
k2n(km-n-1)(2km-n-(1+β)(1+γ))≥0。

因此，若γ、β∈[0,1)，k≥2，则

[2km-(1+γ)kn][2km-(1+β)kn]≥2k2m-(1+β+γ-γβ)km+n。

(7)

更进一步地，当γ、β∈[0,1)时，对于k≥1，不管m-n是奇是偶，均有

[2km-(-1)m-n(1+γ)kn][2km-(-1)m-n(1+β)kn]≥
2k2m-(-1)m-n(1+γ+β-γβ)km+n。

(8)

根据式(5)～(8)，得

(9)

命题1设m∈N，n∈N0，m>n，则当γ、β∈[0,1)时，

(10)

据此，得

注1命题1说明定理1的结果改进了定理C的结论。

下面将通过定理2改进定理D的结论。

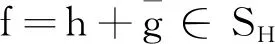
则f是凸的。

为证明定理2，需要在m∈N，n∈N0，m>n，γ∈[0,1)及k≥2的条件下建立一系列不等式。

若n≠0且m≥2，则

(11)

若n=1且m≥2，则

(12)

若n≥2，那么

(13)

因此，根据不等式(11)～(13)，当k≥2，n≠0且m≠1，m∈N，n∈N0时, 有

(14)

证毕。

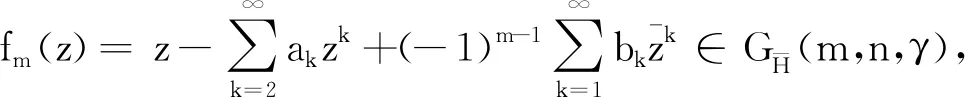
如果n=0，m≥1，k≥2，易得

从而,

(15)

若n≥1，k≥2，则

因此,

(16)

由式(15)、(16)，知

(17)

根据式(17)和定理B，得

因此，由b1+(1-b1)A<1得fm是K-拟共形映射。