基于FRFT 的多普勒频率跟踪算法

李静芳,丛 蔓,侯永飞

(1.中国电子科技集团公司第五十四研究所,河北 石家庄 050081;2.海军工程大学,湖北 武汉 430030)

0 引言

高动态环境下由于高机动用户运动等因素,造成用户接收卫星通信信号存在较大的多普勒频移,而相对运动加速度的存在会带来频率随时间的改变,造成多普勒频率变化率[1]。 在卫星通信系统中为了合理使用卫星转发器、提高用户容量,卫星通信信号通常采用高增益编码。 因此高机动用户终端需要在低信噪比条件下实现多普勒频移捕获及多普勒频率变化率的跟踪。 传统载波跟踪方法难以在高动态应力和跟踪精度两方面取得较好折中,针对这一问题提出了一种多普勒频率变化率快速估计方法,利用估计值辅助载波跟踪环路,并在信号设计中考虑插入分散导频用于跟踪载波,即可在低信噪比下完成载波剩余频率的跟踪,实现高机动用户多普勒频移捕获及多普勒频率变化率的跟踪。

基于分散导频的信号格式是将引导码间隔式分散地插入数据块当中,基于数据辅助的频率偏差估计归结为导频信号的频率估计问题和跟踪问题。 若在短时间内将加速度视为恒定,则载波信号等效于一个线性调频(Chirp)信号。 Chirp 信号最主要的性质是瞬时频率随时间呈线性变化。 分数阶傅里叶变换(FRFT)作为一个有效的Chirp 信号检测工具,可以应用到高动态接收机中,增加其抗噪声、抗多径干扰等能力,并能够更有效地跟踪到高动态信号[1]。 使用FRFT 可以同时对多普勒频率和多普勒频率变化率分量进行有效补偿,解决了传统FFT 在高动态环境下难以对高动态信号进行长时间相干累积的难题[2-3]。实现FRFT 传统方法一般都是基于相位增量计算或者是遍历搜索二维参量的方法进行估计。 相位增量法由于受限于相位估计的精度在低信噪比下精度急剧恶化,而二维搜索参量法需要消耗大量的时间,对于实时通信来说也不可行。 本文给出了一种滑动FFT 加FRFT 结合锁相环的频率和频率变化率估计的方法,在低信噪比下仍能保持较好的性能[4-6]。

1 多普勒频率变化模型

目前常用的高动态仿真模型有线性模型、正弦模型以及美国喷气推进实验室(JPL)定义的高动态模型。 线性模型较为简单,不能很好地描述飞机等平台的高动态特性。 仿真主要考虑正弦模型和JPL定义的高动态模型。

1.1 正弦模型

正弦模型将加速率自相关函数建模为余弦自相关函数为零的随机过程[7],能在一定程度上匹配高动态平台的多普勒频率及频率变化率特性：

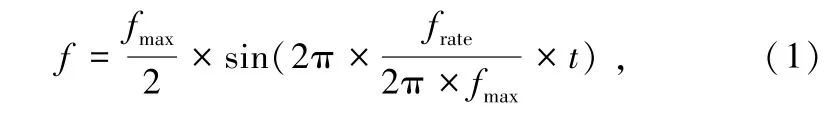
式中,fmax为最大频率偏移,frate为最大频率变化率,正弦模型加速度函数如图1 所示。

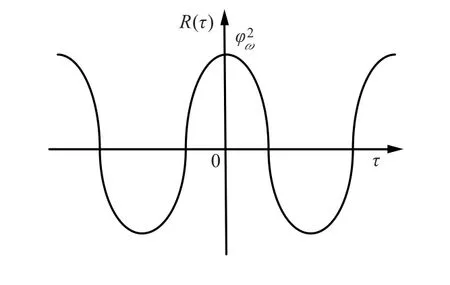
图1 正弦模型加速度函数Fig.1 Acceleratio n function of sine model

1.2 JPL 定义的高动态模型

JPL 定义的整个高动态过程的持续时间是8 s,其中最高动态发生在3 ～3.5 s,5.5 ～6 s,这2 个时段有100 g/s 的加加速度,其余时间是30 g 的常加速度运动。 高动态的速度、加速度、加加速度的变化轨迹如图2 所示。 可根据使用频率折算成多普勒频率、一次频率变化率及二次频率变化率[8-9]。

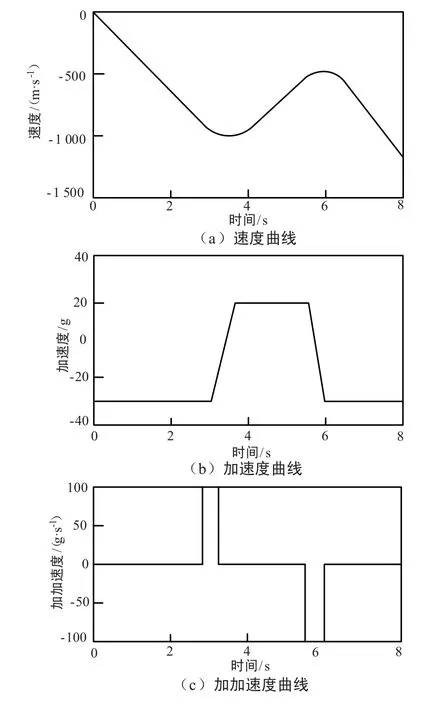
图2 JPL 高动态运动变化轨迹Fig.2 JPL high dynamic movment trochoid

2 多普勒频率跟踪原理

为了在低信噪比条件下完成载波频率跟踪,在信号设计时考虑加入分散导频。 基于分散导频的信号格式是将引导码间隔式分散地插入数据块当中,如图3 所示。

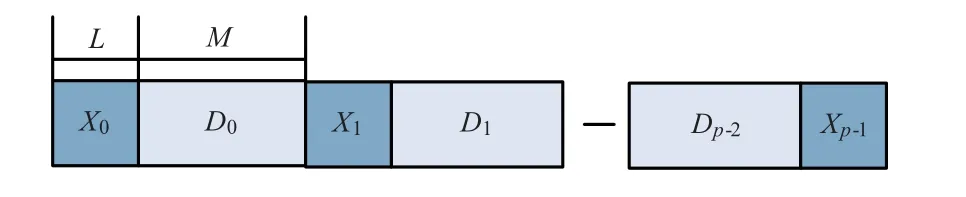
图3 分散导频信号帧结构Fig.3 Frame structure based on disperse pilot code signal

将PL 个引导码分成P 段,即X0,X1,…,Xp-1,每段长度为L 位,均匀插入数据块D0,D1,…,Dp-2中,数据块D0,D1,…,Dp-2每段长度为M 位[10]。 分散导频的优势在于：

① 分散导频是将引导码以固定间隔分散插入数据块当中,从参数估计角度来讲,通过拉长引导码间的距离增加了先验的时间信息[1];

② 引导码速率降低,提高了频率分辨率,如果采用相同长度的FFT,则谱线精度提高了,即谱线之间的分辨率提高了M 倍[10]。

③ 原来通过非线性变换提取载波的方法,可利用分散导频实现,这样可以保证在低信噪比的情况下,鉴频、相器输出仍然可靠。 基于分散导频的鉴频器输出如式(3)所示。

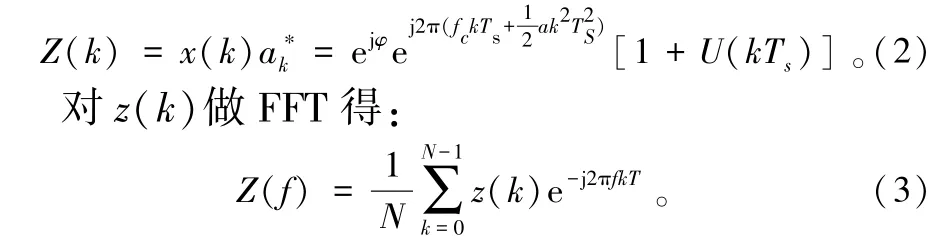
接收信号与导频数据共轭相乘后得到导频信号载波,通过FFT 变换后搜索周期图的峰值确定多普勒频偏,通过环路滤波器滤波后控制NCO,完成载波频率跟踪,原理框图如图4 所示。 当多普勒频率变化率较大,接近甚至超过符号速率时,周期图法提取的载波信号将出现严重的平台效应,同时导致FFT 运算后信噪比降低[11-12]。 为了扩大多普勒频率的跟踪范围,同时保证跟踪精度,采用基于FRFT的算法实现。

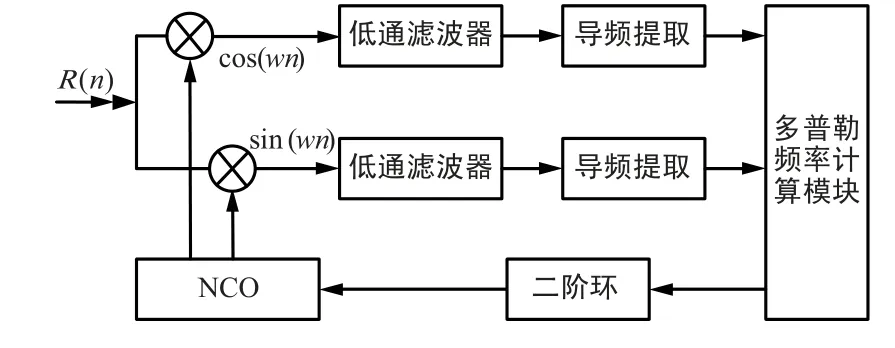
图4 多普勒频率跟踪原理图Fig.4 Dopler frequency trace principle

实现信号解调,不仅需要载波频率跟踪,还需要完成载波相位的恢复,为此采用锁频锁相环,用FLL辅助PLL 可以消除大的频偏对PLL 的影响,将载波频率快速牵引至PLL 的锁定范围,保证PLL 稳定入锁。 锁频环采用一级FRFT 加一级FFT 经二阶滤波器的方式实现。 FRFT 较FFT 的不同在于FRFT 在搜索阶数的间隔α 均匀时,对应的Δμ 是不均匀的,而是对应cotα。 也就是说,搜索阶数在多普勒频率变化率低时更密集,在多普勒频率变化率高时更稀疏。 利用这个特点,先用FFT 进行峰值搜索,确定信号多普勒频率变化率范围的粗略估计区间,再用FRFT 进行峰值搜索,确定峰值的精确位置,精确估计多普勒频率变化率。 FLL 的积分时间长短会影响鉴频器的频率牵引范围,积分时间越长,入锁范围就越小,当频率偏移超过入锁范围时,FLL 可能失锁[11],但积分长度越长,环路带宽越窄,性能越好。因此FFT 点数的选择根据符号速率和多普勒频率变化率的相对关系选取,当多普勒频率变化率大于符号速率时,FFT 点数不大于64(FFT 计算点数可适当加长)。 在FLL 辅助PLL 的锁频锁相环中,FLL仅用作PLL 的牵引,主要用途是扩大跟踪范围[13-14],为此FFT 模块采用滑动输入的方式,每个符号计算一次频率估计值。 采用2 次锁频环辅助锁相环可以将跟踪范围扩大为导频符号速率的2 倍。FLL 辅助PLL 的锁频锁相环框图如图5 所示。

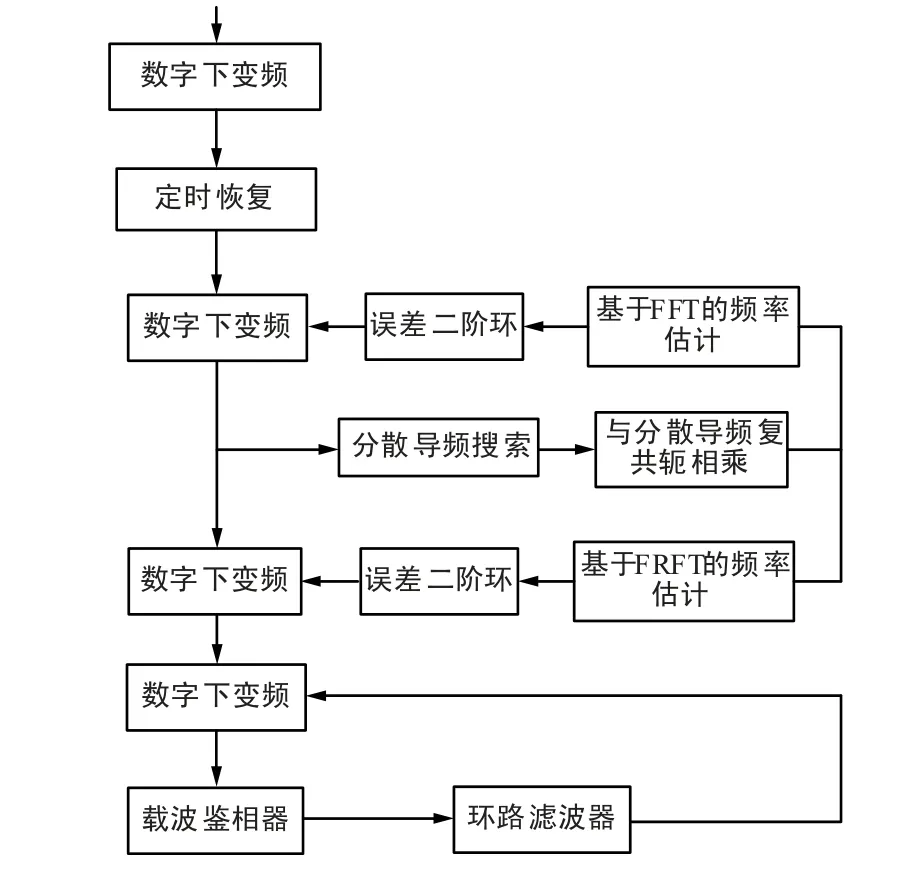
图5 基于分散导频的载波跟踪原理框图Fig.5 Carrier frequency trace principle based on disperse pilot code

3 仿真分析

在信息速率为Rs 时,如果采用调制方式为QPSK,LDPC 码的码率为1/3 时,符号速率为1.5Rs,分散导频一般为符号速率的1/10 左右(依据具体帧结构确定),也就是0.15 倍Rs,多普勒频率变化率可达分散导频速率的1.5 倍,也就是符号速率的0.225 倍。 大的多普勒频移在解调时,采用FRFT 结合FFT 的方法完全可以完成信号的捕获。多普勒频率变化率作为载波恢复误差的方差会对解调性能造成一定影响。 下面仿真载波恢复误差的方差对解调性能的影响[15],仿真结果如图6 所示。

对于1.5 倍Rs 的符号速率,0.225 倍Fs 的多普勒频率变化率约为符号速率的1.5×10-1。 从图6 的仿真结果可知,对于信息速率为Rs 的信号,多普勒频率变化率造成的载波误差对解调性能的影响性能损失可达1.5 dB 以上,甚至导致载波锁相环不能入锁。

因此,为了减小多普勒频率变化率对解调性能的影响,需要对解调器接收的信号进行多普勒频率及其变化率的精确跟踪[16-17],可以通过锁频锁相环实现,即用一级FRFT 加一级FFT 的算法实现大的多普勒频率变化率的跟踪,引导锁相环快速入锁,完成载波相位恢复。 原理框图如图7 所示,对于采用分散导频的信号,在Es/N0=-1 dB 下的QPSK 信号,多普勒变化率为2 倍Rs/s 时的频率跟踪仿真图如图8 和图9 所示,仿真结果表明,采用本算法可以完成多普勒频率的跟踪。

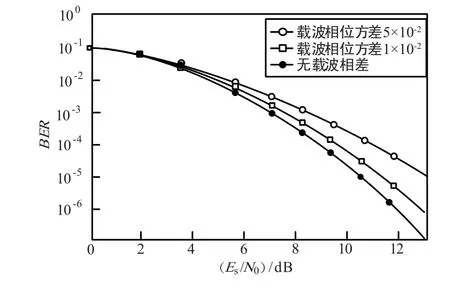
图6 误码率特性仿真曲线Fig.6 Code error performance emulation curve

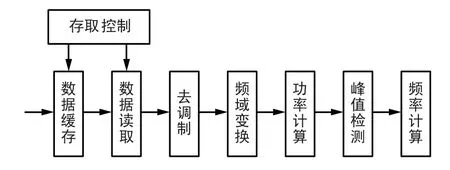
图7 多普勒频率计算原理图Fig.7 Dopler frequency calculate principle

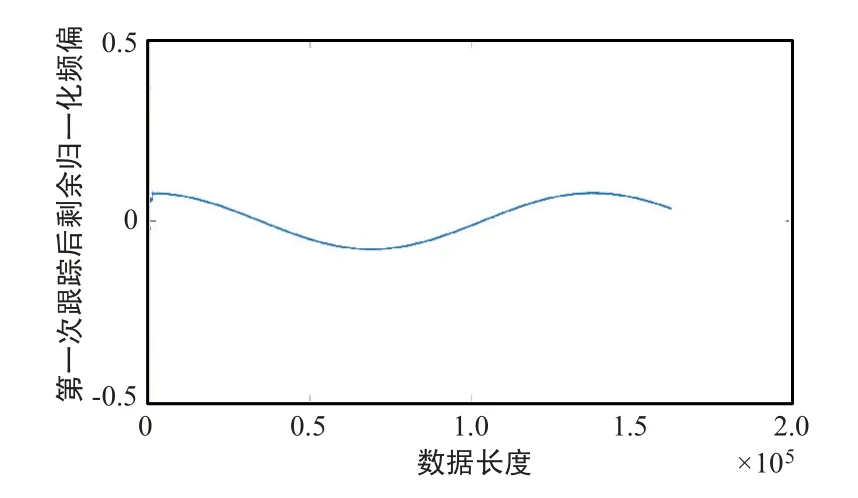
图8 正弦模型1 次2 阶锁频环频率跟踪仿真图Fig.8 1-time 2-order frequency and phase loop frequency trace emulation based on sine model

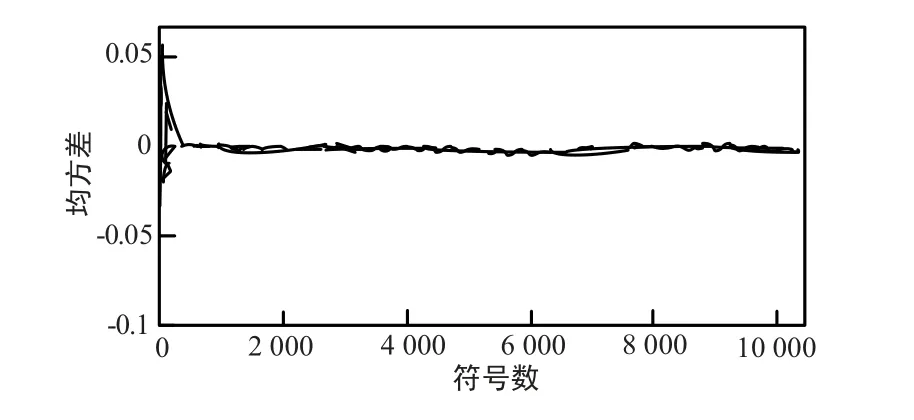
图9 正弦模型2 次2 阶锁频环频率跟踪仿真图Fig.9 2-time 2-order frequency and phase loop frequency trace emulation based on sine model

采用正弦模型,对于多普勒变化率为2 倍Rs/s的QPSK 信号,在接收端完成多普勒频率跟踪,通过调制端反向补偿后,对接收端信号进行频率估计仿真。 仿真结果表明,通过调制端多普勒补偿,有效对抗了上行链路的多普勒频率频移,在接收端剩余的多普勒频移不超过符号速率的1%,对信号的捕获和解调性能没有影响。

采用JPL 模型,对Es/N0= -1 dB 条件下的QPSK 信号,多普勒变化率为2Rs/s 时的频率跟踪仿真如图10 和图11 所示。 仿真结果表明,采用此算法可以完成多普勒频率的跟踪。

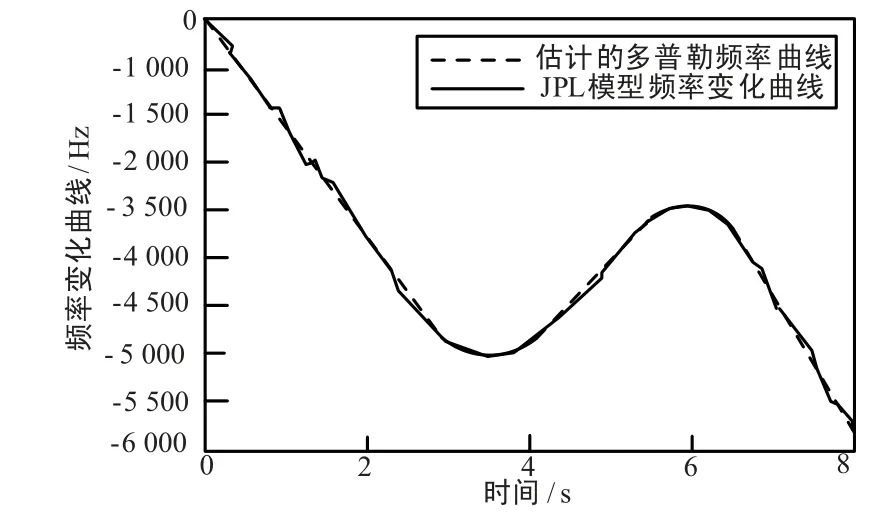
图10 JPL 高动态下的多普勒频率跟踪曲线Fig.10 Dopler frequency trace curve based on JPL high dynamic model

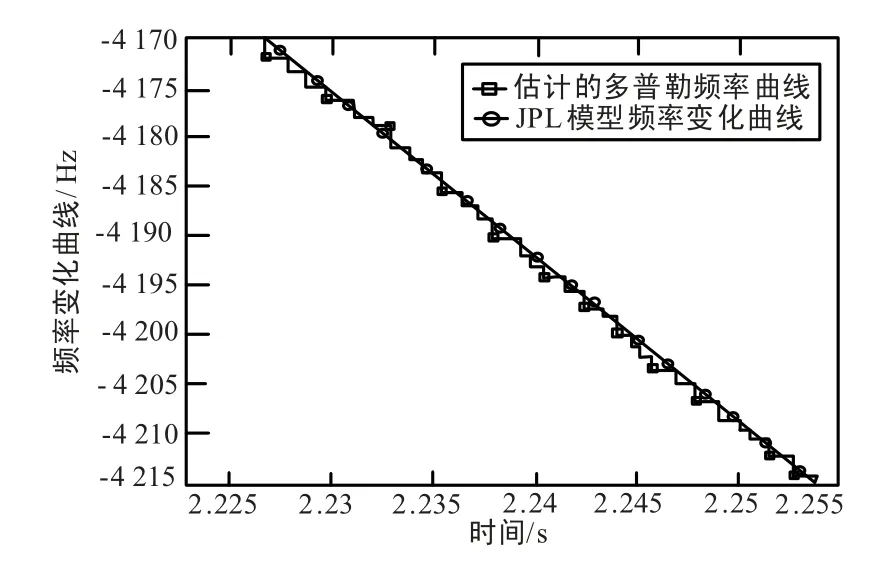
图11 JPL 高动态下频率跟踪曲线局部放大图Fig.11 Local part zoom out of frequency trace curve based on JPL high dynamic model

根据仿真的误码统计结果,对于符号速率10 ksps的信号,导频速率为1 ksps。 算法可以在±6 kHz 的频偏范围内跟踪1.5 kHz/s 的频率变化。 接收的解调误比特率为0.023,相比QPSK 调制的理论解调BER 曲线,性能损失为0.11 dB,满足系统设计要求。

对FRFT+FFT 算法和传统FFT 算法进行比较,如图12 所示。 从仿真结果可以看出,FRFT+FFT 算法从跟踪范围、收敛速度及跟踪精度等方面都优于传统的FFT 算法,FRFT+FFT 算法跟踪范围可达导频符号速率的2 倍,可在500 个导频符号内快速收敛,跟踪误差小于5‰。

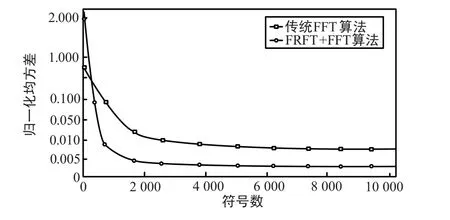
图12 正弦模型2 次2 阶锁频环频率跟踪精度比较Fig.12 Comparative fig of 2-time 2-order frequency and phase loop frequency trace precision

4 结束语

针对低信噪比、高动态环境下多普勒频移及频率变化率大和信号跟踪相对困难的特点,采用了分散导频的信号结构,研究了分数阶傅里叶变换针对跟踪高动态信号的应用[18],利用简化的FRFT 结合FFT 算法设计了高动态接收机信号跟踪环模块[19-20],计算得出高动态信号的多普勒频率和多普勒频率变化率,以达到跟踪到高动态信号的目的;该方法在保证精度的同时,减小了运算量,仿真结果证实了该算法的可行性和正确性。 在硬件实现测试,可以满足高动态信号跟踪的精确性、实时性。