基于TDOA 的网络化定位系统自适应站点优选算法

杜 盈,陈 峻

(中国电子科技集团公司第七研究所,广东 广州 510310)

0 引言

航天发射场是科学卫星、技术试验卫星及运载火箭的发射试验基地,荟萃了多项先进的航空航天科学技术的最新成果。 近年来,无人机市场蓬勃发展,航天发射场成为无人机“黑飞”的频发场所,许多私人无人机飞入基地,利用无人机偷窥重要航天技术,探寻国家机密、获取国家情报、危害国家安全,甚至造成不堪设想的后果。 无源时差定位(Time Difference of Arrival,TDOA)技术[1-2]由于其定位原理简单、定位精度高、抗多径干扰能力强等特点,被广泛应用于无人机目标信号的定位[3]。 利用测量信号到达不同传感器站点的时间差方法,根据双曲线交叉原理求出目标位置,单一目标的定位只需要基于少量(如4 ～8 个)站点数据完成[4-5]。 但实际应用中无人机信号辐射强度弱,具有较高灵敏度的传感器也只能接收到有限范围内的频谱信号,无法满足大型发射场等重点区域的覆盖要求。

与传统定位系统相比,网络化无源多点定位系统是由部署在观测区域内若干无源传感器站点采用无线方式组建的自组织网络,具有大规模灵活部署和扩展,以及网络高度动态等特点。 该系统作为一种新的航天发射场监视技术,通常情况下,可以通过传感器站点周期性地或触发式地将感知信息传送至融合中心,然后利用TDOA 技术对重要区域内的低空目标进行定位。 但是,当网络站点数量较多时,对所有站点进行信号采集传输将造成大量能量及网络资源的浪费。 此外,选用不同站点数量和不同位置的站点会对定位精度产生影响。 因此,密集网络化无源定位系统中高效、高定位精度的站点优选策略已经成为该应用领域一个关键的研究方向。

针对传统的三点或四点无源定位方法,目前已有的文献主要通过概率统计、误差分析的方法研究站点几何分布等因素对定位精度的影响情况[6-7]。文献[6]研究表明辐射源位于三角形内部且3 个站点位置呈锐角三角形排列时,可大幅度提高定位精度。 文献[7]讨论了4 个站点以三角型、星型等不同布站方式,分析基线长度变化、目标位置变化对定位精度的影响,并给出最优布站示意图。 文献[8]提出一种改进的混沌双扰动粒子群算法对基站和待测目标连线水平角的非线性函数寻优,并总结归纳了最优布局时3 个定位基站拓扑结构的特点。 文献[9]提出以Cramer-Rao 界平均值最小化为目标,采用遗传算法全局搜索最优布站站点组合,该算法需要事先确定有效定位区域并以此限定Cramer-Rao 界计算范围,只适用于定位区域较小的场景。文献[10]以实际监测频谱数据信号信噪比(Signalto-Noise Ratio,SNR)为基础,结合锐角三角形布站准则,提出一种用于多站TDOA 定位技术的自动选站算法,但该算法只针对三站定位系统,而无法对4 个以上的站点进行优选。 文献[11]根据浦东机场的布局特点,采用倒三角型与星型布站构型相结合的站点部署方案,为网络化无源定位系统的物理选址提供了一定参考。

本文讨论结合当前各站点无人机信号识别结果,利用K 均值聚类算法动态调整当前目标定位空间,进而对网络化TDOA 无源定位系统的站点优选问题加以研究。 站点优选的目标是形成在所得到的当前目标定位空间内,在已识别出无人机信号的站点集所构成的所有不同定位站点组合中,寻找针对当前目标定位空间形成最优布站的站点组合,即满足Cramer-Rao 界均值最小原则。 该算法能够解决航天发射场大规模密集网络化无源定位系统中针对目标空域范围定位的高效、高精度的站点选择问题。

1 问题描述及Cramer-Rao 界分析

考虑在网络化TDOA 无源定位系统中包含M ≫4 个站点pi(xi,yi,zi)(i=1,2,…,M) ,分布在Ω：{z = 0,x2+ y2≤R2} 的圆形区域内,目标定位的责任区域为Φ：{0 ≤z ≤H,x2+ y2≤R2} 的圆柱形立体空间。 当目标定位责任区域Φ 内出现低空目标p0(x0,y0,z0) ∈Φ 时,通过在M 个站点中选出N 个(如N = 4)站点组合,使得以N 个站点pi(xi,yi,zi)(i =1,…,N) 为参考,对以p0(x0,y0,z0) 为中心,R’ 为半径的空间Г 中目标进行定位的定位误差平均Cramer-Rao 界最小[12]。

在高斯噪声环境下,TDOA 定位系统在空间某点(x,y,z) 的定位误差的Cramer-Rao 界为[13]：

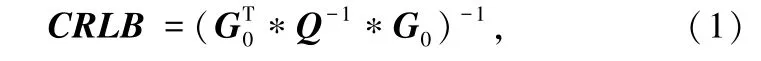
式中,CRLB 矩阵对于参与定位的站点pi(xi,yi,zi)具有对称性,即以任意一个参与定位的站点作为TDOA 定位算法的中心参考点,计算得到定位误差的Cramer-Rao 界不变。 因此,不失一般性地,假设以 p1(x1, y1, z1) 为基准参考站点,则G0∈为：

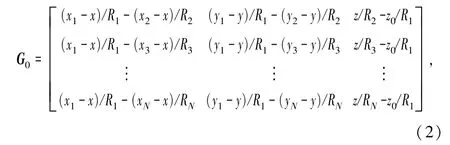
式中, Ri为站点 pi(xi, yi, zi) 到空间定位目标(x,y,z) 的距离,即

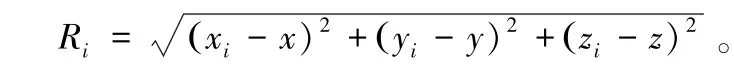
测量值误差协方差矩阵Q 定义为：

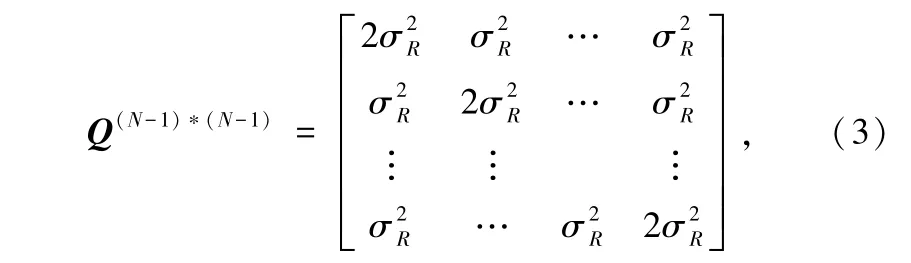
式中,网络中各站点测得的到达时间测量值之间相互独立,且服从标准差为σi的高斯分布,采用与到达时间测量误差相对应的距离误差的标准差σR=c∗σi代替σi,可得TDOA 测量值误差协方差矩阵Q。 由式(1)可得,基于TDOA 的定位系统在以目标(x,y,z) 为中心的立体空间Г 内的定位精度的Cramer-Rao 界平均值的表达式为：

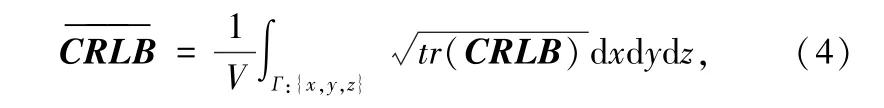
式中,V 为立体空间Г 的体积。

2 基于Cramer-Rao 界的自适应站点优选算法

自适应站点优选的目标是针对定位责任空间中任意一个目标点p0(x0,y0,z0) ,从网络中选出N 个站点的定位组合,使该组合对以p0(x0,y0,z0) 为中心,R’ 为半径的立体空间Γ 中所有点分别进行定位的Cramer-Rao 界的均值最小。

由于立体空间Γ 的中心即为目标 p0(x0,y0,z0),事先无法获取,因此可以考虑采用K 均值聚类算法求取的已识别无人机信号站点集的聚类中心位置() 来近似作为立体空间Γ 的中心点。K 均值聚类算法是目前应用广泛且成熟的一种划分式聚类分析算法[14-15],能使聚类域中的所有数据对象到聚类中心距离平方和最小。 算法基本思路为：随机选择k 个数据对象作为初始聚类中心,计算n 个数据对象到k 个聚类中心的距离d,找出最小距离,把所有数据归入与它距离最近的聚类中心,修改中心点的值为本类所有数据对象的均值。 若相邻迭代次数内聚类中心值的变化超过规定的阈值,则根据新的聚类中心对所有数据对象进行重新划分;若相邻迭代次数内聚类中心值的变化小于规定的阈值,则算法收敛,输出聚类结果,设迭代次数为t 次。

在已识别无人机信号的站点集构成的所有不同定位站点组合中,寻找针对以() 为中心,R′为半径的近似目标定位空间中Cramer-Rao 界均值最小的最优站点组合,即为最终优选结果。

下面给出自适应选站算法的具体流程：

步骤 1：各站点设置频率监测计划,中心站周期地(如每0.1 s)从网络中接收获取网络中所有站点的频谱监测数据。

步骤2：对频谱数据进行宽带频谱特征分析,首先通过信号能量检测,识别信号带宽和中心频率,再与频谱库对比分析,判断是干扰信号还是无人机信号,最后筛选出已识别无人机信号的站点,并对站点进行编号i = 1,2,…,保存站点坐标至S(i) 。

步骤 3：确定Cramer-Rao 界的范围：

① 对S(i) 中元素采用K 均值聚类算法,聚类结果作为Cramer-Rao 界的中心点() ;

步骤4：从S(i) 中遍历任意N 个站点的组合,根据式(3)计算其Cramer-Rao 界平均值,并存入数组C(j) 中,数组中最小值所对应的N 个站点即为最佳选站结果。

从上述流程分析可知,K 均值聚类算法时间复杂度为O(k ×n ×d ×t) ,空间复杂度为O(n ×d) 。一般k, d, t 均可认为是常量,所以时间和空间复杂度简化为O(n) ,即线性的。 Cramer-Rao 界均值算法从M 个站点中选出N 个( N 一般取值为4 ～8)站点组成TDOA 定位系统,其定位误差的CRLB 矩阵相乘、求逆的复杂度均为O(n^3) ,而Cramer-Rao界平均值是CRLB 矩阵的三重积分,因此算法复杂度即为O(n^3) 。

在实际应用中,由于无人机高速飞行过程中到各站点信道的时变衰落特性,导致每秒筛选出的传感器站点数组可能都不一样。 采用本文提出的基于信号识别和Cramer-Rao 界范围的节点动态更新机制,确保中心站能够从网络中选择出N 个站点进行定位,有效跟踪无人机的轨迹,在没有大幅度提升计算复杂度的情况下,实现了多点定位网络的自适应站点优选。

基于Cramer-Rao 界自适应站点优选算法流程如图1 所示。

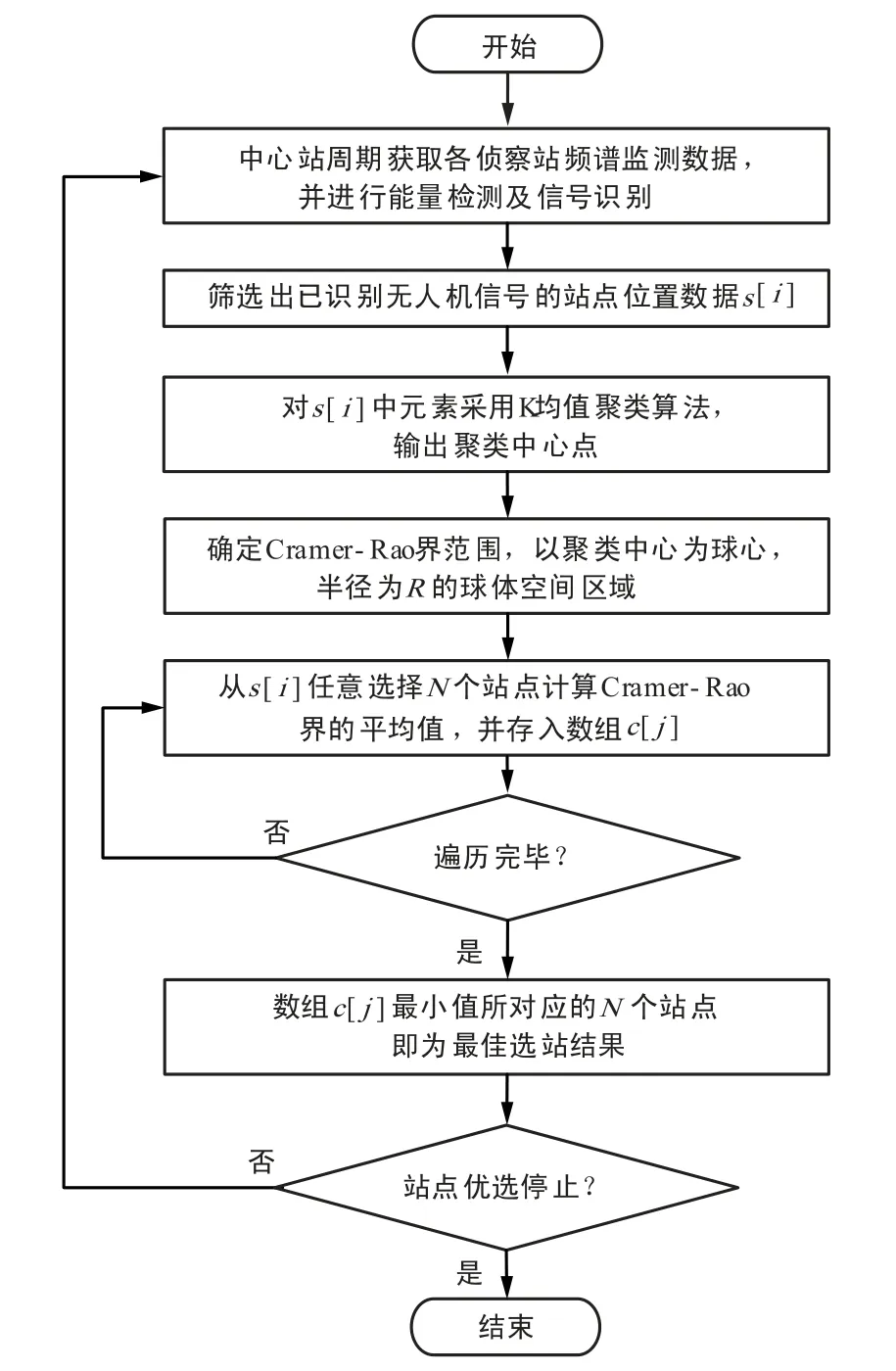
图1 自适应站点优选算法流程图Fig.1 Flow chart of adaptive optimize embattle method

3 仿真实验与分析

实验1 假设布站范围及定位责任范围限制在半径为1 km 的圆形区域内,区域中心位于原点。 并假设每次仿真实验中,在布站范围内随机均匀布设M = 4 个传感器站点,每次定位所用的定位目标随机在定位责任范围内生成,高度服从[0,200]上的均匀分布。 每次参与TDOA 定位的站点个数为N = 5,即采用不同的选站算法在200 个站点中选出5 个站点进行定位。 实验主要仿真对比2 种选站算法：① 随机选择法,即随机选择5 个已识别无人机信号的站点;② 本文所提优选算法,为便于对比分析,实验均采用经典的Chan 算法定位[16],并假设与定位目标直线距离小于300 m 的站点可识别出无人机信号。 仿真中不同算法对应的定位精度均通过2 000 次独立试验进行平均得到。

图2 为对采用不同算法得到的选站结果进行TDOA 定位的定位误差随站点到达时间(Time of Arrival,TOA)噪声方差[17-18]变化的仿真结果。 由图2 可知,随着TOA 噪声方差的增大,2 种选站算法得到的选站结果所对应的TDOA 定位精度逐渐降低。 并且本文提出的选站算法所得到的TDOA 定位精度在不同TOA 噪声方差条件下,均优于与之比较的另一种算法。 例如,当TOA 噪声方差为2. 5 ns时,所提算法的定位精度能够达到18 m,而另一算法的定位S 精度只能达到22 m 左右。

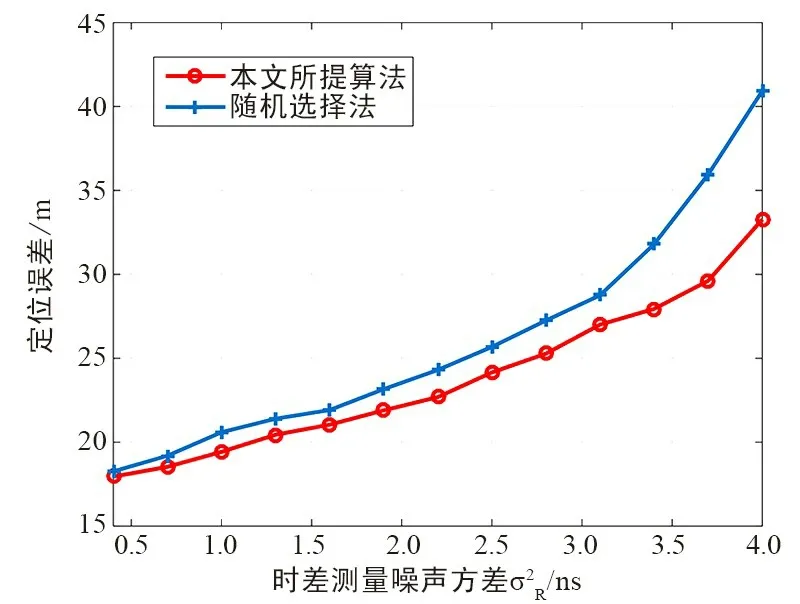
图2 不同选站算法TDOA 定位误差 vs.TOA 噪声方差Fig.2 TDOA positioning error vs.TOA noise variance in different station selection algorithms

实验2 同样考虑半径1 km 圆形区域的布站范围及定位责任范围,随机均匀布设200 个传感器站点,每次定位目标随机生成,高度服从[0,200]均匀分布,TOA 噪声方差为2 ns。 每次参与TDOA 定位的站点个数N 为5,…,11。 仿真对比实验1 中所用的2 种选站算法。

图3 为采用不同算法得到的选站结果进行TDOA 定位的定位误差随定位站点个数变化的仿真结果。 由图3 可知,当TDOA 定位站点数量小于等于9 时,2 种选站算法得到的选站结果所对应的TDOA 定位精度随定位站点数量的增加而提高。 但当定位站点个数大于9 时,本文所提算法对应的定位精度不再随站点增加而变化,可见在该仿真参数设定条件下,所提算法只需要9 个站点,即可在该场景下获得稳定的高精度定位性能,而另一种算法则至少需要约11 个站点才能达到稳定的定位精度。

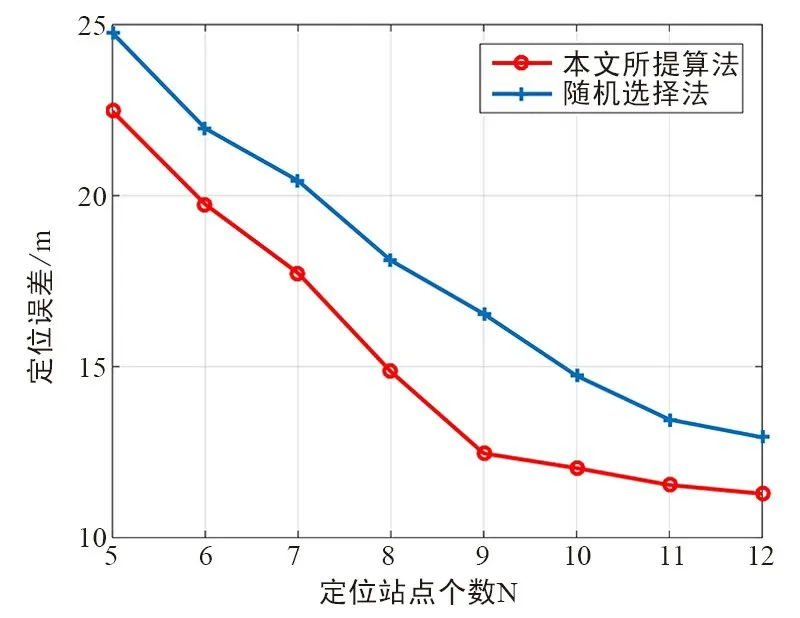
图3 不同算法TDOA 定位误差 vs.定位站点个数Fig.3 TDOA positioning error vs.number of sites in different algorithms

4 结束语

由于网络化TDOA 无源定位系统引入了大量密集分布的频谱感知站点,既要尽可能有效地利用多个站点的数据信息提高定位精度,又要平衡系统通信开销及计算压力。 本文提出的自适应站点优选算法根据空中目标移动特性,不断更新实际可用站点及Cramer-Rao 界范围,利用Cramer-Rao 界为目标函数获取最小均值所对应的最优站点组合参与TDOA 定位,解决网络化TDOA 定位系统中最佳站点选择策略的问题,该方法适用于大规模密集网络化无源定位系统中针对空间任意目标的定位站点优选,算法快速收敛,具有工程实用价值。