一种基于LMMSE 改进的FBMC 信道估计算法

王献炜,颜 彪,王应元,周 琦,王梦实

(扬州大学 信息工程学院,江苏 扬州 225009)

0 引言

正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)是一种多载波调制(Multi Carrier Modulation,MCM)[1-3],其对于多径信道具有良好的性能。 但是OFDM 存在一些缺点,比如高的带外泄漏和因为循环前缀而导致的低频谱利用率[4]。为了弥补这些缺点,滤波器组多载波技术(Filter Bank Multicarrier,FBMC)被提出[5],同时还引入了交错正交幅度调制(Offset Quadrature Amplitude Modulation,OQAM)来减少系统本身的干扰[6]。 FBMC/OQAM 技术被认为是第五代移动通信中非常具有潜力的一个备选技术[7-9]。

然而,由于使用原型滤波器的原因,FBMC/OQAM 系统仅满足实数域正交,这导致当信号通过发送滤波器进入复数信道的时候会产生虚部干扰,信道估计变得更加复杂。 与OFDM 中的信道估计相比,FBMC/OQAM 中的主要问题在于对虚部干扰的处理。 文献[10-11]提出基于导频的干扰逼近(Interference Approximation Method,IAM)算法和干扰消除(Interference Cancellation Method,ICM)算法,但是采用的都是最小二乘(Least Square,LS)算法,没有考虑噪声在信道估计中的影响。 文献[12]提出基于最小均方误差(Minimum Mean-Square Error,MMSE)的信道估计算法,把噪声的影响考虑进去,但是实施的复杂度过高。 文献[13]提出基于MMSE算法改进的线性最小均方误差(Liner Minimum Mean-Square Error,LMMSE)算法,但是改进后的LMMSE 算法仍然具有较大的运算复杂度。

本文对传统的LMMSE 算法进行了改进,将在OFDM 信道估计中常用的DFT 算法结合LMMSE 算法,并采用迭代的方法分别获得信道先验信息和最佳的信道估计,同时采用矩阵的SVD 分解算法有效降低运算复杂度。 最后的仿真表明改进后的算法明显提高了系统的性能。

1 FBMC/OQAM 系统

FBMC/OQAM 的系统基带传输模型框图如图1所示。 系统等效基带发送信号表示为：

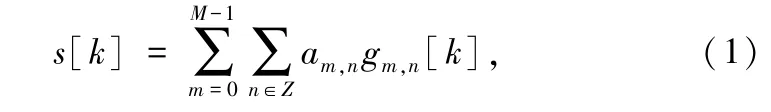
式中,am,n表示经过OQAM 调制后的符号,m 和n分别表示在子载波和时间位置上的索引, gm,n[k]表示发送端等效滤波器：

式中,g[k] 表示原型滤波器,此处的原型滤波器采用Hermite 原型滤波器[14]。

图1 FBMC/OQAM 系统基带传输模型Fig.1 FBMC / OQAM system baseband transmission model

通过信道后,接收信号可以表示为：

式中,Hm,n表示信号在时频格点(m,n)位置的信道响应。 接收端的等效滤波器做内积后得到解调信号

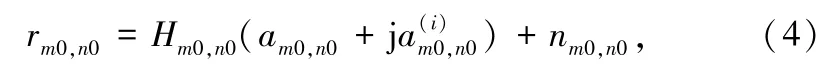
式中nm0,n0= ＜nm0,n0| gm0,n0＞表示经过解调后的噪声,表示滤波器组内部产生的虚部干扰。

2 LMMSE 信道估计算法分析

FBMC/OQAM 系统中的信道估计是基于导频获得,导频信号被插入发送数据信号中,接收机利用接收到的导频信号和本地产生的信号进行信道估计。

LS 信道估计算法的目的是使接收信号和理想信号之间的距离平方和最小[15]。 即

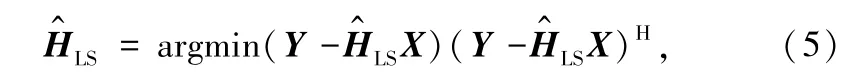
式中,Y 表示接收信号,X 表示发送信号。 经化简,算法可以表示如下：

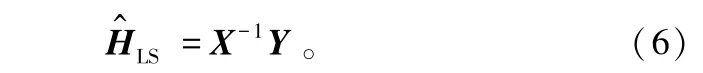
由式(6)可以看出,LS 算法忽略了噪声的影响,为了进一步解决噪声的问题,提出了LMMSE 算法。LMMSE 算法是一种优化的MMSE 算法[16]。 MMSE算法的目的是使接收到信道估计和理想的信道估计的均方误差最小,即

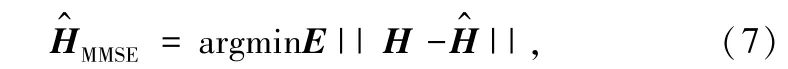
经简化可以表示为：

式中,RHH表示信道的自相关矩阵,表示噪声的功率。 当资源块数量非常大时,计算(XXH)-1复杂度非常高。 因此提出了改进后的LMMSE 算法,利用E{(XXH)-1} 代替(XXH)-1,改进后算法表示如下：

式中,β 根据不同的调制方式决定,采用QPSK 时,设置β = 1,采用16QAM 时,设置β = 9/16。

3 改进后LMMSE 信道估计算法

为了提高LMMSE 算法的性能并降低运算复杂度,本文提出一种改进的LMMSE 算法。 首先对采用基于DFT 的信道估计算法对导频得到的信道估计进行计算[17],步骤如下：

① 根据式(9),使用LS 算法获得H^LS。

② 使用IDFT 将H^LS转换到时域：

式中,w^(m) 表示时域中的噪声部分。

③ 对h^LS进行截短,减少噪声的影响：

④ 把h^DFT通过DFT 变换到频域：

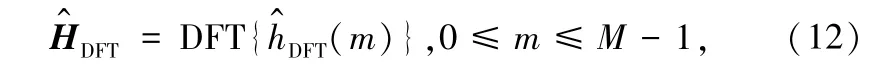
其中,Le的长度可以选取1/4 子载波的长度。 第一步改进后,式(9)可以表示如下：

由式(13)可以看出,信道估计的获得依赖于信道的协方差矩阵,在这种情况下是先验未知的。 文献[18]提出一种通过迭代获得信道相关矩阵的方法,把这种方法应用于本文系统中,步骤如下：

② 获得初始的信道相关矩阵：

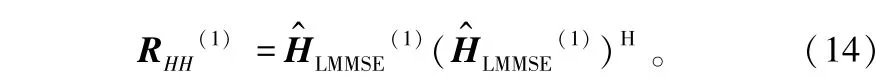
④ 估计噪声方差：

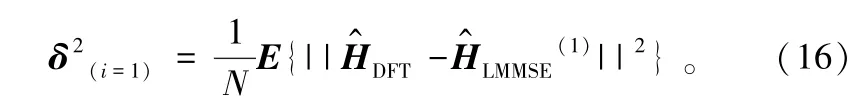
⑤ 计算更精确的信道相关矩阵：

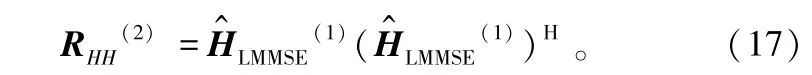
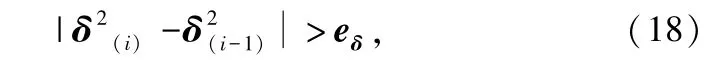
其中,eδ是一个选择的最佳门限值。

把获得的最优信道相关矩阵表示为RHHopt 代入式(13),得到最终的改进LMMSE 算法表达式：

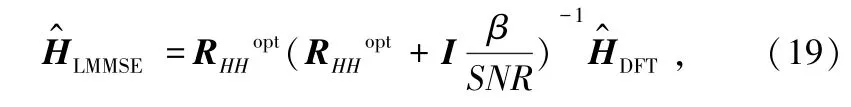
最终改进的LMMSE 算法性能有了明显的改善,但同时因为迭代的计算也提升了运算的复杂度。 采用一种矩阵的SVD 分解算法来计算RHH：

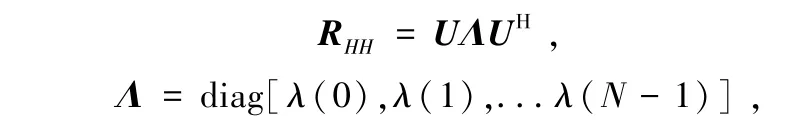
所以,式(19)可以转换为：

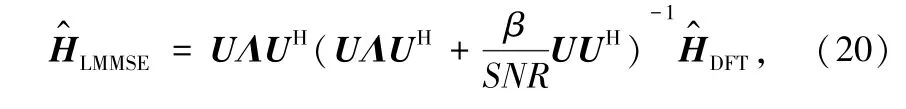
避免了矩阵求逆的计算。

4 仿真分析

对提出的改进LMMSE 信道估计算法进行Matlab 仿真,系统的仿真参数值如表1 所示。

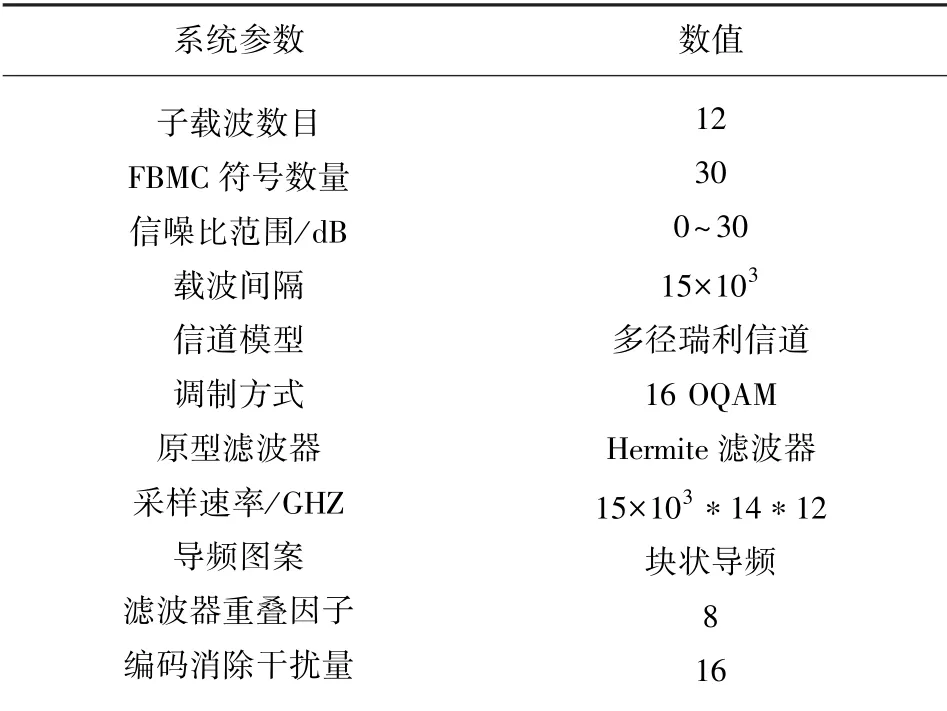
表1 仿真参数设置Tab.1 Simulation parameter setling

由于FBMC/OQAM 系统本身并不满足实数域正交,导致周围数据符号对导频干扰。 采用文献[12]提出的预编码干扰消除算法来消除导频周围数据符号的干扰,预编码导频图如图2所示。

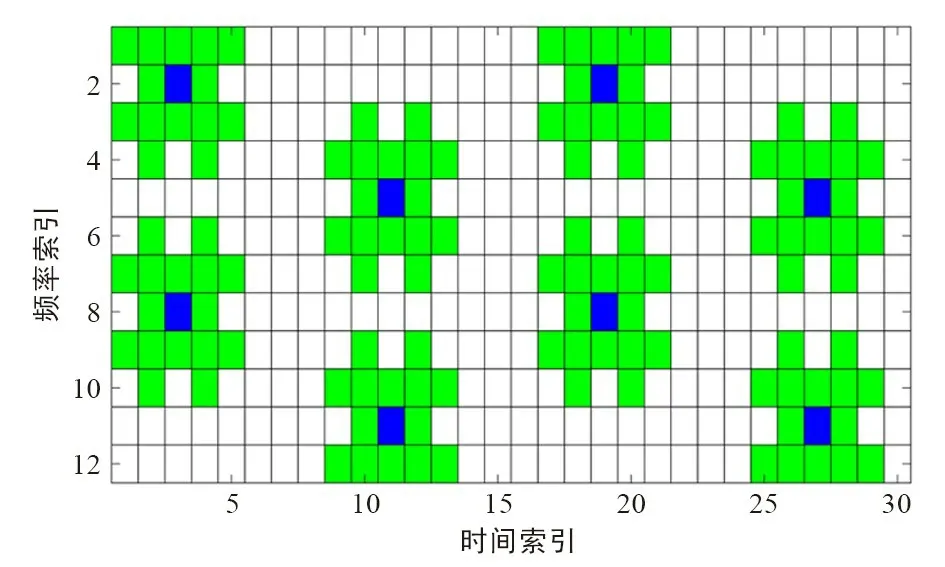
图2 预编码导频图Fig.2 Precoding pilot pattern

利用新提出的FBMC 信道估计算法得到的误比特率(Bit Error Rate,BER)与信噪比 (Signal Noise Ratio,SNR)仿真曲线图如图3 所示,图中还列出了其他几种传统信道估计算法的BER 和SNR 仿真曲线图。

图3 BER 与SNR 曲线图Fig.3 BER and SNR curve

从图3 的比较可以看出,新提出的信道估计算法比传统的LS 信道估计算法和传统LMMSE 的信道估计算法能都要好。

5 结束语

本文借鉴了OFDM 系统中的LMMSE 信道估计算法,对其进行了改进,通过预编码的方法将其成功运用于FBMC/OQAM 系统中,同时引用了DFT 的方法进一步减少干扰。

实验结果表明,通过对信道的建模验证了算法的正确性。 该算法在一定程度上解决了FBMC/OQAM 系统在信道估计方面实现的难点,也为将来加入MIMO 的研究打下了基础。