基于细节比的汽车曲线品质评定方法研究＊

闫晨 纪小刚,2 于益超 胡海涛 张溪溪

（1.江南大学，无锡 214122；2.江苏省食品先进制造装备技术重点实验室，无锡 214122）

主题词：车身曲线品质 定量评定 细节比 标定

1 前言

车身重构曲线曲面的品质影响着汽车及其零部件的性能、加工制造以及外观设计。目前，车身曲线曲面的品质评定方法主要有曲率分析法、光照模型法和辅助面法[1-4]，然而上述方法无法进行定量评价，且主要由人工进行评定，往往带有很强的主观性，受到分析人员经验、视觉误差、终端分辨率等多种因素的制约，缺乏客观、统一的评定依据，导致车身曲线曲面的品质评定结果主观性强、准确度差且评定效率低下。因此，需要一种客观、统一的定量评定方法对车身曲线曲面品质进行评定。

评定人员的经验和观点以及用户的要求和意愿都具有很强的模糊性，需要把主观与客观评定相结合，将这种模糊性进行解析和量化，模糊数学理论中的模糊综合评判方法为解决这类问题提供了有效途径，通过建立起面向对象的综合评定体系[5-8]，得到评定车身曲面品质的定量值，从而得到相对客观、准确的结论，但这类方法操作过于复杂且需要耗费大量人力，因而效率低下，实用性不强。

近年来，小波分析技术在曲线造型领域应用越来越广泛[9-11]，通过小波分解过滤掉曲线的缺陷，并保持原曲线的整体趋势，可达到优化曲线品质的目的。曲线小波分解后可得到尺度部分（反映曲线的本质特性，即光顺信息）和细节部分（反映曲线的外在缺陷，即细节信息），这两部分均可量化，对尺度部分和细节部分进行综合利用，构建用于评定车身曲线品质的指标，可实现定量化评定。针对现阶段曲线曲面品质评定方法的缺陷，本文通过曲线的小波分解，提取曲线品质优化后得到的信息，定义曲线的细节比，由细节比的性质对不同品质的曲线进行标定，得到曲线品质等级表，实现对曲线品质的定量评定。

2 细节比的定义及其性质

由于目前主流的三维造型软件多使用准均匀B样条进行曲线曲面造型，同时，高次B样条曲线的局部性较差，且幂次越高计算量越大，在实际工程应用中多使用不超过三次的B样条，因此，本文以准均匀三次B样条曲线为例进行说明。

尺度j下基函数为Φj、控制顶点矩阵为Cj的准均匀三次B样条曲线fj(t)=ΦjCj经小波分解后可以得到尺度曲线fj-1(t)和细节曲线gj-1(t)，即

式（1）用矩阵形式可表示为：

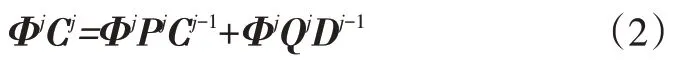
式中，Pj为尺度曲线重构矩阵；Cj-1为尺度曲线控制顶点矩阵；Qj为细节曲线重构矩阵；Dj-1为细节曲线控制顶点矩阵。

对曲线执行多次小波分解可得：

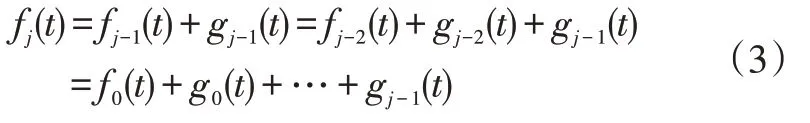
式中，fi(t)(i=0,1,…,j-1)为曲线每次分解后得到的尺度曲线；gi(t)(i=0,1,…,j-1)为曲线分解后得到的细节曲线，用矩阵形式可表示为ΦjCj=ΦjPjCj-1+ΦjQjDj-1=ΦjPjPj-1Cj-2+ΦjPjQj-1Dj-2+ΦjQjDj-1=ΦjPjPj-1…P1C0+ΦjPjPj-1…P2Q1D0+…+ΦjPjQj-1Dj-2+ΦjQjDj-1。

由矩阵的运算规则可知：

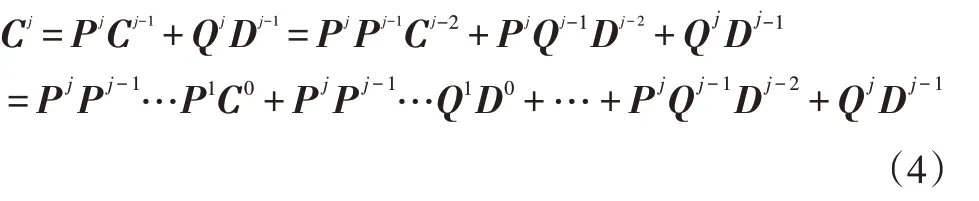
式中，PjPj-1…P1C0为多次光顺后得到的尺度曲线控制顶点，代表曲线所含的光顺信息；PjPj-1…Q1D0、……、PjQj-1Dj-2、QjDj-1为曲线多次光顺得到的所有细节曲线控制点，代表曲线所含的全部细节信息。

定义曲线细节比为：

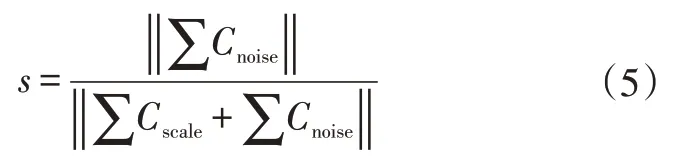
式中，||·||为矩阵范数，本文采用F范数；∑Cnoise为曲线所含的细节信息总和；∑Cscale为多次光顺后得到的曲线光顺信息总和。

结合式（4）可得：

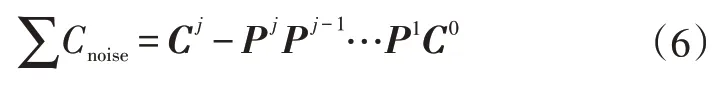
则细节比的定义式（5）可变为：

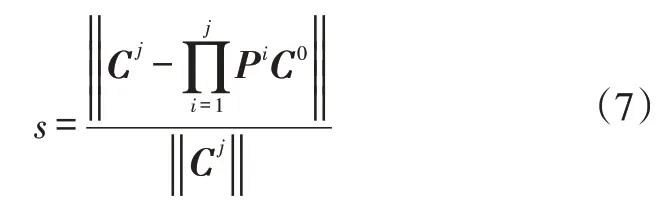
由细节比的定义可知：0≤s≤1；s越大，则曲线包含的细节信息越多，曲线的品质越差；反之，则细节信息越少，曲线的品质越好。

在计算细节比时，需要说明的是，由于B样条曲线具有几何不变性，处在不同坐标下的同一曲线有相同的细节，但细节比数值大小不同，为减小坐标对细节比数值的影响，在计算细节比前需对曲线进行平移变换，将控制点变换到以原点为中心，对于三维控制点为CM×3（M为曲线控制点数）的任意曲线，先将控制点矩阵加上一列全为1的列向量，扩充为M×4的矩阵CM×4，变换矩阵为：

其中，(cx,cy,cz)为原曲线控制点中心坐标，变换后的矩阵为：

变换后的控制点矩阵为CCM×4的前3列，由新的控制点进行光顺处理计算曲线的细节比。

3 曲线的细节失真及其修正

3.1 曲线的细节失真

为得到曲线全部的细节信息，需要对曲线做多次小波分解，对于准均匀三次B样条曲线，其控制点至少应为4个，所以可将曲线光顺到4个控制点以得到全部的细节信息，根据准均匀三次B样条的定义，当曲线尺度m=10时，共有u=m+3=13个基函数，节点矢量T=[0,0,0,0,1/m,…,1-1/m,1,1,1,1]=[tv](v=1,2,…,u+4)定义的准均匀三次B样条基函数Φ=[Bu(tv)]如图1所示。

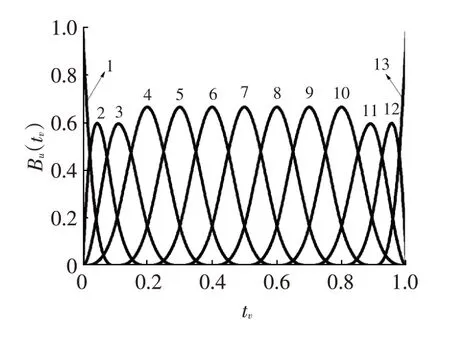
图1 m=10对应的准均匀三次B样条基函数

其中第1～3个和第11～13个基函数图像为非均匀B样条基函数，第4～10个基函数可看作由第4个基函数平移得到，是均匀B样条基函数。对于准均匀三次B样条而言，其首尾6个基函数均为非均匀基函数，剩余的基函数均为均匀基函数，当曲线控制顶点较少时，非均匀B样条基函数占总基函数的比例增大，若此时对曲线进行小波光顺处理，过滤掉的细节曲线非均匀特性增强，则会出现失真现象。

为形象地说明曲线的细节失真现象，如图2a所示，现将某131个控制点的“W”形曲线加入距离0.5 mm范围内的噪声，即对控制点进行0.5 mm范围内的随机偏移，将曲线依次光顺到67、35、19、11、7、5、4个控制点，图2b～图2h为每次光顺过滤掉的细节，当曲线从11个控制点向7个控制点光顺时，过滤掉的细节曲线控制点范围显著超出之前过滤掉的细节，且超过0.5 mm，直至由5个控制点向4个控制点光顺时细节曲线成为直线。

图2 某“W”形曲线及其多次光顺过滤掉的细节曲线

这是由于曲线光顺过程中，其控制点越来越少，细节曲线控制点也越来越少，根据B样条曲线的定义，曲线的形状由控制顶点和B样条基函数共同决定，控制顶点减少，B样条基函数数量也随之减少，非均匀B样条基函数的数量占基函数总数的比重越来越高，曲线受非均匀B样条基函数的影响越来越大，准均匀特性减弱，细节曲线就会出现失真现象。

3.2 曲线的细节修正

本文以控制点数分别为131和259的小半圆（半径50 mm，记作R50）、大半圆（半径200 mm，记作R200）、半椭圆（长半轴50 mm，短半轴40 mm，记作T5040）以及某B样条曲线弧（记作Hu）为例，将每条曲线随机加入0.05 mm、0.1 mm以及0.5 mm范围内的噪声，即对每个控制顶点分别进行相应范围内的随机偏移，然后对每条曲线进行小波光顺处理，光顺到11个控制点，将加入的噪声计算的细节比记作理想细节比，将过滤掉的噪声计算的细节比记作实际细节比，计算实际细节比所占理想细节比的比例及其平均值，结果如表1所列，由表1可知，曲线光顺到11个控制点所过滤掉的细节部分计算的细节比约为理想细节比的97%。

表1 曲线理想细节比与实际细节比

在实际曲线重构时，为保证曲线的光顺性并且节约存储空间，同时便于工程人员操作并简化计算，曲线的控制点一般不会太多，因此将曲线光顺到11个控制点即可得到曲线大部分的细节信息，由这部分细节信息计算曲线的细节比，然后根据曲线光顺到11个控制点所过滤掉的细节部分计算的细节比约为理想细节比的97%进行修正。

4 基于细节比的曲线品质等级标定

由细节比的性质可知，曲线品质等级越低，所含的细节部分越多，细节比的值也就越大。根据这一性质，可以对不同品质的曲线进行数值标定。标定方法为：在半圆形曲线上将控制点随机移动不同范围的距离，即随机加入不同大小的噪声，然后由加入的噪声和加入噪声后的曲线计算曲线的细节比，最后由细节大小和细节比进行标定。

分别以半径为50 mm、100 mm、200 mm的半圆进行标定，为3条曲线加入0～1 mm范围内的噪声，每次增大的距离为0.01 mm，得到散点图，对这些散点进行多项式拟合，可以得到3条直线，如图3所示，其中，n为加入噪声的范围大小。

图3 曲线标定散点图拟合

由于在实际曲线重构时得到的曲线控制点数量有一定限制，所以只需将其光顺到11个控制点即可得到约97%的细节部分，因此直线的斜率和截距均变为理想直线的97%。当加入的噪声为0时，曲线的细节比也应为0，所以细节比与噪声大小是线性关系，如图4所示。

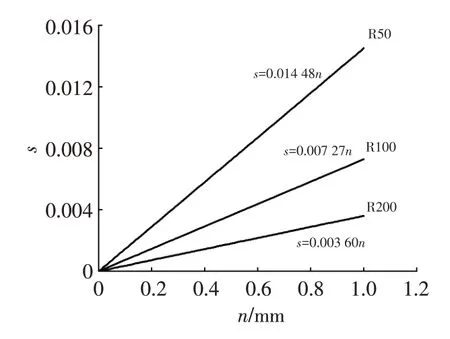
图4 曲线标定线性图

由图4可知：在噪声大小相同的情况下，外形尺寸（即曲线控制点矩阵的F范数值）越大的曲线细节比越小，曲线的品质等级越高，这与实际情况相符，外形尺寸越大的曲线，细节比图像的斜率越小；细节比相同时（即曲线的品质相同时），外形尺寸较小的曲线所含的噪声较小，在实际应用中，当两曲线品质相同时，外形尺寸较大的曲线能过滤掉的细节部分也较大，这与图4所示情况相符。

根据标定结果，按照细节比的数量级大小，可以将曲线的品质划分为8个等级，如表2所示，等级8的曲线品质最好，等级1最差。

表2 曲线等级表

在使用细节比图（s-n图）时，首先由曲线光顺后过滤掉的细节计算∑Cnoise，得到∑Cnoise的控制顶点并计算各顶点与原点的最大距离nmax，然后计算曲线的细节比s，根据点(s,nmax)在图4中的位置即可评定曲线的品质等级。

5 工程实例分析

根据曲线品质等级标定方法进行工程实例分析，以验证其可行性。

图5所示为某汽车车灯曲面点云，对曲面进行重构时，需要先进行截面曲线重构，为此，在车灯点云上截取2个截面点云进行曲线重构，得到2条品质不同的曲线，控制点数均为131个，经过平移变换后，曲线如图6所示。

图5 某汽车车灯点云

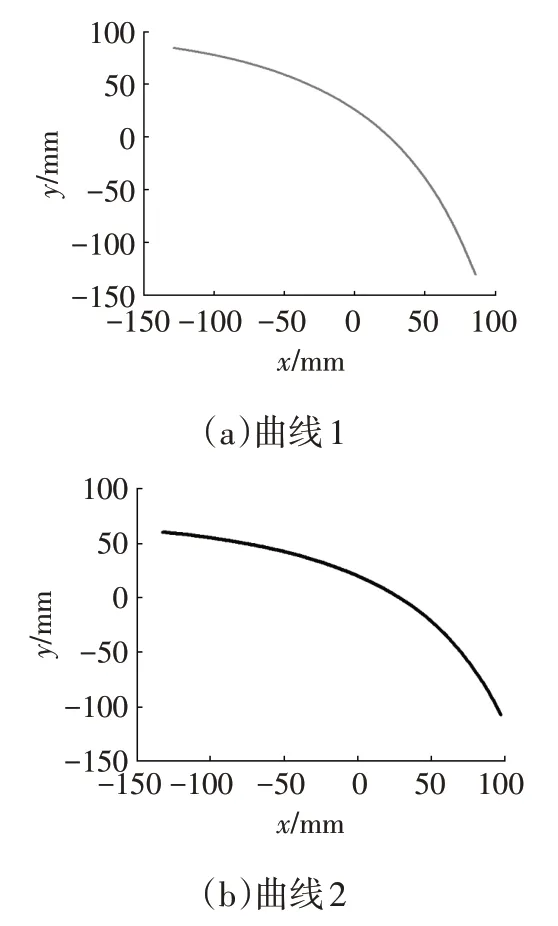
图6 汽车车灯重构曲线

由于控制点数量较多，图6难以反映二者品质上的区别，分别对其进行曲率分析，作曲率关于弧长比的关系图，结果如图7所示，由图7可以看出，曲线2的曲率较曲线1波动范围更大且变化更剧烈，曲线2的品质较曲线1差。

图7 曲线1和曲线2的曲率分析

对2条曲线分别进行光顺处理，光顺到11个控制点，得到的细节总和如图8所示，计算∑Cnoise的控制顶点中与原点的最大距离分别为nmax1=0.010 504 mm、nmax2=0.238 152 mm，故曲线2过滤掉的细节远大于曲线1。再分别计算两曲线的(∑Cnoise+∑Cscale)（记作∑C）可得∑C1=1 064.565 183、∑C2=997.253 196。

比较R100、R200、曲线1和曲线2的∑C可知，∑CR100＜∑C2＜∑C1＜∑CR200。因此，图4中曲线1和曲线2的s-n图像应处在R100和R200的s-n图像之 间，计算曲线1和曲线2的细节比可得：s1=5.623 447×10-5、s2=1.274×10-3。

根据(s1,nmax1)和(s2,nmax2)在图4中的位置，结合表2可知，曲线1为6级曲线，曲线2为3级曲线，曲线2的品质较差，为保证重构曲面的品质，需要对曲线2进行一定的处理才可用于构建曲面，这与图7所示的两曲线曲率分析结论相符，而本文方法可以进行定量分析，能够提高分析结果的准确性。

6 结束语

本文提出了一种定量评定曲线品质等级的方法，通过曲线嵌套形式的小波分解，结合得到的光顺信息和细节信息构建曲线的细节比，由细节比的性质和数值对曲线品质等级进行划分，与传统的人工通过经验评定曲线品质的方法不同，本方法给出了曲线品质等级的统一定量划分依据。通过工程实例验证，可以得到以下结论：

a.曲线光顺到含有一定数量均匀基函数时可得到大部分细节信息，其余细节信息可以通过系数修正；

b.曲线的细节比数值大小与曲线的外形尺寸（曲线控制点矩阵的F范数值）和曲线所含细节信息大小有关；

c.曲线的品质等级越高，则其细节比越小，曲线所包含的细节信息越少；

d.由于计算过程只需要进行小波分解，能够得到定量化的分析结果，消除人为因素的影响，评定方法准确、高效。