基于动态轴荷的电动汽车再生制动策略研究

李佳伟 敖银辉

（广东工业大学，广州 511400）

主题词：再生制动 制动力分配 模糊逻辑估算 动态轴荷

1 前言

电动汽车再生制动系统主要由机械摩擦制动与电机再生制动两部分组成[1]。电机再生制动是根据电机的电动机/发电机可逆性原理将车辆部分动能转化为电能储存在能量储存装置中。传统的制动力分配策略是使前轮与后轮同时抱死或前轮先抱死，以避免发生后轴侧滑。对于后轮驱动的车辆，由于采用传统制动力分配策略时后轮制动力相对较小，制动中可回收的能量相比于前轮驱动更少。Zhang Junzhi等人[2]修改了传统的β曲线，使其更好地逼近理想的制动力分配曲线，为后驱车辆提供更强的能量再生能力。Mehrdad Ehsani[3]进行了再生制动系统与ABS之间协调工作的研究。Hayashida等[4]将动力电池和超级电容组合为能量供给及回收系统，更有效地回收制动能量。Gao Yimin[5-6]和Hoon Yeo[7]分别提出了各自的前、后轮制动力分配模型，并进行了再生制动系统的设计。Panagiotidis与Delagrammatikas等以并联式混合动力电动汽车为研究对象建立了再生制动系统模型,并进行了仿真分析,对再生制动系统的制动作用以及能量回收的影响因素进行了系统分析[8]。

在上述方法中，研究者所提出的制动力分配策略都是按固定的前、后轴荷比例分配制动力，没有考虑在实际制动或加速过程中悬架的非线性变形造成前、后轴载荷的转移。为此，本文提出一种基于动态轴荷的制动力分配策略，建立以制动强度、车速和电池荷电状态（State Of Charge，SOC）作为输入变量，期望的再生制动力作为输出变量的模糊逻辑控制模型，并在ADVISOR中进行仿真验证。

2 车辆动力学分析

本文从再生制动效率的角度考虑了悬架非线性变形对再生制动系统的影响，建立了7自由度整车模型，如图1所示。

图1 7自由度汽车悬架非线性几何简化模型

非线性弹簧的弹性-位移方程为：

式中，F1为弹簧弹力；k1为弹簧刚度系数；τ为弹簧的非线性系数；xi(i=1,2)为弹簧第i段位移。

根据式（1），车辆行驶时的悬架力为：

式中，Fsf、Fsr分别为前、后轴的悬架力；yc为簧载质量位移；a、b分别为汽车质心到前、后轴中心线的距离；θ为制动时的俯仰角；kf、kr分别为前、后悬架的弹簧刚度；yf、yr分别为前、后悬架的非簧载质量位移；cf、cr分别为前、后悬架的阻尼系数。

簧载质量运动方程为：

式中，mc为簧载质量；Jc为簧载质量的俯仰转动惯量；hg为汽车质心高度。

非簧载质量运动方程为：

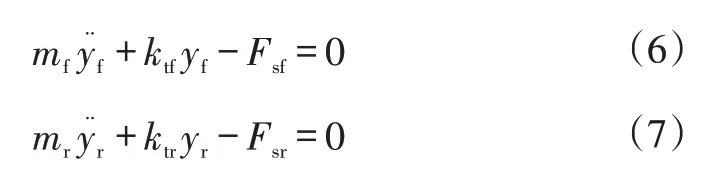
式中，mf、mr分别为前、后悬架非簧载质量；ktf、ktr分别为前、后轮的垂直刚度。

图2所示为车轮受力情况，车轮的运动方程为：

式中，Jf、Jr分别为前、后轮的转动惯量；ωf、ωr分别为前、后轮的角速度；Fxf、Fxr分别为来自地面的前轮和后轮的制动力；Rf、Rr分别为前、后轮的滚动半径；Tf、Tr分别为制动时前、后轮上的制动力矩；Treb为电机提供的转矩。

图2 车轮受力分析

车轮在地面上的垂直载荷为：

式中，Fzf、Fzr分别为前、后轴地面法向反作用力；L为轴距；g为重力加速度。

汽车的纵向动力学方程为：

式中，Ff为轮胎滚动阻力；Fw为空气阻力；f1、f2为滚动阻力系数；m为汽车总质量；CD为空气阻力系数；A为车辆的迎风面积；u为车速。

3 再生制动策略

3.1 理想制动力分配策略

再生制动系统的结构可依据电动机和摩擦制动系统协调工作的方式分为串联和并联两类。本文的研究对象采用串联结构，电动机和摩擦制动力可以单独控制。针对不同情况，传统再生制动分配策略主要包括理想制动力分配策略、并行制动力分配策略和最佳能量回收分配策略等。

理想再生制动力分配策略基于线性车辆模型，不考虑悬架变形：

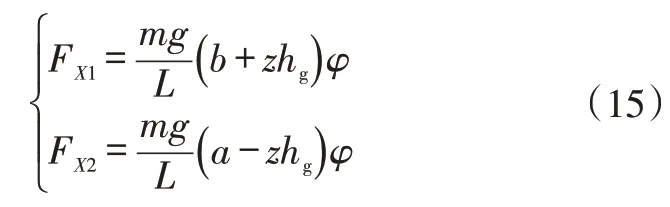
式中，FX1、FX2分别为前、后车轮制动力；z为制动强度；φ为轮胎与路面间的附着系数。

实际制动或加速过程中，悬架的非线性变形会造成前、后轴载荷的转移，其程度受制动强度的影响。由于理想制动力分配策略依据前、后轴荷比例分配制动力，因此轴荷变化时前、后制动力分配也会发生变化：

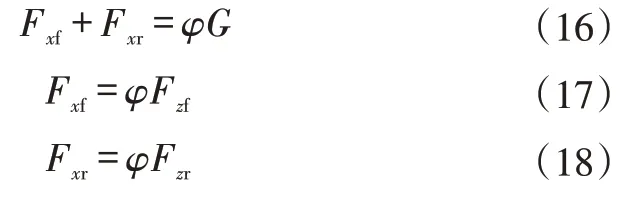
式中，G为整车重力。

3.2 基于动态轴荷的制动力分配策略

本文采用基于动态轴荷的制动力分配策略：通过位移传感器测量前、后悬架的非簧载质量位移yf、yr，由式（10）、式（11）计算出前、后轴载荷，然后根据实时的前、后轴载荷Fzf、Fzr与模糊逻辑估计的附着系数φ来确定前、后轮制动力分配系数。

车辆在行驶时有加速、匀速、减速（制动）3种工况，而加速与减速都会引起悬架的变形，当且仅当车辆处在制动工况下，位移传感器检测的前、后悬架非簧载质量位移是有效的。

为了在保证安全的情况下尽可能多地回收能量，将制动按强度分为3种，即紧急制动、中等制动和轻制动。当车辆处于紧急制动工况时，制动强度很快达到甚至超过0.8，此时制动力完全由机械制动力提供；当制动强度小于0.1时，车辆处于轻制动工况，制动力完全由驱动轮（前轮）提供，后轮制动力为零，此时制动回收能量最多。当制动强度大于0.1时，前、后轮制动力按式（17）、式（18）进行分配。制动力计算分配过程如图3所示。

图3 基于动态轴荷的制动力分配流程

4 基于动态轴荷的制动力模糊控制策略

4.1 模糊控制结构

电动车再生制动时的制动力分配受很多因素影响，且很多参数实时变化。由于模糊控制策略适用于被控对象的数学模型不精确的情况且具有鲁棒性强等优点，因此将模糊控制理论应用于纯电动汽车再生制动系统制动力分配中。

本文采用双模糊控制结构，如图4所示，其中Fbf、Fbr分别为前、后轴制动力，K为再生制动力系数，Fmf为前轴机械制动力，由摩擦制动器提供，Freg为前轴再生制动力，由电机提供。

图4 模糊控制结构

4.2 基于模糊逻辑的附着系数估算

轮胎与路面间附着系数的估算中，基于轮胎模型的估算方法一直占据主导地位。其对车辆动态运动状态进行测量，例如车轮转速和车辆加速度。由于轮胎模型法所需要测量的数据较多，计算相对复杂，要实现实时的φ值估算较为困难。因此，本文提出一种基于模糊逻辑的附着系数估计方法，不依赖于任何具体的轮胎模型，只需要对车轮滑移率进行估计。

车辆制动时，车轮中心速度vw大于车轮轮边线速度vb，轮胎与地面会产生相对滑动。随着制动强度的增加，滑动成分占比越来越大。一般用滑动率S表示滑动成分的占比：

式中，Re为车轮滚动半径；ωw为车轮角速度。

由式（19）可知，汽车的滑移率由车速和轮速决定。本文使用卡尔曼滤波算法估算车辆的滑移率，该算法是使用车辆系统模型当前时刻的状态测量信息以及前一时刻的车辆状态估计信息，通过递推公式获得目前时刻所估计状态的值，可以极大地提高计算效率，在实际应用中更加方便、简单，易于实现。

车轮在车辆空载时半径为R0，在实际运动过程中，受路面和环境因素影响，Re不断变化。对于两驱车，从动轮的滑移率较小，因此以由从动轮处获取的车身速度为研究对象，用车轮变形系数ϵ来表示从动轮滚动时的受压情况：

则车速为：

式中，ωe为从动轮角速度；ve为从动轮轮速。

根据卡尔曼滤波算法，可得：

式中，A、B、H为系数矩阵；at为车辆的加速度；am为测量加速度；na为加速度测量噪声；vme为车速测量值；nv为车速测量噪声；w1、w2、w3为系统噪声。

经过卡尔曼滤波后，得到车轮速度ve和车轮变形系数ϵ。由式（21）得出车速vw，车轮角速度ωw可测量获得，再通过式（19）便可实时估算车轮的滑移率。

附着系数φ与滑移率S的关系曲线如图5所示，从图5中可以看出，当滑移率位于ε段时，附着系数达到最大值，之后随着滑移率的增大，附着系数逐渐减小。

图5 附着系数-滑移率曲线

本文所提出的最佳附着系数估算方法是为了最大限度地利用路面-轮胎附着力，使前轮或后轮制动力接近抱死极限。

本文以车轮滑移率S为输入变量，采用Mamdani型模糊控制器实现附着系数的变化量Δφ的控制。

滑移率S、附着系数变化量Δφ的模糊子集均为{L（低）,M（中）,H（高）}，域范围分别为[0,0.3]、[-0.2,0.2]，隶属函数如图6、图7所示。

将一段时间内的减速需求离散化，并将其划分为固定持续时间的n个时间步长，φ的估计值为：

式中，p为时间样本；φei为当前时间步长的估计值；φ0i为前一时间步长的估计值；Δφp为当前时间步长中的估计值的变化；i为在连续的时间步骤中连续要求减速的次数。

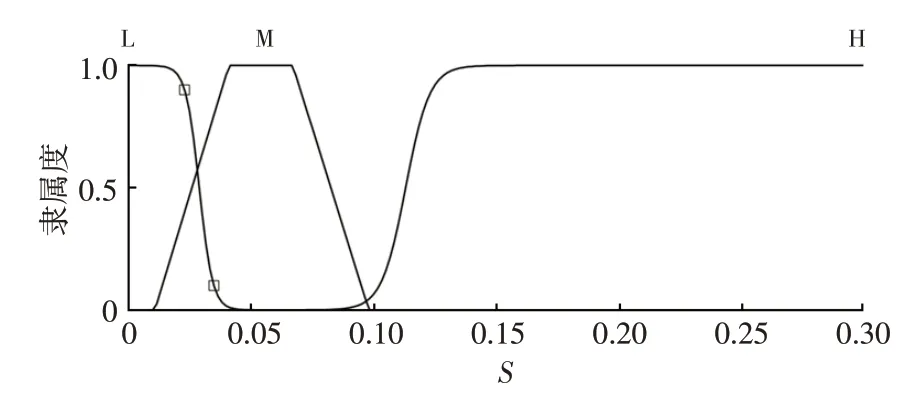
图6 滑移率S的隶属函数

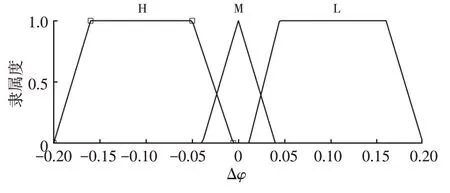
图7 附着系数变化量Δφ隶属函数

在制动过程中，先前的减速样本的估计值φe,i-1保留为初始的φ估计，并将其作为后续制动期间的φ估计。在每个制动事件结束时，φ估计都将停止。

4.3 基于模糊逻辑的再生制动系数估算

再生制动系数模糊控制器采用三输入单输出的结构，输入变量分别为电池SOC、车速v和制动强度z，输出为前轴再生制动力占前轴总制动力的比例K。

该模糊控制器的输入量模糊子集为：车速E(v)={L,M,H}，域范围为[0,100]km/h，制动强度E(z)={L,M,H}，域范围为[0,1]，荷电状态E(SOC)={L,M,H}，域范围为[0,100%]。输出变量再生制动系数的模糊子集E(k)={L,M,H}，域范围为[0,1]，隶属函数如图8所示。

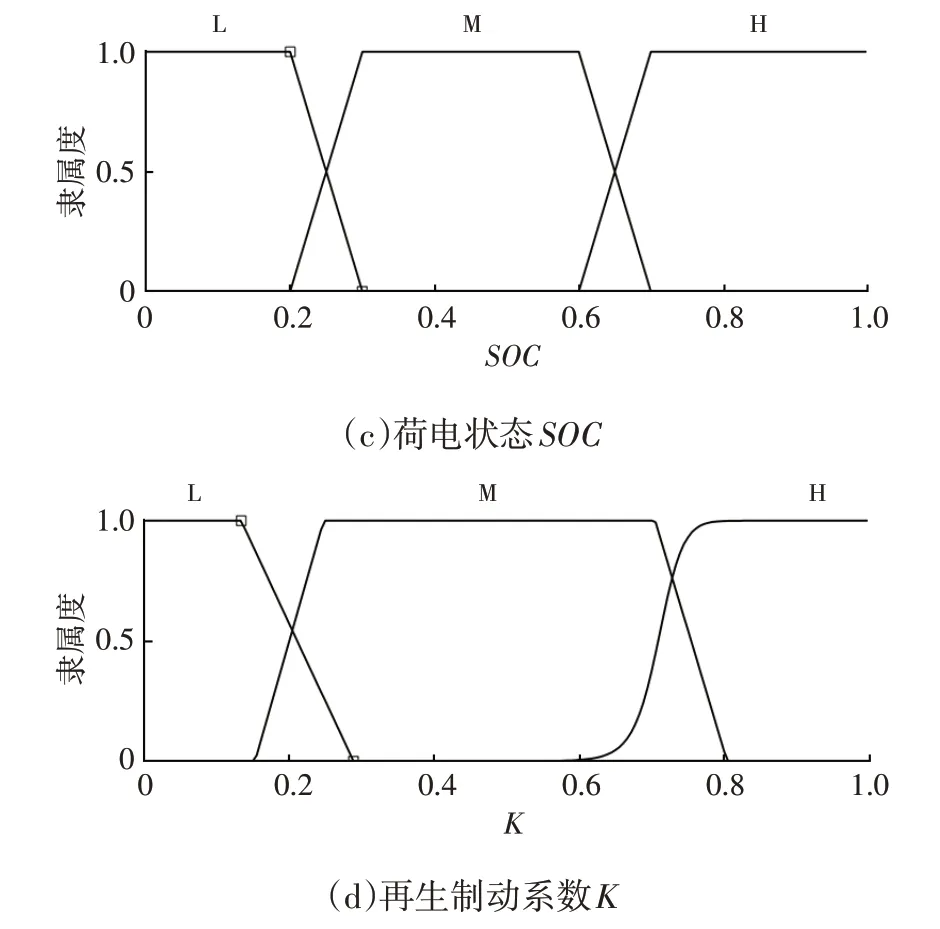
图8 隶属函数

通过模糊控制器得到车速v、制动强度z、电池SOC以及再生制动系数K之间的关系如图9所示。

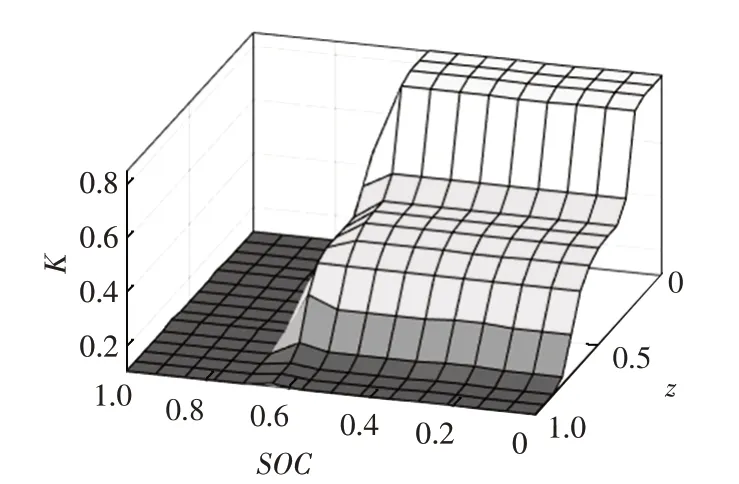
图9 再生制动系数随速度、制动强度、SOC的变化曲线

5 仿真结果与分析

5.1 仿真模型的搭建

根据本文所提出的再生制动控制策略，在MATLAB/Simulink环境下搭建基于模糊控制的再生制动模型。为了确保仿真结果的准确性，本文搭建了前向仿真模型和后向仿真模型，如图10、图11所示。而在进行电动汽车的仿真计算时，采用ADVISOR中的混合仿真方法，即以后向仿真为主，前向仿真为辅。

图10和图11中的模糊逻辑控制策略模型如图12所示，前、后轴制动力分配子模块模型如图13所示。

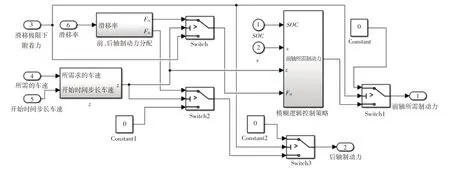
图11 后向路径模糊控制制动力分配模型

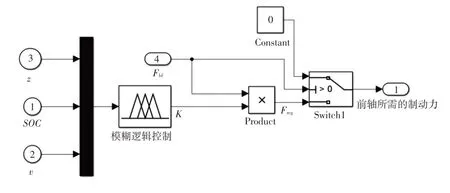
图12 模糊逻辑控制策略模型

5.2 仿真参数和工况的设置

本文仿真中的纯电动汽车相关参数如表1所示。仿真中采用美国城市道路循环工况CYC_UDDS，循环工况基本参数如表2所示。

5.3 仿真结果与分析

把该模型嵌入到ADVISOR2002仿真环境中，并在CYC_UDDS循环工况下验证模型在电动汽车再生制动系统中的效果。运行ADVISOR2002后，将自带的控制策略与本文提出的改进策略进行对比，结果如图14所示。在CYC_UDDS循环工况下汽车制动过程中前、后悬架非簧载质量位移如图15所示。由图14可以看出，在CYC_UDDS循环工况结束时，采用本文提出的基于动态轴荷的纯电动车再生制动策略时电池SOC减少26%，采用ADVISOR自带控制策略时电池SOC减少28%，对比SOC提高7.1%，且改进的控制策略电池SOC下降相对缓慢，提高了纯电动汽车的续航里程。

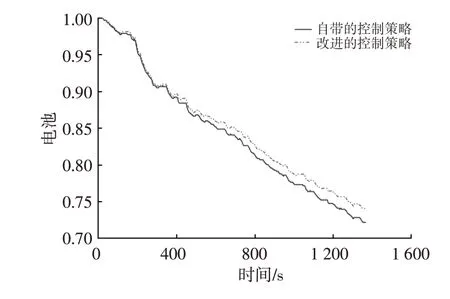
图14 SOC对比曲线模型

图15 前、后悬架非簧载质量位移

6 结束语

本文通过对再生制动的研究，针对现有制动策略的不足，考虑到汽车制动时悬架非线性位移造成的轴荷转移，结合模糊逻辑控制提出一种基于动态轴荷的纯电动汽车再生制动策略。利用ADVISOR仿真软件将软件自带的控制策略与本文所提出的控制策略进行对比分析，结果表明，在CYC_UDDS循环工况下，本文提出的基于动态轴荷的纯电动车再生制动策略SOC较ADVISOR自带的控制策略剩余SOC提高7.1%，表明本文提出的控制策略能够有效提高续驶里程。