基于反步法的多机械臂系统力/位混合控制
(青岛大学 自动化学院,青岛 266071)
自从20世纪60年代将机器人引入工业生产以来,制造工业取得了很大的进步。如今,机器人的应用逐步拓展到制造业、农业和工业等众多领域。目前国内工业生产中多数使用单臂机器人[1-2],但单臂机器人在组装零件、搬运重物等工业生产活动中效率低下,难以达到预期的要求。协同机器人[3]是多个机械臂共同完成生产活动,因此协同机器人在协调性和灵活性上都要优于单臂机器人。随着科技的进步,协同机器人领域也在不断的创新与发展,比如丹麦公司Universal Robots在2015年推出的机器人UR3便具有重量轻、高智能、易安装等优点。
相比于单机械臂系统,多机械臂系统的控制问题更为困难。当多个机械臂在搬运同一物体时,首先,要保证物体按照期望的轨迹运动。此时每个机械臂的末端执行器需要与物体的运动轨迹保持一致,这就导致末端执行器在运动的速度和位置上都会受到约束。其次,末端执行器与物体之间的接触力等内力也需要控制,以确保机械臂可以抓牢物体的同时不损坏物体。所以,在考虑位置控制的同时也应该考虑内力控制。因此如何实现机械臂的力/位混合控制[4]成为当前机械化工业面临的主要困难之一[5]。
机械臂系统是一个高阶强耦合的非线性系统,因此,专家们在对有未建模动态的多机械臂系统的控制问题上进行了大量的研究。文献[6]在多机械臂系统中引入了一种新的综合动力学模型,并为这些系统的位置和力跟踪问题设计分散自适应协同控制器。文献[7]开发了一种滑模控制方法,用于解决不确定协同机器人的控制问题。然而这些方法在控制器的设计上都比较复杂,本文运用反步控制[8]方法简化控制器的设计。反步法是一种可以高效地处理系统中存在的非线性项的控制方法,其基本思想是将复杂的非线性系统分解成一系列单个子系统,接着在每一个子系统中引入虚拟控制函数,并且选择适当的Lyapunov函数以完成整个控制器的设计[9]。
综上所述,本文针对具有未建模动态和未知外部扰动的多机械臂系统提出一种基于模糊反步法的力/位混合控制方法,并使用Matlab软件进行了仿真。与传统的方法相比,本文的主要创新点如下:
(1)研究了多机械臂的力/位混合控制问题,并使用反步法简化了控制器的设计过程;
(2)使用自适应模糊方法处理机械臂系统存在的高度非线性和未知扰动的问题。
1 多机械臂系统空间模型
图1所示为机械臂共同控制一个物体的模型图,并且在图中建立了相对应的坐标系以便导出整个系统的动态模型。{B}表示参考坐标系,{O}表示以刚性物体的质心为原点建立的坐标系,{Ei}(1≤i≤k)表示以第i个末端执行器为原点建立的坐标系。
为了简化整个系统数学模型,提出以下假设[10-13]:
假设1:机械臂自由度相同;
假设2:物体与所有末端执行器的接触是刚性的;
假设3:每个机械臂的运动远离奇点;
假设4:所有关节和被抓物体都是刚性的。
2 多机械臂系统数学模型
2.1 机械臂的动力学模型
第i个机械臂的动力学方程为[14]

由式(1)可得k个机械臂的动力学方程是:
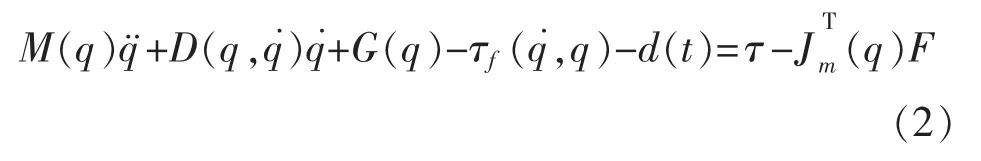
式中:


假设 5:di(t)满足‖di(t)‖≤,其中是一个未知正常数。
由假设 3 可知,Jacobian 矩阵 Jm,i(qi)可由第 i个机械臂的正向动力学得到,如式(3)所示:


2.2 物体的动态模型
物体的动态方程为[15-16]
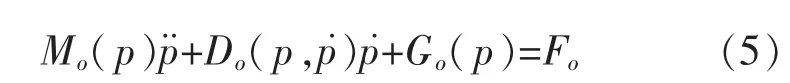
式中: p∈R2是物体的位置向量;Mo(p)∈R2×2表示物体的质量矩阵;Do( p,p˙)∈R2×2表示科里奥利力-离心力矩阵;Go(p)∈R2表示重力矢量;Fo是物体的合力矩矢量;可以表示为

式中:Jo,ei( p)∈R2×2表示第 i个末端执行器到物体的Jacobian矩阵,由此可得:

F由内力f和外力E两部分组成,可得:

式中

将式(8)带入式(7)可得:


假设6:物体的运动不会受到内力的影响,内力之间可以互相抵消,也就是说:
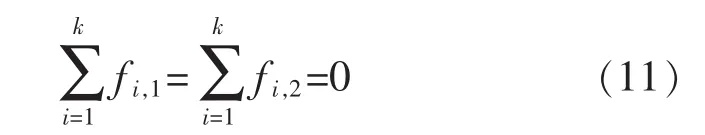
2.3 多机械臂配合动力学模型
基于假设3,物体的位置和方向向量矩阵p可以用关节向量qi表示:

对式(8)求导可得:


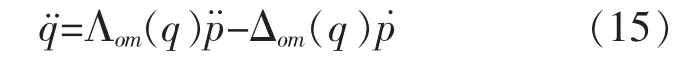
将式(10)、式(14)和式(15)带入式(2)中可得多机械臂协作的动力学模型:

式中:

定义新的变量如下:

则式(16)可以表示为
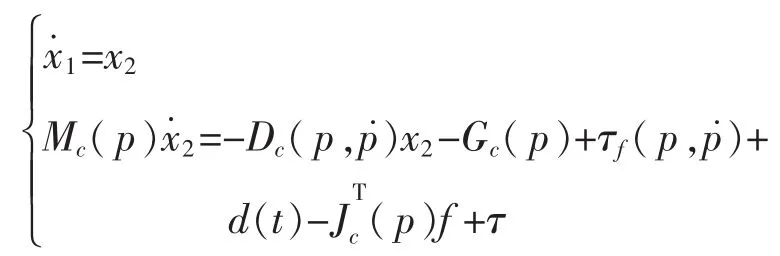
3 控制器设计
步骤1定义系统误差变量如下:

式中:x1d为期望的物体运动轨迹;α为虚拟控制信号。
选取李雅普诺夫函数为

对式(18)求导,可得:

选取虚拟控制律 α=-k1z1+,则

步骤2选取Lyapunov函数
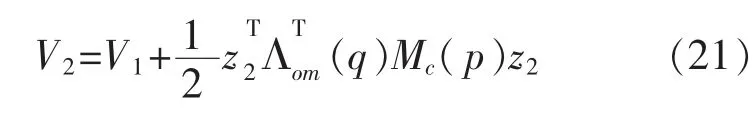
对式(21)求导可得:

由式(22)可得:


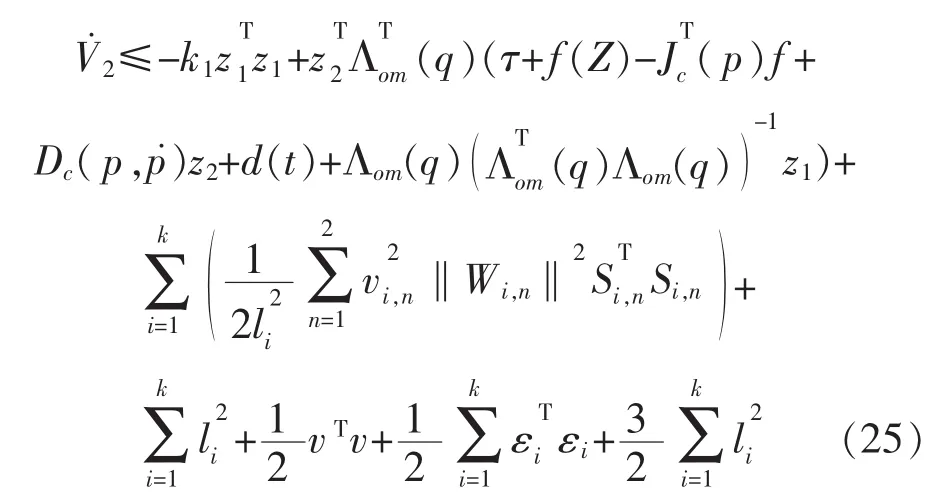
基于假设5和杨氏不等式,可得:

令 ef=f0-f,f0是期望的内力,ef是内力误差,令选取真实控制律:

式中:σf,d,σf,i是正常数;为 θi的估计值,θi将在后文定义。 将式(27)带入式(26)中得到:

比较式(4)、式(7)和式(11),可得:
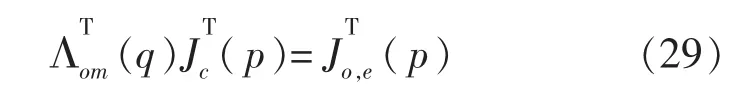
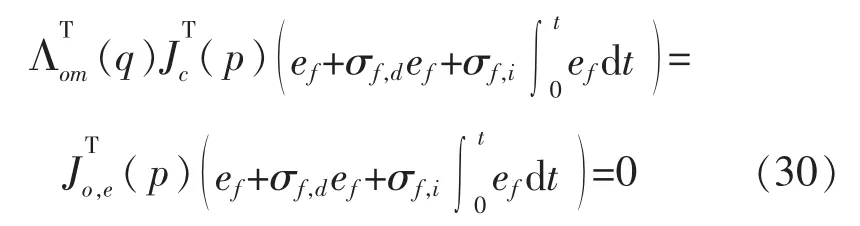
将式(30)带入式(28)可得:

步骤 3令,选取 Lyapunov 函数:
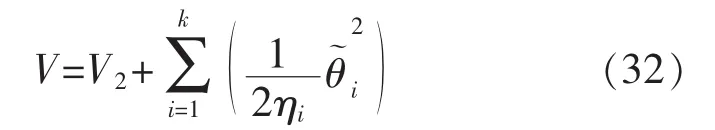
对式(32)求导可得:
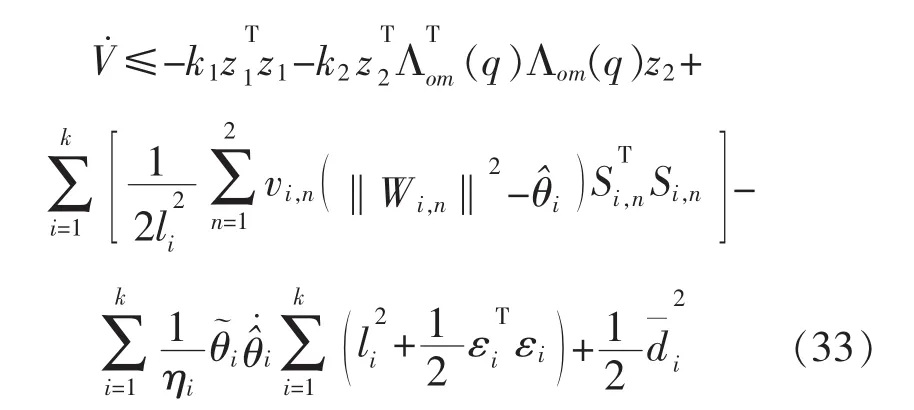


定义自适应律:

式中:ηi>0,mi>0。
4 稳定性分析
将式(35)带入式(34)中可得:

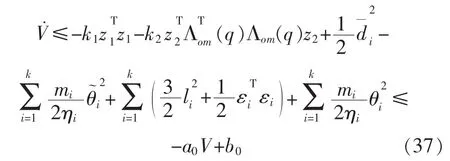

由式(31)容易得到:

显然有:
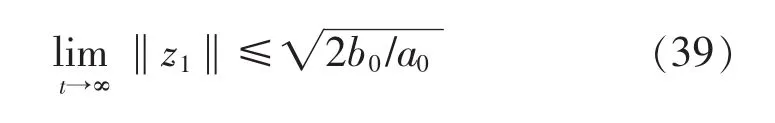
将τ带入式(16)中可得:
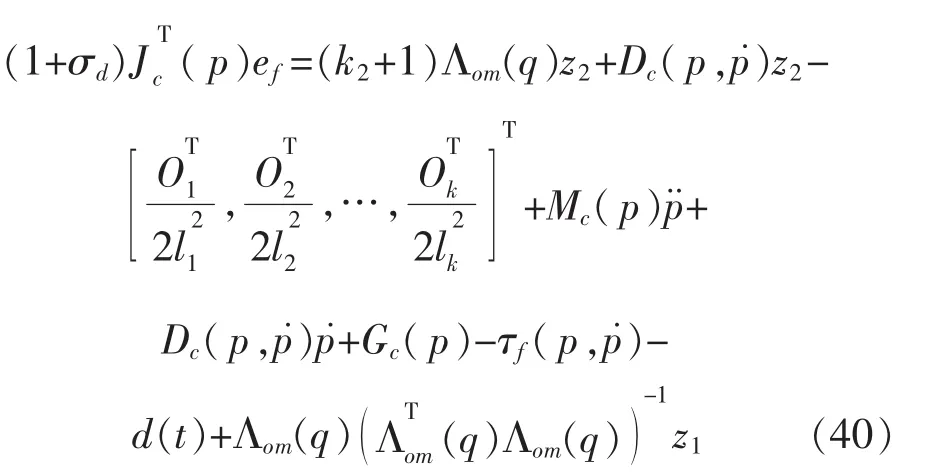
由于系统内的信号都是有界的,所以只要σd的取值合适,内力误差就会收敛到一个极小的值。
由上述分析可得以下结论:
假设x1d为期望跟踪信号,结合模糊自适应逼近理论、虚拟控制律α和自适应律θ的共同作用下,位置跟踪误差将会收敛到原点周围极小的邻域内,并且选取合适的 σf,d,σf,i,使内力的误差收敛到原点周围极小的邻域内。
5 系统仿真结果
为了验证所提出的基于自适应模糊的反步控制方案的有效性,本文在Matlab环境中进行了仿真,如图2所示,这两个二连杆平面机械臂共同抓取一个球形物体。是机械臂每一个关节的角度,每个机械臂的动力学方程由式(1)表示,其中 Mi(qi),Gi(qi),Di(qi,)在文献[18]中给出。 di(t),τf,i(qi,)由式(41)和式(42)得到:


图2 双机械臂模型Fig.2 Two two-link planar manipulators model
机械臂的长度分别是:l1,1=l2,1=1 m,l1,2=l2,2=1 m;
质量分别是:m1,1=m2,1=1 kg,m1,2=m2,2=1 kg;
转动惯量分别是:I1,1=I2,1=1.5 N·m2,I1,2=I2,2=0.5 N·m2;
物体的半径、质量、转动惯量分别是:l0=0.2 m,m0=0.3 kg,I0=0.1 N·m2。
机械臂的基座分别是:(x1,y1)=(-1.4,0),(x2,y2)=(1.4,0)。
在式(2)中给出了物体的动态方程,其中 M0(p)=重力加速度 g=9.8 m/s2,其中 Jeoi( p),Joq(q˙)在文献[18]中给出。
选择模糊集如下:

选择控制律参数:k1=100,k2=8,li=20,mi=20,σf,d=0.1,σf,i=20。
f0=为物体期望的位置,选取如下所示:

图3是目标物体的位置跟踪图,图4和图5分别是采用本文控制方法后物体沿X,Y轴方向上位置跟踪误差的仿真图,图6~图9是系统内力误差ef的仿真图。图10是真实控制率τ的仿真图。从图3~图5看出物体能够有效的跟踪期望的位置,图6~图9看出系统的内力误差可以收敛到原点周围极小的邻域内。

图3 物体的位置跟踪图示Fig.3 Position tracking of the object

图4 X轴跟踪误差图示Fig.4 Tracking error on X-axis

图5 Y轴跟踪误差图示Fig.5 Tracking error on Y-axis

图6 内力误差ef11图示Fig.6 Internal force erroref11

图7 内力误差ef12图示Fig.7 Internal force erroref12

图8 内力误差ef21图示Fig.8 Internal force erroref21

图9 内力误差ef22图示Fig.9 Internal force erroref22
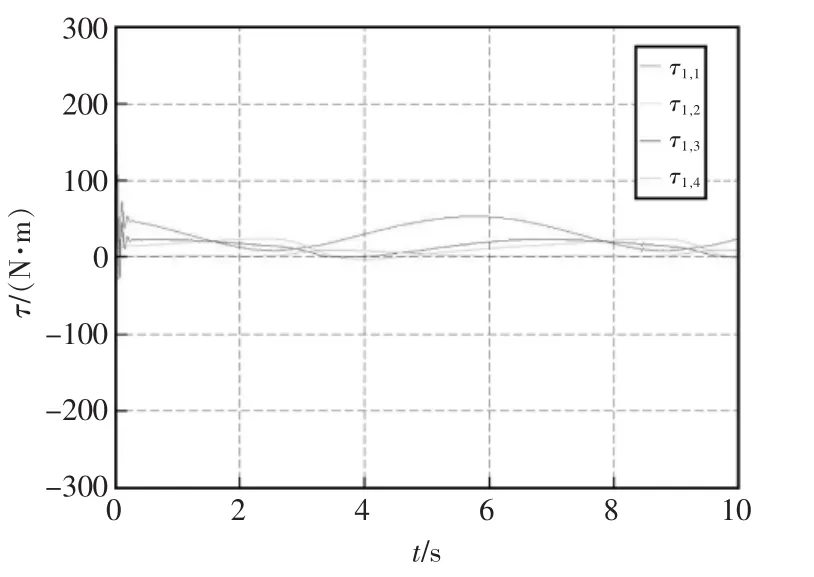
图10 控制器τ图示Fig.10 Controller τ
6 结语
本文针对多机械臂系统的未建模动态及未知扰动,采用模糊自适应控制结合反步法实现了多机械臂的力/位混合控制。仿真结果表明,设计的基于模糊自适应的控制器能够使物体有效跟踪期望的位置,且机械臂系统的内力可以控制在一个理想的范围内。

