无人艇直驱式电液伺服舵机系统建模与仿真
祝 川,卢 俊,吴 翔
(上海大学机电工程与自动化学院,上海 200444)
0 引 言
近年来喷水推进已成为高性能船舶推进方式的主体[1-2],水面无人艇也多采用这种推进方式。用于船舶航向控制的电动液压舵机系统对于改变或保持船舶航向有着至关重要的作用,主要实现两大功能,船舶直线航行受外力偏航后恢复直线运动的航向稳定性和及时改变船舶运动方向的回转性,统称为船舶的操纵性[2]。在电动液压系统中,直驱式电液伺服系统因结构简单、能源效率高的特点[3]而特别适用于无人艇的操舵控制。喷水推进无人艇能够拥有灵活的操纵性必然要求其操控转向的直驱式电液伺服舵机系统具有优良特性,这不仅仅体现在优异的硬件上,也需稳定可靠的控制算法来支持。
为保证直驱式电液伺服舵机系统拥有优良性能,对系统进行深入分析和研究,细化每个组件的作用机理,构建数学模型,搭建整体系统仿真环境,简化现场的试验工作。
1 无人艇直驱式电液伺服舵机系统建模
无人艇采用的直驱式电液伺服舵机系统,由伺服电机、液压系统、操舵机构部分组成,并承受喷水负载,如图1 所示。
1.1 伺服电机及液压系统建模
1.1.1 伺服电机建模
伺服调速电机系统可忽略电机电气控制的动态过程,简化为时滞环节。对于电机拖动的过程,简化为一阶惯性环节[4],有
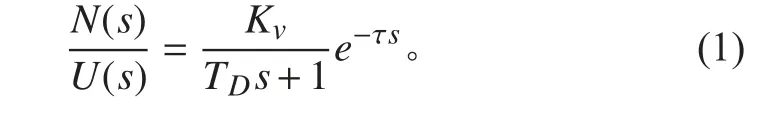
式中:U(s)为控制指令;N(s)为输出转速;Kv为速度增益;TD为电气时间常数;τ 为时滞时间。
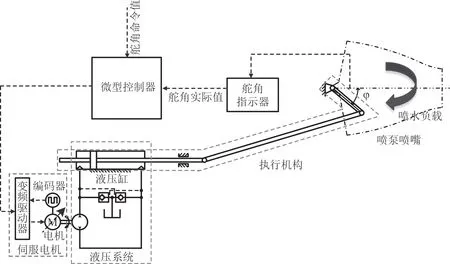
图 1 直驱式电液伺服船舶舵机系统简图Fig.1 Diagram of the marine direct-drive electro-hydraulic servo steering-gear system
1.1.2 液压系统建模
如图2 所示,舵机的液压系统主要由双向定量液压泵、对称液压缸、以及辅助的液控单向阀和小油罐组成。
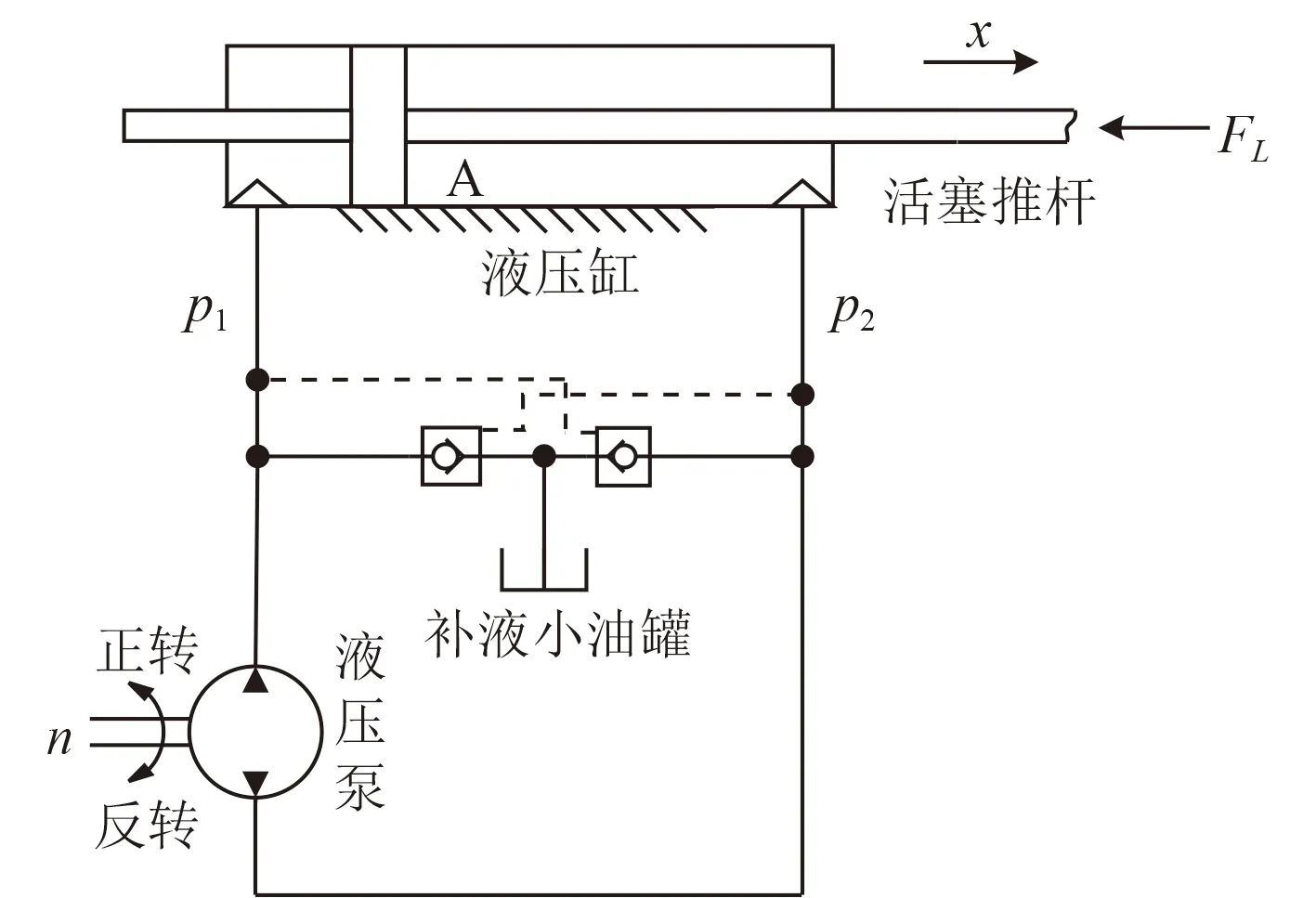
图 2 液压系统结构图Fig.2 Structure diagram of the hydraulic system
1)双向定量液压泵建模
由流体的连续性方程,可得液压泵的流量与转速的关系为:
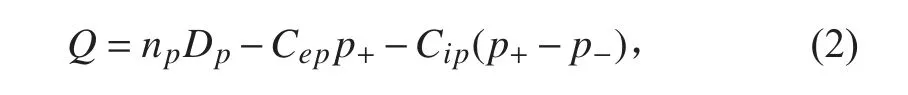
式中:Q 为流量;np为转速;Dp为排量;Cep为外泄漏系数;p+为出油口压力;p-为进油口压力;Cip为内泄漏系数。进油口压力p-相对于出油口压力p+数值非常小,将进油口压力p-设为0 Pa[5]。
2)对称液压缸建模
直驱式电液伺服系统的油管回路很短,忽略其动态特性。根据可压流体的连续性方程,有

式中:x 为活塞杆位移;V(x)为进油回路油液有效体积;βe为油液体积弹性模量;Ctm为总内外泄漏系数;A 为活塞上有效面积。
忽略液压缸与活塞杆的摩擦,活塞杆的动力学方程为:
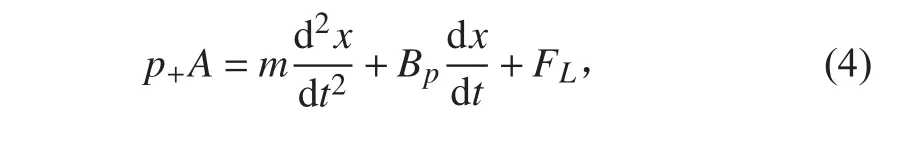
式中:m 为活塞杆质量;Bp为油液粘性阻尼系数;FL为负载力。
3)液压系统模型整合
对式(2)、式(3)和式(4)拉氏变换,消除中间变量P+(s),有

式中:ωn为液压系统的固有频率;ζ 为阻尼比系数;Ct为总泄漏系数, Ct=Ctm+Cep+Cip。
1.2 偏置滑块-曲柄的映射关系
液压活塞杆的输出为直线运动,而喷嘴舵角的需求为回转运动,实现该转换为操舵执行机构,简化为平面偏置滑块-曲柄连杆机构。
1.2.1 建立运动学和动力学方程
对平面偏置滑块-曲柄机构,忽略重力,以曲柄1 的回转中心A 为原点,以喷嘴中心线为x 轴,建立如图3所示右手坐标系xAy。
图中,l1,l2为曲柄1 和连杆2 的轴向长度;lS2为连杆质心S2到B 点的距离;l3为转动副C 点距A 点的水平距离,le为等效滑块3 的偏心距;θ1,θ2为曲柄1 和连杆2 与x 轴夹角,逆时针为正,其中,θ1与实际舵角有φ 差值;θ3,θe为矢量和与x 轴夹角;v3为滑块3 的速度,x 轴负方向为正。
建立该滑块-曲柄机构的闭环矢量图,如图4 所示。
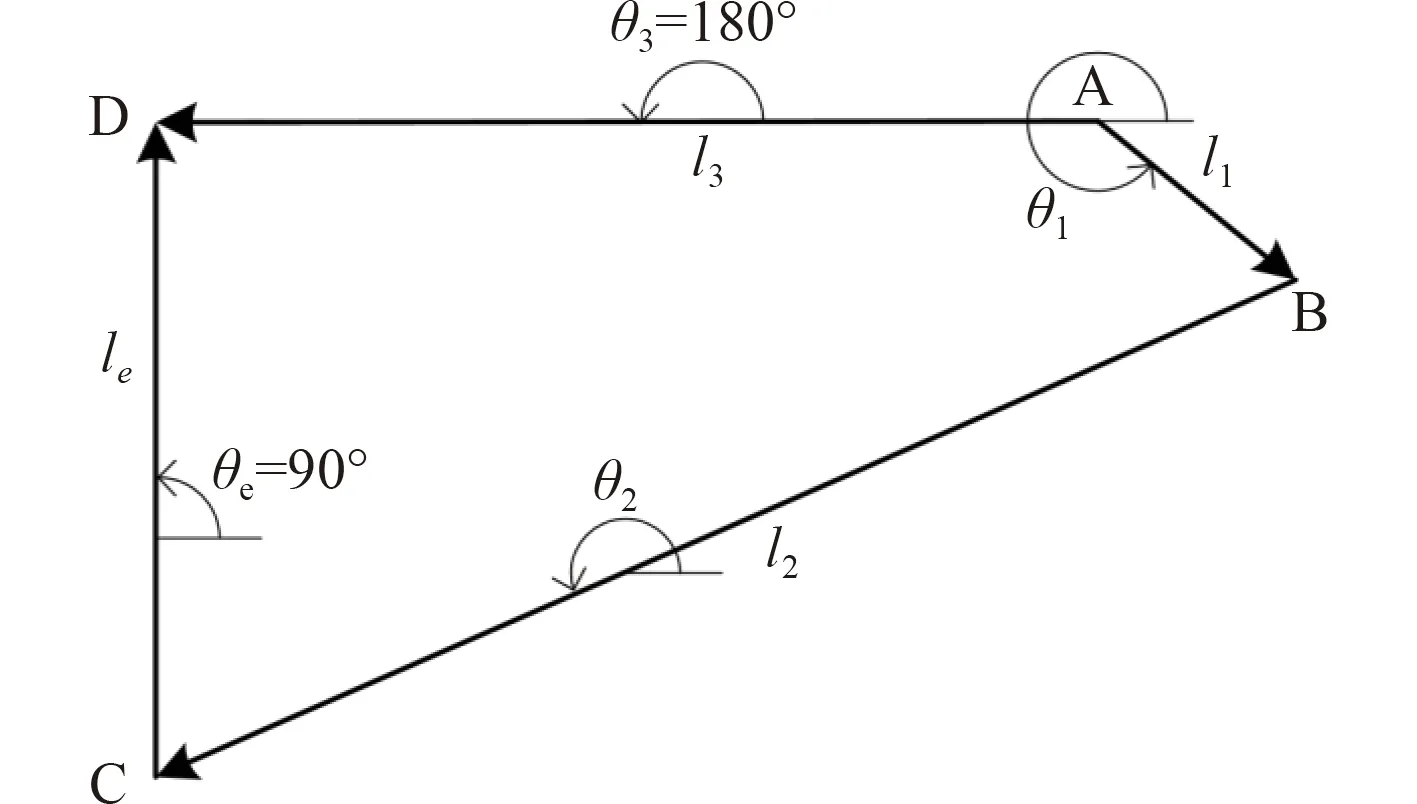
图 4 平面偏置滑块-曲柄机构组成的闭环矢量图Fig.4 Close-loop vectorgraph of planar offset crank-slider mechanism
1)运动学方程
根据图4 所示的闭环矢量图,其闭环矢量方程式为:
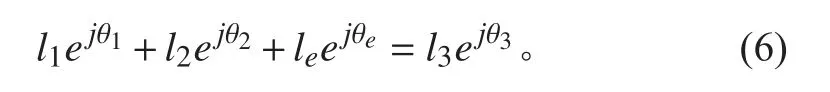
将上式向x 轴、y 轴分解,并代入固定值,有位置约束方程:
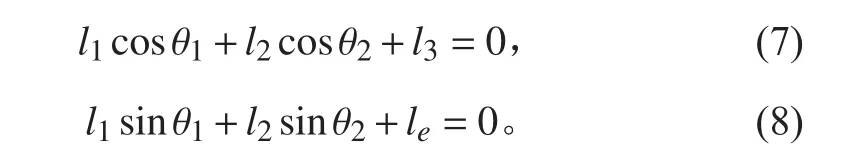
对式(7)和式(8)关于时间求导,有速度约束方程:
再对式(9)和式(10)关于时间求导,有加速度约束方程:
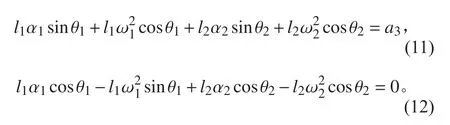
其中:α1,α2为曲柄1 和连杆2 的角加速度;a3为滑块3 的加速度。
在传统的运动学分析中,求解某时刻四连杆机构中各个构件的角速度或速度是在确定每个构件的位置和角度后进行的[6]。假定t 时刻各构件位置已知,由速度约束关系计算各构件的速度,求导为加速度。从t 到t+1 时刻,可认为在该步长内各连杆的角速度和滑块的速度相对没有变化,并在各连杆角度已知的基础上,再对每个连杆的角速度积分,可得t+1 时刻各连杆的角度,进而可求解下时刻各构件速度。
上述分析中,假定各构件的速度和角速度在分析步长内是未变的,这与真实的情况有微小的偏差。各构件初始条件也可能是互相不兼容的,引发后续迭代运算混乱。因而,需验证构件积分后的位置满足该机构闭环矢量方程的程度来衡量迭代的有效性,规定误差变量如下:

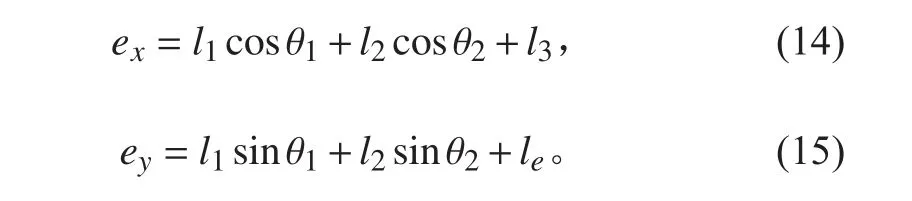
2)建立动力学方程
对每个构件进行受力分析,如图5 所示。
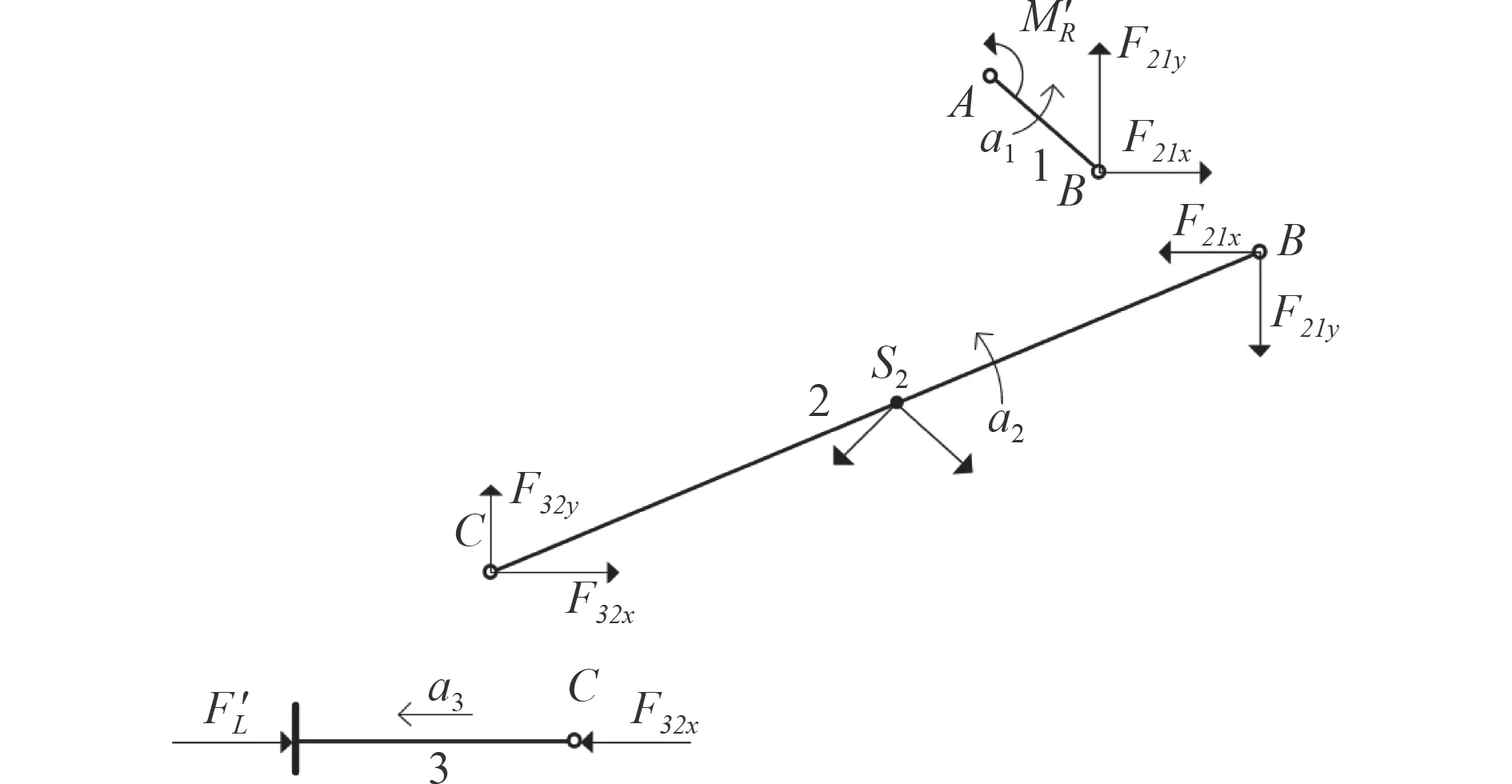
图 5 滑块-曲柄机构受力分析图Fig.5 Stress analysis diagram of crank-slider mechanism
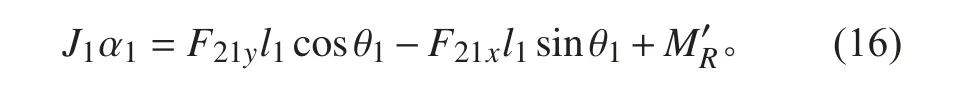
式中:J1为曲柄1 绕A 点的转动惯量;F21x,F21y为连杆2 对曲柄1 沿x 轴和y 轴的分力。
对连杆2,处于非惯性系,可先求解出其质心位置,有
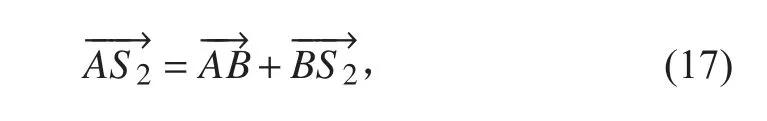
将其分解到x 轴和y 轴上,有
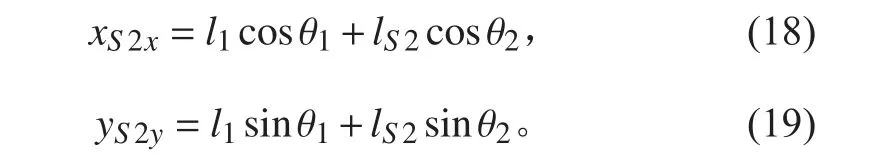
对式(18)和式(19)关于时间t 求2 阶导数,连杆2 质心的加速度关系式为:
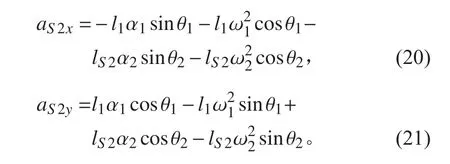
对连杆2 关于质心点求力和力矩的平衡方程,将惯性力作用于质心点上,有

式中:I2为连杆2 绕质心的转动惯量;F32x,F32y为滑块3 对连杆2 沿x 轴和y 轴的分力;F12x,F12y为曲柄1 对连杆2 沿x 轴和y 轴的分力。
对于滑块3,在x 轴方向受力,有
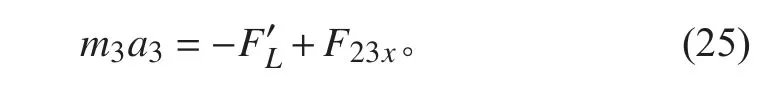
将上述关于曲柄1、连杆2 和滑块3 的5 个力平衡关系式,改写成矩阵形式,有

其中: C 为系数矩阵; F 为求解力矩阵; B为已知力和力矩矩阵,有
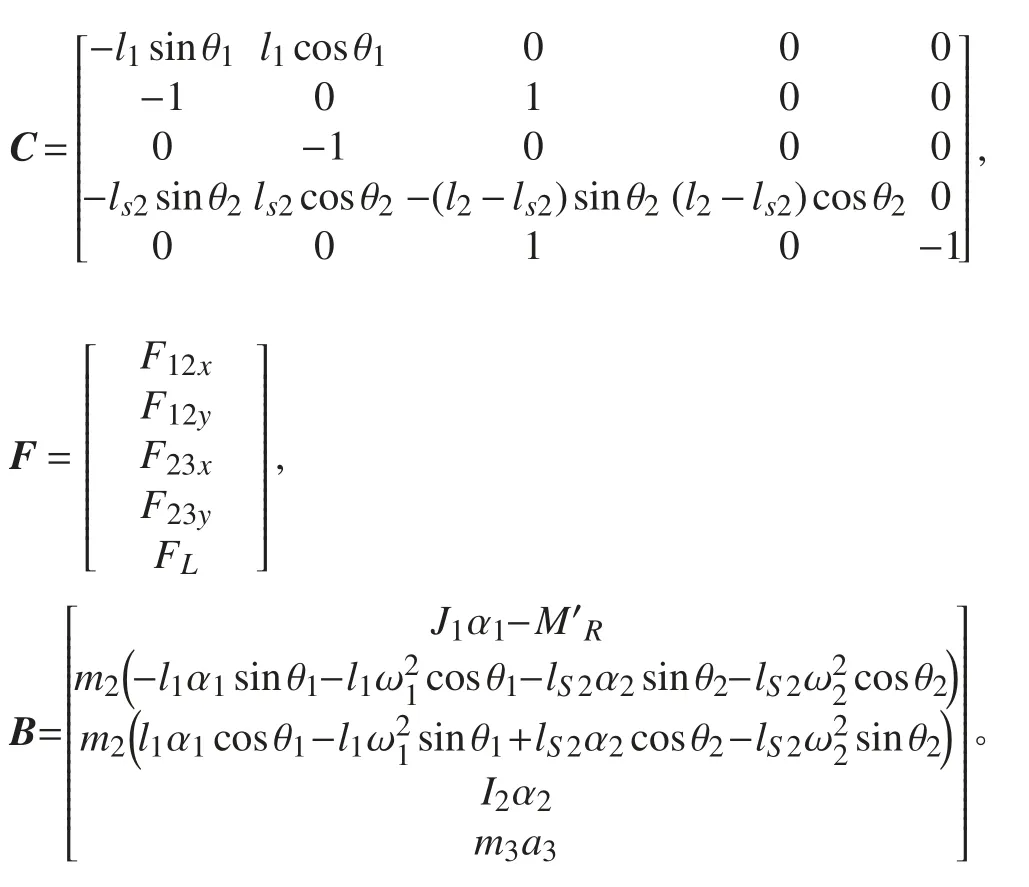
1.2.2 Simulink 仿真建模
图6 为由滑块-曲柄机构的Simulink 仿真得到的活塞杆位移与喷泵舵角映射曲线。在活塞杆向x 轴正向匀速运动中,喷泵的舵角由左满舵向右满舵变化,变化的速率略有加快,但总体上比较接近于直线。
从图7 可看出喷泵舵角从左满舵到右满舵的运动中横向误差ex会稳定在1.6×10-12m,而纵向误差ey处于-2×10-14~5×10-14m 内变动,该数值为构件长度的10-10倍,是极其微小的变化量。可见该滑块-曲柄机构的运动学分析可精确描述出各构件的运动位置。
1.3 估算喷嘴上的等效作用力
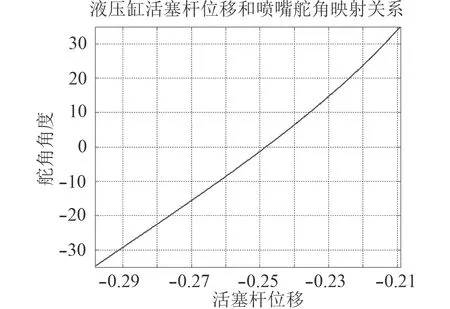
图 6 液压缸活塞杆位移与喷泵舵角映射关系Fig.6 Mapping relationship between the displacement of piston rod in hydraulic cylinder and the rudder angle of injection pump
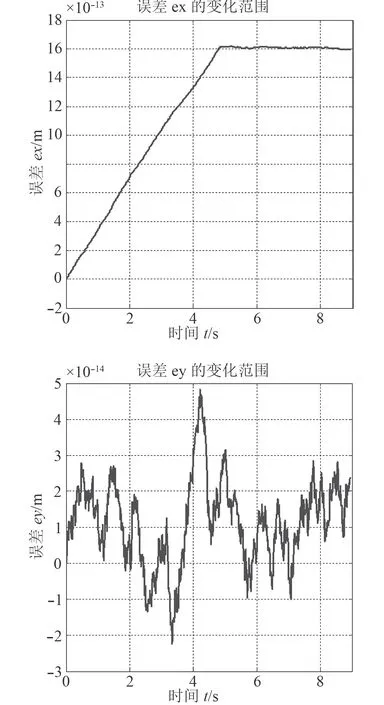
图 7 仿真计算中误差变量的变化情况Fig.7 The variation of error variables in simulation calculation
液压活塞杆的输出推力并不由自身决定而取决于外界的负载,舵机系统承受外界作用力的主导因素为喷泵水流对喷嘴的冲击作用。
1.3.1 喷嘴受力分析
如图8 所示,假定喷泵主机固定在某一转速下喷水,忽略水流沿程损失,水流经截面A、截面B 和C 截面动量方程为:
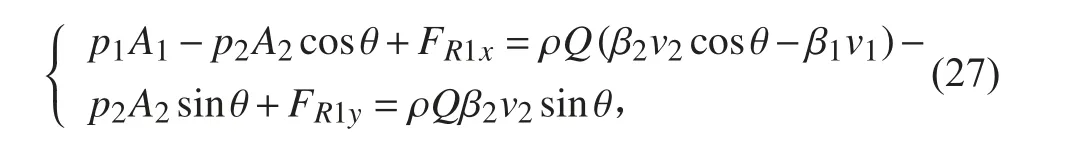
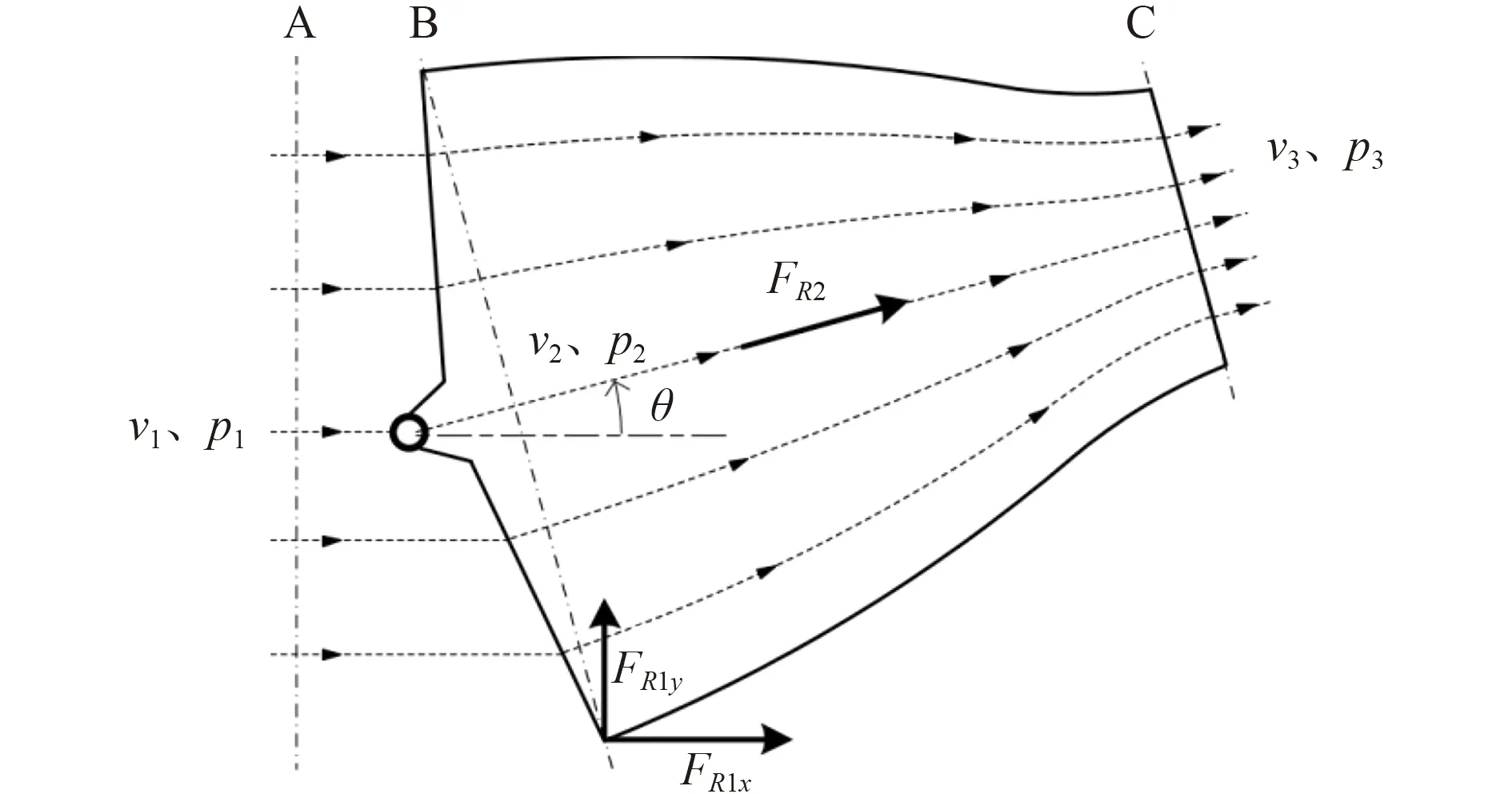
图 8 某舵角下喷嘴水流流向和受力Fig.8 The flow direction and force of injector
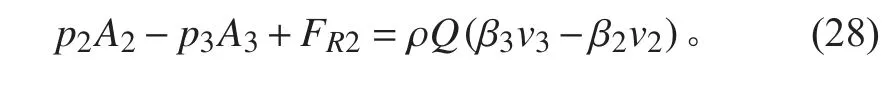
式中:p1,p3,p3,A1,A2,A3和v1,v2,v3为A、截面B、截面C 处水流的压强、面积和速度;ρ 为海水密度;Q 为喷水流量;FR1x,FR1y为水流从截面A 到截面B 喷嘴对水流沿水平和竖直方向分力,FR2为水流从截面B 到截面C 中喷嘴对水流的作用力;θ 为喷嘴角度,逆时针为正;β1,β2,β3为动量修正系数,取β1=1.03、β2=1.03、β3=1。
由参考文献[7]可知,喷泵的扬程H 与喷水流量Q 的关系为:
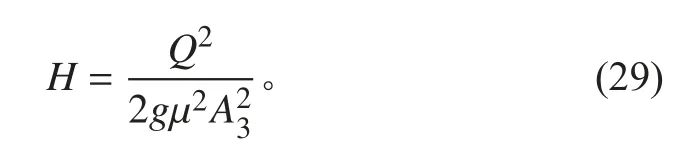
其中,μ 为喷嘴的流量系数,有
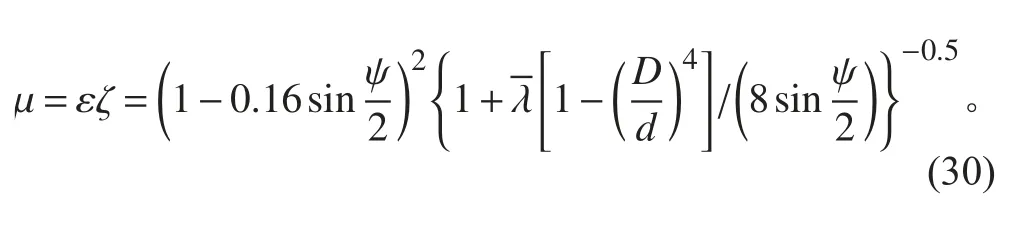
式中:ε 为喷嘴的收缩系数;ζ 为喷嘴流速系数;ψ 为喷嘴锥角;D,d 为喷嘴进、出口内径;为喷嘴的平均直径。
忽略喷嘴水头损失和水流在垂直方向的位移,假定进水为静止海水,由流体连续性方程和伯努利方程[9],可得:
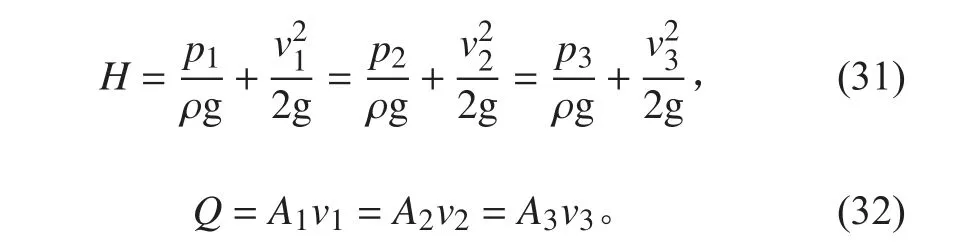
将式(29)、式(31)和式(32)代入式(27)、式(28)并简化得:
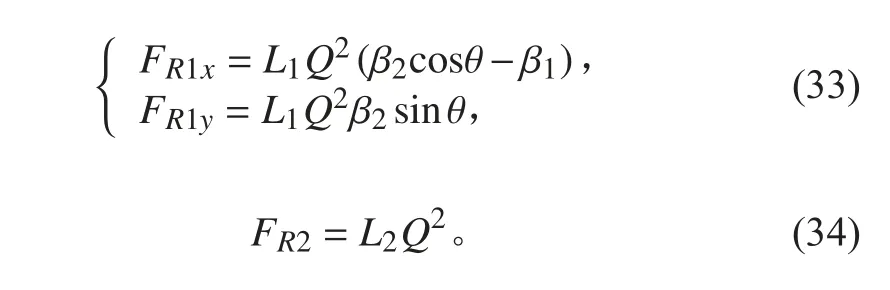
其中:
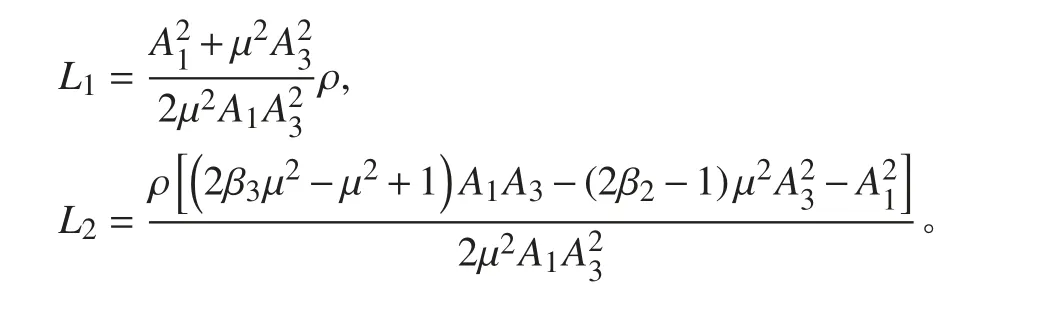
由牛顿第三定律,喷泵水流对喷嘴的反作用力为:
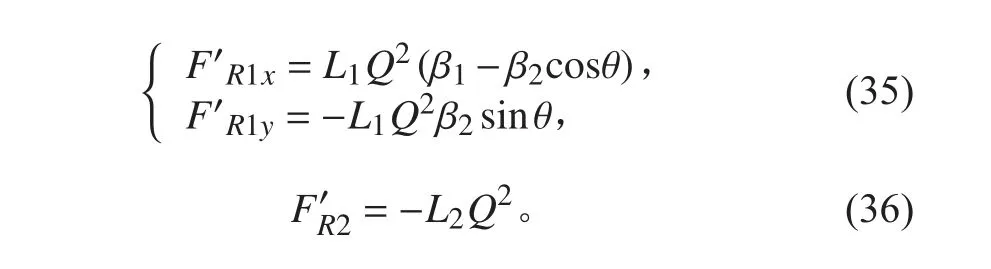
为简化分析,将水流对喷嘴的作用力等效为合力和合力矩,有
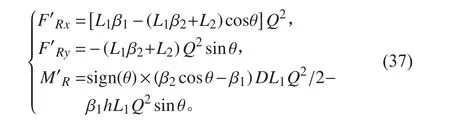
1.3.2 舵角与等效力矩关系
喷泵水流对喷嘴产生的等效作用力矩变化主要与喷泵流量Q 和喷嘴舵角值θ 有关,假定喷泵排水量固定为Q=0.25 m3/s,利用Simulink 仿真可得图9 所示的负载力矩随舵角θ 的变化曲线。在流量Q 一定时,喷嘴转向的舵角越大,负载力矩也就越大,呈非线性关系,需液压系统提供更大推力。
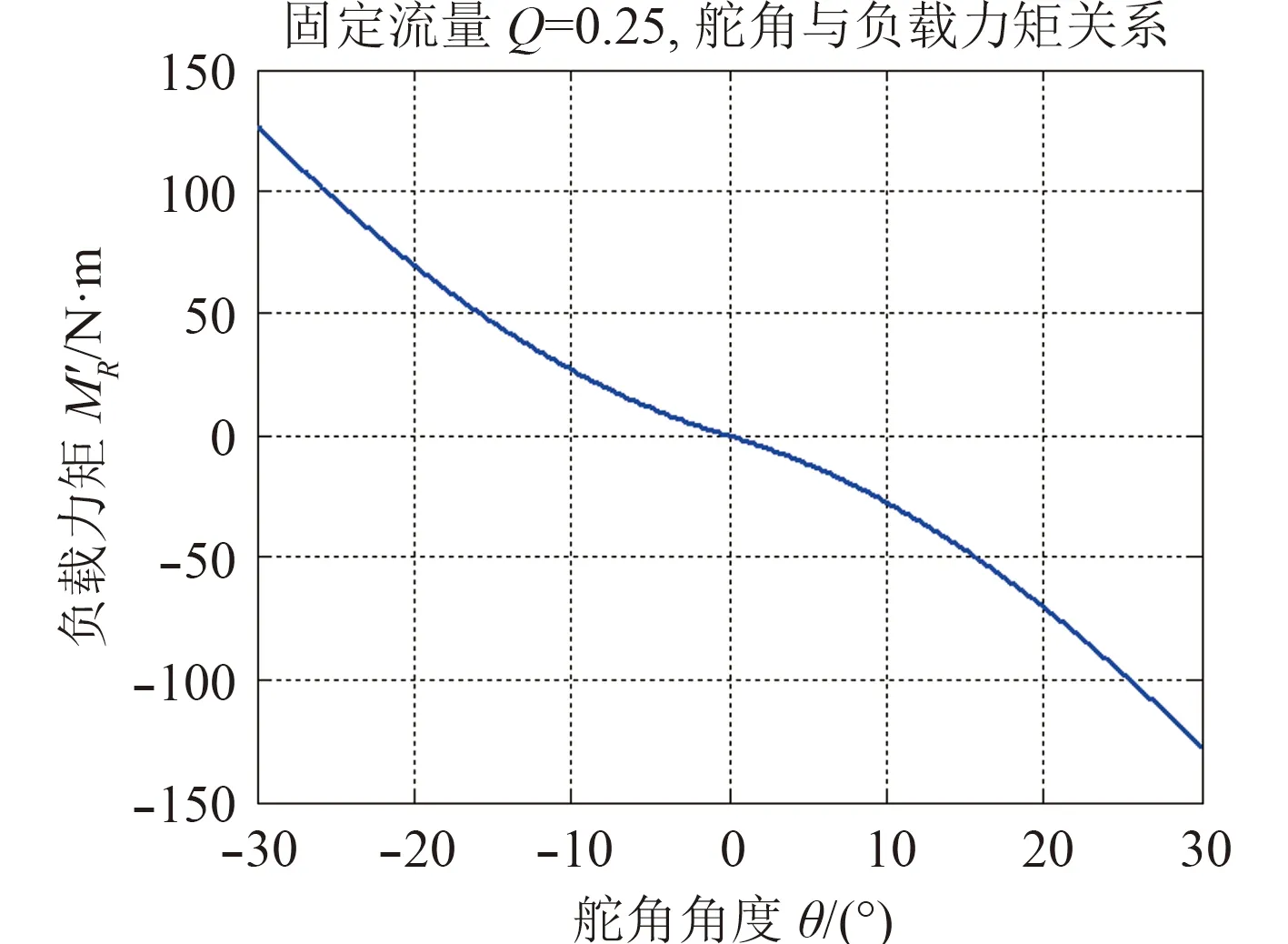
图 9 喷嘴的等效力矩随舵角的变化Fig.9 The change of equivalent moment of injector with rudder angle
2 模型整合与验证
2.1 模型整合
将伺服电机、液压系统、偏置滑块-曲柄机构以及外界水流负载整合为整体直驱式电液伺服舵机系统,如图10 所示。
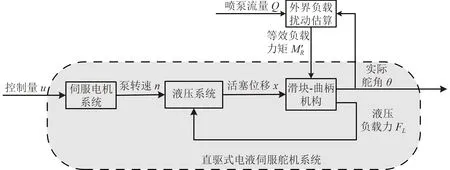
图 10 直驱式电液伺服舵机系统结构Fig.10 Structure of the direct-drive electro-hydraulic servo steering-gear system
系统输入的控制量直接作用于伺服电机系统,使得电机运动,通过减速器带动液压泵转动,随之液压泵驱动活塞杆直线运动,再经滑块-曲柄机构传递动力并将直线运动转为喷嘴转向运动,实现该舵机系统舵角操控。兼顾到该舵机系统常用工况为喷水状态,在喷泵流量为恒定时,结合当前实际舵角值可估算喷嘴的等效负载力矩,再将该负载力矩作为滑块-曲柄机构的动力学输入,计算出活塞杆的负载力并作为液压系统输入,以构建完整的舵机模型。
2.2 模型验证
根据上述思路,可搭建如图11 所示的舵机系统的Simulink 模型,其输入为电机转速以及喷泵流量,输出为实际舵角。
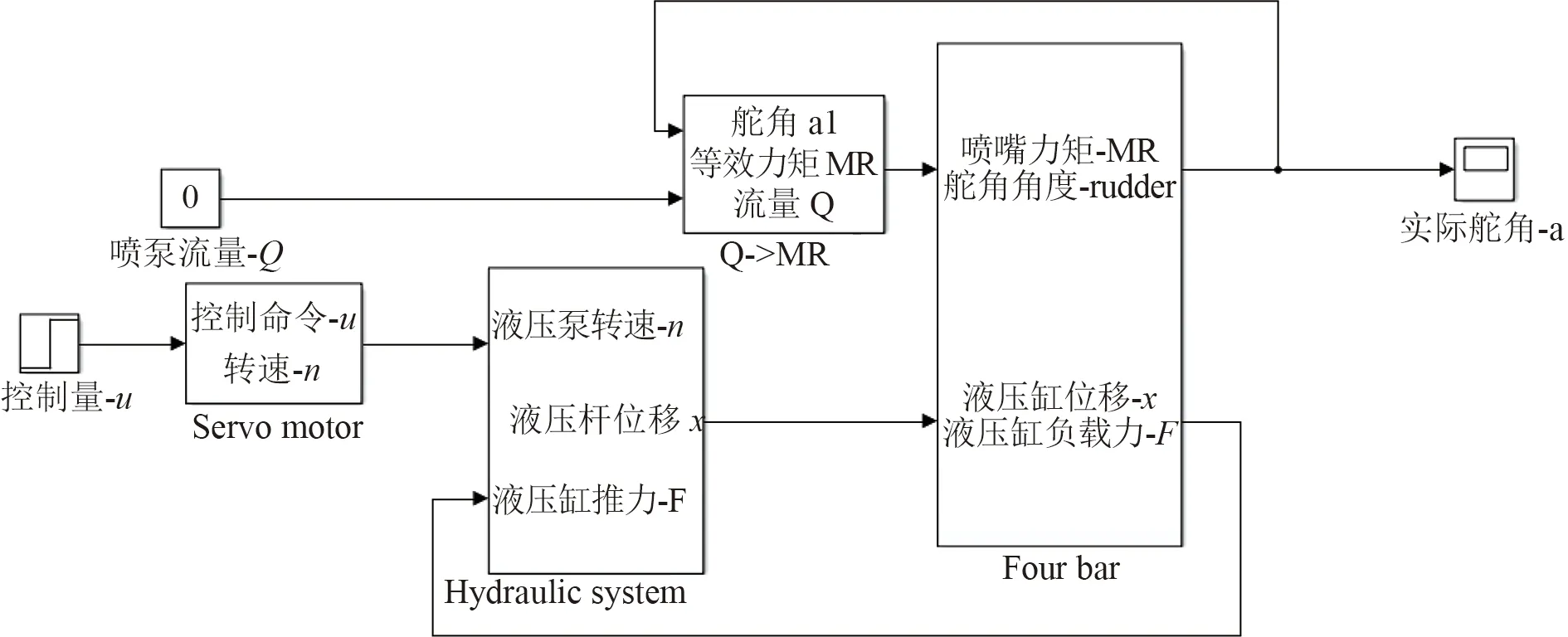
图 11 直驱式电液伺服舵机系统仿真模型Fig.11 Simulation model of direct-drive electro-hydraulic servo steering-gear system
利用伺服电机将喷泵舵角运动到最左端,再以每间隔10 000 qc 的控制值发送给伺服电机转动舵角,人工实测喷嘴转动的舵角。仿真模型中初始舵角为-35°,伺服电机的输入转速为26 r/s,即52 000 qc/s,将时间序列转化qc 值。将仿真模型0°舵角与实际系统0°舵角的采集点重合,可得如图12 所示的对比曲线。
可知,舵角实际值与仿真值的误差在±0.5°内,即仿真模型对实际系统的拟合效果较好,整体误差值较小,验证了该模型一定的有效性。
上述模型验证是在喷嘴无水流负载下进行的,而无人艇处于喷水状态下,整个喷嘴都位于水面下并且承受着高速水流冲击,是人工无法测量该舵角值,并且喷泵流量无法给出,故暂不考虑加载负载后模型的有效性。
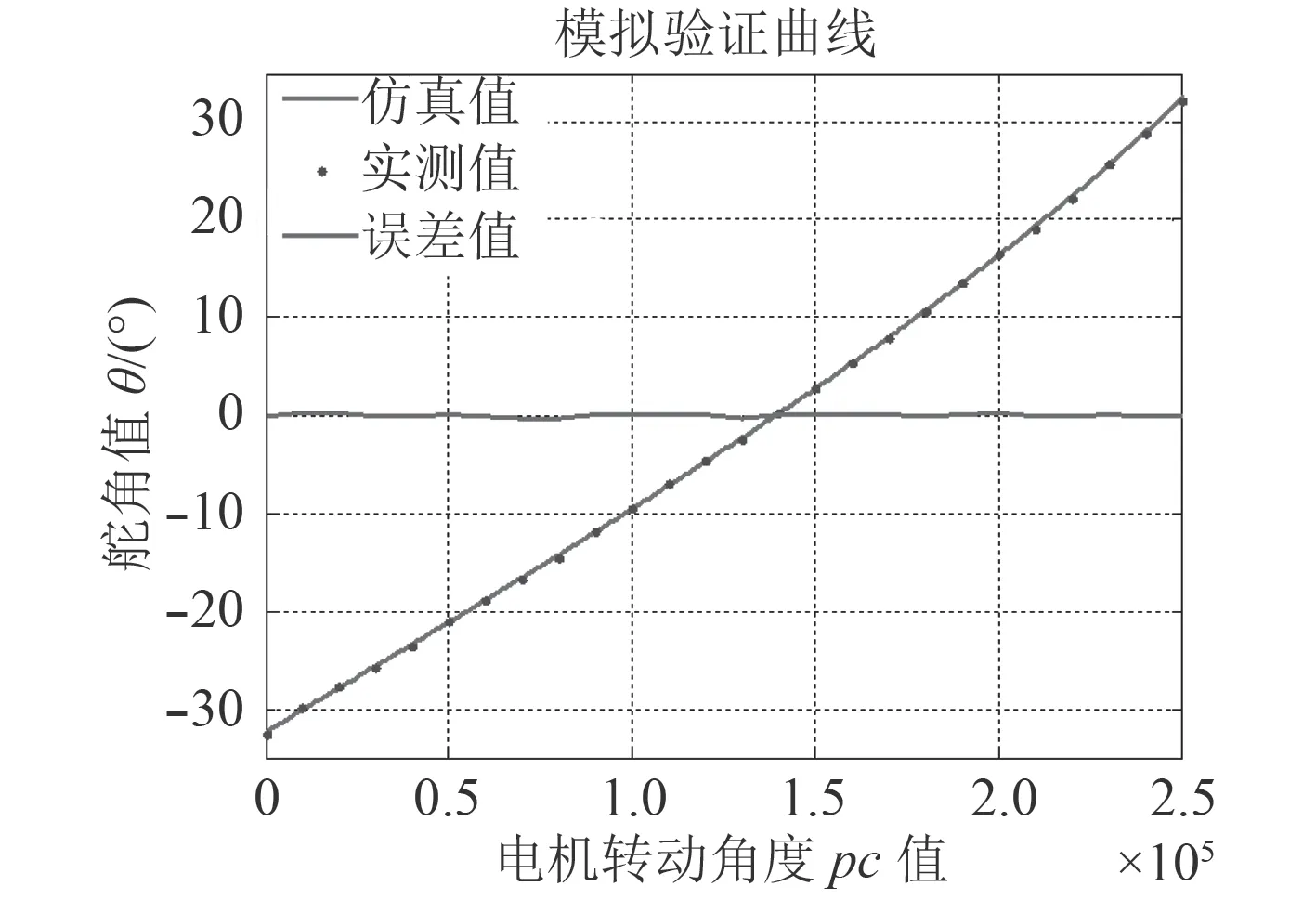
图 12 仿真系统与实物系统对比曲线Fig.12 Comparison curve between simulation system and real system
3 结 语
本文介绍喷水推进无人艇直驱式电液伺服舵机系统组成,分别对伺服电机、液压系统、执行机构、外界喷水负载建立了仿真模型,并整合舵机模型,验证其有效性。
在液压系统添加了执行机构等效的滑块-曲柄模型,以此分析活塞杆位移和舵角运动关系,并基于动力学计算了变化的活塞杆负载力。考虑喷泵水流对喷嘴的冲击,估算喷嘴在不同喷水量和舵角情况下的等效负载力矩,并作为滑块-曲柄机构的输入。

