基于机器学习的船舶阻力预报模型研究

张乔宇，黄国富，金建海

(1.中国船舶科学研究中心，江苏 无锡 214082；2.中船重工（上海）节能技术发展有限公司，上海 210000)

0 引 言

船舶阻力预报是准确预报船舶快速性的重要内容之一，目前常用的预报方法有模型试验，CFD 数值模拟和一些近似估算方法。在现代船舶工程中，近似模型方法很好地解决了船舶CFD 计算的复杂耗时问题[2]，避免了模型试验的繁琐过程与较高成本。陈爱国等[3-4]基于系列60 船舶试验数据，建立了最佳的BP 神经网络系统,拓展了系列60 的应用范围。李纳等[5]建立了基于广义回归神经网络的“船型要素—船体阻力”数学模型，并结合遗传算法完成了船型要素的优化设计，优化结果可以为玻璃钢渔船初步设计提供技术参考。肖振业等[6]采用支持向量和神经网络方法建立了国际船模KCS 总阻力的近似模型，表明了支持向量机近似模型具有较好的预测精度和可推广能力。Devrim[7]在低雷诺数条件下，采用神经网络方法对双体船中心片体的形状、布置位置进行了选择优化。通过与模型试验结果的分析对比，表明了这种外形设计的有效性，可以减少波干扰所引起的阻力。Jong-hyun Lee等[8]基于遗传规划的非线性数学函数的方法，在船型设计初期对船舶附加阻力进行预报，通过预测结果与试验结果、理论结果的对比分析，表明该方法满足精度要求，具有一定的适用性。

采用近似模型方法解决船舶阻力相关问题已经受到许多学者的广泛关注，但近似模型方法有很多，为了提高船舶阻力预报的准确性，应该有针对性地选择预报模型。为此，本文以公开的泰洛系列船模试验数据为例，研究目前机器学习模型在船舶阻力预报中的应用效果。泰洛系列船模试验是以一艘军舰为母型进行系列改型[9]，生成不同宽度吃水比B/T、棱形系数Cp、排水体积长度系数1 000 ∇/L3的船模，在不同傅汝德数Fr 下进行系列阻力试验，最终得到剩余阻力系数试验数据。现取B/T，Cp，1 000 ∇/L3，Fr 作为模型构建输入向量，剩余阻力系数作为输出向量。为检验模型泛化能力且避免原始数据集分布对模型训练的影响，随机选取数据集的80%作为训练集、20%作为测试集，进行20 组不同排列组合试验，以测试样本预报值和真实值的均方误差和相关系数作为衡量模型适用性的评价指标，并通过4 组不同B/T 插值样本进一步检验，以选出较好的预报模型。

1 机器学习模型原理

本文选取机器学习模型中6 种经典的回归预报模型进行试验论证，即KNN 近邻回归、多元线性回归、岭回归、标准支持向量回归、3 层BP 神经网络、回归树。

1.1 KNN 近邻回归

KNN 近邻回归属于非参数回归方法，是通过搜索历史样本库中与新样本相似的样本数据来进行预测，需要考虑的主要因素包括：从历史样本库中选取与新样本距离较近的样本个数（K 值）、近似程度度量方式、K 个历史样本的权重函数和内部实现算法。本文选取比较常用的欧式距离度量方式，公式如下：

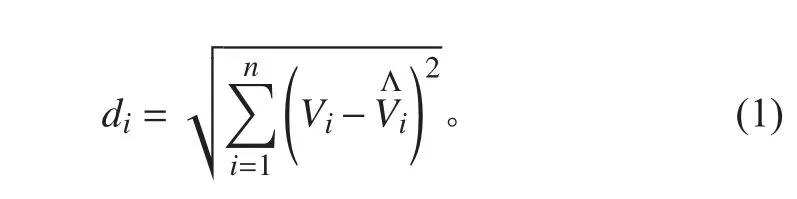
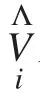
1.2 多元线性回归与岭回归

多元线性回归是自变量多于一维时的回归形式，具体的方程形式为：

式中： xi为 输入数据向量； w为各输入数据向量对应的权值矩阵； yi为真实输出值。

多元线性回归的目标是寻找使真实值与预测值误差平方和最小的一组权值矩阵。误差平方和可写为：

上式对 w求导后，令其导数为0 进而取极小值点，解出 w如下：

由于上式需要对矩阵求逆，当矩阵非满秩时求逆会出现问题，因此采用缩减系数法来解决这一问题，岭回归即是其中的一种。岭回归是在矩阵 xTx上加一个λI （I 是m×m 的单位矩阵）使矩阵非奇异， λ的取值需要根据具体问题进行训练，使误差最小化。该方法不仅可以解决矩阵 xTx无法求逆的问题，也可在估计中引入偏差，并且λ 限 制了 w之和，从而减少了不重要的参数[12]。

1.3 支持向量回归

支持向量回归是通过特征空间中估计内积的核隐式，实现输入变量到高维特征空间的映射，然后在高维特征空间中构建线性回归函数，对应原空间非线性问题的求解[2]。数学表达式为：

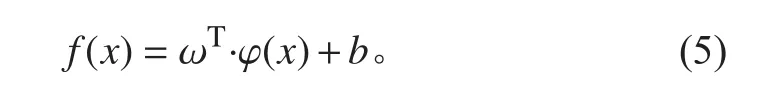
式中： f(x) 为回归系数， ω 和 b分别为回归函数的法向量和偏移量； φ(x)表示特征映射函数。支持向量回归算法可以描述为以下问题：

式中： C表示惩罚系数； ξi，为松弛变量； ε表示拟合精度[13]。通过引入拉格朗日乘子与核函数的方法求解该问题，最终可将式（6）化为：

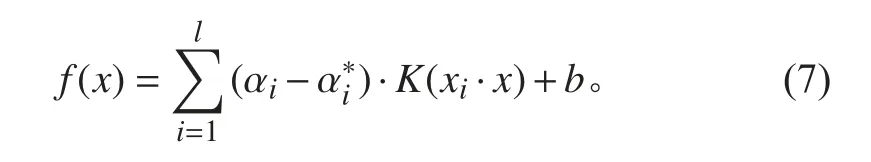
因此，支持向量回归模型的设计需要选择合适的精度参数 ε，惩罚系数C 以及核函数。

1.4 3 层BP 神经网络

人工神经网络基本单元如图1 所示。图中x1～xn为输入值， yi为输出值， wij表示从神经元 j到神经元i的连接权值，θ表示阈值， φ为激活函数，单个神经元的运算过程如下式：

本研究的目标分析物是合成麝香，对水样的预处理主要包括过滤、萃取和浓缩。采用玻璃纤维滤纸在真空条件下进行水样过滤，使溶解相和颗粒相分离。对于溶解相，量取1.5 L过滤后的水样至分液漏斗中，加入 10 µL 500 ng·mL-1 DnBP-d4 回收率指示物标准溶液，混匀后再加入50 mL二氯甲烷进行液液萃取（3次）；对于颗粒相，将玻璃纤维滤纸中的颗粒相样品加入到索氏抽提器中以150 mL二氯甲烷静置萃取24 h。将萃取液过无水硫酸钠以去除剩余水分，收集萃取液于250 mL蒸发瓶中，旋转蒸发浓缩至1 mL左右，最后氮吹浓缩至约 150 µL。

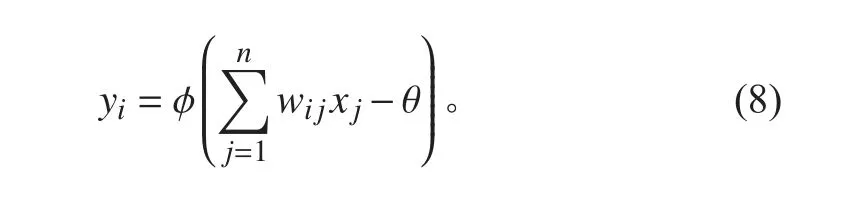
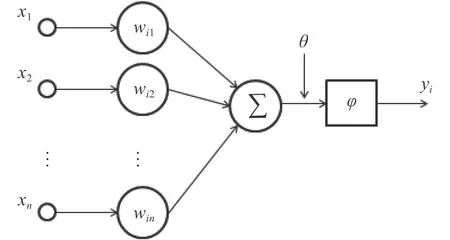
图 1 人工神经网络基本单元Fig.1 Basic unit of artificial neural network

BP 神经网络的主要思想为对于样本若干个输入向量以及与其对应的目标向量，根据网络实际输出与目标向量之间的误差，选用合适算法修改权值和阈值，使网络输出层的误差平方和达到最小[14]。

1.5 回归树

回归树是一种非参数监督学习方法，基本思想是通过给定数据集的特性采用某种算法推断出简单的决策规则，进而预测目标变量的值。树构建算法中常用的是CART 算法，即使用二元切分来处理连续性变量。具体算法过程如下：

在训练数据集所在的输入空间中，递归地将每个区域划分为2 个子区域并决定每个子区域上的输出值，构建二叉决策树[15]。

1） 选择最佳切分变量j 与切分点s，求解

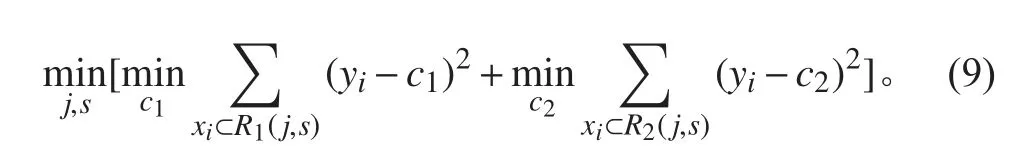
式中： c1， c2为 R1， R2两个划分区域的代表值，以使区间实际值 y1， y2与代表值之间的平方差达到最小。

2） 遍历变量j，对固定的切分变量j 寻找切分点s，找到可使式（9）达到最小值的（j,s），用选定的（j,s）划分区域并决定相应的输出值：

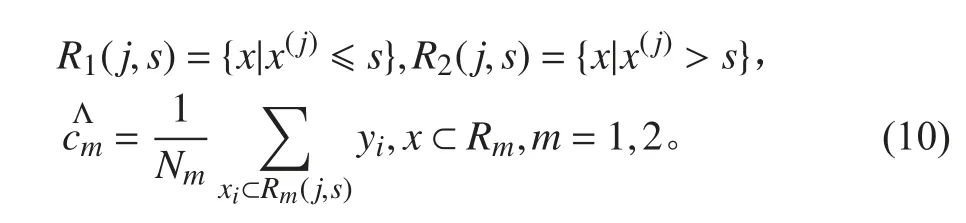
3） 继续对2 个子区域重复步骤1 和步骤2，直至满足条件，

4）最终可将输入空间划分为若干区域，假定M 个：R1，R2，···Rm，并生成回归树：

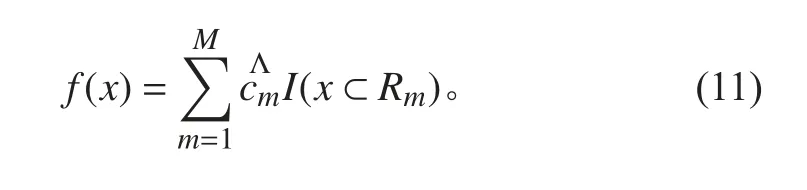
2 机器学习回归模型设计

2.1 KNN 近邻回归模型设计

为选取合适的k 值、权重函数和内部实现算法，开展不同组合参数的方案设计，得到均方误差与相关系数随k 值数的变化曲线，如图2 所示。

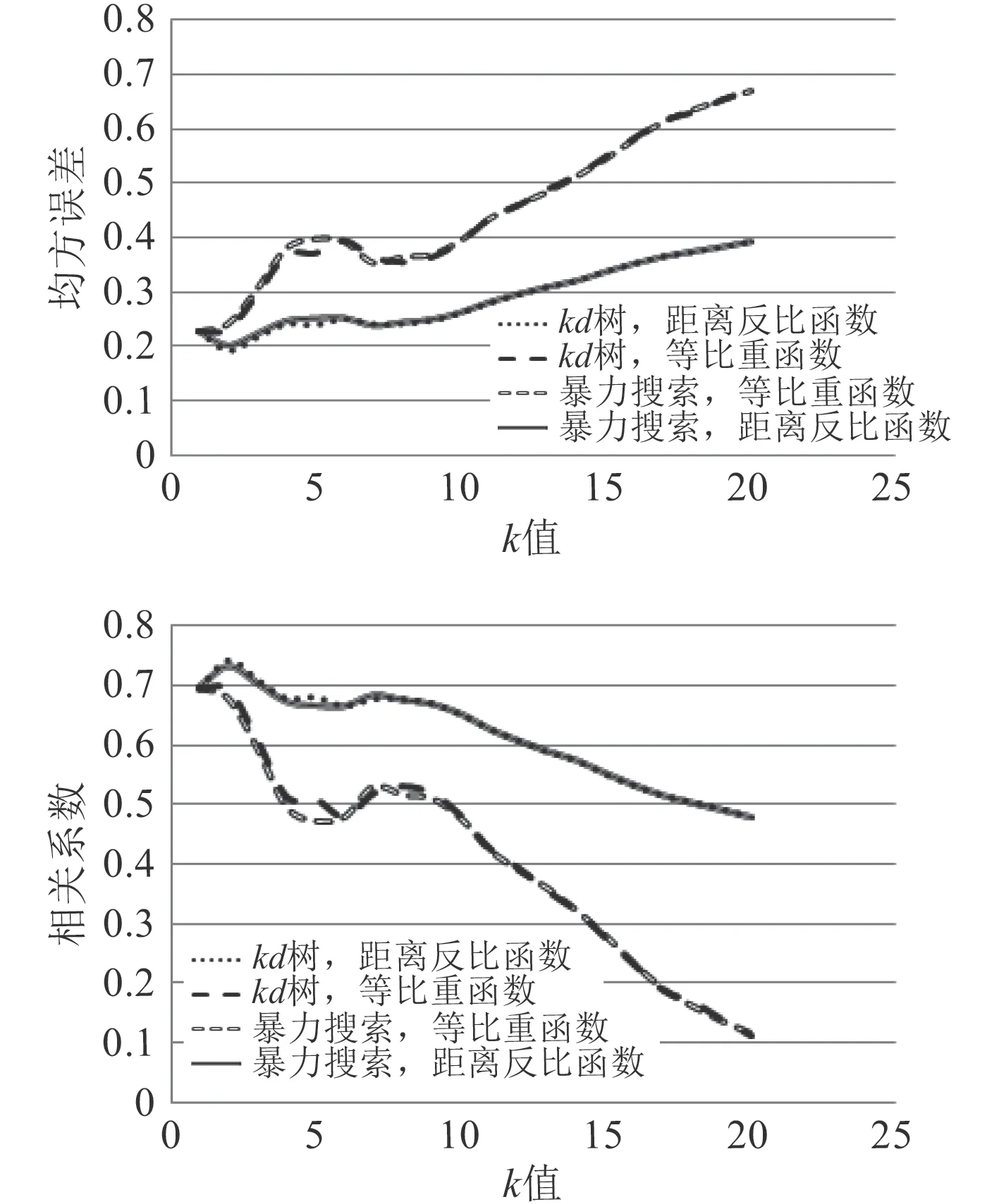
图 2 均方误差、相关系数随不同KNN 算法参数变化曲线Fig.2 Variation curves of mean square error and correlation coefficient with different KNN algorithm parameters

由图2 可知，当k 值为2 时，相关系数出现峰值，而后随k 值的增加逐渐减小，均方误差也在k 值为2 时出现低谷，之后随k 值增加而增大；而在内部实现算法与权重函数的选择上，kd 树算法与距离反比函数的组合最优。故本文选择k=2,kd 树算法，距离反比函数的KNN 近邻回归模型。

2.2 岭回归模型设计

岭回归主要调节参数为 λ值，岭回归模型中对 λ在0.1～1.0 之间进行参数寻优，均方误差与相关系数变化曲线如图3 所示。可以看出，最佳的 λ值只能看出在0.1 附近，因此继续对 λ在0.01～0.1 之间寻优，结果如图4 所示。当 λ=0.1 时，预测效果最好。

2.3 支持向量回归模型设计

根据文献[13]可知，在预报船舶阻力时，支持向量回归模型需要考虑的参数有惩罚系数 C、核函数与拟合精度 ε，现对3 个参数进行组合方案设计。现对4 种常用核函数进行试验，结果如表1 所示。均方误差与相关系数随惩罚系数 C 、拟合精度 ε的变化曲线如图5 和图6 所示。因此，本文选取多项式核函数、惩罚系数 C 为0.16、拟合精度 ε为5 的支持向量回归模型。

2.4 3 层BP 神经网络模型设计

通过参考文献[3]，选择贝叶斯正则化函数作为训练函数，均方误差规则化函数为性能函数，隐层传递函数为双曲正切S 形函数，输出层传递函数为线性函数。而隐层神经元数则参考经验公式（其中，m 为输出节点数，n 为输入节点数， a可取1～10 之间的整数）选取调优范围，具体变化情况由图7 所示。从可以看出隐层神经元数为18 时最优。

图 3 均方误差、相关系数随岭回归 λ值变化曲线（0.1～1.0）Fig.3 Variation curves of mean square error and correlation coefficient with λ number of ridge regression (0.1～1.0)

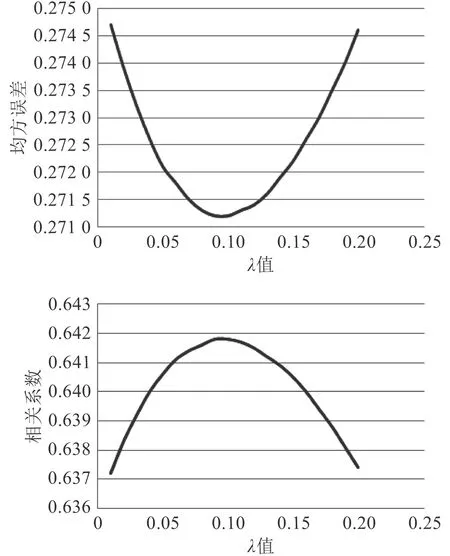
图 4 均方误差、相关系数随岭回归 λ值变化曲线（0.01～0.1）Fig.4 Variation curves of mean square error and correlation coefficient with λ number of ridge regression (0.01～0.1)

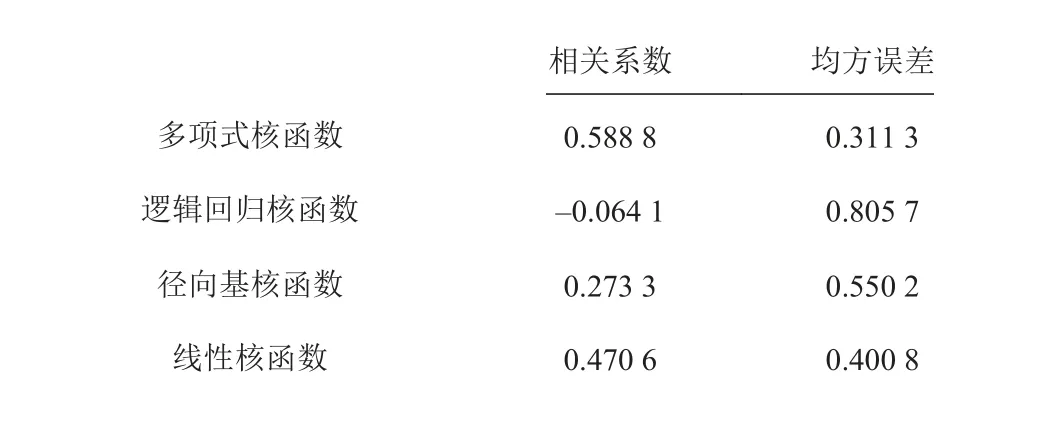
表 1 不同核函数的相关系数与均方误差比较结果Tab.1 Comparison results of correlation coefficients and mean square error of different kernel functions

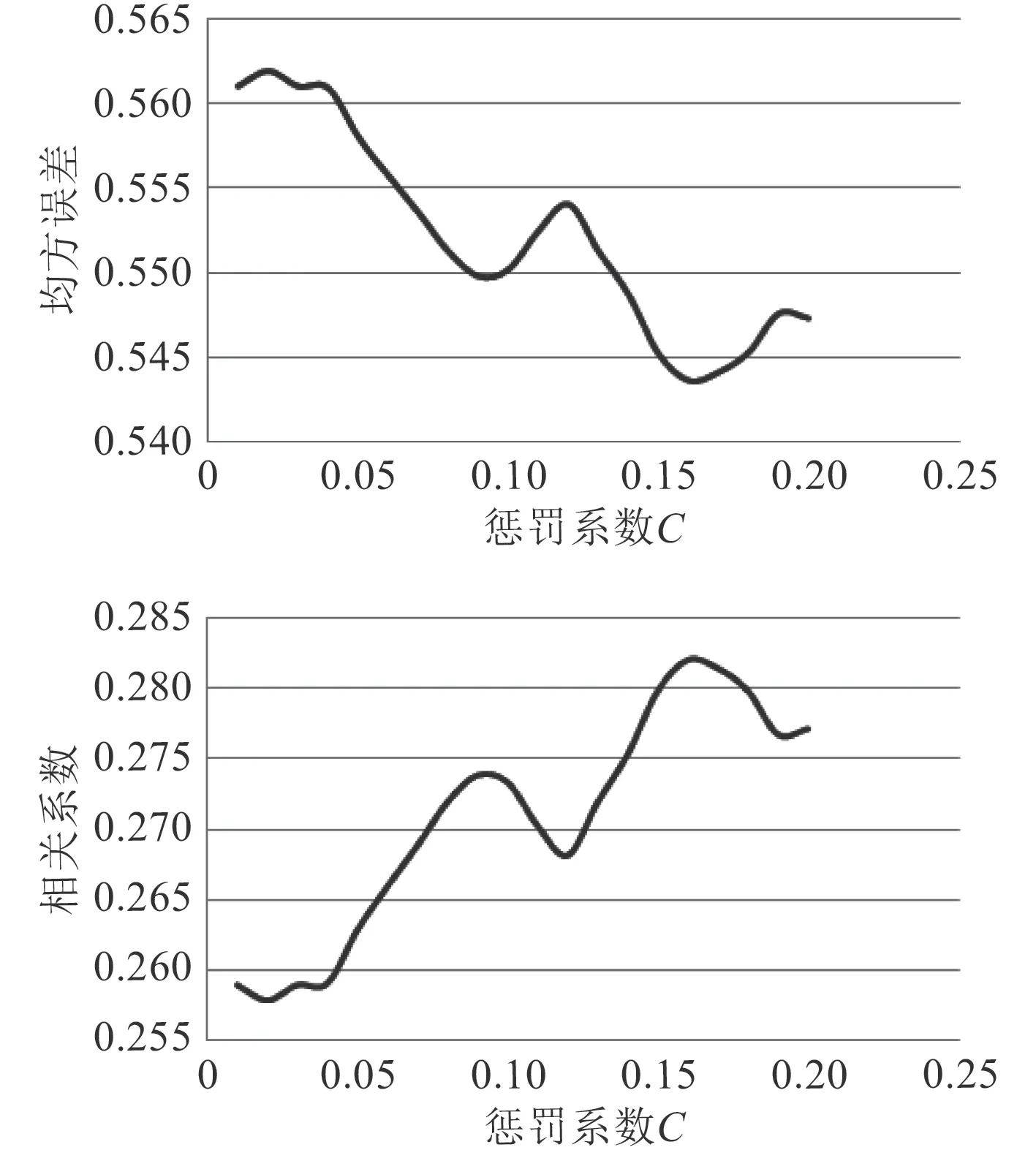
图 5 均方误差、相关系数随惩罚系数 C变化曲线Fig.5 Variation curves of mean square error and correlation coefficient with penalty Coefficient C

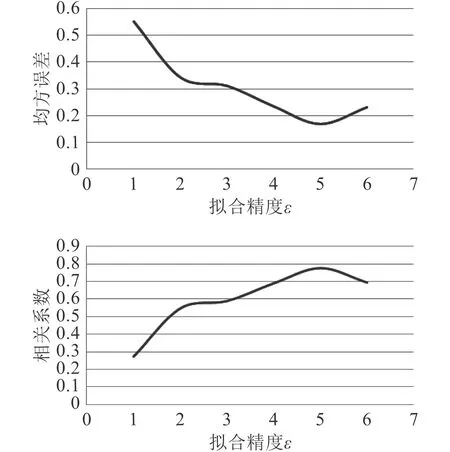
图 6 均方误差、相关系数随拟合精度 ε变化曲线Fig.6 Variation curves of mean square error and correlation coefficient with fitting precisionε

图 7 均方误差、相关系数随隐层神经元节点数变化曲线Fig.7 Variation curves of mean square error and correlation coefficient with number of nodes of hidden layer neurons

3 船舶阻力预报模型比较

采用以上6 种机器学习回归模型进行阻力预报试验，得到20 组不同数据集样本排列方式的相关系数与均方误差平均值，如表2 所示。由于训练和测试样本都是采用的原始数据，为了验证各模型的泛化能力，选择各模型20 组中拟合效果最好的一组，对相同的Cp，1 000 ∇/L3与Fr，进行B/T 为2.5，2.75，3.25，3.5 的4 组剩余阻力系数值进行预报，同时采用直线内插法[16]对4 组剩余阻力系数值进行计算。预报剩余阻力系数值与内插法所得值的均方误差与相关系数如表3所示。由此可见，回归树模型在6 种机器学习模型中预报效果最好。

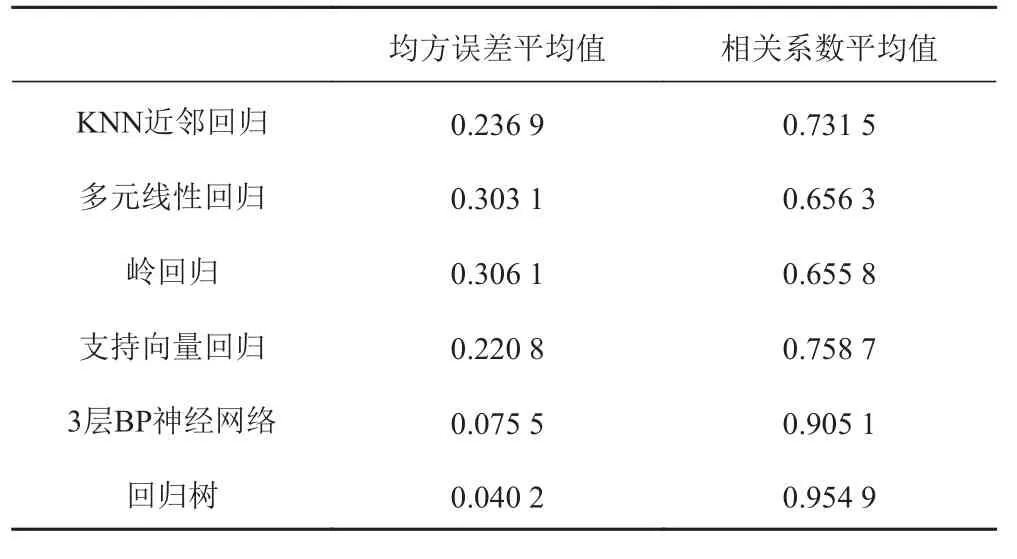
表 2 机器学习模型剩余阻力系数预报结果对比Tab.2 Comparison results of residual resistance coefficient prediction of machine learning model

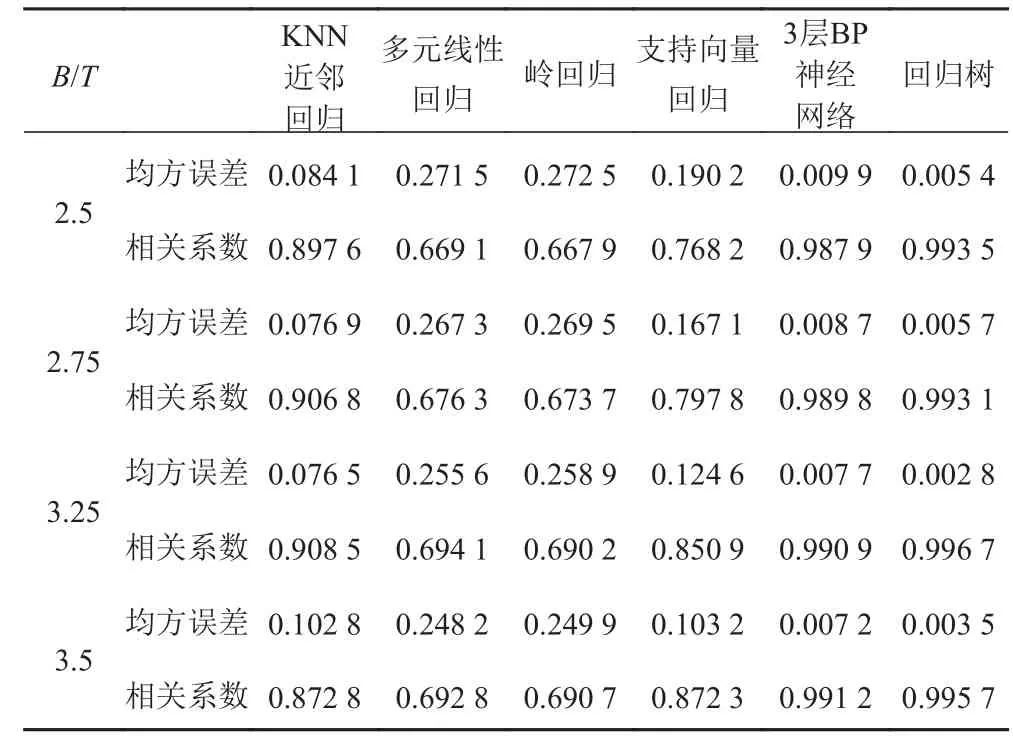
表 3 四组插值样本剩余阻力系数预报结果对比Tab.3 Comparison results of residual resistance coefficient prediction of four sets of interpolated samples

4 结 语

利用泰洛标准系列船模原始试验数据，采用6 种经典机器学习回归模型，对船舶剩余阻力系数进行预报，通过每种模型预报效果对比，得到以下结论：

1）通过训练机器学习回归模型，在泰勒标准系列船模试验数据的参数范围内，可以较精确地对船舶剩余阻力系数进行预报，避免了人工查谱的的繁琐过程，且预报效率较CFD 数值模拟方法要高。

2）对于机器学习近似预报模型可以进一步调整算法，以提高对船舶阻力的预报精度。

3）针对不同的船舶阻力系列数据，根据数据集的特点与分布规律，选择合适的近似模型并进行调优，从而设计出具有较高泛化能力的船舶阻力预报模型的方法切实可行。