基于最优空时自适应处理的箔条云干扰抑制方法

李 冉, 栗 苹, 贾瑞丽

(北京理工大学 机电学院,北京100081)

0 引言

空时自适应处理最初只是针对机载多通道动目标显示(MTI)雷达,目前已被诸多需要进行自适应传感器时域和空域处理的领域所采用[1-2],且从地面环境和水下环境等其他应用环境中都得到了很好的发展[3-4]。空时处理的目的就是在杂波或干扰占据的角度——多普勒处放置一个抑制凹口,该凹口将取决于感兴趣的目标角度——多普勒信息[5]。

箔条是一种常用的无源干扰手段。目前针对箔条云干扰的抑制方法可以分为以下几类[6-8]:

a)基于箔条极化特征的抗干扰方法,文献[6]定义了共极化比和垂直共交极化比,提出了以共极化比和垂直共交极化比为联合鉴别量的抗箔条干扰方法;

b)基于箔条频率特性的抗干扰方法文献[7]:建立了箔条锥动的回波信号模型,综合考虑了箔条丝锥动对雷达回波信号频谱的影响,现有文献已经对箔条云回波特性有了多角度广泛研究,但一般都只考虑了箔条云中单根箔条造成的影响并只进行简单的矢量加和,缺乏对箔条云整体响应的分析;

c)基于箔条统计特性的抗干扰方法,文献[8]选取了六个参数,并利用模糊函数构造箔条云统计特性来分辨箔条云,这六个参数分别为反射率、差分反射率、互相关因子、线性化的差分相位、反射率标准差和差分相位标准差。

针对箔条云整体空时域特性的研究尚很欠缺,本文基于箔条云的统计模型,研究了箔条云的空时域特性,且利用空时自适应处理理论推导了抑制箔条云回波的最优空时处理方法。

1 箔条云的空时域特性

箔条云完全散开的条件下,箔条云后向散射回波电压服从瑞利分布,相位服从均匀分布[7]。基于空时自适应处理(STAP)的前提为无源干扰波是均匀的,且满足不相关复反射率因子的广义平稳过程。而箔条云回波不仅取决于发射天线方向图,也与箔条云回波固有特性有关。定义ηj为

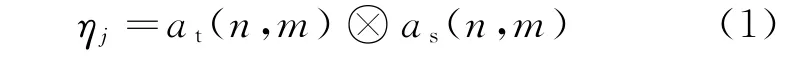
式中:ηj为考虑了箔条云回波电压幅度和相位的复随机向量;{at(n,m)}服从瑞利分布;{as(n,m)}服从均匀分布;n为理想的天线单元个数;m表示m个脉冲重复间隔(PRI)时间延迟。

箔条云模型的数学期望为

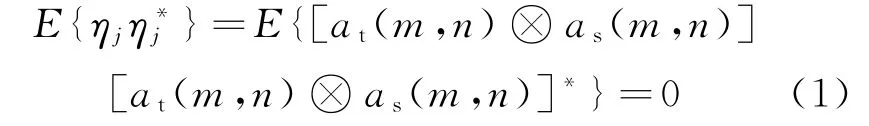
箔条云回波满足不相关复反射率因子的广义平稳过程模型。

根据空时自适应原理,为了方便分析只考虑一个N阵元构成的均匀线性阵列,相干处理间隔内由固定脉冲重复间隔的M个脉冲组成。对于一个理想角度—多普勒矢量S,那么一个确定波束形成器的权矢量w可以由线性方程组w's=1,w'j1=0…w'jNM=0得到。当箔条云存在时,可采用统计信号处理的手段来解决确定性零馅的局限性问题。特别地,箔条云干扰可视为随机过程,则通过统计最优化过程可得到最优空时波束。首先利用STAP原理分析箔条云的空时域特性。STAP系统应用多接收通道的电子扫描天线,这组阵列天线通过测量各通道线性相位差对回波进行空域采样,不同相位参数对应不同信号到达方向。

选取第1通道为参考通道,则第n通道的特定到达方向的相位可表示为

式中:τn为回波在参考通道和第n通道间的时延;ω为角频率,ω=2πf,f为传播信号频率。

如图1所示,根据天线与箔条云的几何关系可得

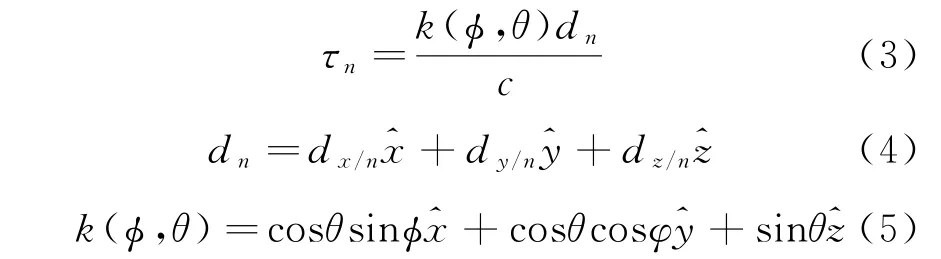
式中:dn为箔条云相对于第n通道相位中心坐标系的位置矢量{dx/n,dy/n,dz/n};{^x,^y,^z}为第n通道相位中心坐标系的单位矢量;k(φ,θ)为单位矢量,方向垂直于箔条云回波;φ为方位角;θ为俯仰角;c是波速。

将(3、4、5)代入(6)可得

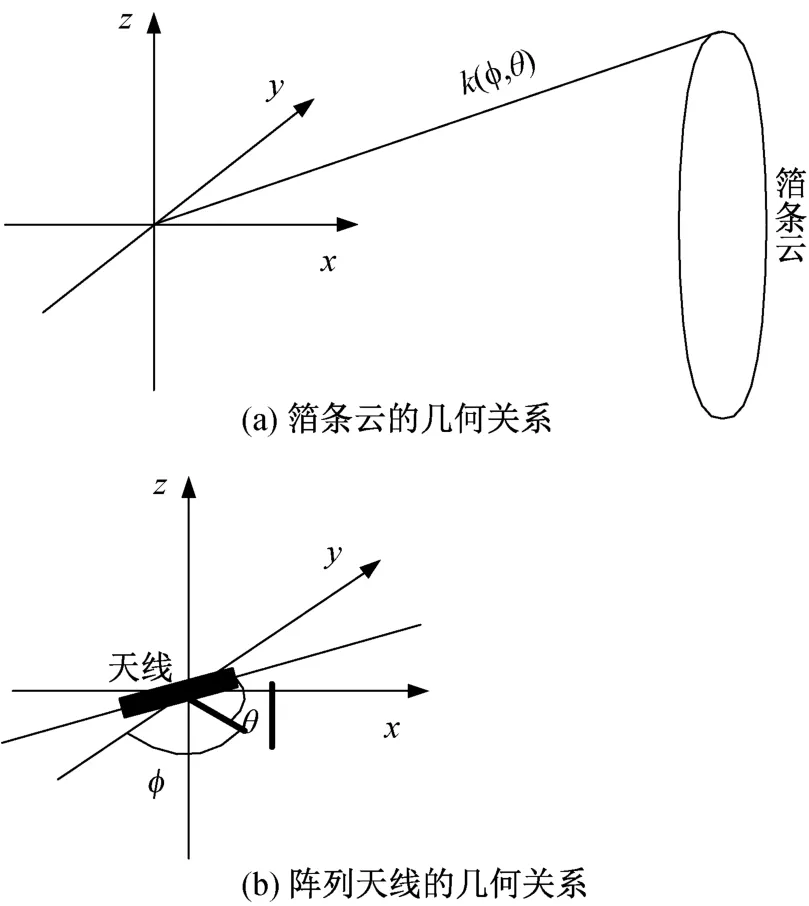
图1 箔条云与阵列天线的几何关系

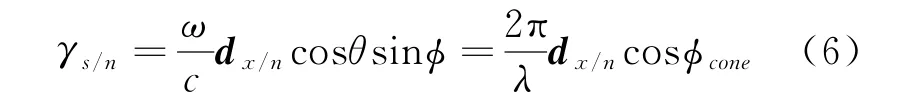
式中:cosφcone第n通道相位中心坐标系x轴与单位矢量k(φ,θ)的夹角。

可得空域信号矢量为xs=asss(fs),as为一个随机数即箔条云相位系数,集合{as}服从均匀分布,fs为空域频率fs=(dx/m/λ)cosφcone;且空域导向量ss(fs)为

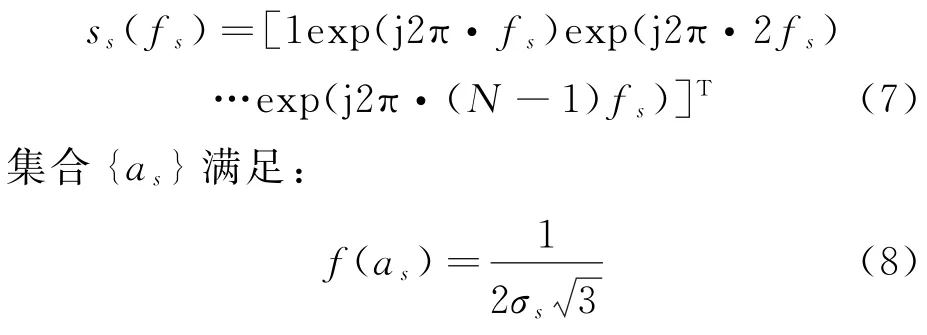
式中:f(as)为as的概率密度;为相位变化方差。

另一面,分析计算箔条云的时域特性。假设传播信号是一个长度为M的周期脉冲序列,且重复周期为T。定义r0为箔条散射点到天线相位参考通道的距离。由于箔条与雷达的相对运动,导致脉间的距离变化为Δr。因此可得时间延迟τm为

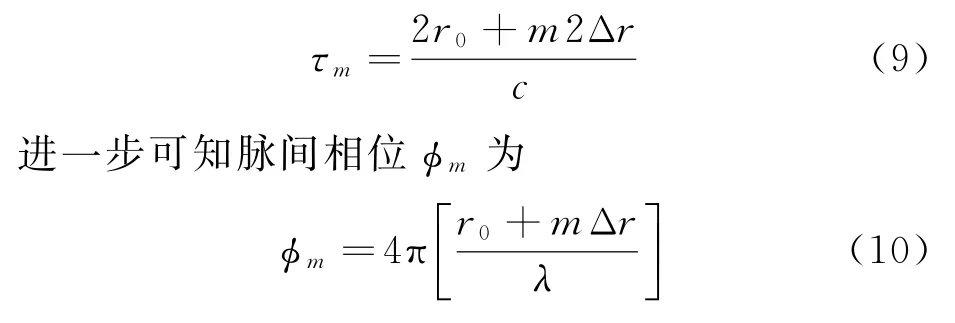
则多普勒频率fD为

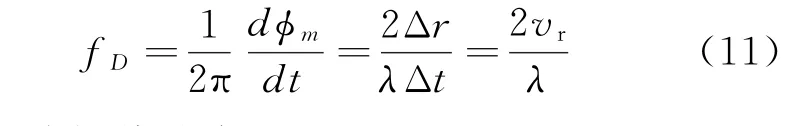
式中:vr为视线速度。

时域信号矢量xt=atst(~fD)为,~fD为归一化多普勒频率~fD=fDT,at是一个随机数即箔条云回波电压包络系数,{at}集合服从瑞利分布,时域导向矢量st(~fD)为

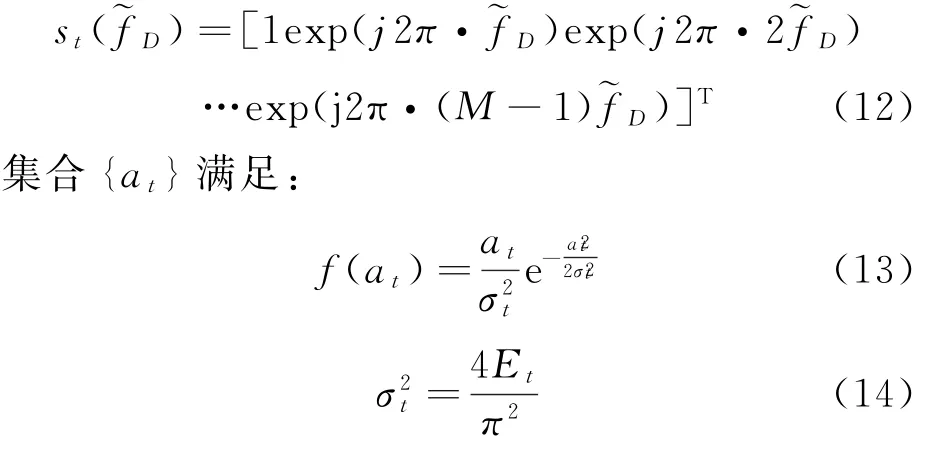
式中:f(at)为at的概率密度为箔条云回波幅值方差;Et为箔条云回波电压幅度均值。

对比式(7)和式(12),箔条回波在空域和时域的响应具有相似的数学表达式。则可得空时信号导向矢量ss-t(fs,~fD)为,⊗表示Kronecker积:

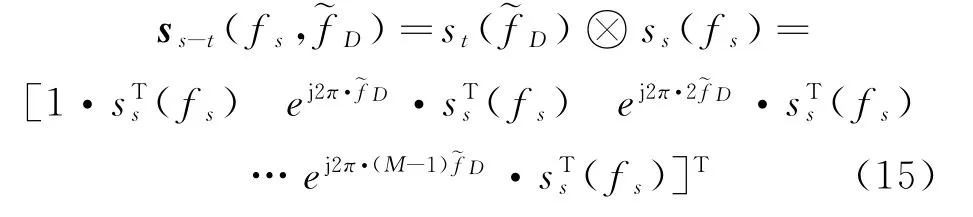
图2给出了箔条云空时特性的仿真结果。其中设置N=16,M=14,总自由度为224;干扰噪声比(JNR)为30 dB,噪声水平为0 dB;箔条云相位系数{as}服从均匀分布,电压幅值系数{at}服从瑞利分布,并且方差=1。图2(a)为箔条云协方差矩阵特征值分布,(b)为基于傅里叶变换的箔条云功率谱估计。由图2可知,箔条云回波功率谱在空时域呈陡峭的锥型,且在不同角度—多普勒方向上回波功率变化剧烈。

2 最优空时处理抑制干扰技术

利用最优空时处理原理,推导最优空时波速形成器,可以有效抑制箔条云干扰。如图3所示的空时线性波束形成器,其由N个理想的天线单元——空域自由度和M个脉冲重复间隔(PRI)时间延迟——时域自由度组成。为了最大化信号干扰噪声比(SINR),需要选择最优的空时权系数ω[5]。

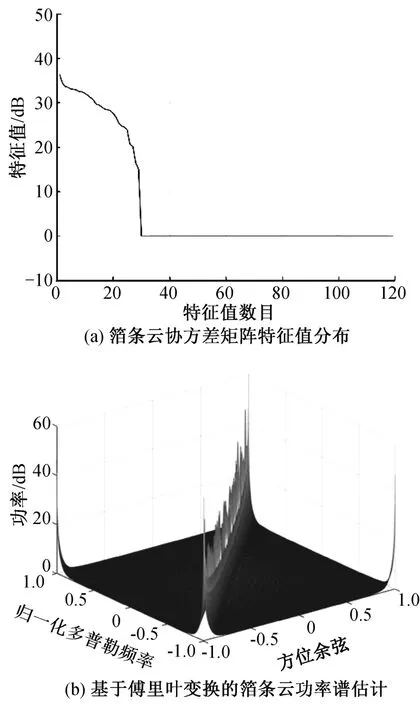
图2 箔条云空时特性

权系数ω可表示为

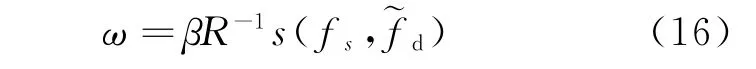
式中:R∈CCNM×NM为NM×NM维干扰和目标的协方差矩阵;β为常数标量并不影响SINR输出(可由SINR的定义推导此结论,此处不赘述);s(fs,~fd)∈CCNM为NM维期望信号的空时导向矢量,可表示为

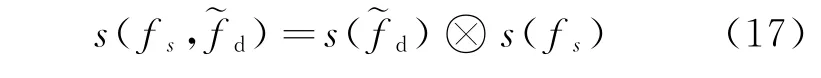
式中:s(~fd)为时域导向矢量;s(fs)为空域导向量。

由于干扰响应平方的期望可表示为

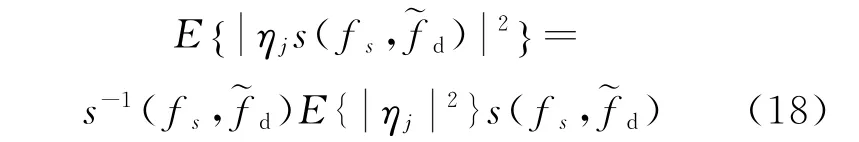
因此,可得最优波束成型器的高分辨谱估计为

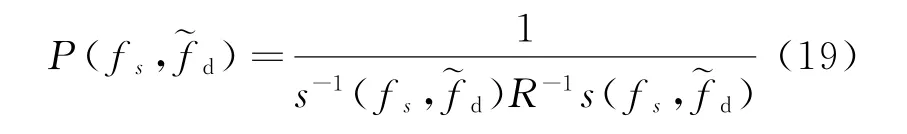
进一步联合加权处理可以表示为

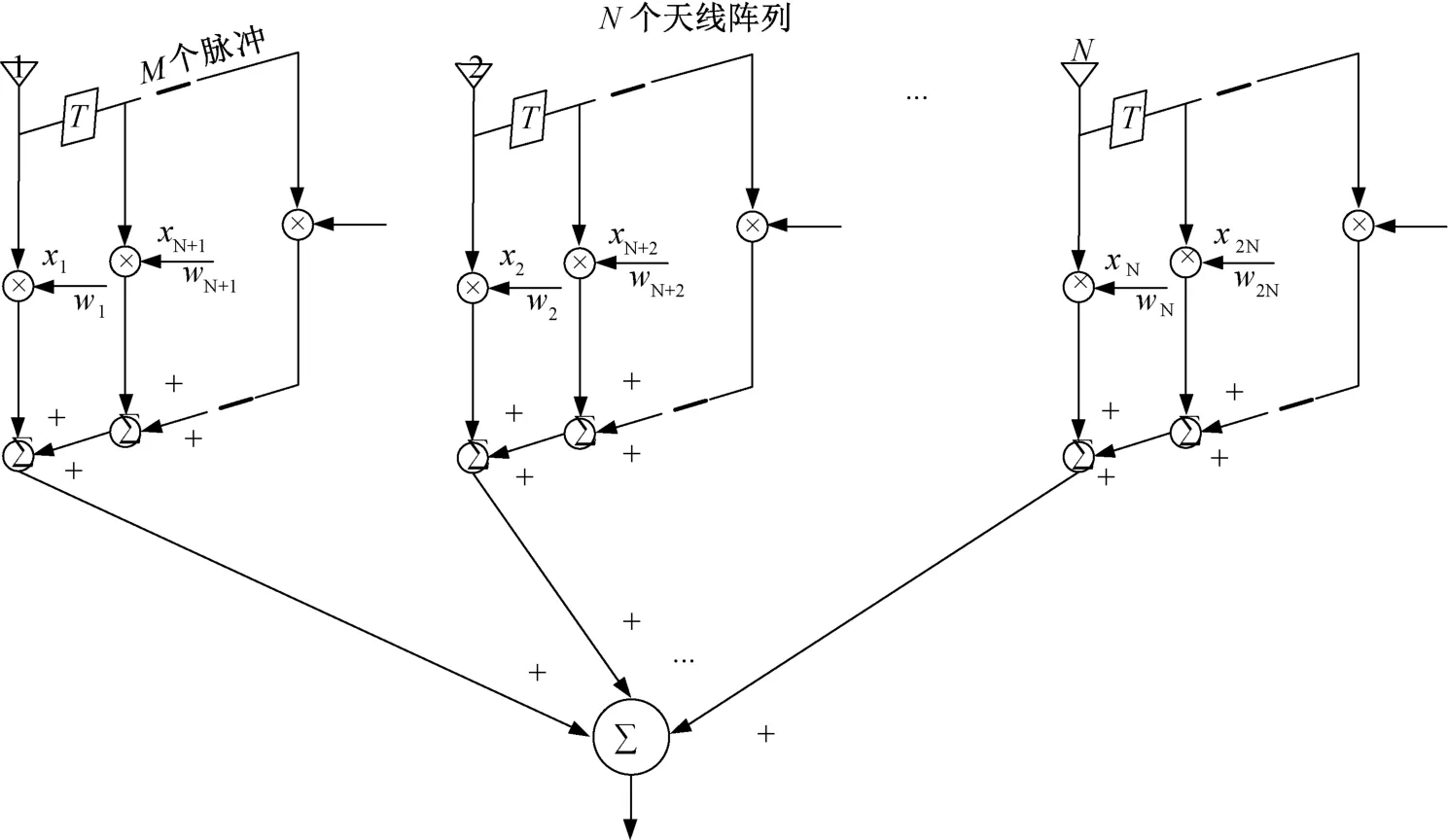
图3 空时波束形成器

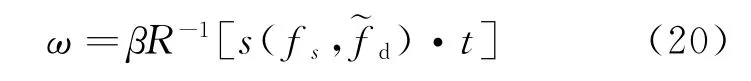
式中:t=td⊗ts;t∈RRNM为期望NM维加权;ts∈RRN为N维角度加权;td∈RRM为M维多普勒加权。

3 仿真实验

为了验证本文方法的有效性,下面通过仿真实验方法进行分析,并考察箔条云空时特性修正模型对干扰抑制方法性能的影响。由于实际的干扰环境通常不是先验已知的,因此利用有限样本估计的手段去近似得到式(16)中要求的干扰协方差矩阵。在本例中,为保证输出SINR为最优处理的3 dB左右,至少选取448个理想箔条云回波样本,且样本中没有任何目标信号。然后,采用傅里叶变换对理想箔条云回波样本进行功率谱估计,将其代入波束成型器的高分辨谱估计式(19),计算得到期望NM维加权t。结果如图4最优空时波束方向图所示,箔条云干扰与目标回波存在角度和多普勒频率加权,其中参数设置为N=16,M=14,JNR为60 d B,β=1。

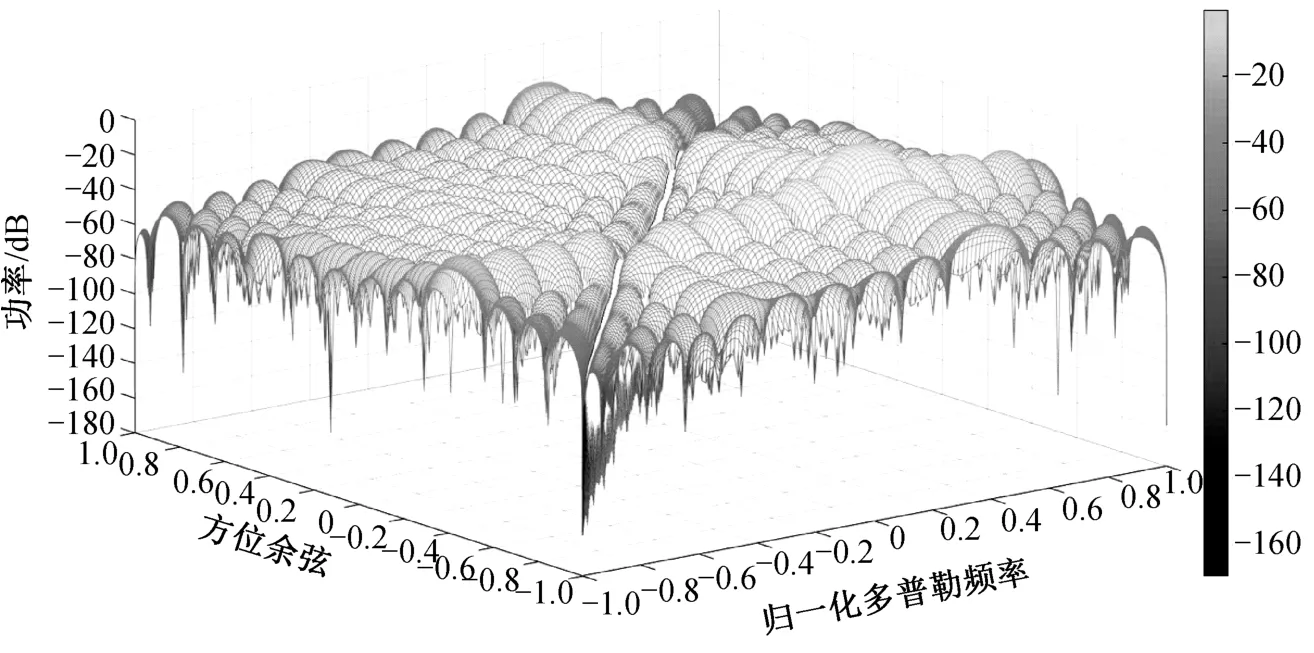
图4 最优空时波束方向图

4 结论

为提高雷达抗箔条云干扰能力,分析了箔条云的空时特性,得到了基于最优空时处理的箔条云干扰抑制方法。结果表明文中提出的干扰抑制方法,可成功对箔条干扰信号进行抑制,从而有效提高雷达对抗箔条云干扰的性能。