基于改进PSO-BP神经网络算法在一般盗窃犯罪预测中的应用
朱小波 次晋芳
(上海公安学院治安系 上海 200137)
0 引 言
在大数据时代下,犯罪预测是维护社会稳定的重要基础,对于打击犯罪和有效开展预防犯罪工作具有深远意义。广州大学教授柳林认为,探索如何有效地开展犯罪防控不仅是公安部门的工作重点,更是理论界研究的热点和难点[1]。目前有关犯罪预测的研究主要分为两大部分。一是基于日常活动理论[2],将犯罪条件归结于嫌疑人、合适的侵害目标、防范力量的缺失三部分相互作用的结果。日常活动理论指出犯罪活动与物理环境间具有复杂的相关关系[3],可根据犯罪活动相关影响因子,实现对于犯罪风险区的预测[4-5]。二是基于GIS空间分析统计与时空建模,利用犯罪时空数据,分析犯罪活动分布的时空规律,挖掘影响犯罪的相关因子,建立模型实现犯罪热点的预测[6-7]。
随着社会的快速发展,盗窃犯罪作案模式也越来越多,其影响因子也变得复杂多样,线性的预测分析模型已不能满足目前财产犯罪的需要。神经网络模型通过机器学习、数据训练能描述更多复杂的非线性相关关系[8]。在国内,柳林等[1]通过运用随机森林和时空核密度方法对不同周期犯罪热点预测效果进行对比,发现了两类预测方法的不同适应性。中国人民公安大学孙菲菲等[9]提出了一套可应用于微观犯罪预测的改进的随机森林算法,并且通过模拟实验证明了该算法对海量犯罪数据的良好分类和预测结果。在国外,文献[10]运用两种不同的分类算法,即朴素贝叶斯算法和决策树算法,对美国不同州的“犯罪种类分布”进行预测,实验结果表明,决策树算法的准确率相对更高。文献[11]通过城市指标和随机森林回归来预测犯罪并量化城市指标对凶杀案的影响,该方法在位于巴西的研究区域内可以达到97%的准确率。文献[12]运用风险地形建模(Risk Terrain Modeling,RTM)与其他犯罪预测技术相比较,发现RTM在日本福冈的车辆盗窃案件方面的预测效率大约是其他技术的两倍。上述这些基于数理统计的算法研究能在一定程度上对犯罪进行预测,但是鉴于某一算法自身的局限性,有必要采用改进的算法或是融合算法来提高预测的准确性。
PSO-BP在许多领域的预测研究都得到了广泛的应用,但在犯罪研究领域的实践尚不多见。本文旨在分析一般盗窃案件的影响因子,并通过模型对比实验得出适用于该类犯罪预测的优化算法,为警方提供量化的分析和预测结果,同时也为我国大城市的盗窃犯罪治理提供一定的借鉴。
1 研究区域概况
芝加哥市是美国仅次于纽约、洛杉矶的第三大都会区,其位于伊利诺伊州,东临五大湖,都市区内人口约290万,与周边郊区共同组成的大芝加哥地区人口超过900万。芝加哥“罪案之都”的称号难免让人不寒而栗。根据芝加哥市警察局网站数据显示,2015年-2017年该局共接报362 673起报警,其中财产犯罪占240 334起。该局一般将30多种犯罪类型归纳成为三大类:(1) 暴力犯罪,包括攻击、抢劫、殴斗、性侵犯、谋杀等;(2) 财产犯罪,包括纵火、一般盗窃、入室盗窃、汽车盗窃等;(3) 破坏生活质量犯罪,包括破坏财物、吸食毒品、卖淫等。在财产犯罪的细分类型中,一般盗窃犯罪报警量为182 673起,占整个财产犯罪的76%,总犯罪量的50.36%。可见,一般盗窃犯罪在该市之猖獗。与美国其他的大城市如纽约、波士顿、华盛顿、洛杉矶相比,芝加哥市的该类犯罪接报数量也同样是最高的。
2 数据预处理
2.1 犯罪数据集介绍
本文使用的数据集来源于芝加哥市警察局的公民执法分析和报告系统。该数据集包括了2015年1月1日至2017年12月31日芝加哥市警察局接报的所有犯罪事件的案由、地址(经纬度)、时间、案情描述等22个字段。本文抽取字段名为“Theft”即一般盗窃的数据,总量为182 673条。
运用ArcGIS(地理信息系统)软件对所有一般盗窃犯罪点在芝加哥市的799个人口统计区(Census Tract)级别的地图上进行显示,随后使用该软件的Join功能,计算得出每个人口统计区2015年-2017年的一般盗窃数量,即Crime count。
2.2 一般盗窃犯罪数量异常点检测
箱线图是利用数据的五个统计量:最小值(Min)、下四分位数(Q1)、中位数(Median)、上四分位数(Q3)与最大值(Max)来检验数值分布的一种方法。Crime count的箱线图如图1所示。因异常值偏离较边缘值较远,为清晰显示箱线位置,将纵坐标上限设500。
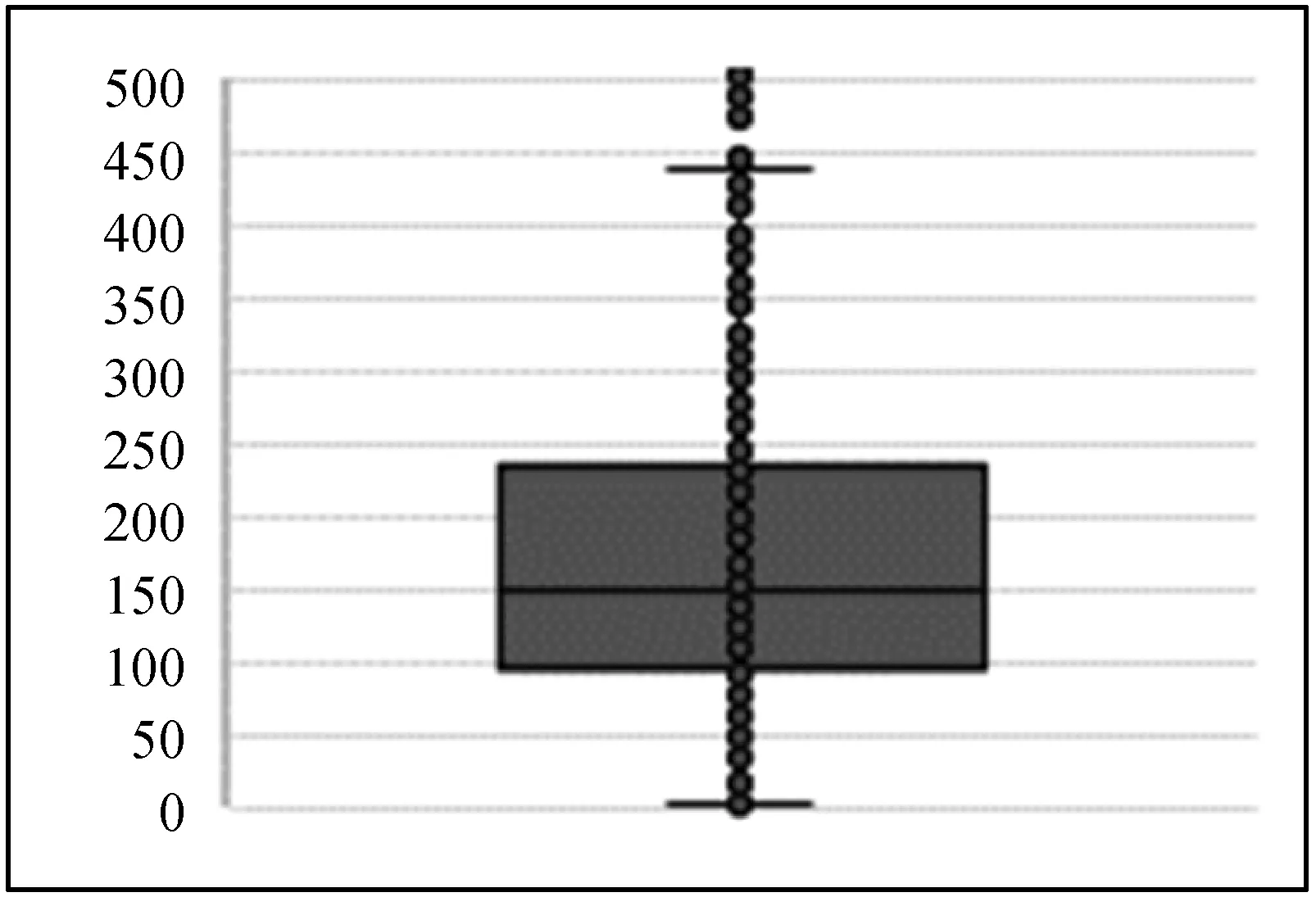
图1 Crimecount的箱线图
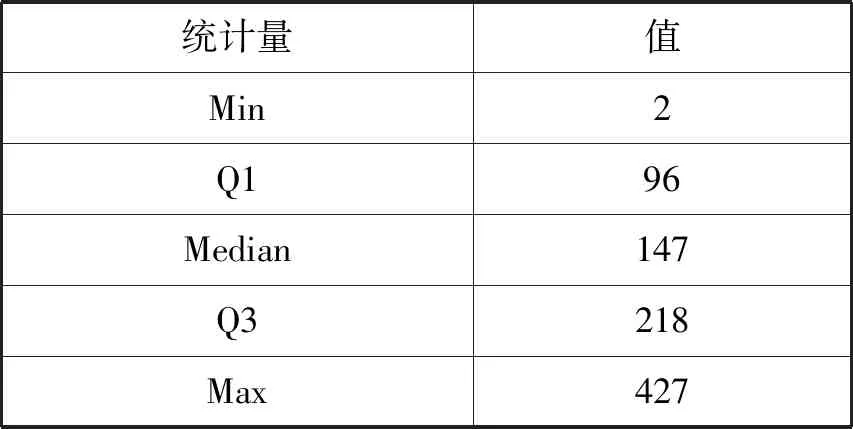
箱线图中存在一个矩形,上限为Q3,下限为Q1,矩形内部存在一条横线即是中位线,对应于中位数。矩形上下边缘的外侧存在两条横向的线段,这两条线段的端点为异常值的截断点,对应的数值分别为Q3+1.5IQR和Q1-1.5IQR。从箱线图可以看出Crime count存在异常点。Crime count的详细描述性统计量信息如表1所示。

表1 Crimecount的描述性统计量
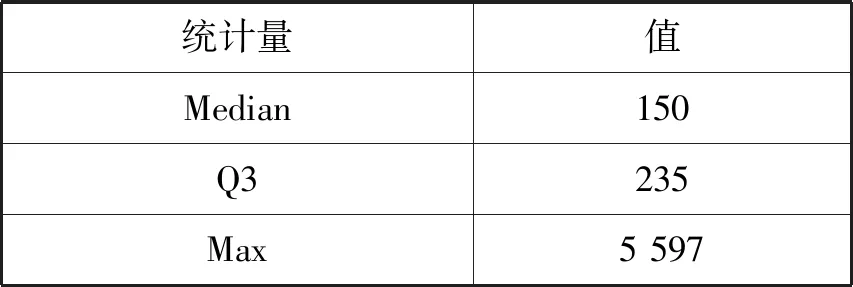
续表1
考虑到Crime count的数值不可能为负,根据表1信息和异常值截断点的计算方法,当Crime count>442.25或Crime count<0时为异常点。由此可以判断本数据集存在55个异常点,为了不影响回归分析采用暴力法直接删除异常数据,数据集剩余744条数据。删除异常数据后,本文使用R语言的mice包对缺失数据采用均值填充,并在填充的数据集上训练BP预测模型和PSO-BP预测模型。
3 PSO-BP神经网络模型
3.1 算法原理
3.1.1粒子群优化算法
粒子群优化(Particle Swarm Optimizer, PSO)算法最早发端于人对鸟群捕食行为的观察与研究,即假设一群鸟在随机地寻找食物,然而搜索区域内只有一块食物,并且所有的鸟都不知道食物的方位,但能判断自己的位置与食物的距离。在鸟群中信息是共享的,每只鸟都会与其他鸟共享自己与食物的距离,所有鸟都会跟随距离食物最近的那只鸟寻找食物,这蕴含着鸟类的社会行为和个体认知行为。
PSO算法正是从这种模型中得到启发,优化问题的每一个可行解都被看作一只鸟,被称为“粒子”,每只鸟都在一个d维空间中寻找最优解,每个粒子的当前位置与最优解的距离由适应度函数来确定,即为适应值,每个粒子都有一个飞行速度,决定粒子飞行的速度和方向。
3.1.2BP神经网络
BP神经网络是一种多层前馈神经网络,主要特点是信号前向传播,误差反向传播。信号前向传播是指信号从输入层经过隐藏层处理,再经过非线性变换,传至输出层,如果输出层的输出与期望输出不相符,则计算误差并将误差进行反向传播。误差反向传播是指误差经过输出层,再到隐藏层,最后到输入层,各层各个神经元根据误差信号调整权重和阈值,直至BP神经网络的误差达到预设的值,或迭代次数达到最大迭代次数,使得预测输出不断逼近期望输出。常见的三层BP神经网络拓扑结构如图2所示。
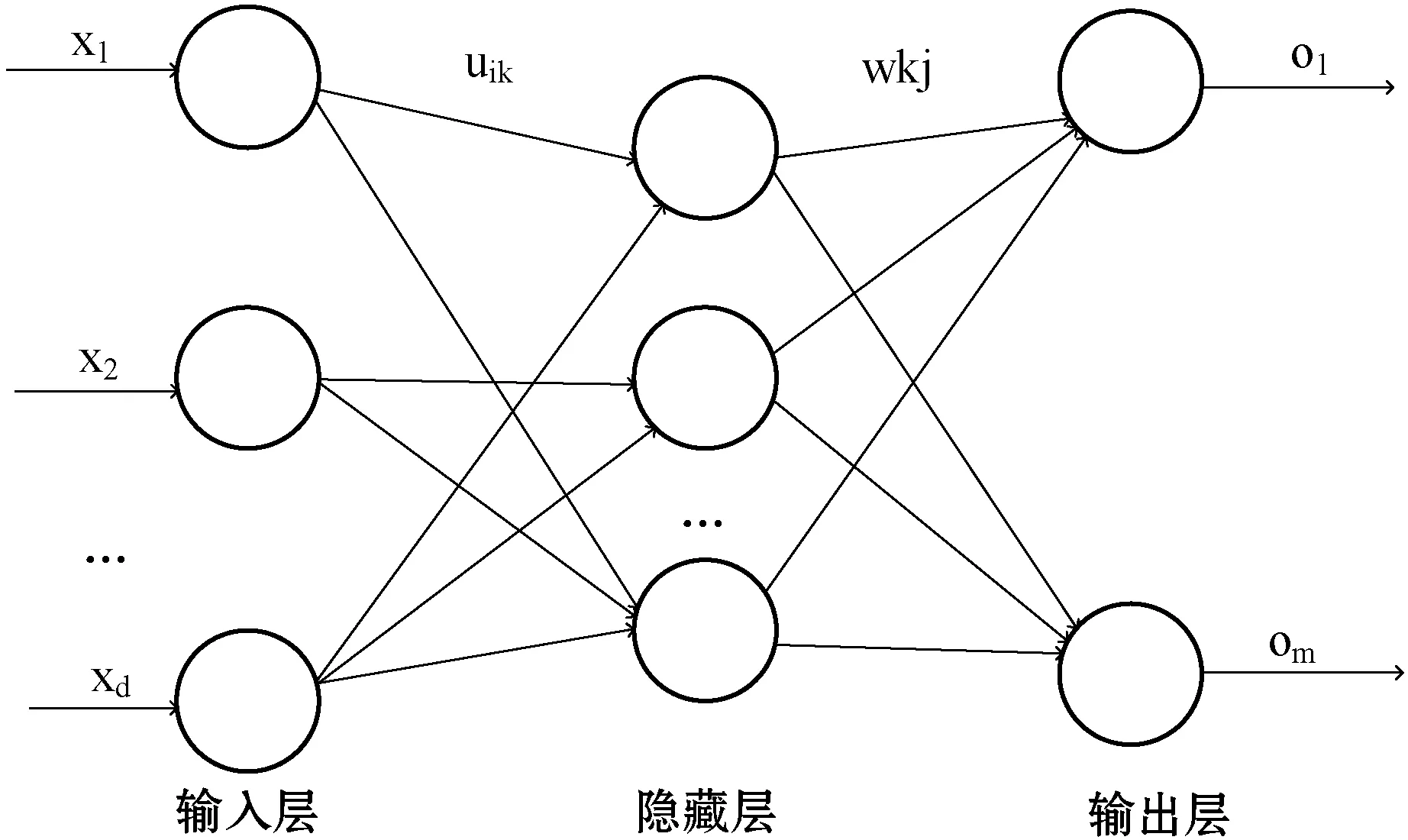
图2 BP神经网络拓扑结构图
在图2中,x1,x2,…,xd是BP神经网络的输入值,输入层的节点个数一般为训练数据集的维度。O1,O2,…,Om是BP神经网络的输出值,uik和wkj分别是BP神经网络中输入层与隐藏层的权重和隐藏层与输出层之间的权重。事实上,BP神经网络可以看成一个非线性函数,网络输入值和输出值分别为该函数的自变量和因变量。当输入节点数为d、输出节点数为m时,BP神经网络表示从d个自变量到m个因变量的映射关系。如果O是离散值且m>2,则BP神经网络可以解决多分类问题;如果O是离散值且m=2,则BP神经网络可以解决二分类问题;如果O是实数值,则BP神经网络可以解决回归问题。
BP神经网络在处理多个输入变量的数据上表现良好,而且具有结构简单,便于实现,且在数据量较少情况下能够获得较高的精度,但是由于初始权重是随机产生的,极易陷入局部最优解。
3.2 PSO-BP神经网络算法
本文基于粒子群优化算法,结合BP神经网络的权重更新算法,寻找最佳的网络连接权重和阈值。首先将BP神经网络连接权重和阈值进行粒子化,一般将BP神经网络的连接权重uik、wkj和阈值a、b拼接成为粒子的位置向量。设BP神经网络的输入层、隐藏层及输出层的节点数分别为d、l、m,则第n个粒子的位置向量为:
posn=(pn1,pn2,…,pnN)=(u11,…,uld,w11,
…,wlm,a1,…,al,b1,…,bm)
(1)
式中:N=dl+lm+l+m,uik表示输入层节点i与隐藏层节点k的网络连接权重,wkj表示隐藏层节点k与输出层节点j的网络连接权重,k=1,2,…,l;j=1,2,…,m。粒子的适应度计算公式如下:
(2)
式中:N为训练样本个数,Oik、yik分别表示粒子i确定的BP神经网络输出层的预测输出和期望输出。
由于每个粒子能够唯一确定一个神经网络,因此粒子位置的更新对应着BP神经网络权重与阈值的更新。基于粒子群优化算法的BP神经网络正是利用这种粒子位置的更新过程来搜索最佳的网络连接权重和阈值,从而达到BP神经网络训练的目的。
在PSO-BP神经网络中,本文采用sigmoid作为激活函数,算法流程如下:
Step1初始化。
初始化网络输入层节点数d、隐藏层节点数l,输出层节点数m,初始化隐藏层阈值a,输出层阈值b,设置学习速率η和激励函数f等参数。
初始化粒子群,包括粒子群的规模M,粒子n的位置向量posn=(posn1,posn2,…,posnd)和速度向量vn=(vn1,vn2,…,vnd),个体极值pbestn=(pn1,pn2,…,pnd)与群体的全局极值gbest=(pg1,pg2,…,pgd),最大迭代次数itmax及迭代误差精度ε等,其中n=1,2,…,M。
使用训练集对算法模型进行训练,当f(gbest)<ε或迭代次数t Step2利用如下BP神经网络权重更新公式对网络连接权重uik、wkj和阈值a、b进行更新。 (3) (4) ak=ak-ηδik (5) bj=bj-ηδkj (6) Step3将权重uik、wkj和阈值a、b拼接并粒子化,对每个粒子计算其适应值,得到粒子n的个体极值pbestn与群体的全局极值gbest,粒子化公式如式(1)所示,n=1,2,…,M。 Step4利用如下粒子群算法位置更新公式对各个粒子的位置进行更新。 (7) (8) γ=γmax-(γmax-γmin)t/itmax (9) Step5利用式(2)计算粒子群各粒子的适应度,寻找粒子个体极值pbestn和群体全局极值gbest。 Step6输出粒子群全局最佳位置gbest及其确定的BP神经网络连接权重和阈值。 综上,本文提出的改进算法结合了PSO优化算法与BP神经网络的优化过程。首先采用PSO优化算法对BP神经网络的随机初始权重进行全局寻优,并将全局优解作为BP神经网络的初始权重,然后采用PSO优化算法和BP神经网络对权重进行交替更新,即在每一次的迭代过程中先采用BP神经网络对权重进行初步更新,再采用PSO优化算法对权重进行再次优化。这样既利用了PSO优化算法的全局搜索能力,又充分体现了BP神经网络的误差反向传播的特点,实现了从全局搜索BP神经网络的权重最优解,使BP神经网络有了动态学习的能力,解决了BP神经网络易陷入局部最优解的问题。 目前国外对于美国犯罪问题的研究普遍采用的解释变量为贫困率、单亲家庭数、房价中位数、人种、就业率等[13]。因此,本文也根据United states census网站上提供的该市每个人口统计区的房价中位数(House price)、贫困率(Poverty percentage)、女性(单亲)户主数(Female household)、总人口数(Total population)、白人人口数(White)、黑人或非裔美国人数(Black or Africa)、亚裔美国人数(Asian)、本科率(Bachelor degree)、劳动参与率(Labor force)、新建(改建)房屋许可数(Permit)、统计区内各犯罪点到最近警务站的平均距离(Distance)等十一类数据,作为影响因子进行分析。如表2所示,House price属性有10个缺失值,缺失率为1.34%,缺失率较低,其余变量缺失值均为0,本文使用R语言的mice包对缺失数据进行平均值填充。 表2 数据集详细信息 经过异常值处理和缺失值处理后,本文使用R语言的rattle包对各个属性与一般盗窃犯罪数量Crime count的相关性进行分析。在相关性分析时采用Pearson系数衡量两个变量的相关度,为了消除数量级的影响,先将数据使用平均数方差法进行标准化处理,再做相关性分析,属性之间的相关性分析结果如图3所示。 图3 相关性分析结果 图3中,两两属性之间可以用圆圈大小和颜色来表示相关性的强度,圆圈越大、颜色越深说明相关性越高,正值表示正相关,而负值则表示负相关。可以看出,房价(Houseprice)和白人人口数(White)与一般盗窃犯罪数量(Crimecount)的相关性最弱,而黑人或非裔美国人数(Black or Africa)、女性(单亲)户主数(Female household)以及新建(改建)房屋许可数(Permit)与该类犯罪数量的正相关性最强。 在对犯罪数量进行预测时,将数据集采取7:3随机划分,取70%的数据为训练集,30%的数据为测试集,训练集中Crimecount的描述性统计量如表3所示。 表3 训练集中Crimecount的描述统计量 在训练预测模型之前,首先对数据进行归一化处理,在建立BP神经网络模型时,隐藏层节点设为12,训练次数为1 000,学习率η=0.01,激活函数为‘tansig’;在建立PSO-BP神经网络时,隐藏层节点数设为3,训练次数1 000,激活函数为‘tangisg’,粒子群规模40,粒子飞行速度最大为0.5,wmax=0.9,wmin=0.3,c1=2,c2=1.8,a=-1,b=1,r1=r2=1。 分别根据之前介绍的BP神经网络模型训练方法和PSO-BP神经网络模型训练方法,训练犯罪数量预测模型。训练得到PSO-BP神经网络从输入层到隐藏层的权重及阈值如表4所示,隐藏层到输出层的权重及阈值如表5所示。 表4 输入层到隐藏层权重及阈值 表5 隐藏层到输出层权重及阈值 以表6所示的5个样本为例,将数据送入输入层,首先需要归一化处理,然后根据权重uik和阈值ak进行加权求和并经过隐藏层的激励函数进行计算并输出,隐藏层的输出数据作为输出层的输入数据,并经过输出层的权重wkj和阈值b进行加权求和,最后进行反归一化处理并作为输出层的输出数据,即为样本的预测犯罪数量(对应于表6中的Predicted Crimecount行),表6所示样本的真实犯罪数量为True Crimecount行。 表6 样例及PSO-BP预测结果 采用上述实验方法和参数设置对训练集进行预测模型训练,得到预测模型后,对测试集进行预测,并对结果进行反归一化处理。真实值与BP预测值、PSO-BP预测值的对比结果如图4所示,可以看出,PSO-BP模型的预测值与实际值比较接近。 图4 犯罪数量预测结果对比 图5给出了应用BP神经网络模型和PSO-BP神经网络模型预测的各人口统计区犯罪数量的平均绝对值相对误差EMAPE,计算公式如下: (10) 式中:yj、Oj分别为第j人口统计区实际犯罪数量和预测数量。 图5 预测结果相对误差对比 图5中有很多误差“尖峰”,这些点的出现直接影响了预测的整体效果,目前国内外学者对“尖峰”的研究较少,主要是这些“尖峰”产生的原因非常复杂,规律性差,很难预测。但与BP神经网络相比,PSO-BP预测的相对误差相对较小。 表7给出了两种模型的平均EMAPE值的对比分析,相较于BP神经网络模型,PSO-BP神经网络模型的预测精度具有明显提高。 表7 两种模型的平均相对误差 本文针对BP神经网络对初始权重敏感,容易陷入局部最优解的问题,引入PSO优化算法,对网络权重进行全局搜索,同时采用BP神经网络权重更新方法对PSO搜索到的权重和阈值进行进一步更新,构建PSO-BP神经网络模型,对犯罪数量进行预测。在744个人口统计区的犯罪数据集上的实验结果表明,基于PSO-BP神经网络算法的犯罪数量预测模型的预测精度有明显提升,在该一般盗窃犯罪的数量预测中有良好的应用效果。
4 一般盗窃犯罪影响因素分析及数量预测
4.1 影响因子选取
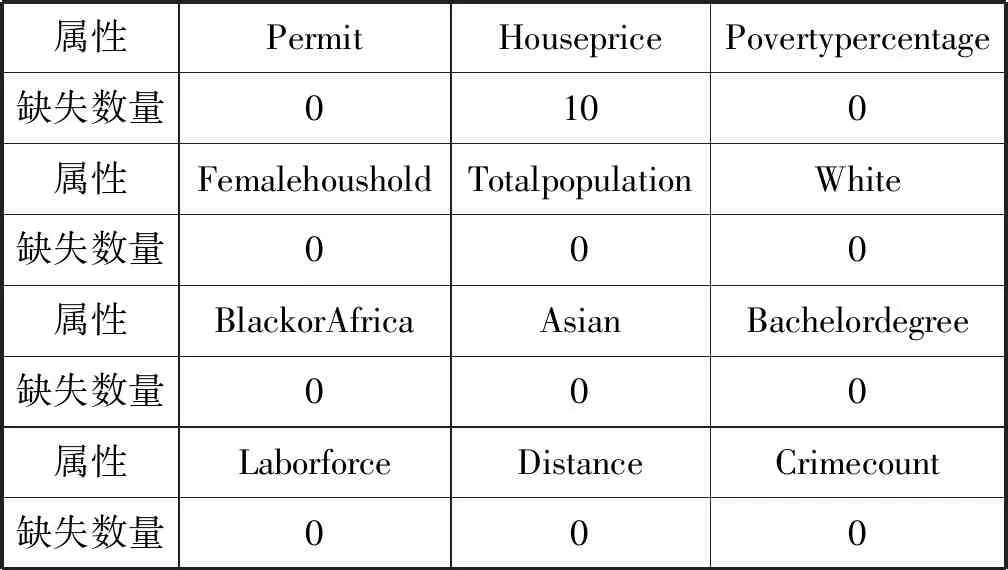
4.2 犯罪数量影响因子分析
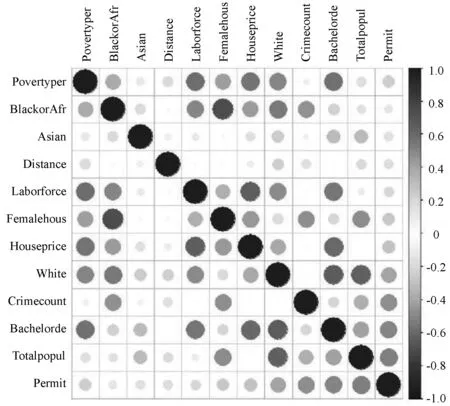
4.3 实验方法及参数设置
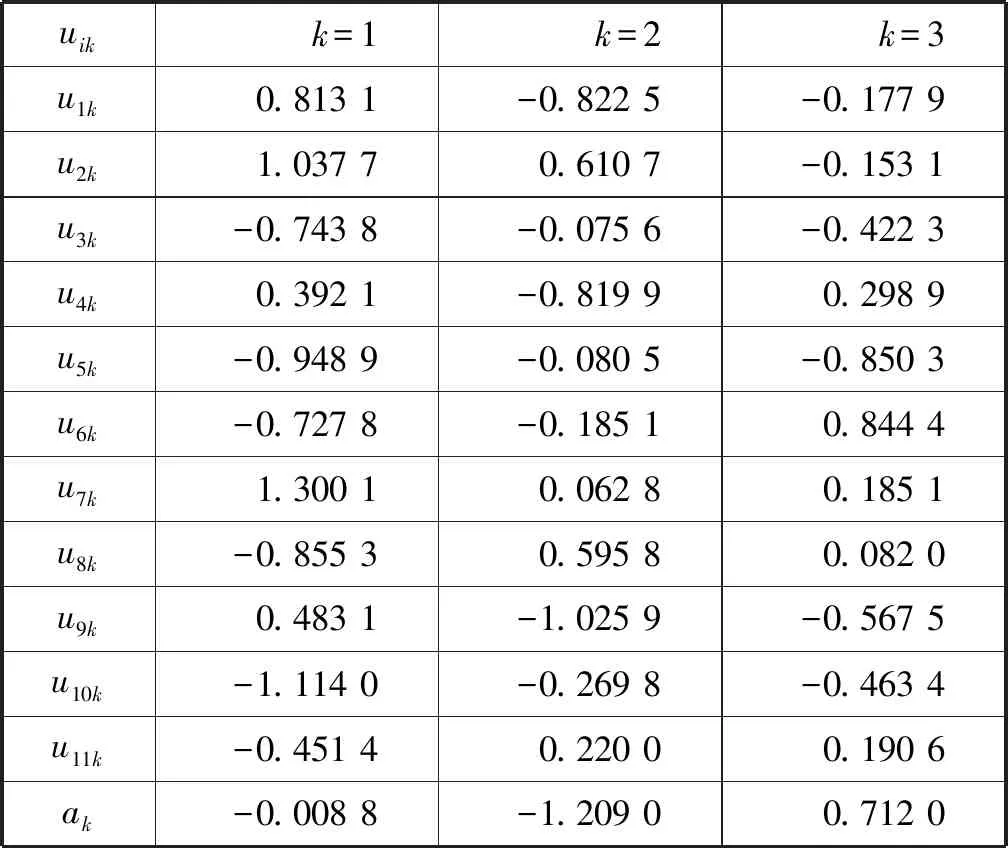

4.4 预测结果与评价

5 结 语

