基于本体的疾病关联搜索方法的研究

梅 祎， 王亚东

(哈尔滨工业大学 计算机科学与技术学院， 哈尔滨 150001)

0 引 言

近年来，随着医疗技术和生物科技的迅猛发展，生物领域的大数据急剧增加。其中，疾病本体和其它相关的数据如药物、基因及相关文献等是生物大数据中不可或缺的典型组成部分。随着数据量规模的日趋庞大，数据的快速、有效检索成为了至关重要的研究问题。

然而，主流的综合搜索引擎如百度、Google等对疾病关键词的检索结果普遍来说都比较简单通俗，偏向科普的形式，适用于并不具备专业知识的普通用户，因而不能满足更高层面的研究需求，尤其是对专业的医疗工作者和研究者来说，搜索结果也尚未臻至专业和全面。

面向疾病领域的垂直搜索引擎不仅数目稀少，而且功能单一。例如，疾病浏览器Disease Ontology(http://disease-ontology.org)，虽然搜索结果是有效的，但搜索结果未能按照相关性的大小给出有序展示，且包含的知识不够丰富，对用户来说，从其中提取自身想要的信息还需做进一步的筛选，是一个耗费时间和精力的过程。

基于此，本文提出了基于疾病本体的关联搜索，关联检索算法综合考虑了疾病本体及其相关数据之间的关联，为用户提供有效的检索信息，结果表明，关联搜索算法的搜索结果相关度高、内容丰富，此外，用户还可以根据个人的偏好，或者行为习惯，通过调整参数，修改搜索结果出现的先后顺序。

1 相关工作

搜索引擎主要分为2种：综合搜索引擎和面向专业领域的垂直搜索引擎[1-2]。 对此可阐释解析如下。

(1)综合搜索引擎[3]。现在已经得到了广泛的研究。其中，Google公司提出的PageRank算法[4]，即是依靠网页之间的链接关系来确定每一个页面的等级,一个页面到另一个页面的链接可解释成该页面对另一页面的投票，PageRank算法根据这些投票来源和投票目的的等级确定新的等级。PageRank算法在普通的网页搜索中表现得较好，但是涉及到专业领域的搜索时，往往没有很好的结果。除了PageRank之外，HITS也是常用的链接分析技术[5]，是用于分析网页重要性的设计算法，可根据一个网页的入度(指向此网页的超链接)和出度(从此网页指向别的网页)来衡量网页的重要性。其最直观的意义就是如果一个网页的重要性很高，则由其所指向的网页的重要性也会较高。一个重要的网页被另一个网页所指，则表明指向该网页的重要性也会很高。指向别的网页定义为Hub值，被指向定义为Authority值。

(2)垂直搜索引擎。即专业或专用搜索引擎，就是专为查询某一学科或主题的信息而产生的查询工具，专门收录一方面、某一行业或某一主题的信息，与搜索引擎门户相比，对解决实际查询问题要更加有效[6]。

2 方法

2.1 问题描述

在由不同类型的数据构成的数据集合中，数据之间存在着各种相关关系，比如疾病本体之间的父子及兄弟关系，疾病与药物、基因等数据之间的关联关系等。因此，这些数据组成了一个复杂的异构网络，每一个数据条目都可以对应成网络中的一个节点，数据间的关系对应节点间的边。

本课题所需要实现的目标是在这个复杂的异构网络中，搜索出与待搜索关键词相关度最高的前n个节点。

2.2 知识库建立

本课题首先建立起了疾病本体及其相关数据包括基因、表型、药物、文献等数据之间的异构网络，研究使用的数据主要来自于选取医学数据库，该部分研究内容可探讨分述如下。

(1)Disease ontology[7]。疾病本体来自于开放生物医学体系(Open Biomedical Ontology，OBO)，是纪录了与人类相关疾病数据的本体库。

(2)MeSH(Medical Subject Headings)[8]。是美国国家医学图书馆创建的医学主题词表，由于其结构体系完整合理，在世界范围内被广泛使用。

(3)KEGG[9](Kyoto Encyclopedia of Genes and Genomes)数据库。是从分子水平，整合了基因、酶、化合物及代谢网络信息的综合性数据库。

(4)OMIM[10](Online Mendelian Inheritance in Man)数据库。是在线孟德尔人类遗传数据库，主要包括了遗传疾病、遗传表型及基因等信息。

(5)MEDIC(合成疾病词汇，merged disease vocabulary)[11]。是整合OMIM术语、同义词和标识符与MeSH术语、同义词、标识符、定义和层级关系的资源，通过MEDIC，就在原有基础上补充及丰富了数据间的关联关系。

2.3 方法设计

知识库网络可以表示为图G=(V,E),其中V为节点集合，E为边的集合，任意的2个节点之间用一条边连接，边的权值代表相似性或相关性，其取值范围为[0,1]。权值矩阵为M，对任意的节点v1,v2，称M(v1,v2)为节点v1和节点v2之间的固有相关度。

衰减系数用来表示从某一类型节点到另一类型节点之间相关性的衰减。设节点类型数量为N，则衰减系数可以表示为N×N的矩阵R。对∀v∈V，函数t(v)表示节点v的节点类型。对任意的节点v1,v2,R(t(v1),t(v2))表示节点v1和v2的衰减系数。

综合考虑节点间的相关性和节点类型间的衰减系数，得到一个大小为|V|×|V|的综合相关度矩阵S。计算方法为：

Si, j=Mi, j×Rt(i), t(j),i∈[1, |V|],j∈[1, |V|].

(1)

对于待查询的关键字k，可以将其视为一个特殊的节点，加入至上述网络。其与每个节点之间有一个直接的相似度，由指定的打分函数进行定义。将网络由此扩展后，新的网络可表示为一个(|V|+1)×(|V|+1)的矩阵W。

查询算法的目的是找到网络中与待查询关键字k相关性最高的n个节点，而该相关性不仅由该节点与待查询关键字节点之间的直接相关性决定，亦是由该节点周围的节点决定。下面，研究给出了查询问题的形式化定义。

定义1设vi,vi+1, …,vi+n为vi到vi+n之间的一条哈密顿通路，将W(vi,vi+1)×W(vi+1,vi+2)×…×W(vi+n-1,vi+n)称为节点vi和vi+n之间关于该条哈密顿通路的相关度。若该条通路记为p，将该路径相关度则记为Yp。

定义2设函数g(vi,vj)表示节点vi和节点vj之间的全部哈密顿通路。节点vi和节点vj之间相关度可以定义为节点vi和节点vj之间的全部哈密顿通路的相关度的最大值，设节点间的相关度为f(vi,vj)，则f(vi,vj)=max{Yp},p∈g(vi,vj)。当vi为待搜索的关键词节点k时，记f(k,vj)为f(vj)。

因此，问题可以被表述为输入待查询关键词k和查询数目n，输出集合Q，满足Q⊂V, |Q|=n, 且∀v′∈V-Q,v∈Q,f(k,v′)>f(k,v)(即输出分数前n的节点数组)。

在此基础上，研发得到了关联搜索算法的流程步骤可表述如下。

输入：查询的关键词k，查询数目n

输出：集合Q，满足Q⊂V, |Q|=n, 且∀v′∈V-Q,v∈Q,f(k,v′)>f(k,v)(即输出分数前n的节点数组)。

A←[]

B←[]

ForvinV:

v.score←W(k,v)

B.add(v)

B.sort

Forifrom 1 ton:

v←B.first

A.add(v)

B.remove(v)

forv' inB:

v'.score=max{v'.score,v.score*W(v,v')}

B.sort

returnA

2.4 算法正确性证明

考虑如下的命题：每次循环执行前，B数组的第一个节点v1满足f(v1)=v1.score，且不存在B数组中的其它节点vi，会使f(vi)>v1.score。下面,关于该命题的正确性证明过程详见如下。

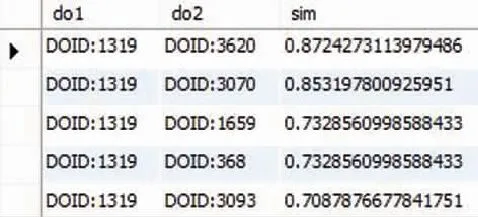
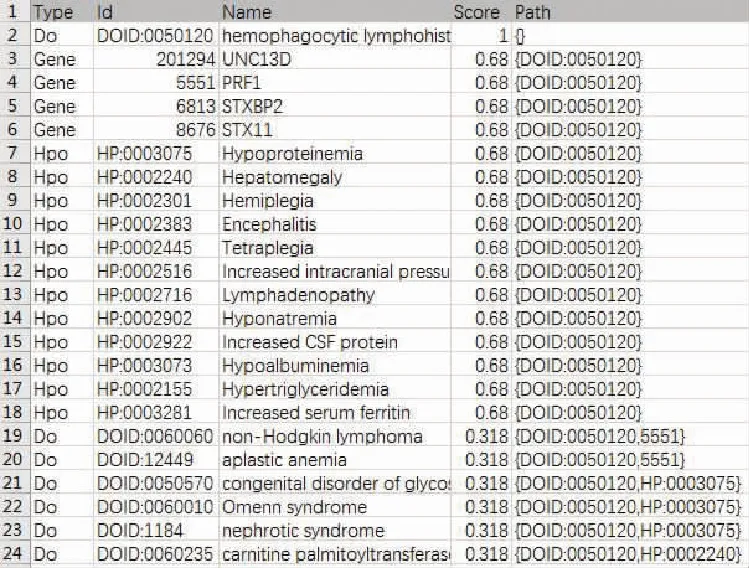
经过研究可知，循环第一次执行前，显然，vi.score=W(k,vi),而B数组中元素已经经过排序，因此W(k,vi)

由于该命题成立，使得算法每次从B数组中移除第一个节点，将其添加到A数组中，而当循环执行n次结束后，A数组中的节点是全部节点中分数从大到小排列的前n个元素。因此推得，算法是正确的。

2.5 算法复杂度分析

(1)算法的时间复杂度为：n×|V|×log(|V|)。

(2)算法的空间复杂度为：|V|2。

3 结果分析

以搜索“brain cancer”为例，可得搜索结果如图1所示。

图1 “brain cancer”的搜索结果图

从图1中可以看出，首先搜索得到与搜索关键词直接相关的疾病本体“DOID:1319”和“DOID:4203”。然后搜索出了其它关联的疾病本体，如“DOID:3620”，从路径中可以看出其是与疾病本体“DOID:1319”相关的，这2个疾病本体在疾病本体树中的结构如图2所示，分析得知“DOID:1319”是疾病本体“DOID:3620”的子节点。图3是计算后的疾病本体间相似度，由此推得，这2个疾病本体具有较高的相关度。

接下来，若以“0050120”作为搜索关键词，搜索的结果则如图4所示。从图4中可以看出，不仅搜索出了直接与关键词匹配的疾病本体“DOID：0050120”，还检索出了该疾病本体相关的基因及表型等。此外，研究中又发现，通过疾病本体“DOID:0050120”关联到了的基因“5515”再关联到疾病本体“DOID:0060060”，体现了这2个疾病本体关联着共同的基因，两者之间也存在着某种关联关系。

图2 疾病本体“DOID:1319”与疾病本体“DOID:3620”在树中的位置图

Fig. 2 The “DOID:1319” and “DOID:3620” in the tree of disease ontology

图3 疾病本体“DOID:1319”与其它疾病本体的相似度信息图

Fig. 3 The similarity of“DOID:1319” with other disease ontologies

图4 “0050120”的搜索结果图

4 结束语

本文针对疾病本体及其相关数据的检索问题，提出了基于疾病本体的关联搜索算法。首先，根据多种医疗数据库中的原始数据，构建异构知识网络，之后，设计了在知识网络中进行关联搜索的算法，算法可对节点与关键字之间的每条路径进行评分，并选取其中评分最高的路径作为该节点的最后得分，最终选取得分最高的若干个节点。结果表明，关联搜索算法不仅可以搜索出文本匹配方法能够搜索出的结果，而且能够搜索出其难于搜索得出、但却与关键词相关的结果。