含缓变未知输入的数据自校准滤波方法

傅惠民， 杨海峰， 付越帅， 崔 轶

(北京航空航天大学 小样本技术研究中心， 北京 100191)

0 引 言

目前，Kalman滤波(Kalman Filter,KF)已广泛用于人工智能、在线监测、故障诊断、导航与控制等工程领域[1]。众所周知，Kalman滤波要求状态方程和量测方程均精确，其可以有偶然误差而不能包含系统误差，但是在工程实际中，由于受到环境因素、模型和参数的选取不当、测量设备的不稳定性等影响，状态方程或量测方程中往往含有未知输入(系统误差)，这些未知输入在滤波过程中会严重降低滤波精度[2-4]。如何补偿和修正这些未知输入的影响，进一步提高Kalman滤波精度，是当前滤波领域的研究难点和热点问题。

为此，人们先后提出：

(1)自适应Kalman滤波方法(Adaptive Kalman Filter)[5]，但是自适应Kalman滤波误差大，甚至导致滤波发散；

(2)状态扩维估计方法(Augmented-state Estimation)，可通过将未知输入作为状态变量进行扩维估计，这既不准确、又徒增计算工作量[6]；

(3)鲁棒两步Kalman滤波方法(Robust Two-stage Kalman Filter)[7]，其本质是仅用不含未知输入的量测方程进行状态估计，但这已不属于Kalman滤波，因其无法通过状态方程和量测方程之间的融合来减小滤波的偶然误差。

傅惠民等人[8]通过建立相邻两次滤波之间未知输入的纵向联系和未知输入与状态变量的横向联系，提出了一种能够自动消除系统误差、减小偶然误差的自识别自校准滤波方法(Self-Recognition Self-Calibration Filtering Methods)，解决了干扰和噪声引起的未知输入(系统误差)问题，有效地提高了滤波精度。本文将进一步针对工程领域遇到的缓慢变化的未知输入(系统误差)问题，建立一种含缓变未知输入的数据自校准滤波方法，以简化计算，便于工程应用，适合边缘计算。

1 量测自校准滤波方法

1.1 线性量测方程

工程上，含未知输入的线性量测方程组一般形式为:

Yk=HkXk+dk+Vk,

(1)

式中，Xk为m维状态向量；Yk为n维量测向量；dk为n维量测未知输入(系统误差)向量；Hk为量测矩阵；Vk是均值为零，协方差矩阵为Rk的量测噪声向量，并且满足：

(2)

式中，E(·)为数学期望符号，δk, j为δ函数，当k=j时，δk, j=1，当k≠j时，δk, j=0。

1.2 未知输入自校准

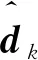
(3)

1.3 量测自校准滤波

在未知输入dk自校准估计完成后，可以对量测数据进行自校准滤波，基于加权最小二乘原理进行状态估计，可得：

(4)

状态估计对应的估计误差协方差矩阵为：

(5)

2 量测扩展自校准滤波方法

2.1 非线性量测方程

工程中，含未知输入的非线性量测方程组一般形式为：

Yk=hk(Xk)+dk+Vk,

(6)

式中，hk(·)为非线性量测函数；Xk，Yk，dk和Vk的意义与式(1)一致。

2.2 未知输入自校准

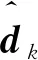
(7)

2.3 量测扩展自校准滤波

Yk=HkXk+Uk+dk+Vk,

(8)

式中，

(9)

(10)

线性化完成后，基于加权最小二乘原理进行状态估计，可得状态估计值和估计误差协方差矩阵为：

(11)

(12)

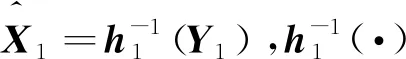
3 状态方程含未知输入自校准Kalman滤波方法

3.1 线性系统方程

工程上，状态方程含有未知输入的线性离散系统一般形式为：

Xk=Φk-1Xk-1+bk-1+Wk-1,

(13)

Yk=HkXk+Vk,

(14)

式中，Φk为状态矩阵；bk为状态方程中的未知输入；Hk，Xk，Yk的意义与式(1)一致；Wk是协方差矩阵为Qk的状态噪声向量；Vk是协方差矩阵为Rk的量测噪声向量，并且满足:

(15)

3.2 状态未知输入自校准

(16)

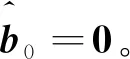
3.3 自校准Kalman滤波

当状态方程未知输入bk-1自校准完成后，可对线性系统进行自校准滤波，计算步骤如下：

(17)

一步预测误差协方差矩阵Pk/(k-1)为：

(18)

滤波初始化为：

(19)

(20)

(21)

状态估计误差协方差矩阵Pk为：

Pk=(I-KkHk)Pk/(k-1),

(22)

式中，Kk为滤波增益矩阵，由下式计算得到：

(23)

4 状态方程含未知输入扩展自校准Kalman滤波方法

4.1 非线性系统方程

工程上，状态方程含有未知输入的非线性离散系统一般形式为：

Xk=fk-1(Xk-1)+bk-1+Wk-1,

(24)

Yk=hk(Xk)+Vk,

(25)

式中，fk(·)和hk(·)均为非线性向量函数；Xk，Yk，bk，Wk，Vk定义与式(13)和(14)相同。

4.2 状态未知输入自校准

(26)

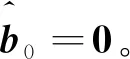
4.3 扩展自校准Kalman滤波

当状态方程未知输入bk-1自校准完成后，可按如下步骤进行非线性系统自校准滤波：

(1)一步自校准预测。非线性系统一步自校准预测为：

(27)

(28)

滤波初始化仍由式(19)和式(20)给出。

(29)

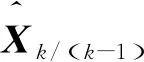
(30)

5 量测方程含未知输入自校准Kalman滤波方法

5.1 线性系统方程

工程上，量测方程含有未知输入的线性离散系统一般形式为：

Xk=Φk-1Xk-1+Wk-1,

(31)

Yk=HkXk+dk+Vk,

(32)

式中，Φk,Hk，Xk，Yk，Wk，Vk的意义与式(13)和(14)一致，dk的意义与式(1)一致。

5.2 量测未知输入自校准

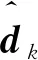
5.3 自校准Kalman滤波

当量测方程未知输入dk自校准完成后，可对线性系统进行自校准滤波，计算步骤如下：

(33)

一步预测误差协方差矩阵Pk/(k-1)由式(18)计算得到。

滤波初始化由式(19)和式(20)给出。

(34)

状态估计误差协方差矩阵Pk和滤波增益矩阵Kk分别由式(22)和(23)计算得到。

6 量测方程含未知输入扩展自校准Kalman滤波方法6.1 非线性系统方程

工程上，量测方程含有未知输入的非线性离散系统一般形式为:

Xk=fk-1(Xk-1)+Wk-1,

(35)

Yk=hk(Xk)+dk+Vk,

(36)

式中，fk(·)，hk(·)，Xk，Yk，Wk，Vk意义与式(24)和(25)相同，dk的意义与式(1)一致。

6.2 量测未知输入自校准

6.3 扩展自校准Kalman滤波

当量测方程未知输入dk自校准完成后，可按如下步骤进行非线性系统自校准滤波：

(1)一步预测。非线性系统一步预测为:

(37)

一步预测误差协方差矩阵Pk/(k-1)由式(18)给出，其中Φk-1仍由式(28)计算。

滤波初始化仍由式(19)和式(20)给出。

(38)

状态估计误差协方差矩阵Pk和滤波增益矩阵Kk分别由式(22)和式(23)计算，其中Hk仍由式(30)计算。

7 双未知输入自校准Kalman滤波方法

7.1 线性系统方程

工程上，状态方程和量测方程均含有未知输入的线性离散系统一般形式为:

Xk=Φk-1Xk-1+bk-1+Wk-1,

(39)

Yk=HkXk+dk+Vk,

(40)

式中，Φk,Hk,Xk，Yk，bk，Wk，Vk的意义与式(13)和(14)一致，dk的意义与式(1)一致。

7.2 双未知输入自校准

7.3 自校准Kalman滤波

当状态方程未知输入bk-1和量测方程未知输入dk自校准完成后，可对线性系统进行自校准滤波，计算步骤如下：

滤波初始化由式(19)和式(20)给出。

8 双未知输入扩展自校准Kalman滤波方法

8.1 非线性系统方程

工程上，状态方程和量测方程中均含有未知输入的非线性离散系统一般形式为:

Xk=fk-1(Xk-1)+bk-1+Wk-1,

(41)

Yk=hk(Xk)+dk+Vk,

(42)

式中，fk(·)，hk(·)，Xk，Yk，bk，Wk，Vk意义与式(24)和(25)相同，dk的意义与式(1)一致。

8.2 双未知输入自校准

8.3 扩展自校准Kalman滤波

当双未知输入bk-1和dk自校准完成后，可按如下步骤进行非线性系统自校准滤波：

滤波初始化仍由式(19)和式(20)给出。

9 仿真算例

考虑如下的线性系统:

(43)

状态初值X0=1，wk和vk分别对应方差Qk=1和Rk=9，状态方程未知输入bk-1的取值为：

bk-1=1.2+0.01(k-1).

(44)

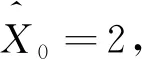
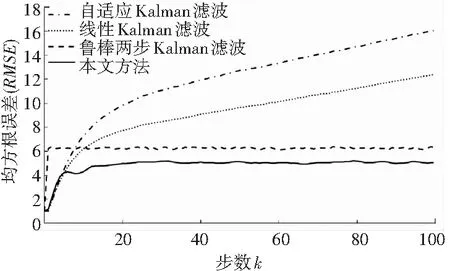
图1 均方根误差比较

表1 均方根误差均值比较

可以看到，当状态方程受到未知输入影响时，本文方法可以对其进行估计和补偿，其滤波精度比鲁棒两步Kalman滤波方法提高了22%，比线性Kalman滤波方法提高了47%，比自适应Kalman滤波方法提高了59%。

10 结束语

(1)由于工程实际中存在干扰和噪声，采集的信号往往含有缓慢变化的未知输入(系统误差)，Kalman滤波方法能够有效地减小偶然误差，但无法解决系统误差问题。本文方法则既能消除系统误差，又能减小偶然误差。

(2)量测自校准滤波方法和量测扩展自校准滤波方法，能够自动对量测数据中事先无法校准的系统误差进行估计、补偿和修正，从而减小系统误差的影响。

(3)状态方程含未知输入自校准Kalman滤波、量测方程含未知输入自校准Kalman滤波、状态方程和量测方程均含有未知输入的自校准Kalman滤波等方法，则能够自动对状态方程或量测方程中的未知输入进行估计、补偿和修正，从而提高滤波精度。

(4)理论分析、实例计算和仿真验证表明，本文方法能够对缓慢变化的未知输入进行补偿，消除系统误差，并通过数据融合减小偶然误差，比传统方法具有更高的滤波精度。并且计算简单，便于边缘计算和工程应用。

(5)对于工程实际中不知道有没有未知输入，但如果有的话必为缓慢变化的未知输入的情况，可以先采用文献[8]中自识别方法进行判断，然后再采用本文方法滤波。