单线简支箱梁车—轨—桥系统垂向振动分析

史耀君 （中铁第一勘察设计院集团有限公司，陕西 西安 710043）

1 引言

随着高速铁路的快速发展，铁路简支箱梁得到了广泛的应用，国内外学者针对双线简支箱梁进行了大量地、深入的研究，其设计、施工、养护技术已较为完善[1]，但对于单线简支箱梁的研究较少，对其梁高、竖向刚度等多项指标还未形成完整的理论体系；目前针对单线简支箱梁的研究主要有桂婞等[2]结合合蚌客运专线工程实际，编制了时速350km单线简支箱梁及桥墩参考图；孙大斌等[3]论述了盘营客专单线预制常用跨度简支梁的设计情况，包括主要结构尺寸拟定及结构构造、纵横向计算结果、车桥耦合动力仿真分析等内容，其研究结果表明，盘营客专单线简支梁截面尺寸在客运专线常用跨度简支梁中最小，但该参数简支梁经过试制，试验证明各项指标均满足设计及相关规定要求；杨鹏健[1]结合已建客运专线单线简支箱梁，分析了单线梁的梁高、桥面布置、腹板形式、梁端局部结构尺寸等的合理取值。

文章以高速铁路单线简支箱梁为例，建立列车-轨道-桥梁垂向耦合系统有限元模型，并采用MATLAB编制程序，着重分析了行车速度和桥梁垂向刚度对系统动力性能的影响。

2 车辆与轨道-桥梁结构振动模型

2.1 车辆模型

列车由若干节车辆组成，不考虑各节车辆之间的纵向作用，每节车辆模型由车体、2个转向架、4个轮对组成，其有限元模型如图1所示。

图1 车辆有限元模型

考虑车体和转向架的沉浮和点头位移，轮对仅考虑沉浮位移，则一节车辆模型有10个自由度，规定力和位移的方向以竖直向下为正，转角和力矩的方向以顺时针为正。

车辆位移列阵为：

2.2 轨道-桥梁模型

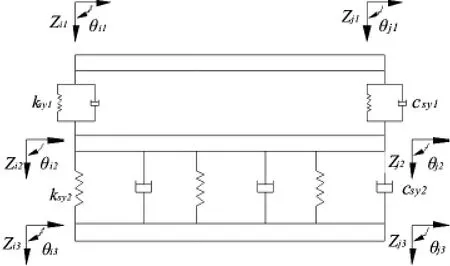
图2 板式轨道-桥梁单元模型

将板式无砟轨道-单线简支箱梁离散为若干个轨道-桥梁单元，见图2。在每一个轨道-桥梁单元中，钢轨和桥梁模拟为平面弹性点支承Euler梁单元，其左右节点编号分别为i1、j1和i3、j3；轨道板模拟为连续弹性支承平面梁单元，其左右节点编号分别为i2、j2；将扣件模拟为离散弹簧与阻尼器，砂浆层模拟为连续弹簧与阻尼器，刚度和阻尼系数分别用ksyi，csyi（i=1、2）表示。

轨道-桥梁单元的节点位移列阵为：

在任意一个轨道-桥梁单元内，钢轨内任意一点竖向位移可通过平面梁单元插值函数和节点位移参量表示为：

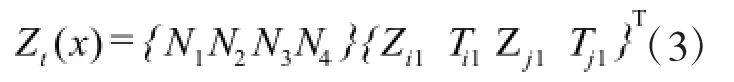
3 列车-轨道-桥梁系统垂向振动方程的建立及求解

3.1 非线性轮轨接触关系

根据非线性Hertz接触理论，第j位车轮的轮轨竖向相互作用力可由下式确定：

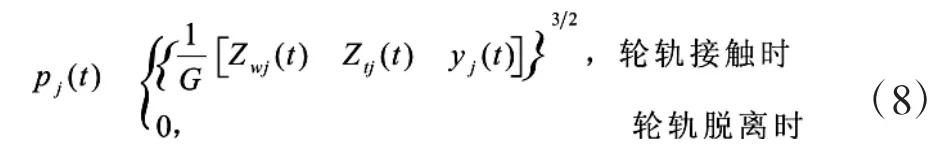
其中：G为轮轨接触常数；Zwj（t）为t时刻第j位车轮竖向位移；Ztj（t）为t时刻第j位车轮轮轨接触处的钢轨竖向位移；yj（t）为t时刻第j位车轮轮轨接触处的轨道不平顺。

轨道-桥梁单元等效节点荷载列阵为：

当轨道-桥梁单元无车轮作用时，Fe为12×1阶零列阵。

3.2 列车-轨道-桥梁系统垂向振动方程

运用弹性系统动力学总势能不变值原理及形成系统矩阵的“对号入座”法则[4]建立系统振动方程，并将轮轨非线性接触关系式（8）代入方程中，经整理可得车辆-轨道-桥梁系统垂向非线性振动方程为：

其中，FV（t）和 FT（t）为列车和轨道 - 桥梁之间相互作用力的关系；n为列车中车辆的节数分别为列车位移、速度与加速度列阵分别为轨道-桥梁位移、速度与加速度列阵；MV、KV、CV和MT、KT、CT分别为列车系统与轨道-桥梁系统的总体质量、刚度、阻尼矩阵；式（11）表示按“对号入座”法则组装矩阵，而不是数学上的矩阵相加[4]。

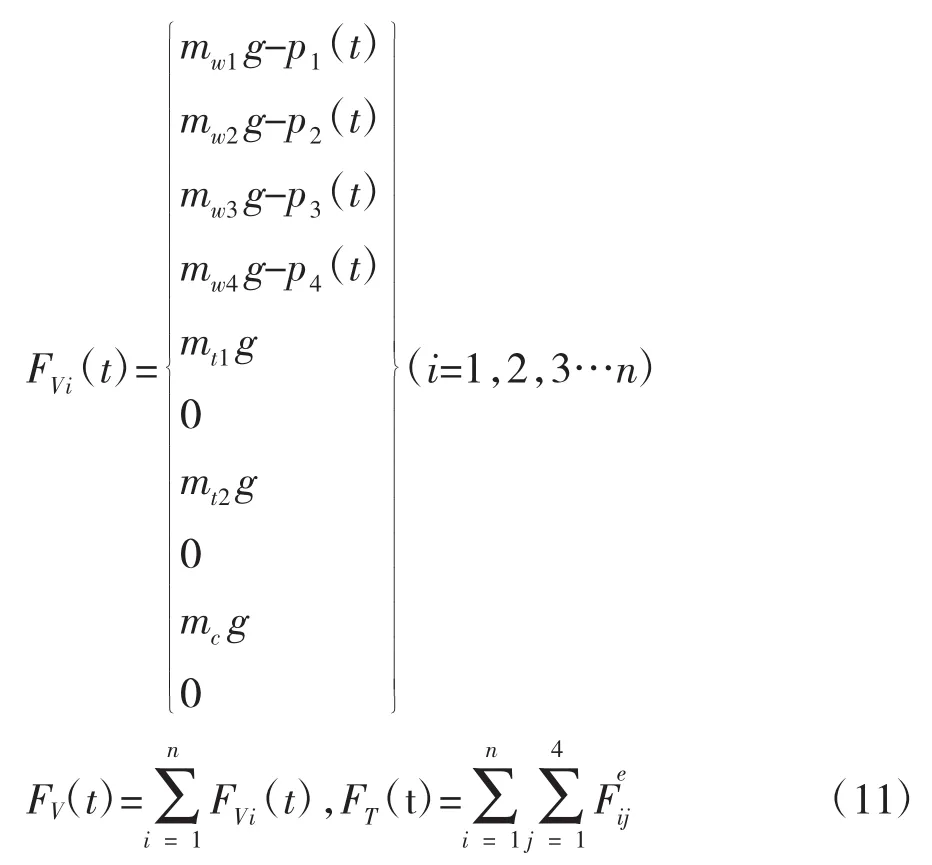
轨道-桥梁总体阻尼矩阵包括轨道本身的材料阻尼和轨下弹簧-阻尼器单元阻尼[4]：

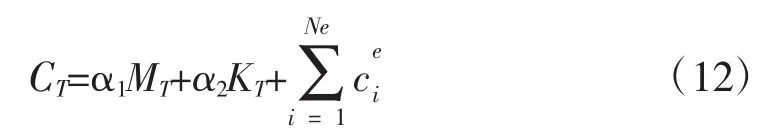
其中：α1，α2为瑞利阻尼系数，Ne为具有单元阻尼的单元数目为第i个弹簧-阻尼器单元的阻尼矩阵。

列车-轨道-桥梁非线性耦合动力方程求解采用交叉迭代算法，将列车-轨道-桥梁系统分解为列车子系统和轨道-桥梁子系统，分别独立求解列车和轨道-桥梁系统在不平顺激励作用下的动力响应U（t），。求解时通过轮轨接触力的平衡条件和位移协调条件来判定迭代是否满足收敛要求。

4 数值算例

文章以9跨高速铁路单线简支箱梁[7]为例，车辆模型采用CRH3高速列车，编组为（1M+6T+1M），轨道为CRTSII型板式无砟轨道，轨道不平顺采用德国低干扰轨道高低不平顺谱基于频域功率谱等效法模拟的轨道不平顺样本，根据文献[8]的研究，钢轨单元长度为2倍扣件长度时，既可以保证计算精度又能缩短计算的时间，故本次计算中轨道-桥梁单元长度取为1.3m，为消除边界效应对系统响应的影响，只考察中间5跨简支梁的响应。

图3所示为列车-轨道-桥梁垂向非线性耦合系统在轨道高低不平顺随机激励作用下系统加速度响应的时程曲线。从图中可以看出，最后一节动车车体加速度最大值为0.652m/s2，中跨跨中节点垂向加速度最大值为0.253m/s2，均满足设计规范要求[9]，表明该单线桥梁垂向刚度满足列车运行的刚度要求。

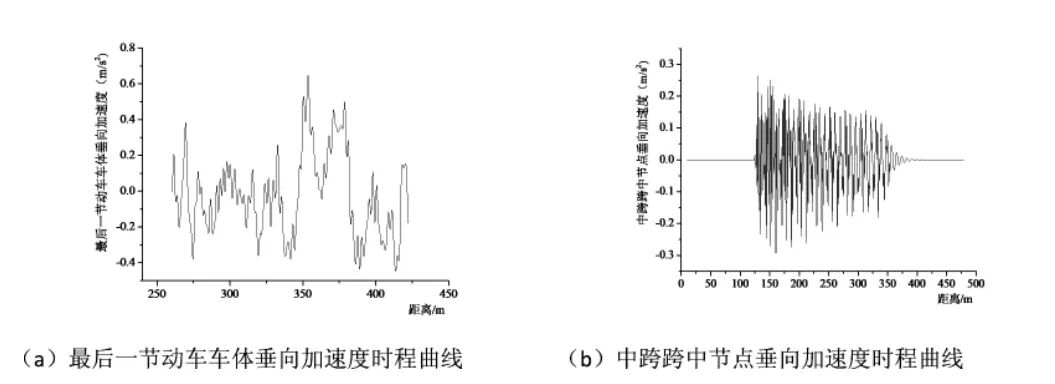
图3 系统加速度响应时程曲线（v=350km/h）

4.1 行车速度及桥梁垂向刚度影响分析

桥梁结构在运营过程中，由于混凝土劣化、徐变、钢筋锈蚀等一系列不良因素，其垂向刚度不可避免的会减小，为此文章基于列车-轨道-桥梁垂向耦合系统，分析梁体垂向刚度为原始刚度的1/5，2/5，3/5，4/5，6/5 时列车以不同速度运行条件下系统响应最大值的变化规律，其中下表为不同刚度条件下桥梁结构垂向基频及ZK静活载作用下桥梁跨中节点垂向位移对应的挠跨比。

《高速铁路设计规范》[8]规定高速铁路单线简支箱梁竖向挠跨比限值在ZK静活载作用下取双线简支梁限值的0.6倍，即单线简支梁挠跨比限制为1/2667，另该根据规范可得32m简支箱梁垂向自振频率下限值为3.05Hz。结合以上规范条文及下表计算结果可得：单线简支箱梁垂向结构刚度与原始刚度之比大于等于2/5时，满足规范对垂向基频和静活载挠跨比的要求。

不同刚度下挠跨比表

由图4（a）（b）可得，桥梁跨中节点垂向位移和垂向加速度受桥梁垂向刚度影响较大，跨中节点垂向位移和垂向加速度均随着梁体刚度的减小而增大，在同一刚度条件下，跨中位移和加速度随着行车速度的增大而增大，但在某些条件下垂向位移和加速度则出现明显峰值。这是因为周期性车辆荷载作用频率为桥梁自振频率的倍数，使得桥梁产生了共振作用。计算可得到桥梁结构刚度为原始刚度的1/5、2/5、3/5时对应的桥梁理论共振速度分别为 204km/h、287km/h、354km/h，这些峰值点与图（a）和（b）的计算结果吻合。另外，当2/5结构垂向刚度与原始刚度之比3/5时，满足规范要求，但其对应的共振速度与列车行车速度较为接近，系统动力响应会急剧增大，在设计时应根据设计速度合理选择桥梁刚度，以避开桥梁共振。

图4 列车-轨道-桥梁系统响应最大值随梁体垂向刚度变化关系

由图4（c）（d）可知桥梁垂向刚度对车体垂向加速度和轮轨垂向赫兹力影响较小，在相同梁体刚度时，二者均随着行车速度的增大而增大，在梁体刚度满足规范要求时，车体垂向加速度和垂向赫兹力均为明显变化。

5 结论

①桥梁垂向刚度对系统动力响应影响较大，当刚度不足时，系统响应会急剧增大，当刚度在规范要求的范围内时，系统响应主要受行车速度影响。

②桥梁垂向基频满足规范要求的下限值时，并不能有效的避开车桥共振区，在实际设计过程中，应结合车-轨-桥动力耦合模型，合理选择桥梁刚度。