锆自辐射损伤的分子动力学模拟与缺陷判定研究

钟 睿, 付宝勤, 崔节超, 侯 氢

(四川大学原子核科学技术研究所 辐射物理及技术教育部重点实验, 成都 610064)

1 引 言

由于中子和锆靶原子的弹性碰撞截面很小,发生相邻两次弹性碰撞事件距离在厘米量级,而级联碰撞影响区域在纳米量级， 所以载能中子致材料辐射损伤的模拟一般分为两个独立的模拟过程[1]. 首先是中子在材料中输运的模拟计算,以获得反冲原子能谱及其空间分布. 就如崔振国等[1]在其研究中指出的,1 MeV的中子在锆材料的靶材中产生的大部分PKA的能量都分布在1～15 keV之间,不同PKA的空间分布大多在6～8 mm之间. 其次再根据反冲原子能谱抽样计算各反冲原子能量下的级联碰撞过程. 本文涉及的是后一个过程,即级联碰撞过程的分子动力学模拟计算.

目前模拟原子级联碰撞过程最广泛采用的方法是以二体碰撞理论为基础的蒙特卡洛模拟方法[2-4]. 相应的代表性程序包有广为人知的SRIM等. 不过这种基于两体碰撞近似的模拟不能考虑级联碰撞过程中空位对离位原子的再捕获,因此对级联碰撞过程更精确仔细的模拟需要采用分子动力学模拟. 虽然随着计算技术的发展分子动力学已被越来越多地应用于材料损伤过程的研究[5-17],但如何用分子动力学模拟足够样本量的级联碰撞过程,并从中自动提取需要的统计物理量仍是值得仔细研究的问题.

与BCC等结构的金属相比较,关于锆级联碰撞的分子动力学模拟报道相对较少[18-22],其中比较有代表意义的包含,1998年Wooding等[19]采用Finnis-Sinclair势函数研究了PKA能量En达到20 keV时在Zr中产生的损伤,并指出Frenkel-pairs的数量和En呈一种幂相关性. 2001年Gao等[20]采用Ackland势函数研究了温度在100～600 K范围内Frenkel-pairs数量以及自间隙原子团簇随温度的变化情况. Voskoboinikov等[22]还研究了Zr金属Frenkel-pairs的数量和团簇形式与温度和PKA能量的相关性. 文献[1]报道了锆中级联碰撞的分子动力学模拟结果,但是PKA能量限于10 keV以下能区. 另外,文献[1]在计算离位原子数方面,靶原子相对其初始位置的位移量超过一个阈值则计入离位原子,由于没有考虑这些靶原子可以被其他离位原子留下的空位捕获,因此会高估离位原子数.

本文采用分子动力学模拟了10～50 keV能区的初级反冲原子在HCP结构Zr中的原子级联碰撞,并从方法学层面着重于考察了三种方法对点缺陷判定的影响. 结果表明,一种以Wigner-Seitz(WS)原胞分割为基础的判定方法更适合用于Zr在初级辐射损伤中产生的缺陷数统计. 该结论对于如何精确评估中子在Zr中产生的辐照损伤有指导意义. 此外,本文还研究了根据WS分割方法确定的自间隙原子点缺陷的迁移特征.

2 物理模型与分析方法

2.1 物理模型

本文采用分子动力学方法模拟Zr原子自辐射产生的级联碰撞,并通过统计级碰撞产生的点缺陷数来研究Zr受到辐射后的损伤程度. 其中,PKA能量范围设置为10～50 keV. 针对不同PKA能量,模拟体系采用不同原子数的盒子以提高计算效率. 盒子大小的选择依据是,级联碰撞主要影响区域不能因周期性边界条件出现重叠(击穿盒子),否则会造成晶体缺陷数减少[12]. 研究中,10～30 keV条件下模拟盒子包含原子数为414 720、 810 000和1 399 680;40和50 keV条件下包含原子数为6 480 000.

观察组：男、女占比各为26：19；年龄段在49～83岁之间，经计算后中位年龄为（66.21±1.34）岁。

分子动力学模拟采用Mendelev提出的Zr-Zr势函数[23],并采用了经过GPU算法优化的MD程序包MDSCU[24]以提高模拟计算速度. 每种PKA能量并行模拟5次. 模拟盒子温度设置为300 K,热量耗散采用声电耦合(E-P coupling， EPC)方法[25]. PKA随机选择入射角度. MD模拟采用自适应时间步长,保证运动最快的原子在一个时间步内的位移不能超过0.01a0(a0为锆晶格常数). 同时,每1 000步记录并输出一次分子动力学模拟结果.

此外,自间隙原子扩散研究方面,采用6 481个原子的盒子,并行模拟1 000次,模拟时间30 ps,记录时间间隔0.5 fs.

2.2 分析方法

根据分子动力学模拟产生的原子运动轨迹,本文比较了3种判定和计算间隙原子及空位的方法.

方法一,离位原子判定方法. 离位原子判定方法在蒙特卡洛模拟中使用较多,用于评估不同能量PKA造成影响的程度. 具体如图1a所示. 图1a中标记“1”和“2”分别表示一个原子的初始位置和当前位置,R表示位移距离. 当R值超过设定阈值,则该原子就被判定为离位原子,而并不考虑空位对间隙原子的捕获情况. 本研究中设定R=1a0,a0为Zr晶体晶格常数.

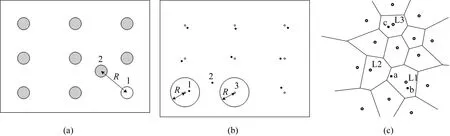
图1 点缺陷判定方法Fig.1 Point defects identification methods

图方向可视化结果(a=0.1 ps; b=1 ps; c=3 ps; d=10 ps)Fig.2 Visual result of cascade, direction (a=0.1 ps; b=1 ps; c=3 ps; d=10 ps)

方法二,传统间隙原子及空位判定方法. 该方法以计算原子和晶格格点之间的距离为基础,具体实现如图1b所示. 图1b中小圆环为晶体格点位置,实心圆点为原子位置. 以每个格点位置为球心设置半径为R的范围,若原子落入此范围内,被判定为普通原子,如标识“1”所示. 若原子不落入任何一个格点的R范围内,则被判定为间隙原子,如标识“2”所示. 若一个格点的R范围内无任何原子,则该格点位置被判定为空位,如标识“3”所示. 根据算法描述,通过该方法获得的间隙原子和空位数不一定匹配,即不一定都能构成Frenkel-pairs. 此外,采用该方法还需要考虑阈值R设定对判定结果的影响.

方法三,Wigner-Seitz (W-S)原胞分割方法. W-S原胞在空间上可以认为是以格点位置为中心点的Voronoi分割. 完备晶格中每个原胞中包含一个格点,若某原子在此原胞中,则该原子距离所在原胞格点的距离比其它原胞都短. 以此为依据,该判定方法如图1c所示. 图中小圆环为格点位置,实心圆点为原子位置. 判定时首先计算每个原子和所有格点的距离,设定每个原子“归属”距离其最近的格点,并判定如下:(1)若只有一个原子“归属”某个格点,判定为正常情况. 如图中标识“c”所示原子和“L3”所示格点位置关系. (2)若多于一个原子“归属”某个格点,则该格点存在间隙原子. 本文定义此格点位置为LSIA(location of self-interstitial atoms). 如图中标识“a”,“b”所示原子和“L1”所示格点位置关系,“L1”即LSIA. (3)若没有任何原子“归属”某个格点,则该格点位置被判定为空位. 如图中“L2”所示格点位置.

3 模拟结果

图2为通过可视化软件观察到的PKA能量为10 keV时级联碰撞的一个例子.

图2a为级联碰撞的初始阶段,只有少量原子被碰撞出来,形成离位原子;图2b为随着级联碰撞发展,更多原子成为离位原子,并逐步达到离位峰阶段;图2c表示部分间隙原子重新被空位捕获,晶体缺陷数减少阶段;图2d表示模拟系统恢复稳定,缺陷进入由温度驱动的自由演化阶段. 整个模拟过程中点缺陷数的变化呈现迅速升高到峰值、逐步减少、基本稳定等三个过程,这与通常对级联碰撞过程的认识一致.

上述过程还可以通过模拟系统温度场的变化得到印证. 本研究截取了级联碰撞最活跃的区域,通过不同颜色标记每一个原子的动能范围,绘制了该区域温度场的变化情况,如图3所示.

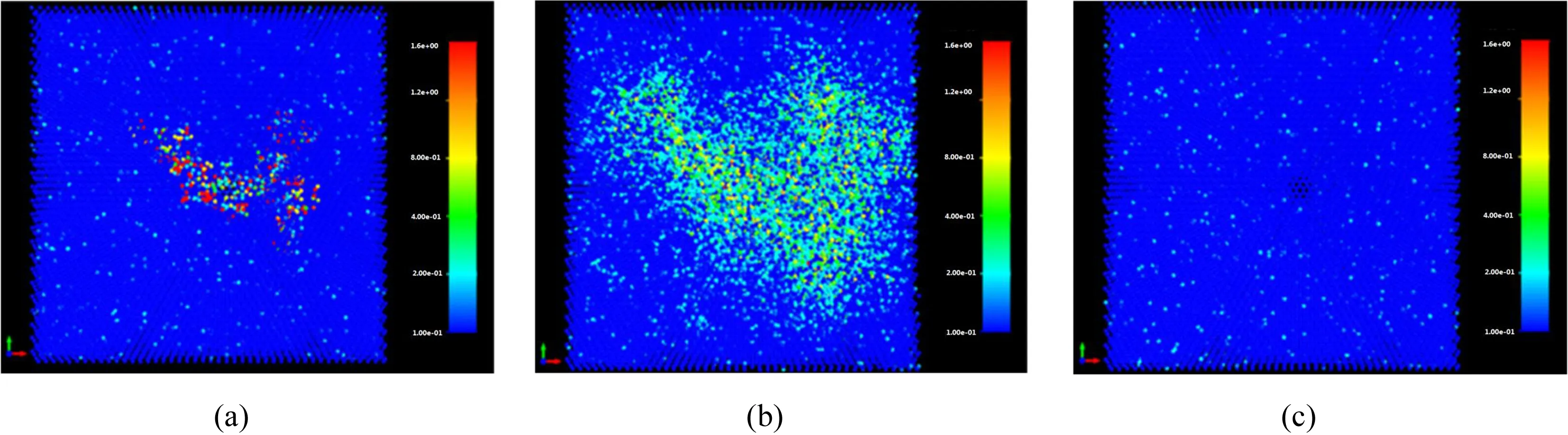
图3 温度场(a=0.1 ps; b=1 ps; c=10 ps)Fig.3 Temperature field (a=0.1 ps; b=1 ps; c=10 ps)

图3中,高能原子用红色表示,低能原子用蓝色表示. 级联碰撞之初,存在大量高能原子,这些原子和周围原子发生碰撞时,新原子获得的能量易超过离位阈能,从而被激发出来形成离位原子并使得级联碰撞可以持续下去(如图3a所示);离位峰出现后,大部分原子的能量已经降低,不足以激发出更多离位原子原子(如图3b所示);模拟系统恢复平衡后,原子基本恢复到模拟盒子本底温度,只在热驱动下演化(如图3c所示).

本文采用2.2节中介绍的3种方法分别对MD模拟结果进行了点缺陷判定. 以PKA能量10 keV为例,点缺陷的变化趋势对比如图4所示.

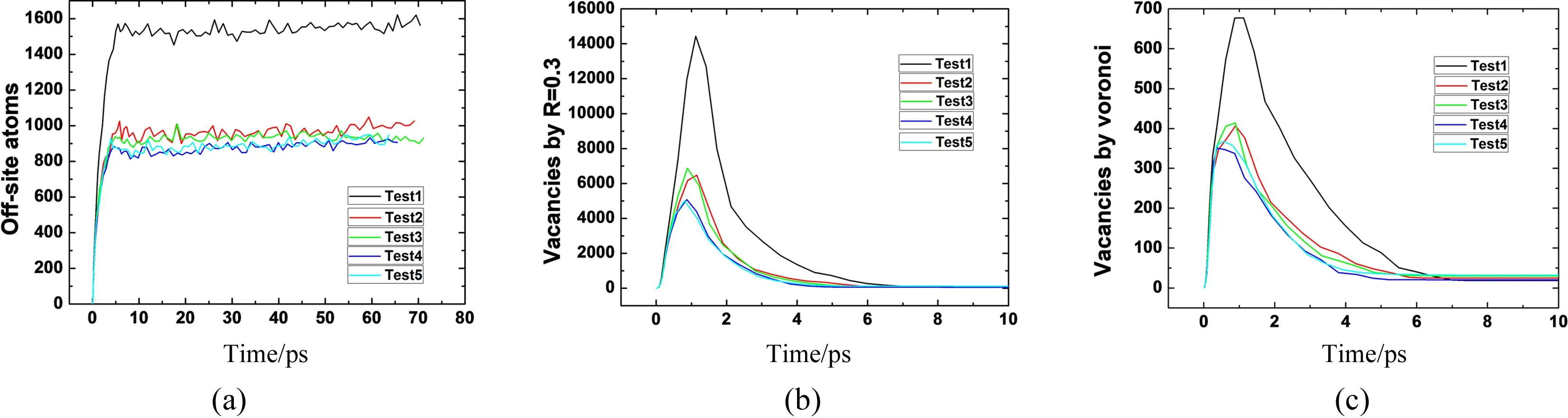
图4 点缺陷演化比较(a:方法1; b:方法2; c:方法3)Fig.4 Point defects evolution comparison(a: method 1; b: mehod 2; c: method 3)

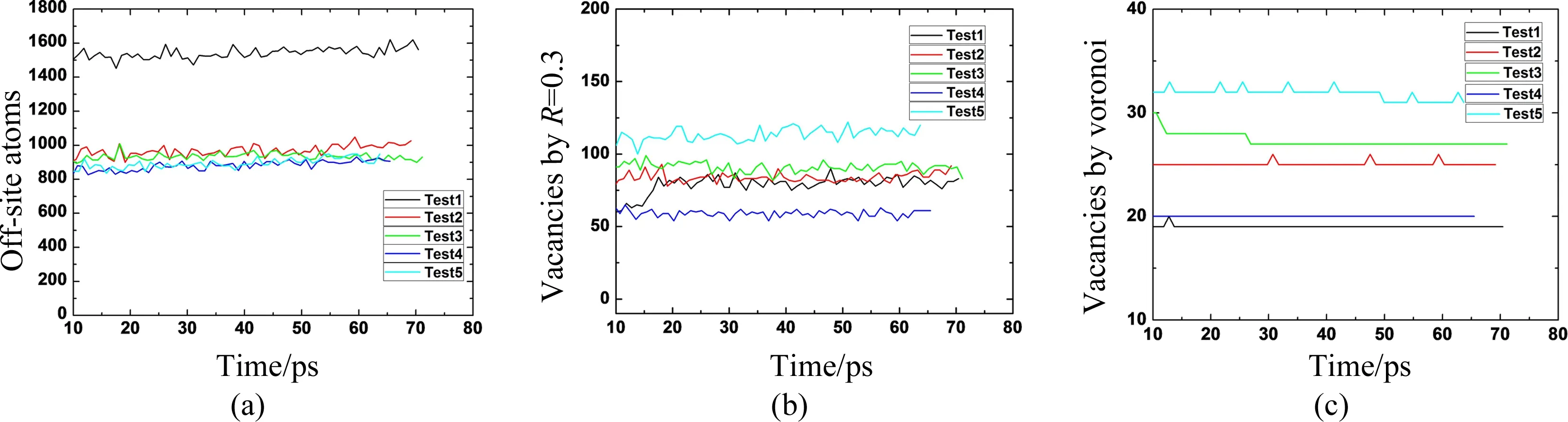
图5 统计涨落及鲁棒性比较(a:方法1; b:方法2; c:方法3)Fig.5 Fluctuation and robustness comparison (a: method 1; b: mehod 2; c: method 3)

由图可见,离位原子数变化呈上升趋势,尽管模拟系统恢复稳定后变化趋缓,但总体未出现减少过程,这表明方法一不能体现间隙原子被空位重新捕获的情况. 方法二和方法三中,尽管峰值以及稳定后的缺陷数不同,但变化趋势总体一致,和图2结论自洽,可以完整反映级联碰撞各个阶段缺陷数的变化情况.

模拟系统恢复稳定后,缺陷在温度驱动下自由演化,此时的缺陷数可以用于反映晶体的损伤程度. 此阶段3种判定方法获得的陷数统计涨落以及判定方法鲁棒性的对比如图5所示.

由图5可见, 5次分子动力学模拟获得的离位原子数统计涨落最大,在约800～1 600;方法二获得的点缺陷数统计涨落也较大,在约60～120之间;W-S分割方法获得的点缺陷数统计涨落最小,在19～33之间. 统计涨落越小,意味着获得较准确平均值所需的模拟次数越少,可以相应节约计算开销.

判定方法的鲁棒性比较方面,方法一和方法二获得的缺陷数都因缺陷在温度驱动下的自由演化而出现明显振荡,而W-S分割方法获得的缺陷数非常稳定,很少出现变化,表现出良好的鲁棒性. 鲁棒性越好,意味着单次模拟所需的时间越短,同样可以节约计算开销.

方法一和方法二中需要设置判定阈值,本文还研究了阈值对分析结果的影响. 以方法二为例,图6显示了R=0.3a0、R=0.35a0和R=0.4a0时获得的点缺陷数.

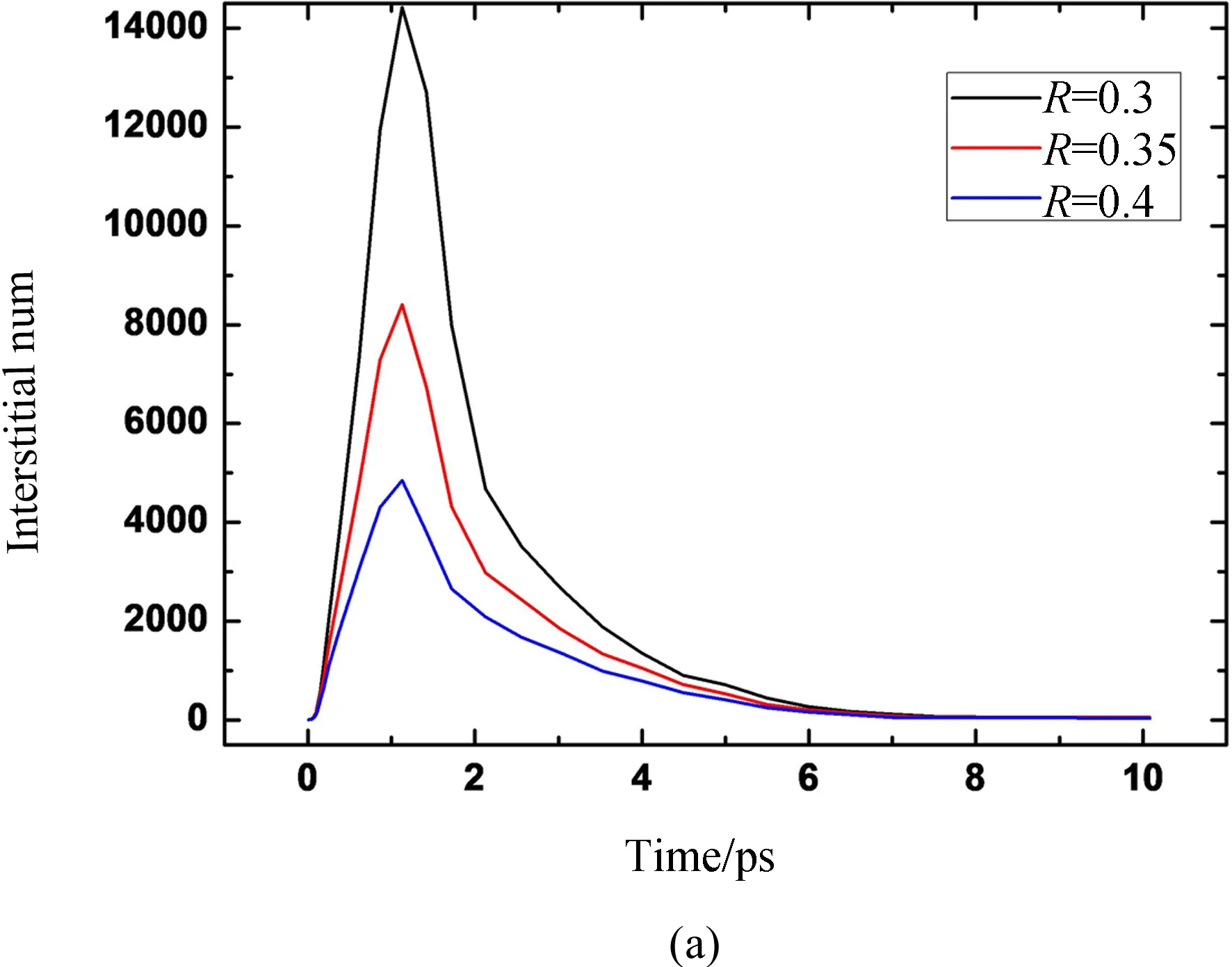
图6 阈值R影响

图6a为10 ps以前模拟结果,图6b为10 ps以后模拟结果. 整个过程中,采用不同R值进行判定获得的点缺陷数差距很大. 这表明以距离阈值为判定依据的缺陷数分析方法对阈值的设定非常敏感.

综上所述,方法一单纯计算原子和初始位置的距离,未考虑原子和其它格点位置的关系,因此无法识别间隙原子被其它空位再捕获的情况;方法二本质是一种范围判定,它可以识别间隙原子被其它空位再捕获的情况,但是如果由于R设置的敏感性造成部分间隙原子可能落在R范围内,这些间隙原子将被识别为普通原子,从而造成间隙原子和空位数不匹配;方法三采用了相对距离判定,无需设置阈值参数,而且可以保证间隙原子和空位数一定相等. 因此,从3种判定方法获得的晶体缺陷数变化趋势、统计涨落;方法的鲁棒性、对阈值的敏感性等多方面评价,采用W-S原胞分割判定方法获得的点缺陷数更适合准确反映晶体受到辐射后的损伤程度.

本文还对10、20、30、40和50 keV PKA能量的分子动力学模拟结果进行了分析. 采用W-S方法获得的点缺陷数变化如图7所示.

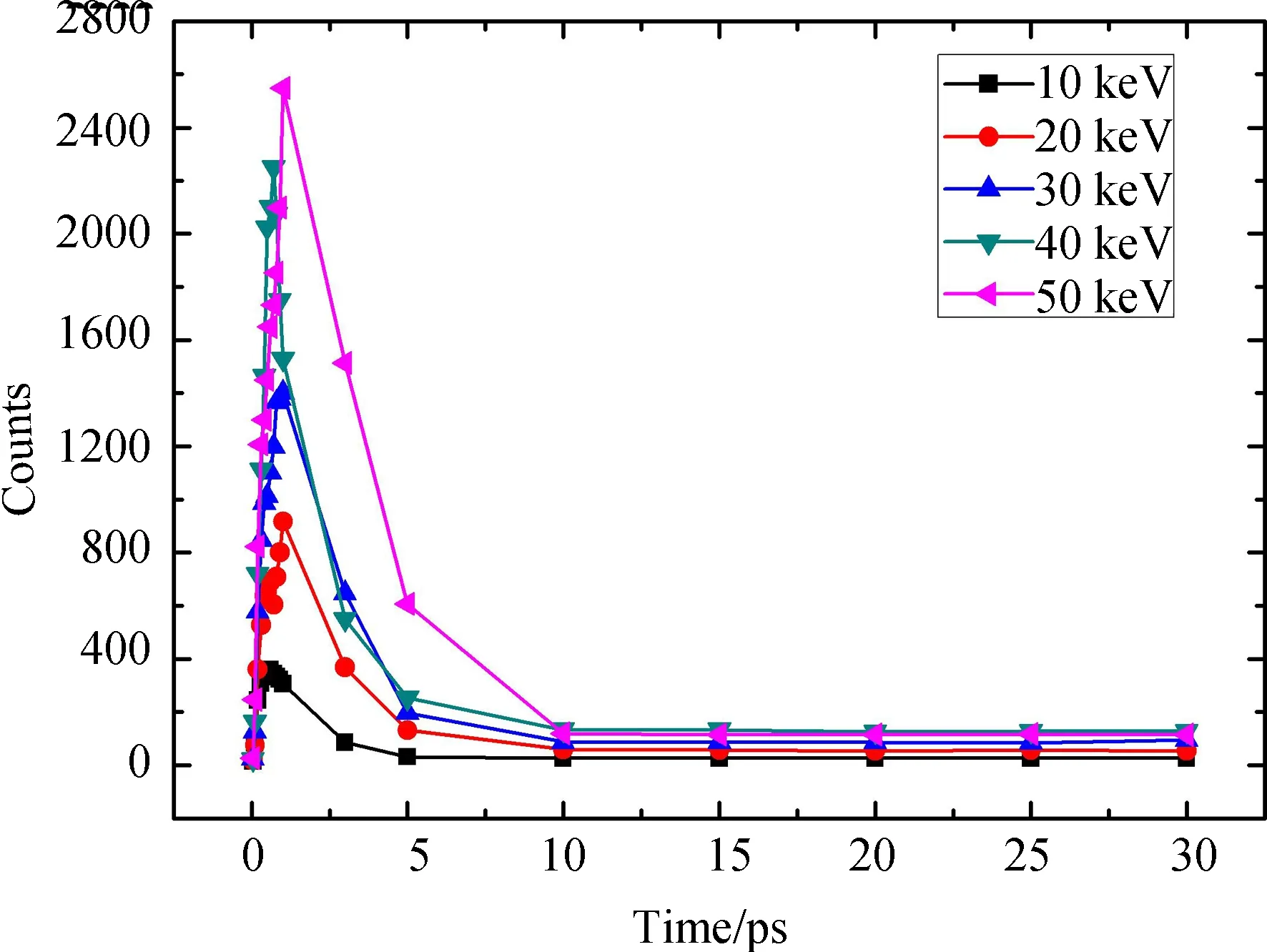
图7 不同PKA能量产生的缺陷数Fig.7 Defects number in different PKA energies

不同PKA能量条件下缺陷数演化过程一致. 缺陷数和PKA能量基本成正比,缺陷数峰值出现在1 ps附近,模拟体系恢复平衡在10 ps附近,以上两个时刻基本不随PKA能量改变而发生变化.

图8 300 K时LSIA扩散轨迹Fig.8 Typical trajectories of LSIAs for temperature T=300 K

表1 ILJ,OLJ,OPJ比例

由表可见,OLJ类跳跃是主要的跳跃方式. 因此LSIA更倾向于2D扩散.

4 结 论

本文采用分子动力学方法模拟了5种PKA能量引起的Zr原子的级联碰撞,同时采用了3种不同的点缺陷判定方法对MD模拟结果进行了分析. 其中,W-S原胞分割方法具有良好的鲁棒性,不需要设置任何阈值参数,多次模拟所获的点缺陷数的统计涨落很小,更适合表征晶体的辐射损伤程度. 此外,分子动力学模拟结果表明,Zr级联碰撞后的点缺陷数正比于PKA能量,离位峰出现在级联碰撞开始后约1 ps左右,系统恢复稳定出现在约10 ps左右. 以上两个时刻基本不随PKA能量变化而发生改变. 此外,SIA的扩散更倾向于是一种2D扩散.

事实上,正如我们熟知的,中子辐射损伤基本可以分为两个阶段,第一个阶段是由原子级联碰撞造成初级辐射损伤,这个阶段发生在皮秒(ps)量级. 本文主要针对这一阶段的物理过程以及点缺陷的判定方法进行研究. 第二个阶段是由初级辐射损伤造成的缺陷在温度驱动下的演化过程,包含缺陷的扩散、团簇的捕获与解离等过程. 第二个阶段的时间尺度远远大于第一个阶段,可以采用分子动力学、KMC或者速率理论等方法进行. 需要指出的是,对第二阶段模拟需要缺陷的初始状态,包括点缺陷数和分布等,则依赖于由第一个阶段的模拟结果提供. 因此,本文关注缺陷判定方法的鲁棒性等的目的都在于确保第一阶段获得的参数更为准确,对下一步多尺度模拟的参数选择具有一定的借鉴意义.