基于mRMR与因子分解机的分类模型研究

王 美， 龙 华， 邵玉斌， 杜庆治

(昆明理工大学信息工程与自动化学院， 昆明 650000)

1 引 言

对恐怖事件聚集性的研究，前期对其研究多是使用对数据汇总统计的方法来显示事件中特定变量随时间变化的趋势.1999年Enders等人使用时间序列模型，分析恐怖事件对国内生产总值GDP的影响，得出当恐怖事件减少时GDP呈现增长的结论[1].2002年Major使用博弈论与概率分布量化风险，对恐怖事件具体因素隐藏的信息进行分析[2].2003年Sandler使用博弈论理性分析了恐怖组织与目标国家间的相互作用，得出一个国家的游客、公民和企业，由于他们威慑能力小，较容易成为攻击目标的结论[3].Guo等人在文中分析上述章节所建立的统计与数学模型是基于先验假设和完备的数据集，然而当下因各种原因，GTD数据集所记录的数据往往不完整或是存在不确定值，所以使得制定有效假设和检验假设能力受限[4].故需探索新的可视化和计算方法，以得到分析GTD数据更好的模型.

在探索新的分析方法中，首先是Wang等人采用协调多视图的方法开发了用于探索恐怖事件数据的可视化分析系统，可揭示一些未知的恐怖袭击事件发生趋势和规律，但该方法中多是对数据汇总统计结果进行可视化，没有对GTD数据本身存在的稀疏性以及高维度多冗余问题进行很好的处理[5].Pagán发现了该问题，开始引入了数据清洗策略，Pagán在文中采用均值替换法MI、中值替换法MDI以及K近邻填补法KNNI对GTD中的缺失数据进行填充[6]，清洗后的数据用于线性判别分析LDA、K最近邻KNN以及分类决策树RPART分类器GTD中对伊拉克组织的恐怖袭击事件进行分析.由于GTD中存在大量缺失值和冗余特征，全部采用填充方式使得数据集产生了不可忽略的偏差等原因，最终分类效果并不是很理想，交叉验证错误率均在40%左右.为了减小GTD中的冗余特征量以及合理处理缺失数据，Iqbal等人[7]对数据进行了降维，并对缺失值增加了删除处理方式，不足的是文中基于主观对问题的理解，对特征采用了手动选择特征方式降维，使得分类结果有很强的主观色彩.在后面的研究中，处理对GTD数据的分类多是采用机器学习方法，2016年Muhammad 等人使用监督学习方法如贝叶斯分类器和决策树分类器，对特定巴基斯坦的GTD集进行分析[8]；2017年Dong使用BP神经网络对印度恐怖袭击事件进行了分析预测[9]；Ding等人采用经多途径选择的十二个特征，使用神经网络，支持向量机(Support Vector Machine,SVM)和随机森林(RF)宏观预测分析2015可能发生恐怖事件的地方[10].但就恐怖袭击事件数据本身而言，前面实验中都未有很好的考虑数据集高维度稀疏性大的问题，如高维度稀疏数据会使得BP预测效果很差等，针对解决手动特征降维问题，Mo等人采用了最大相关性(Max-Relevance)以及最大相关性最小冗余mRMR特征选择方法获取特征集[11]，并结合支持向量机(SVM)，朴素贝叶斯(Naive Bayes,NB)和Logistic回归(LR)分类器对恐怖袭击事件进行分类研究，文中有效地验证了将机器学习应用于恐怖主义研究领域的可行性，但文中训练集是采用专家定义对事件进行分类，且未解决选取后的优化特征集仍存在的数据稀疏性的问题，这将会影响分类效果不佳.

基于以上问题，同时与文献[12]提出的混合变量选择算法相比，因FM往往有很好的通用性能，且常能取得较好的效果且善于处理稀疏数据集的特性[13]，故本文提出一种基于“最小冗余最大相关”(Minimal-redundancy maximal-relevancy，mRMR)与“因子分解机”( Factorization Machines， FM )结合的TFM分类模型，mRMR使用增量搜索方法寻找近似最优的特征集，找到最佳特征子集以最大化分类精度，并结合因子分解机FM模型对GTD进行量化分类.

2.1 数据预处理

公开数据集“全球恐怖主义研究数据库”(Global Terrorism Research Database,GTD)[14]具有高维海量数据，大数据的低价值的特征，存在大量未记录缺失数据，为了提高数据的质量，所以需要进行数据预处理.

文中用二分类法对GTD展开讨论，假设GTD数据集表示为

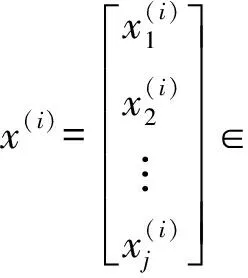
Rj,i∈(1,m),j∈(1,n)

其中，m表示总的事件数；n表示GTD数据集总的维度.

定义1定义GTD事件类型为y(i)={0,1}，若此处以1表示A组织所为事件，则0与之相反，则测试集表示为(x(1),y(1)),…,(x(i),y(i)),i∈(1,m)，m表示总的事件数，因GTD 数据具有高损失率的问题，采用数据剔除法进行预处理.

定义2定义特征j的缺失率为

(1)

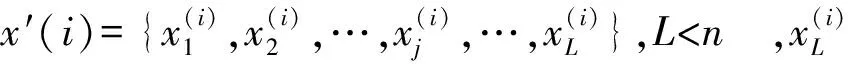
2.2 mRMR特征选择

mRMR算法[15]是根据特征与目标分量间相关性以及特征与特征间的冗余性进行特征提取，其中,相关性和冗余性用互信息量(MI)值大小表示；MI与相关性成正比，互信息的定义如下.

(2)

O=MI(xf;c)，f≤n

(3)

Gt中的特征向量xt与Gs中的全部特征向量间的冗余R度计算如下式.

(4)

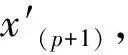
(5)

当总的特征为N(=s+t)时，mRMR的特征评估将进行N轮.经过mRMR评估后原特征集{x1,x2,…,xN}，重新排序后的特征集表示为s如下.

最终最优特征集取目标函数最小损失值对应的s中的H(≤N)个特征.

2.3 TFM分类算法

TFM算法意在构建分类模型，结合了因子分解机算法FM[16]和分类阈值算法.

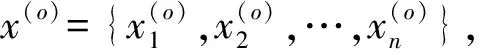
(6)

式(6) 计算复杂度为O(kn2)，根据文献[16]将式(6)计算复杂度化简为O(kn)后，表达式如下式.

(7)

假设FM中所有参数Θ={w0,w1,…,wn,v11,…,vkn}，为了避免产生过拟合现象，所以此处FM最优化目标选取正则化的最小二乘法.

(8)

其中，x(i)表示第i个事件；loss( )为损失函数；λθ表示参数θ的正则化系数.结合以上分析，模型中参数{w0,W,V} 可采用随机梯度下降法SGD对进行学习，计算伪代码可见ALGORITHM 1.

分类阈值算法，加入该算法以实现二分类，假设训练集中属于A分类的有z件，于A分类的有a件，则取阈值函数：

(9)

当事件x(i)预测值P>P′时，预测结果属于A分类，反之不属于.

TFM模型是将FM计算得到的预测结果，与分类阈值结果比较然后归类得到分类结果.

2.4 模型评估

2.4.1 logit loss损失函数 logit loss 是普遍认可的一种模型分类效果分类标准[17]，其定义如下.

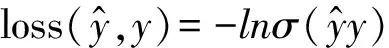
(10)

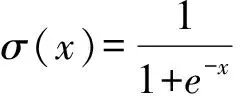
2.4.2 分类指标 分类模型性能评价指标中常使用的有准确率、召回率和灵敏度[18]，以及本文采用的马修斯相关系数(Matthews Correlation Coefficient,MCC)[19]衡量指标 :

(4) 马修斯相关系数:MCC=

上式中的TN、FN、TP以及FP定义如表1所示.

表1 分类评价指标定义

TN为被模型预测为负的负样本；FN为被模型预测为负的正样本；TP为被模型预测为正的正样本；FP为被模型预测为正的负样本.

文中使用了不同的模型进行分类效果比较，鉴于MCC同时考虑了TP、TN、FP和FN，可用来很好的衡量分类效果，MCC越大越好，故本文选用MCC评价指标.

实验中，我们采用了全球恐怖主义研究数据库GTD数据集. GTD记录了从1970年至今世界各地的恐怖事件信息，并且不断的更新各种恐怖事件，至今已超过14万恐怖袭击事件，且每一个事件超过45个特征记录值，这使其成为目前是介绍基于恐怖事件的最全面的非机密数据.文章中选取了2001年至2017年近17年南亚地区A组织所为事件分别打标签得到分析数据集G.表2列出分析对象近17年的18 737个总事件，其中分别对A组织所为和非其所为事件数进行统计，并打标签，A组织所为标记1，反之标记0.

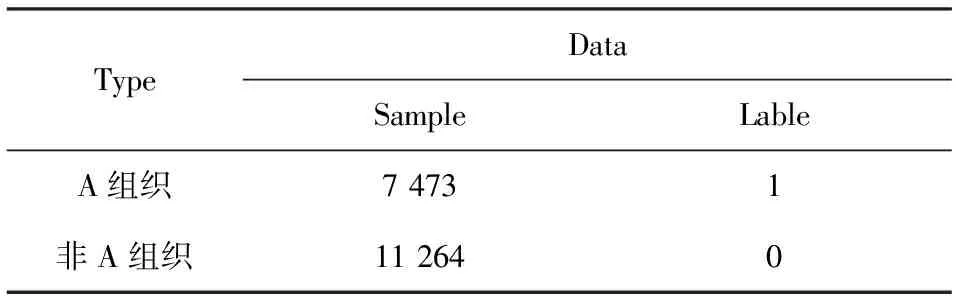
表2 恐怖事件组织和标签

我们将按照2.1方法对数据集G进行处理，处理后的数据集G中pj>0有一半特征，说明处理后的GTD数据集中仍存在大量未记录数据或空值数据.

我们于Python 3.6上完成实验，实验中首先使用mRMR函数应用于A组织训练集，根据式(5)增量特征选择方法获取诸多特征子集，实验有58个特征故共有58个候选子集.我们对训练集使用四折交叉检验获取训练集和验证集，图1所示为每一个候选子集对应的FM预测输出与分类结果的损失值，我们从图中观察与后台计算结果对应取最小损失值6.044 257 3对应的36个特征子集为最优特征集.

图1 mRMR选取特征子集对应的分类损失值Fig.1 Loss value for feature subset based on mRMR

许多方法都用于分类模型中,如文中提到的逻辑回归(Logistic Regression,LR)、支持向量机SVM和朴素贝叶斯，但是很难说明哪种分类比较好，不同的数据集适合不同的分类模型.本文基于mRMR确定的最优特征集应用GTD数据集对TFM、LR、SVM和NB其分类进行了实验，实验中采用了tensorflow框架实现TFM模型，极大化的优化了模型的实现，分类具体效果比较见表3.表3中耗时为测试时长T，即测试所用时间.由表3可直观看出TFM分类准确率与MCC值均优于三个模型，LR次之，NB准确率和MCC最为不理想，但就耗时来说TFM相对微大于三个模型，就此问题来分析，分类结果供人为使用分析，故毫秒的差异不足以影响使用效果.结合结果与LR[20]、SVM[21]以及NB[22]模型特点可分析，TFM将特征映射到高维来考虑特征与特征间的关系，且TFM通过引入辅助向量迭代求取两个特征间的参数，故效果较好，但也正是引入了辅助向量，故相对于其他三个模型来说耗时略大些.

从表3可知，TFM分类效果较稳定，准确率也较高.表4所示事件即为TFM分类正确，但其他三个模型失效的案例.C1是2006年11月19日的一个暴恐事件，属于A组织所为，正确归类应是1；C2是2008年7月7日的一个暴恐事件,非A组织所为，正确归类应是0.TFM的分类错误率1.7%低于LR的2.95%、SVM的3.03%以及NB的26.56%，所以在GTD分类模型中可优先考虑TFM模型.

表3 TFM与其他模型比较

表4 事件C分类结果

从实验可知，TFM模型有一定优势，但存在耗时T略大问题，分析是因为TFM模型中引入辅助向量导致.在以下场景中该问题可做如下优化：(1) 如类似本文分类结果供人为使用分析的分类中，毫秒的差异不足以影响使用效果可接受；(2) 选择适合的数据集，因为该模型原本就为解决稀疏数据分类问题而提出，故合适的数据集，即使耗时稍大，但效果明显，如此处采用一个稀疏度约为0.029 6的0和1组成的数据集(此处定义：稀疏度=非零总数值个数 / 总数值个数)做个测试实验，结果如表5所示，值得分析的是从表5中看LR与SVM准确率相同，侧面反映出SVM将特征映射到高维部分计算失效，只有线性部分有用，正如文献[16]说的处理稀疏数据时FM比SVM更有优势，当数据过于稀疏时SVM失效，所以最终结果与LR一致，同时说明在处理稀疏数据集时FM有利于高维部分的计算；(3) 类似医学中癌症症状分类，或关键时刻的模糊稿件字符识别分类如罪犯笔迹等中，记录数据较为稀疏且更为要求分类性能稳定，效果较好的情况，可以一定的时间为代价，得到更准确的分类效果，此时可考虑TFM分类模型.

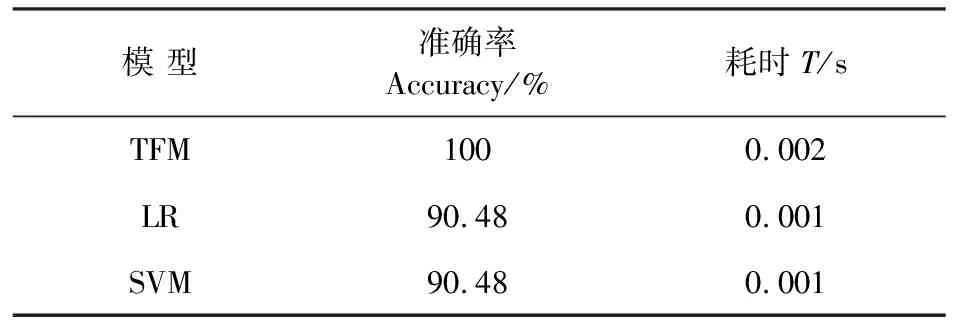
表5 运用TFM模型稀疏测试数据结果

5 结 论

由以上分析可知，类似于TFM和LR类的机器学习方法可用于分析恐怖主义数据的特征关系，且具有高准确性和快速性.本文基于GTD数据集，使用Python3.6统计数据，使用mRMR算法获取分类损失函数值最小的优选特征子集，对准备好的数据集使用不同的分类器进行分析.我们得出结论：TFM优于其他三个模型，但其代价是耗时略多，但也有一定的优化方案在第四部分中进行了概括.所以总体来说分类GTD时，若需要更为准确的分类效果则选TFM，若更为追求时间成本，则可选用LR或SVM算法.当然在实验中遇到特别稀疏的数据集，TFM模型较合适.总的来说考虑了mRMR特征提取算法，结合了FM模型与分类阈值算法的TFM模型确实量化了对恐怖事件的分类问题，之后可在此基础上进行更多的研究.如文献[23]中提出的改进mRMR特征选择方法，融合多种相关度量方式对特征子集进行特征选择，可以恐怖主义事件为数据集展开优化mRMR算法问题以及考虑多分类问题等.