基于隐式马尔科夫模型的舰队应召搜潜方法
卞大鹏,余珊珊,张诗,余明晖,王云
1 海军装备部驻武汉地区第二军事代表室,湖北武汉430064
2 华中科技大学自动化学院,湖北武汉430074
3 中国舰船研究设计中心,湖北武汉430064
0 引 言
反潜作战是水面舰艇主要作战任务之一,而对潜搜索(以下简称“搜潜”)是反潜作战的重要组成部分[1],也是水面舰艇对潜跟踪、防御和打击的前提。
目前,国内有学者将水面舰艇编队搜潜与路径规划问题相结合,来研究搜潜过程中的最优路径。赵亮等[2-3]针对多舰协同应召搜索水下运动目标的路径规划问题进行了研究,建立了多个搜索者搜索路径的规划模型,并设计了一种多种群协同进化自适应进化算法,得到了协同搜索的最优路径。沈治河等[4]对水面舰艇搜潜进行了仿真分析,研究了舰艇编队的优化配置和兵力机动方法,对于提高水面舰艇编队搜潜效率有着重要的意义。国外学者从搜索理论[5]出发研究了各种搜索优化模型。Martins[6]开发了一种分支定界算法,即通过最大化预期的探测数量来计算搜索路径解决方案的上限。Kierstead 等[7]研究了将遗传算法应用到复杂环境中,对移动目标进行路径规划的问题。上述文献都是将研究的区域作为整体,当改变区域中一个障碍物位置时,必须重复所有的仿真操作,从而增加了仿真的复杂性。
本文拟采用区域划分的方法,仿真时改变某块区域的条件,只要保证该区域最优路径的首尾位置不变,就可以只对该区域进行仿真。
应召搜潜是指我方已知敌方潜艇最后时刻出现的位置,在此基础上对该位置附近的海域进行搜索。本文拟利用隐式马尔科夫模型(HMM)对敌方潜艇运动建模,分配搜索者和搜索区域,规划搜索者的路径,使用进化算法(EA)找到最优搜索路径。
1 应召搜潜潜艇运动模型
水面舰艇编队应召搜潜时,潜艇运动轨迹是隐藏的,但其状态可由反潜系统的观测来推断。本文采用HMM 模型对其进行建模分析,过程如图1 所示。搜潜马尔科夫链符号说明如表1 所示。

图1 搜潜马尔科夫链Fig.1 Markov chain of searching submarine

表1 搜潜马尔可夫链符号说明Table 1 Symbols used in markov chain of searching submarine
1.1 模型假设
马尔科夫模型的2 个基本假设:
1)在任意时刻的状态只依赖于其前一时刻的状态,与其他时刻的状态和观测无关[8]。
2)任意时刻的观测只依赖于该时刻的状态,与其他时刻的观测和状态无关。
1.2 模型建立

在HMM 模型中,利用概率来表示状态和观测时间序列的随机性,而状态时间序列是不可见的,故初始状态概率分布、状态转移矩阵和观测概率都直接给出,最后由状态得到观测时间序列。
建立的HMM 模型中包含有以下参数:概率转移矩阵Γ、观测概率矩阵B、目标初始概率φ等。这些参数在初始化时可假定为已知,直接进行计算。
k=0 时,目 标 初 始 概 率 分 布-π( )0|0 为φ,由下式表示示为

式中:p为区分搜索标号;j 为搜索区域单元格标号。
概率转移矩阵Γ为

式中:γgj为目标从单元格g 转移到单元格j 的概率;j∈Cg,表示目标只能从上一时刻的位置x(k-1) =g移动到其相邻的单元格。而是否探测到目标与隐式马尔科夫的观测概率矩阵相关。
观测概率矩阵B表示为


式中:ui(k)=j,为在k时刻搜索者i 正在搜索单元格j∈Ai;oi(k)∈{0 ,1} ,为搜索者i 在时刻k的探测结果(探测到目标为1,未探测到目标为0)。

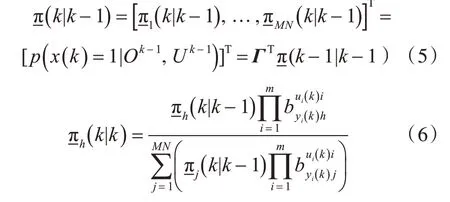

2 基于EA 算法的搜潜路径优化
2.1 目标函数
当路径规划周期为给定值时,将目标函数最大化,从而得到全部m 个搜索者的搜索区域分配情况,以及每个搜索者i 的搜索路径,如式(8)和式(9)所示。

2.2 分配限制
对于m 个搜索者,将全部搜潜海域划分为m块搜潜区域,在k时刻,搜索者i被划分到Ai(k)(i=1,2,…,m)区域,该过程为随机分配,只需保证每个区域有且仅有一个搜索者,以及所有区域加起来为整个搜潜海域的面积且区域之间未发生重叠。此外,还需要保证每个搜索者在每个时间周期内划分的区域是连续的。具体限制条件如下:

式(10)表示所有搜潜区域的总和为整个搜潜海域的面积;式(11)表示各搜潜区域之间无重叠,式(12)表示在k-1 时刻搜索者i 所在位置ui(k-1)的相邻单元格Cui(k-1),其部分或全部属于搜索者i在k时刻所在的搜潜区域A(ik)。
2.3 网络流限制
网络流约束确保了在第1 次搜索开始时,每个搜索者的启动单元都使用约束式(13)初始化,即搜潜者i 第1 次的搜潜位置必须在被分配的搜潜区域Ai( )1 之内。
在最后一个搜潜时刻,所有的搜索者都到达终止单元格,且此单元格在对应的搜潜区域之内,该约束由式(15)表示。式(14)所示的约束保证了搜索者下一次只能移动到分配区域内上一次所处位置的相邻单元格之内。


3 两阶段启发式求解方法
由于搜索者分配和搜潜路径规划是NP-hard问题,在复杂约束条件下,若在庞大的搜索空间中寻求最优解,传统的搜索方法几乎不可能做到[9]。因此,在准备阶段和路径规划阶段都采用启发式求解方法来解决此问题。准备阶段是在搜潜周期开始时将搜潜海域划分成小的区域。为保证m 个搜索者搜索路径的限制,需要把搜潜区域划分成空间相邻的m 个不重叠区域,且为每个区域分配1 个搜索者。路径规划阶段是在所有的搜潜周期内为每一个搜索者在其搜潜区域内规划一条搜潜路径。
3.1 准备阶段
此阶段包括搜潜区域划分及搜索者的分配。
首先,将搜潜海域A 划分为互不重叠的m 个搜潜区域An(k)。在自然社会中,通常某个对象受其近邻的影响是不同的,通常是距离越近的对象对其影响越大,故在本文中采用距离最近邻算法[10],最近邻算法需要在整个搜潜海域内先选取m 个质心。然后,计算剩余的单元格到质心的欧氏距离,并将单元格归并到最近的质心所在类。每个质心对应于EA 算法中的1 个基因,m 个质心,其中对应m 个个体。最后,在每个搜索周期初始阶段进行规划,每个个体的搜索区域通过计算与搜潜中心单元格j之间的距离来生成。
在k∈{1 ,T+1,2T+1,…,K-T+1} 时刻,首先得到划分好的搜潜区域An(k),然后对搜索者进行分配,即将m 个搜索者分配到m 个搜索区域中。搜索者分配问题描述为

约束条件为
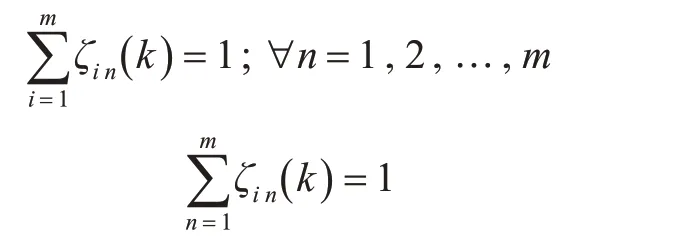
其中,
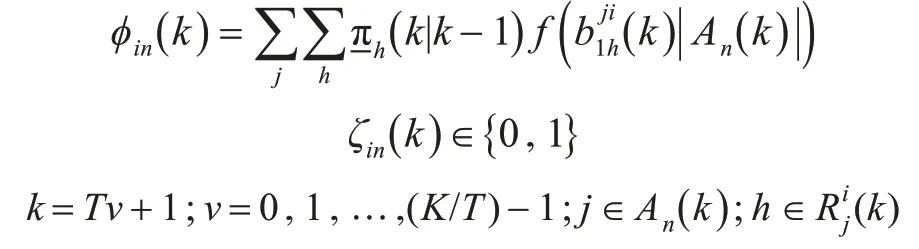
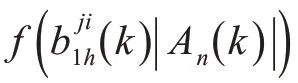
通常该函数可以写为

式中:Φ为累积正态分布;σ(|Ai|)为线性组合后的缩放比例因子,即文中仿真使用的参数。其中b 和β是缩放比例因子,一般β为2 m,b 的值是为了保证累积正态分布的方差在合适的范围内,按照本文仿真中的取值即可。
为了在特定k时刻将m 个搜索者在m 个搜潜区域内进行分配,首先令搜索者和搜潜区域两两组合,通过式(16)的目标函数计算得到m×m的增益矩阵,然后找到一个最优的分配方案。上述双向分配问题可以用排列组合和EA 算法相结合来解决,式(16)的目标函数即为分配方案对应的适应度值。
本文采用十进制EA 算法的编码方式,染色体长度为质心数量m。在选取质心时,要求m 个质心在空间上不相邻,以避免在区域划分时出现极端搜潜区域过大的情况,并且可加速整个算法找到最优个体,避免产生适应度极差的个体。
本 文 选 取Order-Based Crossover(OBX)[11]交叉方式来对染色体进行交叉操作。首先,随机选择1 对染色体(父代)中的1 个基因,这些基因在双亲中的位置相同但可以不连续。在选取的基因中要保证在对方的染色体中基因不相同,以避免交叉操作后出现1 个染色体有2 个相同的基因的情况,即指选取的质心重叠。然后,对这些基因进行交叉替换操作。突变选取常用的单点突变,随机选取要突变的基因位点,并突变为与剩余的其他基因不同的基因。图2 所示为EA 算法的流程。

图2 EA 算法流程图Fig.2 Flow chart of evolutionary algorithms
当排列组合与EA 算法相结合时,每个个体的适应度值对应的是与搜索者分配到搜索区域的分配问题相关的目标函数值。在下次迭代中,新的个体基于现在个体的适应度值生成,重复此过程直到分配解决方案收敛。预测目标概率(k|k-1) 在搜索者分配时是不更新的,并且只有在第1 次将搜索者分配到搜潜区域时才需要对搜索者进行排列组合分配。对于搜索者的重新分配只使用最近邻算法,它基于搜索者当前的位置,并确保每个搜索者只能被分配到1 个区域来生成划分范围。这个过程确保了每个搜索者的搜索路径约束。在实验中,不考虑不可穿越的单元或障碍。
3.2 路径规划阶段
在此阶段,有些路径规划的限制需要明确表述。例如:搜索者从当前单元格开始搜潜,下一步只能搜索与当前单元格邻近的8 个单元格中的一个。在每个时刻,该问题可以表示为

约束条件为:

其中,

目标函数可以用来计算新个体的适应度值,它表示要在本搜索周期内找到一条使搜潜体目标命中期望值(ED)最大的路径。预测的目标分布概 率(k|k-1) 可以在各时刻根据种群中最优个体的搜索序列进行更新。为了确保搜索者的移动被限制在邻近单元格之内,目标函数要遵守网络流限制和邻近限制。在上述约束条件中,式(19)表示在本搜索周期开始时搜索者都在自己划分的搜潜区域内;式(20)表示本周期第1 个搜索位置与上一个周期最后一个搜索位置是相邻的,这保证了在2 个周期之间搜索路径是相连的;式(21)表示在本周期之内同一个搜索者在任意相邻时刻的搜索位置在空间上是相邻的,保证了搜索路径是连续性的;式(22)表示在下一个周期开始时搜索者都在自己划分的搜潜区域内。
最优搜索路径的问题可以由EA 算法来求解,每个个体代表了整个搜索时间内所有搜索者的一种可能的搜索路径。种群大小和具体搜潜海域相关,种群的下一次迭代可以通过交叉和变异操作来完成。若被选中的双亲进行交叉操作而且二者含有相同的基因,则其后代可以通过交换基因片段来完成。
1)编码。如图3 所示,Pi为第i 个搜索者(i=1,2,…,M);Tk为第k个时刻(k=1,2,3…,N);xik为搜索者i 在k时刻的位置。因为搜索者的速度限制了其只能在下个时刻移动到与其邻近的单元格位置,所有同一个搜索者内基因体之间是有联系的,每个基因都取决于其前一个基因,第1 个基因的位置与最初的分配位置有关,而且每个搜索者的位置还要限制在其搜潜区域内。即

式中,Ri(k)为搜索者i 在k+1 时刻能够移动到的区域。

图3 染色体编码示意图Fig.3 Chromosome coding
2)交叉操作。本文中,交叉操作时需要双亲对应的搜索者在某一基因位点有相同值,即都搜索过此单元格区域,这是对其进行交叉操作的前提。每个搜索者在进行交叉操作后需要保证长度不变,如此才能保证交叉操作后子代的染色体的长度与双亲是一样的。但往往双亲是在不同时刻对同一单元格进行搜潜,故交叉操作后搜潜路径会有加长和缩短的现象,为保证染色体长度不变,需对染色体进行剩余切割操作和不足增添操作,单个搜索者搜索步长为8 单元的染色体交叉如图4 所示。

图4 染色体交叉过程图Fig.4 The process of chromosome crossover
图4 中:黄色表示某搜索者的初始位置,第1个基因需要根据此位置生成;红色表示2 个搜索者都对此位置进行了搜索,所以可以对染色体进行交叉操作。由于交叉点在双亲中的位置不同,为了保证交叉操作后染色体长度不变,需要在此操作后的染色体末端进行基因删除以及基因随机生成的操作。鉴于一条染色体对应了多个搜索者,所以一条染色体最多可以进行m 次交叉操作。
3)变异操作。对选中的基因进行操作,根据该基因的前、后基因,决定是否对其删除或者进行上、下、左、右平移。若前基因和后基因在同一行或者同一列,则上、下、左、右移动,否则删除。在进行这些操作后,基因在对应的空间位置会出现不连续情况,需要对基因进行增添操作使其连续,这样又可能造成染色体变长,故还需要对染色体末端进行删除部分基因的操作。图5 所示的是一个搜索路径步长为6 单元的染色体且共有2 种可能的变异过程,图6 所示为变异操作的总体流程。

图5 染色体变异过程Fig.5 The process of chromosome mutation

图6 变异操作总体流程Fig.6 Flow chart of overall mutation
4 仿真实验
4.1 单舰搜潜
限定整个搜潜过程总的时间步长K=10,定义每个步长为搜索者从一个单元格到相邻单元格所需的时间,搜潜范围为3×3 的9 个单元格,从左到右、从上到下编号依次为1~9。以下基于此设定进行单舰搜潜路径的仿真。
考虑简单的单个搜索者搜潜情况,且此搜索者探测范围仅限制其所在单元格,即(k)=j。因为整个搜潜范围内只有一个搜索者,故不需要对搜潜范围进行区域划分。实验中,对搜索者的搜潜速度进行限制,速度大小是每个步长只能移动到相邻的单元格内。假设搜索者有非常良好的搜潜能力,当潜艇和搜索者处于同一单元格内时,即认为搜索者搜索到了该潜艇。
设定潜艇目标最开始时在第9 个单元格,潜艇每步留在原地的概率为0.4,向其他相邻单元格转移的概率之和为0.6,且向每个单元栅格转移的概率相同。
设定进化算法种群大小为40,迭代次数为1 000,交叉概率和变异概率分别为0.8 及0.2,经过多次试验,可以得到从不同单元格作为初始位置时的搜潜路径。表2 所示为初始位置为第1 个~第9 个单元格的实验结果。

表2 单舰搜潜实验结果Table 2 Results of single ship searching for submarine
4.2 多舰搜潜
在本节中,有多个搜索者在搜潜区域内对移动的目标潜艇进行搜索,设定搜索区域被划分为10×10 的单元格,总的搜潜时间步长K=16。
假设现有3 个搜索者,每个搜索者的观测范围为包括其所在单元格和周围的8 个单元格。实验中,假定搜索者的速度为一个步长,且只能移动到相邻单元格,搜索者在被划分到的区域内的搜索概率为0.8。惩罚函数中的参数设置为b=2.5 ,β=6 ,搜索者自身信号强度SE=4.3 dB,周围8 个单元格的信号强度为3.4 dB。
在整个搜潜区域分布均匀的情况下,初始化概 率 分 布 为-π( )0|0 ,最大化搜潜命中概率的期望值。每个搜索者在被分配的区域内对目标进行探测,并且只考虑搜索者在每个时间间隔内向四周相邻单元格移动的情况,目标留在原地概率为0.2,向其他单元格移动的总概率为0.8,且向各个方向移动的概率相同。
实验中,种群的最小值为40,最大值为60,交叉概率为0.8,分割次数为2 次,变异概率为0.2,迭代次数为1 000。图7 所示为某次实验得到的搜潜路径。在直觉上,搜索者都是朝概率分布更高的方向移动,总体上搜潜路径符合此直觉,但仍然有小部分搜潜路径效率不高,随着迭代次数增加,可能会得到更好的路径。
最优基因的适应度值,即整个搜潜过程的目标命中概率期望值为0.9358,第1 个搜索者的搜潜路径为:
[7,2][8,2][8,3][7,3][7,2][6,2][5,2][5,1]
[6,1][6,0][7,0][8,0][8,1][8,2][9,2][9,3]
第2 个搜索者的路径为:
[1,2][1,1][1,0][2,0][2,1][2,2][1,2][1,3]
[1,4][1,5][1,6][1,7][1,8][2,8][2,7][2,6]
第3 个搜索者的路径为:
[6,7][6,6][7,6][8,6][9,6][9,7][8,7][8,8]
[7,8][6,8][6,7][5,7][5,6][5,5][6,5][7,5]
在此最大搜潜目标命中概率下,上述3 个搜索者的路径即为它们各自的最优路径。
图7 给出了k=1,6,11,16 时刻的目标概率分布。其中,黄色格子的是搜索者所在的单元格。k=1 时,搜索者周围的蓝色格子表明每个搜索者的探测区域,在接下来的几个时刻,搜潜目标概率较低的蓝色区域表明此区域刚刚被搜索者探测过,而红色则表明目标存在于此地的概率较高。
4.3 常规方法对比研究
对于常规搜潜方法,即指水面舰艇编队以间隔均匀的横队队形排列后进行搜潜。该方法的搜潜效能由式(23)[12]评估得到。由此公式可以计算舰艇编队对目标的搜索概率,并得到舰艇编队搜潜的效率。

式中:U搜索为编队整体搜索能力;T延误为搜潜行动开始前延误的时间;T搜索为搜潜时长;V潜艇为估计的潜艇最大速度。在保证其他参数相同的情况下,可以得到2 艘舰艇在常规搜索模式下。搜潜目标的命中概率为0.703 4,当有5 艘舰艇在常规模式下搜索时,相应的概率为0.917 2。而采用本文方法得到的最优搜潜路径进行搜索时,使用3 艘舰艇对潜艇目标搜索到的概率可以达0.935 8。这表明本文方法可以用更少数量的舰艇搜潜取得更高的目标命中概率,大幅提高了水面舰艇编队的搜潜效率。

图7 在k=1,6,11,16 时刻的搜潜目标命中概率分布图Fig.7 The detecting probability distribution of searching submarine when k=1.6,11,16
4.4 分割次数比较
为了确定分割次数对搜潜命中概率期望值的影响,在总的搜潜时间步长为K=16,在搜潜海域为10×10 和16×16 的单元格区域内,实验中采用不同的分割策略来研究分割次数对优化目标的影响。实验采用4 种不同的分割策略如下:不分割;在K=1 时 分 割1 次;在K=1,9 时 分 割2 次;在K=1,5,9,13 时分割4 次。
实验中设置3 个搜索者,全部参数均与多舰仿真采用的相同。
EA 算法种群数量为40,交叉和变异概率分别为0.8 和0.2,迭代次数在1 000/Q~10 000/Q之间,其中Q表示对应的分割次数,采用4 种分割策略分别做100 次试验,得到实验的统计结果如表3 所示,其中ED 表示搜潜目标命中概率期望值。
从表3 可以看出,在没有分割时,得到了比分割一次更好的结果,因为在没有分割时搜索者在整个搜潜范围内没有移动区域限制,但会因整个搜潜范围过大,搜潜周期过长而很难找到最优路径;而当对区域进行分割时,搜索者可以很容易得到在搜索区域范围内的近似最优路径[13],但这也限制了搜索者的移动范围,所以单次分割情况下未取得比不分割时更好的方案。
综上,为了得到更优的搜潜路径,需要在搜潜过程中不时地重新划分搜潜区域,这样不但限制了搜索者的搜潜区域范围,还有利于找到被划分区域内的最优路径,以及保证搜索者有更多的移动方向,从而在整体上得到更优的搜潜路径。

表3 分割次数比较Table 3 The effect of different times of divisions on experimental results
5 结 语
本文利用隐式马尔科夫链建立了水面舰艇编队应召搜潜模型,对搜索区域进行随机划分,并且将舰艇分配到不同子区域,每艘舰艇在被划分的区域内以最大搜索目标命中概念期望值为优化方向,得到在该区域内的最优搜潜路径。此外,采用EA 算法,通过交叉和变异操作过程生成新的可行解,避免了陷入局部最优,使最后得到的搜索路径整体最优。本文将所提方法与常规搜潜方法对比,证明该方法的搜潜概率更高,并且实验也证明了使用不同的分割策略可以得到更优的搜潜路径。

