考虑导弹速度变化的攻击时间和攻击角度控制滑模制导律

吴 放,常思江,李新华

(1.南京理工大学 能源与动力工程学院,江苏 南京 210094;2.西北工业集团有限公司,陕西 西安 710043)

随着现代防御系统兴起[1],仅要求导弹以最小脱靶量击中目标的传统制导律已不足以满足现代战争需求。因此,需要研究一种能够对导弹攻击时间和攻击角度进行控制的制导律,以提升导弹的突防和毁伤能力。

攻击时间和攻击角度控制制导律最早由文献[2]提出,随后众多学者基于不同理论对其进行了研究[3-9]。文献[3]采用模型预测静态规划算法,提出了能够同时控制弹群攻击时间和攻击角度的协同制导方法。文献[4]对网络化导弹的协同攻击问题进行了研究,基于偏置比例导引法设计了带落角约束和攻击时间约束的制导律。文献[3-4]在设计制导指令时均需要估算导弹剩余飞行时间,而估算精度将对导弹命中精度造成不良影响[10-11]。为避免估算误差对制导律的影响,文献[5]基于成型理论,设计了无需剩余飞行时间的攻击时间和攻击角度控制制导律。

由于滑模控制理论具有抑制外界干扰且能够使系统快速收敛的优点,在设计制导律时有较大优势,因此近年来被大量文献应用。文献[6]通过构造视线角速率表达式,基于二阶滑模理论设计了攻击时间和攻击角度控制制导律,但其制导指令形式较为复杂。文献[7]以实际攻击时间与所需攻击时间之差作为切换条件,将制导律在攻击时间控制制导律和攻击角度控制制导律间切换,实现了攻击时间和攻击角度控制,但由于需要估算剩余飞行时间,故存在一定误差。

上述文献均假设导弹速度恒定,但在实际工程应用中,导弹速度往往难以保持恒定。现有攻击时间控制制导律或攻击角度控制制导律对导弹速度变化的解决方法可分为两种。第一种是设计导弹切向加速度,控制导弹速度变化。如文献[12]基于理想比例导引法设计了导弹速度可控的攻击时间控制制导律,并通过反馈线性化增加制导律的鲁棒性。第二种是将导弹速度变化作为干扰项,设计对其不敏感的制导律。如文献[13]提出了一种仅需要导弹速度范围的剩余时间估算方法,基于积分滑模理论设计了攻击时间控制制导律。然而,现有文献中对导弹速度变化时的攻击时间和攻击角度控制制导律研究较少,如文献[9]根据所需攻击时间与导弹实际速度构造标称剩余航程,将导弹控制问题转化为导弹实际剩余航程对标称剩余航程的跟踪问题,从而实现导弹速度变化情况下攻击时间和角度的控制。

针对上述问题,本文对导弹速度可控的攻击时间和攻击角度控制问题进行了研究。考虑导弹与目标的相对运动关系,设计了导弹的切向加速度以控制导弹速度变化。利用成型理论设计同时满足攻击时间和攻击角度控制的理想视线角变化律,基于非奇异终端滑模理论设计制导指令使实际视线角按照理想规律变化,从而实现对攻击时间和攻击角度的控制。

1 问题描述

考虑导弹与目标的二维运动学关系,如图1所示,图中,下标M,T分别表示导弹和目标;下标R表示相对量。假定导弹速度为vM,法向加速度为aM,切向加速度为aτ,目标速度为vT,导弹与目标相对速度为vR。r,γ,θ,φ分别为弹目距离、弹道角、视线角和前置角;θf为导弹击中目标时所需的攻击角度。所有角度以逆时针方向为正。

图1 导弹与目标运动学关系

导弹与目标运动学关系为

(1)

(2)

(3)

(4)

由图1还可得如下关系:

vR=vM-vT

(5)

φR=γR-θ

(6)

(7)

(8)

aM=cos(γR-γM)aR

(9)

根据式(5)、式(6)所示的相对关系,可将式(1)、式(2)简化为如下形式[14]:

(10)

(11)

若通过合理控制导弹的切向加速度aτ,改变导弹速度vM,则能够保持相对速度vR不变。此时可将运动目标的制导问题转化为静止目标的制导问题。导弹切向加速度表达式为

(12)

综上,本文研究的问题可以描述为设计导弹切向加速度和法向速度,使导弹与目标的相对速度保持不变,并在所需攻击时间td以所需攻击角度θf击中目标,即满足如下关系式:

(13)

2 制导律设计

本文将成型理论和非奇异终端滑模理论结合,设计了满足攻击时间和攻击角度同时控制的制导律,设计思路如下:

①基于成型理论设计同时满足攻击时间和攻击角度控制的理想视线角多项式,并通过优化理论计算出多项式的系数,从而确定理想视线角的具体表达式;

②以实际视线角与理想视线角之差作为状态变量,利用非奇异终端滑模理论,设计制导指令使导弹实际视线角按照理想视线角变化,从而实现攻击时间和攻击角度的同时控制。

2.1 理想视线角设计

在设计理想视线角表达式之前,需要说明的是,式(8)、式(10)～式(11)均为关于时间的导数,为便于问题研究,本节需将其转换为关于水平位置x的导数。对任意变量a的转换关系如下:

(14)

根据式(14)所示转换关系,可将式(8)、式(10)～式(11)改写为

(15)

(16)

(17)

基于成型理论设计制导律的主要思想是找到一个理想的视线角变化曲线,通过增大或减小视线角以改变导弹弹道,使导弹能够在所需的攻击时间以所需的攻击角度击中目标。在设计理想视线角变化规律的多项式时,存在多种满足期望条件的候选函数[5-6,10-11]。为简单起见,本文设计如下理想视线角速率多项式:

(18)

式中:σi(i=1,2,…,5)为常数,x0为导弹与目标初始水平距离。

对式(18)积分,得到理想视线角多项式为

(19)

对式(18)关于xR求导数,得:

(20)

θd(xR=0)=θ0

(21)

(22)

为保证导弹击中目标,视线角速率必须在导弹到达目标位置时为0,故有:

(23)

为满足攻击角度控制,在击中目标时,视线角应满足如下条件:

θd(xR=x0)=θf

(24)

将式(21)～式(24)所示边界条件代入式(18)～式(19),解得:

(25)

σ1取任意值时,根据式(25)所示的多项式系数计算理想视线角,若导弹按照理想视线角飞行,则能够以所需的攻击角度击中目标。为了保证导弹在所需攻击时间击中目标,本文通过调整σ1值,以调整视线角变化规律,从而满足:

timp→td

式中:timp为导弹击中目标时的飞行时间,td为导弹所需攻击时间。

为确定σ1的取值,可采用单纯形法等优化方法求解最优σ1值。设计优化目标函数如下:

J=|timp-td|

在优化过程中,当J<0.01 s时终止优化。对于本文算例,取σ1的初值为0.001,得到最优σ1值的平均优化迭代次数为12次。由于优化迭代次数较少,优化速度快,因此在实际工程应用中,可在线计算σ1值。

2.2 制导指令设计

以实际视线角θ与所设计视线角θd之差作为状态变量,即:

e=θ-θd

根据非奇异终端滑模理论[15]设计滑模切换面为

(26)

式中:β>0;p和q为正奇数,p>q。

对式(26)关于x求导数,得:

(27)

(28)

将式(28)代入式(27),得:

(29)

(30)

(31)

式中:M为设计参数,取M>0。sgn(·)为符号函数,定义为

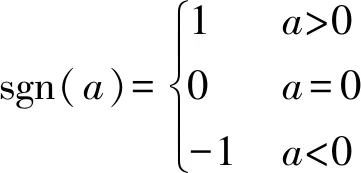
由式(30)、式(31)可得满足攻击时间和攻击角度控制的相对加速度为

(32)

将式(32)代入式(9),可得导弹的法向加速度指令为

2.3 稳定性证明

为证明在所设计制导律作用下,导弹能够实现攻击时间和攻击角度控制,本节将证明制导律在Lyapunov意义下的稳定性。

选择如下Lyapunov函数:

(33)

对式(33)关于x求导,得:

(34)

将式(29)、式(32)代入式(34),得:

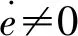
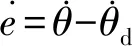
(34)

(35)

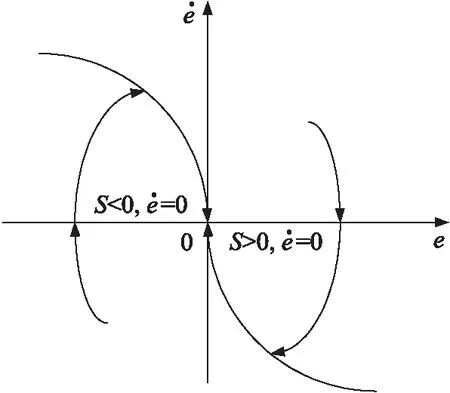
图2 系统的相轨迹

综上可知,本文制导律满足Lyapunov稳定性条件,系统能在有限时间内收敛,导弹视线角按理想视线角变化,能够实现攻击时间和攻击角度控制。

3 数值仿真

本节将选择不同攻击时间和不同攻击角度,对所设计制导律进行数值仿真,以验证其有效性。在进行数值仿真前需要说明,为避免加速度指令因符号函数sgn(·)的不连续而产生抖动,采用连续函数sgmf(·)代替符号函数sgn(·),定义如下:

式中:b为正常数,本文取b=0.1。

数值仿真基本参数如下:导弹初始位置(xM0,yM0)=(0,0),目标初始位置(xT0,yT0)=(7 km,7 km),导弹初始速度vM0=300 m/s,目标速度vT=150 m/s,导弹初始弹道角γM0=45°,目标初始弹道角γT0=10°,导弹最大加速度aMmax=100 m/s2。

制导参数M=300,p=5,q=3,β=1。仿真曲线如图3和图4所示。定义攻击时间误差εtd为实际攻击时间与所需攻击时间之差的绝对值,攻击角度误差εθf为实际攻击角度与所需攻击角度之差的绝对值。表1和表2为不同条件下的攻击时间误差和攻击角度误差。

图3 θf=-60°时的仿真曲线

图4 td=50 s,θf=±45°,±60°时的仿真曲线

表1 θf=-60°时不同攻击时间的攻击时间误差和攻击角度误差

表2 td=50 s时不同攻击角度的攻击时间误差和攻击角度误差

图3为θf=-60°,td=45 s,55 s,60 s,65 s时的数值仿真曲线。表1为攻击时间误差和攻击角度误差。由仿真结果可知,导弹在本文制导律的作用下,均以所需攻击时间和攻击角度击中目标。图3(a)给出了导弹和目标的飞行轨迹。如图所示,增大所需攻击时间,会导致导弹弹道轨迹的曲率增加,导弹需要增加飞行距离以增大飞行时间。弹目距离随时间的变化如图3(b)所示。图3(c)给出了导弹视线角的变化规律,由图可知,击中目标时导弹的视线角符合所需攻击角度的要求。导弹的速度变化曲线如图3(d)所示。导弹速度均先增大后减小,不同的是,所需攻击时间越大,速度达到最大值所需的时间越长。导致速度变化的切向加速度如图3(e)所示,其变化规律符合导弹的速度变化规律,达到最大速度之前,攻击时间越大,则导弹切向加速度越小。图3(f)所示为导弹法向加速度曲线,由图可知,导弹法向加速度均为超过最大加速度限制,且在击中目标时收敛为0。

图4所示的为td=50 s,θf=±45°,±60°时的数值仿真曲线,表2为攻击时间误差和攻击角度误差。仿真结果表明,导弹均以所需条件击中目标,验证了本文制导律的有效性。导弹切向加速度在所需攻击角度θf为负时的变化幅度小于θf为正时的变化幅度。在切向加速度的作用下,当θf为负时,导弹速度先增大后减小;当θf为正时,导弹速度进行了两次先增后减。由于导弹初始前置角为正,故θf为正时,导弹需要更大的机动能力调整弹道以满足所需攻击时间和攻击角度,由图4(f)可知,θf=45°,60°时的控制能量大于θf=-45°,-60°时的控制能量,但法向加速度均在击中目标时收敛为0。

4 结束语

针对考虑导弹速度变化的攻击时间和攻击角度控制问题,本文将成型理论和非奇异终端滑模理论相结合,设计了一种能够控制攻击时间和攻击角度的制导律,同时对导弹的速度进行了控制。所设计制导律无需估算剩余飞行时间,避免了估算产生的误差,适用性更强。通过理论推导,证明了该制导律满足攻击时间和攻击角度控制的Lyapunov稳定性条件。针对不同所需攻击时间和攻击角度进行了数值仿真,结果表明,该制导律能够较好地实现攻击时间和攻击角度控制。