基于ESO的拦截机动目标带攻击角度约束制导律

张宽桥,杨锁昌,刘 畅

(陆军工程大学 石家庄校区导弹工程系,河北 石家庄 050003)

在现代战争中,很多导弹需要以一定的攻击角度命中目标,来增加战斗部的毁伤效能。1973年,KIM首次将攻击角度约束问题引入制导律设计中。其后经过40多年的发展,针对带攻击角度约束制导律的研究成果丰硕[1]。由于滑模变结构控制在滑动模态对干扰具有不变性,因此被广泛应用在制导律设计中。文献[2]采用弹目视线角速率和攻击角度约束项作为滑模面,结合自适应指数趋近律,设计了带攻击角度约束的滑模制导律。

传统滑模制导律采用线性滑模面,不能使系统状态有限时间收敛至平衡点,而终端滑模控制能使系统状态有限时间收敛[3]。文献[4]基于终端滑模控制,提出了带攻击角度约束的有限时间收敛制导律,使系统状态有限时间收敛至平衡点,但制导指令中含有负指数项,会存在奇异问题。文献[5]改进了一种非奇异终端滑模面函数,解决了奇异问题,提出了非奇异终端滑模控制方法。文献[6]基于非奇异终端滑模控制,提出了带攻击角度约束的制导律。文献[7]进一步提出了一种快速收敛的非奇异终端滑模面,具有比传统非奇异终端滑模更快的收敛速度。

导弹自动驾驶仪并非一个理想环节,它存在延迟等动态特性,会一定程度上影响导弹的制导性能,因此在制导律的设计中需要加以考虑。文献[8]将自动驾驶仪近似为一阶环节,基于非奇异终端滑模控制和动态面控制来设计制导律,具有良好的制导性能。实际上,导弹自动驾驶仪一般具有高阶动态特性。若将其近似为高阶环节,能够很好地模拟驾驶仪的动态特性,但这会使制导律的形式过于复杂。为解决这个问题,有学者将驾驶仪近似为二阶环节,在贴近驾驶仪实际动态特性的同时,降低制导律形式的复杂程度。文献[9]考虑导弹自动驾驶仪二阶动态特性,基于动态面控制设计制导律,并未考虑攻击角度约束问题。

本文针对攻击角度约束的问题,选取了一种带攻击角度约束项的非奇异快速终端滑模面,将导弹自动驾驶仪动态特性近似为二阶环节,提出了带攻击角度约束的新型制导律。该制导律不但克服了文献[4]中制导律存在的奇异问题,还提高了系统状态的全局快速收敛性,实现了对自动驾驶仪动态特性的有效补偿。针对目标加速度未知的问题,本文还设计了超螺旋扩张状态观测器对目标加速度进行估计。仿真表明,所设计制导律能够满足命中精度和攻击角度约束的要求。

1 弹目相对运动模型

假设导弹和目标均为质点,在二维惯性坐标系上建立弹目相对运动几何关系图,如图1所示。图中,vm和vt为导弹和目标的速度,假设为常值;θm和θt为导弹的弹道倾角和目标的航迹倾角;r为弹目相对距离,q为弹目视线角。

图1 弹目相对运动关系

因此,可构建弹目相对运动方程为

(1)

(2)

(3)

(4)

式中:ηm=q-θm,ηt=q-θt。

对式(2)求导,并结合式(1)得:

(5)

式中:atq=atcosηt,视为有界未知量来处理。

攻击角度为导弹击中目标时导弹与目标速度矢量方向之间的夹角,攻击角度约束问题可以转化为终端视线角约束问题。自动驾驶仪的动态特性对导弹的制导效果有很大的影响,需要加以考虑。导弹自动驾驶仪可用二阶动态特性来描述[10],表达式为

(6)

式中:ξ为导弹自动驾驶仪的阻尼比,ωn为自振频率,ac为导弹制导指令。

考虑自动驾驶仪动态特性带攻击角度约束的弹目相对运动模型可描述为

(7)

2 超螺旋扩张状态观测器

在制导过程中,目标的加速度信息往往是无法进行测量的,因此需要对目标机动等信息进行估计。扩张状态观测器(extended state observer,ESO)是一种很好的估计系统不确定性的方法[11]。但传统的ESO在设计时,将总扰动视为常值或者是慢变的量,故总扰动的导数为0。在估计时变扰动的时候,这种处理方式阻碍了ESO性能的进一步提升。虽然针对时变的干扰,可以增大ESO的增益来获得满意的干扰估计效果。但是,当系统的输出存在测量噪声时,高增益会带来测量噪声的放大问题。借鉴ESO设计思想,将二阶滑模超螺旋算法[12]与ESO相结合设计一种超螺旋扩张状态观测器(STESO),具有ESO和滑模控制的优点,且采用超螺旋算法能够降低滑模控制的抖振现象。

考虑如下一阶系统:

(8)

式中:Y为系统输出,u为系统输入,w(t)为总扰动。

|ζ|≤ζu

(9)

式中:ζu为ζ的上界。

定义新的状态变量y1=Y,y2=w(t),则式(8)可描述为

(10)

基于超螺旋算法改进扩张状态观测器,在超螺旋算法中引入了线性项,进一步加快观测器的收敛速度,设计STESO为

(11)

结合式(10)和式(11)可得:

(12)

为证明方便,引入如下引理。

针对如下非线性系统:

(13)

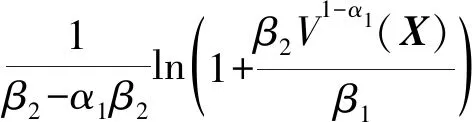
证明定义一组新的状态变量:

(14)

微分得:

(15)

式中:

(16)

定义Lyapunov函数:

V1=YTPY

(17)

(18)

易证P为正定矩阵,则下式成立:

λmin(P)‖Y‖2≤V1≤λmax(P)‖Y‖2

(19)

式中:λmax(P)和λmin(P)为矩阵的最大和最小特征值。

对式(17)微分得:

(20)

式中:

(21)

易证Q1为正定矩阵。由式(16)和式(18)可得:

(22)

定义Q=Q1+Q2,将式(22)代入式(20)得:

(23)

式中:

(24)

选取如下参数:

(25)

易证Q为正定矩阵。

由式(19)可知:

(26)

式(23)可转化为

(27)

针对式(5)可以建立如下STESO:

(28)

式中:z2为atq/r的估计值。

3 带攻击角度约束制导律

(29)

式中:k1>0,k2>0,α=p1/p2>1,β=p1/p2,1<β<2,p1、p2、p3、p4均为奇数。

当系统到达滑模面后,即:

(30)

则x1和x2可有限时间收敛至原点,且比传统非奇异终端滑模的收敛速度更快。具体证明参考文献[7]。

为削弱抖振,同时加快滑模趋近速率,增强制导律的自适应性,选取如下指数幂次趋近律:

(31)

式中:k3>0,k4>0,γ>0。

相比传统的指数趋近律,趋近律(31)的系数可随弹目距离的变化而自适应地调整。当弹目距离较大时,趋近律系数较小,制导指令较小,保证了导弹的飞行稳定性;弹目距离逐渐减小时,系数增大,收敛速度加快,保证了制导精度的要求。

定理2基于滑模面(29)和趋近律(31),利用STESO对目标加速度信息进行估计,采用动态面控制方法设计考虑导弹自动驾驶仪动态特性的攻击角度约束制导律为

(32)

x3c和x4c为虚拟控制指令,τ3和τ4为滤波器的时间常数,τ3>0,τ4>0,则滑模面S1能在有限时间内收敛至区域|S1|≤δ,其中δ为一较小正数。同时系统状态x1和x2能够在有限时间内收敛至区域:

(33)

证明定义边界层误差:

σi=xid-xic,i=3,4

(34)

微分得:

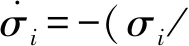
(35)

选取Lyapunov函数:

(36)

微分得:

(37)

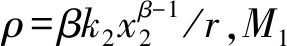
将式(37)整理后得:

(38)

(39)

求解式(39)得:

0≤V2(t)≤1/(4K)+[V2(0)-1/(4K)]e-2Kt

(40)

由式(40)和引理3可知,V2是有限时间稳定且有界的,因此,S1、S2、S3、σ3和σ4是有界的。若参数选择适当,可使它们任意小。因此必然存在一个较小正数δ,使得在制导律(32)的作用下,滑模面S1可在有限时间内收敛至区域|S1| ≤δ。当S1进入区域|S1| ≤δ,令S1=κ,其中|κ| ≤δ,可得:

(41)

式(41)可进一步写成:

(42)

|x2|≤(|κ|/k2)1/β≤(δ/k2)1/β

结合式(41)可得x1能够有限时间内收敛至区域:

|x1|≤|x1|+k1|x1|α≤k2|x2|β+|κ|≤2δ

证毕。

制导律(32)中存在x3d和x4d需要根据式(32)进行求解。比较k5和1/τ3、k6和1/τ4的参数取值范围,可以发现其取值范围基本重合,因此可以令k5=1/τ3,k6=1/τ4,此时既可以消去制导律(32)中的x3d和x4d项,又可以减少制导律中的参数数量,且不影响其整体性能。简化后的制导律形式为

(43)

为叙述方便,将式(43)所示的考虑自动驾驶仪动态特性的滑模制导律简记为ADNTSMG。

4 仿真分析

本节基于弹道仿真,对所设计制导律的性能进行对比仿真研究。导弹和目标的初始位置分别为(0,0)和(15 km,10 km),导弹的速度为vm=800 m/s,初始航迹角θm=45°,目标运动速度vt=300 m/s,初始航迹角θt=180°。导弹过载n=am/g,导弹的最大可用过载为20。设置自动驾驶仪动态参数为ξ=0.8,ωn=8 rad/s。仿真中引入了文献[2]提出的自适应滑模制导律(ASMG)以及文献[6]提出的非奇异终端滑模制导律(NTSMG)进行对比仿真。为验证STESO的性能,引入传统ESO进行对比仿真分析。

根据目标圆弧机动和蛇形机动2种机动方式,分2种情形进行仿真。其中圆弧机动时,at=10 m/s2,蛇形机动时,at=20sin(πt/5)。仿真结果如图2～图6和表1所示,表中,tf为攻击时间,D为脱靶量。

表1 攻击时间和脱靶量的仿真结果

图2为目标加速度的估计曲线,可以看出,STESO相比传统ESO能够更快、更准确地对目标的加速度信息进行实时在线估计,具有较快的收敛特性和较强的鲁棒性。

图2 目标加速度估计

由图3可以看出,在ADNTSMG作用下,导弹的运动轨迹较为光滑,在末段较为平直,这是由于ADNTSMG采用了非奇异快速终端滑模面,使得弹目视线角速率能够在有限时间内快速收敛至0附近。在ASMG的作用下,导弹运动轨迹的曲率整体较大。在NTSMG的作用下,导弹的运动轨迹在制导末段曲率变化较为剧烈。

图3 弹目运动轨迹

由图4可知,ASMG和ADNTSMG能使弹目视线角收敛至90°附近,但ASMG存在抖振和发散现象,主要由于滑模制导律固有的抖振问题和自动驾驶仪动态特性的影响。而ADNTSMG对自动驾驶仪动态特性进行补偿且采用了自适应指数趋近律削弱了抖振现象。NTSMG弹目视线角不能达到期望角度,且逐渐发散。

由图5和图6可以看出,ASMG和NTSMG均不能使弹目视线角速率及导弹过载收敛至0附近,且有抖振现象和发散趋势,这将增大导弹的脱靶量(见表1)。而ADNTSMG能使弹目视线角速率及导弹过载有效收敛至0附近。ADNTSMG在末端需用过载较小,有足够的过载余量应对各种干扰,进而能提高导弹的制导精度(见表1)。由表1可以看出,ADNTSMG的攻击时间和脱靶量明显小于ASMG和NTSMG。

综上所述,ADNTSMG能补偿自动驾驶仪动态特性,攻击时间和脱靶量均小于ASMG和NTSMG,且弹目视线角及角速率能有限时间内收敛至期望值附近,验证了ADNTSMG的有效性及优越性。

图4 弹目视线角

图5 弹目视线角速率

图6 导弹法向过载

5 结束语

本文针对攻击角度的问题,提出了一种带攻击角度约束考虑自动驾驶仪动态特性的滑模制导律。通过理论分析和仿真验证,可以得出以下结论:

①快速收敛的非奇异终端滑模面,能够实现制导系统状态有限时间快速收敛,自适应指数趋近律能削弱抖振,增强滑模控制的自适应性。

②超螺旋扩张状态观测器STESO估计精度高,收敛速度快,能有效估计系统未知干扰。

③考虑自动驾驶仪动态特性的制导律ADNTSMG能够对自动驾驶仪动态特性进行有效补偿,增强制导系统的鲁棒性,提高导弹的制导性能。

制导参数的选取会影响制导律的制导性能,后续还需要针对制导参数优化方面进行研究。