权重归一化拉格朗日插值及其空间降尺度应用

胡沛然，陈少辉

(1.中国科学院地理科学与资源研究所 陆地水循环及地表过程重点实验室，北京 100101；2.中国科学院大学，北京 100049)

0 引言

人们在通过各种手段获取观测数据时，观测仪器记录的要素一般为特定格式的离散资料。由于观测仪器故障、恶劣的环境或其他不可避免的外部因素干扰，观测资料会出现一定数量的缺测值或异常值，使得用户无法正常使用观测数据，这就需要用户选取合适的数学插值方法来填补数据空缺并处理数据的异常值。另一方面，虽然现代的观测技术和观测手段得到了很大进步，用户可以获取各种高质量的观测资料，但是我们的研究尺度往往会和观测资料的尺度无法完全匹配，例如人们获得的卫星遥感图像或气象资料与实际研究区域的空间尺度相差很大，为了和实际的研究精度相匹配，就必须要对观测数据进行插值处理，才能满足数据使用者的特定需求。

拉格朗日插值法最早于1779年由一位英国的数学家提出[1]，后来由于著名科学家拉格朗日在他的一本书中又提到了这个经典的插值方法而得以命名[2]。拉格朗日插值法具有简洁明了的迭代过程和较高的计算精度，因而十分适合通过计算机编程来处理各种数据。近几十年来，拉格朗日插值方法在全球定位系统(global positioning system，GPS)卫星定位[3]、水文气象模型[4]和计算机图像视频处理[5]等领域均有成熟的应用。根据拉格朗日插值方法的理论可以得出，计算结果的精度会随着多项式阶数的增加而大幅提高，但阶数的增加可能会造成龙格现象(runge phenomenon)。具体来说，简单的一阶拉格朗日插值不会带来数值振荡，然而计算结果会出现一定的数值误差，无法达到用户所需要的数值精度。二阶甚至更高阶的拉格朗日插值可以有效减小插值结果的误差，同时也会导致插值区间上出现显著的数值振荡(即为龙格现象)。虽然拉格朗日插值具有诸多优点，但高次插值所引发的龙格现象却在很大程度上限制了该方法在实际中的广泛应用[6]。为了解决这个问题，目前的主要方法有适当增加计算区间边缘插值点个数和分段使用低次插值多项式等。在近年的研究中，Zhang在海洋模型的盐度计算中采用混合一阶和二阶的拉格朗日插值法[7]。Wu等提出了一种混合N阶拉格朗日插值方法[8]，即首先使用N阶拉格朗日插值法进行插值处理，然后在结果误差较大的地方使用低阶拉格朗日插值法进行修正，这种方法对提高插值精度和减小数值振荡有显著效果。熊欢欢等在GPS星历插值计算中采用高阶和低阶组合的滑动插值方法，用以提高插值区间边缘的计算精度和减弱龙格现象[9]。寿媛等使用Multiquadric(MQ)拟插值法和分段线性插值避免高次插值时出现的龙格现象[10]。

在陆面模型进行径流模拟时，研究者发现在对驱动模型的气象强迫数据进行空间降尺度的过程中，原始的拉格朗日插值方法虽然易于编程且计算速度快，但插值效果却呈现出较大波动。增加区间边缘插值点个数和使用混合高低阶插值方法在一定程度上可以有效减弱高阶拉格朗日插值的龙格现象，但这些方法会涉及复杂的判断和较高的计算量，并不适合编程处理大量数据。针对这个问题，本文提出了一种相对简便的改进方法，在满足一定精度的情况下，快速有效地减少了高阶拉格朗日插值方法所带来的数值振荡。

1 方法介绍

1.1 拉格朗日插值原理

拉格朗日插值法的基本原理是通过迭代计算求得一个特定的多项式，其在每个观测点恰好取到给定的观测值。插值方法的定义如下：

对某个多项式，已知有k+1个给定点：(x0，y0)，…，(xk，yk)，假设任意两个xj都互不相同，那么拉格朗日插值多项式为：

(1)

把式中每个lj(x)叫做基函数，lj(x)具体的表达式为[11]：

(2)

从上面的定义中可以看出，拉格朗日插值法原理简单，仅涉及到了简单的迭代计算，基函数的取值只与插值点坐标有关，非常适合理论分析和编程计算。然而在实际的应用过程中，插值多项式会随着阶数的增加而在插值区间边缘产生强烈的数值不稳定的现象，也就是说插值多项式虽然在给定的观测点取到了观测值，但在插值区间边缘附近却会产生巨大的偏差，这被称为龙格现象。如图1所示，虽然多项式在插值区间的(-1，1)这部分精度很高，但是在区间的边缘部分产生了大幅的数值振荡。

图1 插值中的龙格现象

1.2 拉格朗日插值法的一种改进方法

拉格朗日插值方法在高阶插值时会出现显著的龙格现象，在模拟一个较为平稳的函数时，插值多项式的数值不稳定性更加强烈，究其原因是由基函数计算的插值权重所致，为此提出了一种权重归一化方法。数据归一化的主要思想是通过一系列数值计算，把原始数据映射到特定的范围内。数据的归一化计算可以将数据按比例缩放，使其落入一个规定的区间内(例如0～1或-1～1之间)。归一化后既可以保留原始数据的某些特性，又可以消除数据的异常波动，在某种程度上可以提高插值精度。归一化有多种方法，其中一种常用的简单归一化方法定义为：对于正项序列x1，x2，…，xn，进行如下变换：

(3)

本文针对拉格朗日插值方法中的龙格现象，发展了一种基于归一化思想的插值改进方法，通过对插值基函数进行归一化计算将其转换在(0，1)的范围内，减少了多项式在区间内的数值振荡。相比于目前主流的解决思路，新的改进方法在插值计算时简便易行，精度在可接受范围内。具体步骤如下：

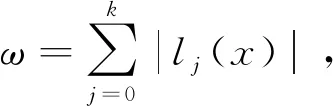
(4)

②将新的基函数ωj(x)带入多项式(1)中，得到改进后的插值多项式如下：

(5)

2 改进前后插值结果对比实验

2.1 插值效果主观对比

为了检验插值方法改进的效果，本文设计了一组主观对比实验。我们从中国区域地面气象要素数据集中选取一片区域(经纬度范围为114.85°E～119.05°E，35.65°N～38.25°N)，并以2001年2月1日12时、2001年4月12日15时、2001年7月22日18时3个时刻的气温(2 m)、气压、向下短波辐射和向下长波辐射数据作为此次实验的样本数据。具体的插值对比方法为：

①考虑到计算精度和效率，采用五阶拉格朗日插值法来进行滑动插值计算，即每次插值计算时，待插值点必须始终位于插值区间的中心。

②使用传统拉格朗日插值方法将样本数据(空间分辨率为0.1°)内插成0.02°的空间分辨率，插值前后的空间范围不变。

③使用本文改进的拉格朗日插值法将样本数据内插成0.02°的空间分辨率，插值前后的空间范围不变。

④通过Fortran语言编写程序来实现数据读取和插值计算，并输出图像直观对比插值方法改进前后的效果。

2.2 插值结果精度分析

上文2.1中的对比实验只是通过插值结果与原始数据的定性图形对比来主观判断插值效果。为了准确地定量比较改进前后插值方法精度的变化，我们在中国区域地面气象要素数据集中取出某一时刻的地面向下长波辐射数据作为定量对比实验的样本数据，样本数据尺寸为172列乘126列(经纬度范围为104.25°E～121.45°E，23.45°N～36.05°N)。将样本数据(图2)重采样至分辨率更低的水平(图3)，随后再将其分别使用原始和改进后的拉格朗日插值法，按照2.1中的五阶滑动插值重新内插为0.1°的空间分辨率。将插值后得到的2组数据分别与样本数据做误差分析，画出相对误差频率直方图进行比较，并选取3个常用的误差指数作为本实验插值精度的评价指标，具体见表1，表中的Xi与Zi分别为样本数据和插值计算后的数据。最后对比原始样本数据和使用改进方法插值得到的结果，进而分析改进方法的误差空间分布特征。

图2 样本数据

图3 重采样数据

表1 实验精度评价指标

2.3 样本数据介绍

中国区域地面气象要素数据集(China meteorological forcing dataset)，是一套以现有的多种再分析资料融合气象观测数据制作而成的气象要素数据集。此数据集由中国科学院青藏高原所研制(寒区旱区科学数据中心http：//westdc.westgis.ac.cn/)，适合驱动陆面过程模型进行模拟计算。数据集在空间上覆盖全国，时间范围上覆盖了1979—2010年，时空分辨率为3 h和0.1°，数据集包含了表2中的7个变量[12]。

表2 数据集变量信息表

3 插值结果分析

图4、图5、图6分别为实验区域3个时刻的近地面气温、气压、向下短波辐射、向下长波辐射样本数据。样本数据的空间分辨率为0.1°×0.1°，颜色越深表示像元的数值越低。从图中可以清晰看出，原始数据集的空间分辨率较低，4个变量在空间上的分布极不连续，呈现出明显的斑块状分布。在使用这种低分辨率气象数据驱动陆面模型进行高分辨率模拟前，必须采用一定的数学方法对原始数据进行降尺度插值计算。

图4 2001年2月1日12时原始数据

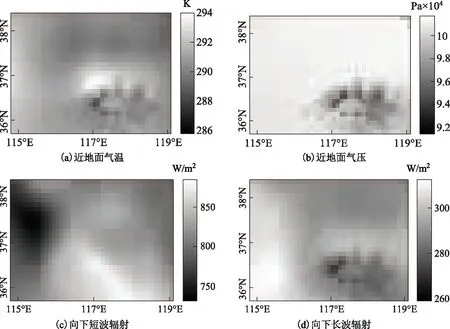
图5 2001年4月12日15时原始数据

图6 2001年7月22日18时原始数据

图7、图8和图9是使用传统拉格朗日插值法将3个时刻的数据内插成空间分辨率为0.02°后输出得到的图像。从图中可以看出插值结果很不理想，在数据的边缘处效果最差。其余部分虽然变化趋势大致同样本数据相同，但仍可以看出有明显的数值波动。出现这种现象是由于拉格朗日插值法在高阶插值时会在插值区间边缘产生龙格现象，尤其是在模拟类似于气象强迫数据这种总体平稳的数据时龙格现象更加强烈。另一方面，在数据起始和结束的边缘区域，数据无法满足滑动插值时待插值点始终位于插值区间中心的要求，故数值误差在边缘处最大。

图10、图11和图12是使用本文改进后的拉格朗日插值法将样本数据内插成空间分辨率为0.02°输出得到的图像。从输出结果可以清晰看出，改进后的插值结果不仅在变化趋势上完全与样本数据吻合，且基本可以有效避免原始插值方法中的缺陷，消除了明显的数值误差。

图7 2001年2月1日12时

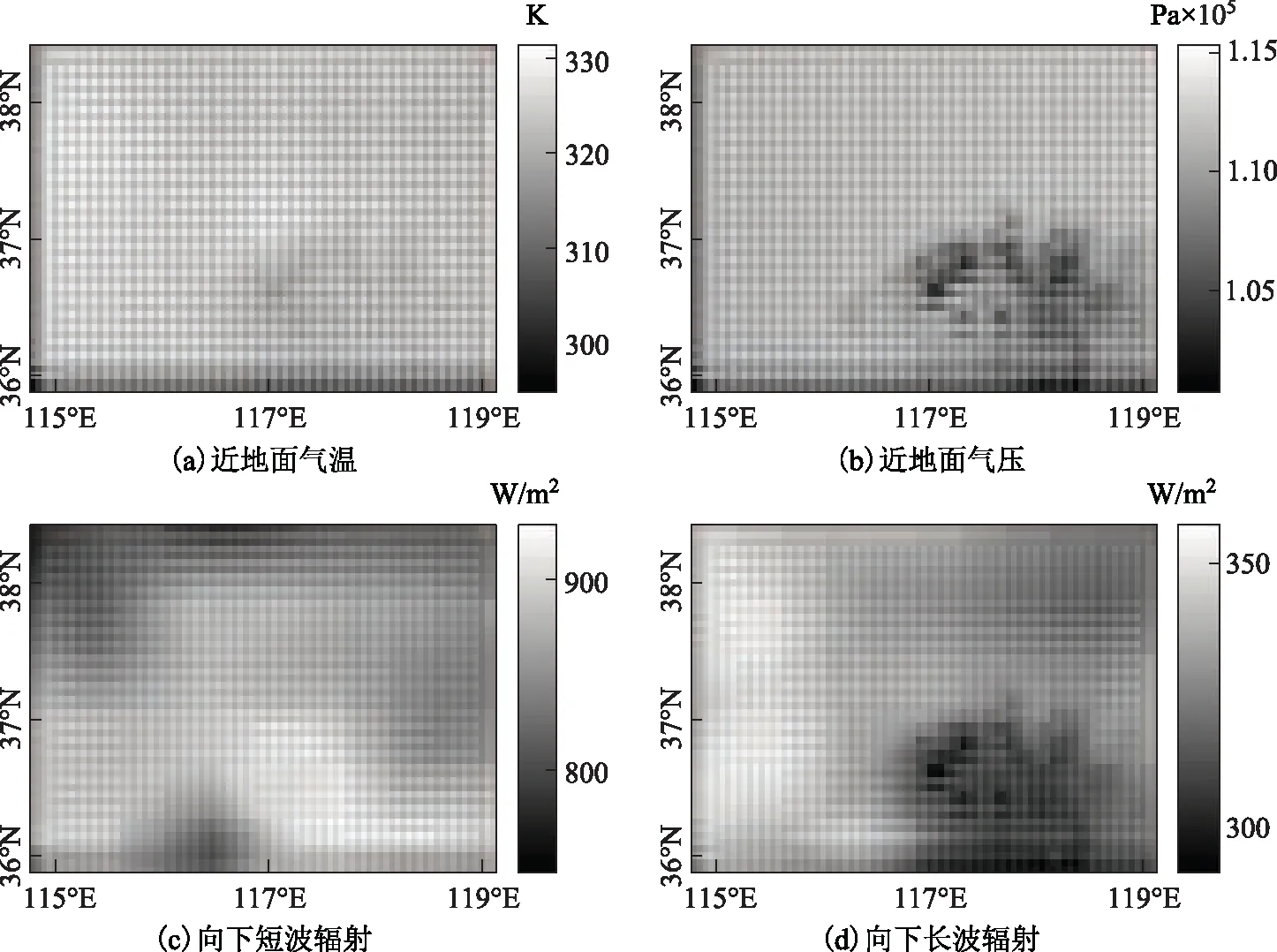
图8 2001年4月12日15时

图13和图14为定量对比实验2.2输出的传统方法和改进方法插值结果。从插值效果上看，原始插值方法产生了大量的数值波动，未能准确模拟出原始数据。而使用改进方法插值得出的结果无论在整体趋势上还是数值精度上，都可以较为真实地反映原始数据的空间分布特征。图15为传统方法和改进方法的误差频率分布直方图。从直方图可以看出，传统方法的相对误差的频率极值出现在0.1附近，相对误差的范围在-0.2到0.5之间，其概率分布无明显规律。而方法改进后的相对误差大致呈现出正态分布，频率极值出现在0附近，相对误差的范围分布在±0.2以内，即改进后的误差范围相比于传统方法缩小了大约一半。从表3中的精度指标数值可以看出，使用改进方法得出的插值结果平均绝对误差(MAE)从传统方法的19.771下降为5.610，平均相对误差(MRE)从8.339下降到2.284，而均方根误差(RMSE)降幅最大，由34.926下降为8.584。通过定量的精度评估可以得出，使用改进的拉格朗日插值方法后，数据的插值精度得到了大幅提高。图16为使用改进方法插值后数据与原始数据的相对误差分布图。通过对比分析，可以看出改进后的拉格朗日插值方法在原始数据数值平稳的地方插值精度较高，相对误差大致控制在10%以内，能够较为准确地反映出原始数据的空间分布特征。但是在数据边缘部分和数据变化较大的地方插值精度较低，其相对误差最高达到了30%，故改进后的拉格朗日插值法不适合用于波动剧烈数据的插值计算。

图9 2001年7月22日18时

图10 2001年2月1日12时

图11 2001年4月12日15时

图12 2001年7月22日18时

图13 传统方法插值结果图

图14 改进方法插值结果

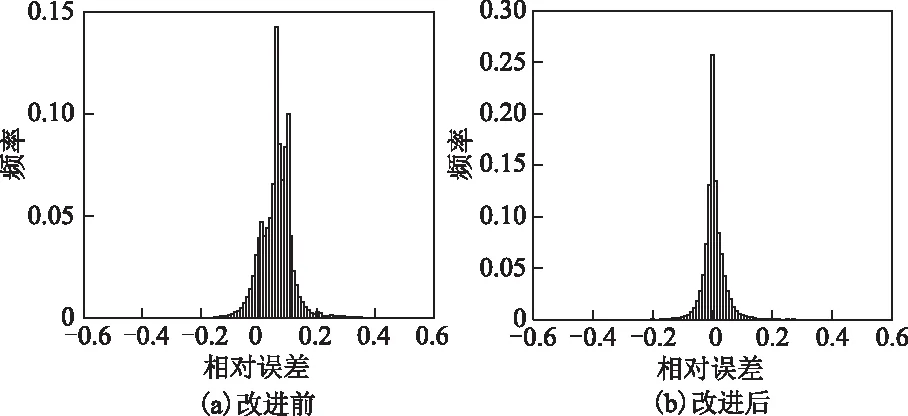
图15 改进前后相对误差频率直方图

表3 拉格朗日插值法精度评价表

图16 改进方法的误差空间分布

4 结束语

通过对上述两个实验的定性比较与定量分析，可以得到以下3点结论：

①原始数据在实际应用时为了和研究精度相匹配，必须综合考虑计算精度和复杂度来选取合适的插值方法，在保证数值精度的前提下进行插值处理。

②拉格朗日插值方法的插值原理简单，公式中仅包含了简单的迭代运算，故十分适合编程来处理数据，当选取合适的阶数进行插值时，插值的精度完全可以满足用户需求。

③拉格朗日插值方法在高阶计算时会发生明显的龙格现象，尤其是在插值类似于气象数据这种相对平稳而又存在局部小幅波动的数据时尤为显著。如果采用滑动拉格朗日插值法时，数据边缘也会产生极大的误差。本文提出的基于归一化思想的改进方法，通过重新计算拉格朗日插值基函数后，因龙格现象产生的误差被有效减弱。改进的拉格朗日插值方法在处理数值上相对平稳的数据时效果比较理想，但不适用于处理数值波动剧烈的数据。因此在陆面模型气象驱动数据空间降尺度时，可选用本文提出的朗格拉日插值改进方法。