非平稳NDVI时序数据人工神经网络建模方法

赵健赟，彭军还，宋芊，张波

(1.青海大学 地质工程系，西宁 810016；2.中国地质大学(北京) 土地科学技术学院，北京 100083；3.北京麦格天宝科技股份有限公司，北京 100043)

0 引言

全球变化及其带来的各种生态环境问题受到各国政府和国际组织越来越多的关注，已经成为地球科学领域的研究热点之一[1-5]。植被作为陆地生态系统的重要组成部分，是连接大气和土壤的重要纽带，植被覆盖是区域环境、地理条件和气候变化等多种因素作用的结果，植被覆盖变化是全球变化的重要指示器[6-7]。

归一化植被指数(normalized difference vegetation index，NDVI)与植被绿度、物候、光合作用紧密联系，是反映全球或区域植被环境变化的重要指标。目前，MODIS、AVHRR、SPOT、TM/ETM等卫星传感器均提供不同时空分辨率的NDVI时间序列产品，已有很多学者利用NDVI产品对全球或区域的植被覆盖时空变化进行了研究[8-13]，如邓兴耀等[12]利用GIMMS NDVI对中亚干旱区植被覆盖的时空变化进行了研究，申丽娜等[10]利用GIMMS NDVI3g对三北防护林的植被覆盖变化图谱进行了分析，郭继凯等[11]利用MODIS NDVI对塔里木河流域植被覆盖变化及其驱动因素进行了研究等。

但是，目前大多数研究利用NDVI时间序列数据进行植被覆盖变化分析时，仅对其进行线性建模，掩盖了地理现象和过程的真实特征，未考虑NDVI时间序列的非平稳性[14-16]。处理非平稳序列的传统方法是先利用对数、差分等算法将其平稳化后，再利用自回归滑动平均(autoregressive and moving average，ARMA)进行建模处理[17-21]。随着机器学习及人工智能技术的迅速发展，人工神经网络、支持向量机、遗传算法等为时空非平稳序列建模提供了新的方法[22-26]。本文基于人工神经网络(artificial neural network，ANN)模型，研究顾及NDVI数据非平稳特性下的时间序列建模方法，利用GIMMS NDVI3g数据对青海省1982—2015年的植被覆盖变化进行建模，并对其未来变化进行预测。

1 数据和研究方法

1.1 数据资料

选用美国国家航空航天局提供的1982—2015年15天合成8 km分辨率AVHRR GIMMS NDVI3g数据集。该数据集融合了NOAA-7/9/11/14/16/17/18/19的AVHRR/2和AVHRR/3两种不同传感器数据，并且进行了轨道偏移、大气水汽、辐射、气溶胶、除云、几何畸变等校正与处理[27]。

选用中国科学院计算机网络信息中心国际科学数据共享平台的青海省行政区划数据，对NDVI3g数据集进行裁切获得青海省NDVI数据集，并利用SG滤波算法对数据集进行降噪处理[28]。

选用美国航天航空局 SRTM 90 m DEM Version 4共 8景DEM 数据，对其进行拼接、裁切等处理后形成青海省DEM 数据。

以上数据均采用Albers Conical Equal Area投影(南标准纬线：25°S；北标准纬线：47°N；中央经线：105°E)。

1.2 时间序列数据的非平稳性

平稳时间序列数据一般指序列数据中不包含趋势、周期等变化特征，即期望或均值为常数，其方差、协方差等统计量不随时间和空间的变化而发生改变[29-34]。设t时刻i位置的观测值均值为：

μzi(t)=E[zi(t)]

(1)

若时间序列平稳，则在(t+k)时刻(i+h)位置满足：

(2)

若不满足式(1)、式(2)，则该数据为非平稳序列。

1.3 非平稳NDVI时间序列模型方法

时间序列过程一般由总体确定性变量和局部随机变量构成，总体变异即为变化趋势，而局部变异是在时间序列过程中分离出总体趋势后的随机变异量，局部变异量一般为平稳过程。因此，一个NDVI序列过程可用下式表示[35-36]：

(3)

式中：NDVIi(t)为t时刻i位置的NDVI观测值；μi(t)为数学期望总体趋势；f(i，t)为非线性函数；ei(t)为随机变异量。本文提出基于ANN与ARMA组合的NDVI时间序列模型，流程如图1所示。

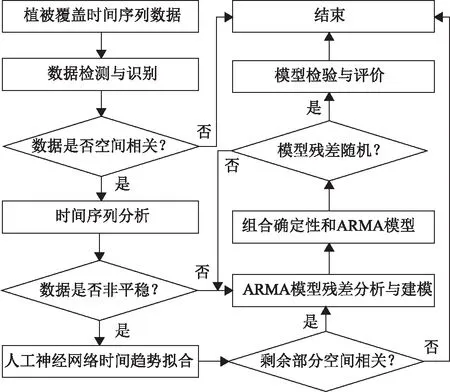
图1 基于ANN与ARMA的NDVI序列建模流程

考虑到ANN模型具有自组织、自学习能力和较强的非线性和容错性，比较适合于解决复杂的非线性动态问题[37]，可以直接建立基于ANN非线性NDVI时间序列模型，其中包含一个隐含层、一个输出层的ANN函数模型如下[38-40]：

(4)

非平稳NDVI时间序列数据建模，涉及到确定ARMA模型和非线性ANN模型参数的问题，选用最小信息准则(akaike information criterion，AIC)估计最佳模型参数：

(5)

2 NDVI时序数据建模结果与分析

2.1 NDVI时间序列数据的非平稳性检验

基于青海省GIMMS NDVI3g数据，在像元、区域级别分别构建15天、年尺度NDVI时间序列。为描述构建的NDVI序列数据特性，绘制对应的QQ图(正态概率图)[31-32，36，41]，结果如图2所示。利用小波时序分析方法[42-45]，对像元级别的时间序列进行周期特征和趋势特征进行分解，结果如图3所示。

图2 NDVI序列正态性检验

图3 NDVI序列季节和趋势特征分解

从图2、图3可以看出，时间序列数据均不符合正态分布，显然不满足式(1)、式(2)的平稳条件，数据序列具有明显的趋势特征，且像元级别的时间序列数据具有显著的周期变化特征。因此，NDVI3g数据在像元、区域级别上均具有明显的非平稳特性。

2.2 NDVI时间序列数据的非平稳建模

利用ANN与ARMA组合模型、ANN非线性模型对像元年际序列数据进行分析，获得2种模型参数的AIC指标如表1所示。

表1 像元年际尺度的2种模型AIC指标

按照最小信息准则，确定组合模型的参数为(6，6)，非线性ANN模型的参数为(4，1，1)。利用上述参数分别建立ANN-ARMA组合模型和非线性ANN模型，结果如图4所示。

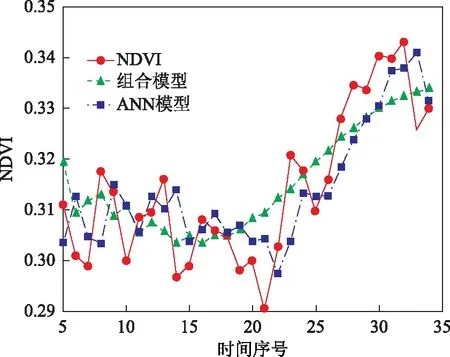
图4 像元尺度的组合模型与ANN模型

由建立的NDVI时间序列模型可以看出，2种模型均能较好地模拟和反映NDVI变化情况。组合模型较为光滑，能够凸显植被的总体变化趋势，而非线性ANN模型与观测值更为吻合，适宜于描述植被覆盖的细节变化。

2.3 分析与预测

为定量评价NDVI非平稳时间序列模型的精度，在像元、区域级别年尺度上分别计算ANN-ARMA组合模型和非线性ANN模型的残差，结果如表2所示。

表2 像元、区域级别年尺度的2种模型残差

从表2可以看出，2种模型的估计值与NDVI原始值之间的差异并不显著。利用ANN-ARMA组合模型和非线性ANN模型，按照以下方法分别预测2011—2015年区域级别上的NDVI值：

(6)

表3 ANN与组合模型的精度检验

由表可以看出，ANN-ARMA组合模型的误差绝对值均小于0.001，比ANN模型误差小接近一个数量级，且ANN模型误差值域分布比组合模型更加离散，离差达到0.006 5，而组合模型离差仅有0.000 1。因此，相对于直接利用ANN建立的非线性模型，ANN-ARMA组合模型具有更好的预测精度，也能更加准确地描述NDVI3g数据的非平稳特征，有利于数据的建模与分析。

青海省的气候暖区主要分布在海拔2 000 m 以下的河湟谷地地区，次暖区主要分布在海拔3 000 m左右的柴达木盆地等地区，冷区主要分布在4 000 m以上的祁连山区和青南高原地区。考虑到2 000 m以下河湟谷地面积极小，将青海省划分为3 000 m以下、3 000～4 000 m和4 000 m以上3个高程带，利用ANN-ARMA组合模型对青海省2016—2025年各高程分区的植被覆盖变化进行预测，结果如图5所示。

从预测结果来看，2016—2025年青海省NDVI整体有上升趋势，3 000 m以下地区的NDVI值有降低趋势，3 000 m以上地区有上升趋势。而从近年来有关研究区植被覆盖变化的研究成果来分析，2000—2016年青藏高原植被覆盖改善的地区要比退化的地区面积大，其NDVI呈增加趋势[46]，与预测结果吻合，表明ANN-ARMA组合模型的预测结果可靠。

图5 各高程分区组合建模与预测

3 结束语

本文在对青海省GIMMS NDVI3g时间序列数据进行非平稳分析的基础上，利用人工神经网络模型研究了NDVI数据非平稳时间序列建模方法。基于1982—2015年的NDVI3g数据建立了青海省植被覆盖变化ANN非线性模型和ANN-ARMA组合模型，分析了模型精度，并预测了青海省2016—2025年的植被覆盖变化规律，主要结论如下：

①GIMMS NDVI3g时间序列数据具有显著的非平稳特性。

②ANN非线性模型和ANN-ARMA组合模型均能较好地模拟植被变化情况。组合模型较为光滑，能够凸显植被的总体变化趋势，而非线性ANN模型与观测值更为吻合，适宜于描述植被覆盖的细节变化。

③ANN-ARMA组合模型的精度高于ANN非线性模型精度。

④2016—2025年青海省植被覆盖整体有上升趋势，3 000 m以下地区植被覆盖有降低趋势，3 000 m以上地区有上升趋势。