基于LMD和GNN-Adaboost的滚动轴承故障严重程度识别

(北京卫星制造厂有限公司，北京 100090)

随着科学技术的迅猛发展，机械设备日益呈现出大型化、复杂化、智能化、集成化等特点。这些特点不仅使得更高的运行可靠性、安全性和经济性成为迫切的需求，同时也为设备的状态监测和维修管理提出了新的挑战[1-4]。滚动轴承(Rolling Bearing)作为机械领域应用最广泛的一种通用部件，在未来工业发展的历程中将继续扮演至关重要的角色，大型复杂机械设备长时间运行过程中，类似轴承这样的关键部件很容易出现磨损、疲劳、过载、腐蚀等现象，并进一步造成部件的局部损伤。任何一个细微的损伤都有可能影响机械设备的安全、稳定运行，甚至威胁到人们的生命与财产安全，因此研究能有效识别关键部件故障严重程度的方法具有重要的现实意义。

近几年，许多学者针对定量的基于知识的故障诊断方法进行了研究。这些研究内容大体可以分为两个主要的方面：一方面是，针对特定研究对象监测信号的特点，通过构建更加有效的信号处理方法来提取故障特征，如Wu，Costa等人提出的基于熵值的特征提取方法[5-6]，Tian等人提出的基于谱峭度(Spectral Kurtosis,SK)的特征提取方法[7]，以及时频域特征提取方法[8-9]；另一方面是，针对故障识别过程，利用各种模式识别方法来学习特征与故障模式之间的映射关系，从而实现自动化的故障识别。近几年许多模式识别方法被应用于故障诊断问题中，例如 k 近邻方法(k-Nearest Neighbor,KNN)、人工神经网络方法(Artificial Neural Network,ANN)、支持向量机(Support Vector Machine,SVM)等。Lei 等人根据每一个特征在识别过程中的有效程度不同，构建了基于特征加权 Euclidean 距离的KNN齿轮裂纹程度故障识别方法[10]。结合经验模态分解(Empirical Mode Decomposition,EMD)和局部均值分解(Local Mean Decomposition,LMD)等特征提取方法，KNN 也被应用于轴承的故障诊断问题中[11-12]。除 KNN 方法之外，ANN 也是一种被广泛应用于故障识别问题的方法，并且多种神经网络模型已经被应用于该问题中。多层感知机(Multilayer Perceptron,MLP)是最典型的一类前馈神经网络模型，通常利用后向传播(Back Propagation，BP) 算法来学习模型的参数。在构建故障识别模型的过程中，如何优化 MLP 模型的网络结构是一个重要的研究问题，现在故障诊断领域遗传算法(Genetic Algorithm,GA)[13]和粒子群优化算法(Particle Swarm Optimization,PSO)[14]已经被用来解决网络结构的优化问题。

本文针对不同工况下的轴承故障严重程度识别问题，提出了一种基于局部均值分解(Local Mean Decomposition,LMD)和遗传神经网络自适应增强(Genetic Neural Network Adaptive Boosting，GNN-Adaboost)的滚动轴承故障严重程度识别方法。 该方法合理结合了特征提取和模式识别方法的优点，可有效提高滚动轴承故障严重程度识别准确率。

1 滚动轴承振动机理及主要故障分析

1.1 滚动轴承振动机理

滚动轴承通过将运转中的轴座和轴之间的摩擦形式由滑动摩擦转变为滚动摩擦以减少由摩擦引起的机械设备损伤。滚动轴承的典型结构一般包括外圈、内圈、滚动体及保持架，如图1所示。

一般情况下，机械设备在运转过程中产生的振动主要由两个方面的原因共同作用引起：一方面是整体或局部不平衡状态、结构不对中、共振效应以及其他零

件等外部原因；另一方面是轴承结构特点、制造加工和安装等流程产生的误差，以及自身损伤故障等内部原因。通常情况下可以将滚动轴承的振动分为以下几类：

① 轴承结构引起的振动。这种振动是由轴承的固有性质引起的，与轴承是否异常没有直接关系。如由于轴承运转过程中，滚动体在不同位置受力程度不同引起轴颈中心偏移而产生的振动等。

② 加工精度引起的振动。这种振动是由加工精度引起的，当加工精度较低时，会引起轴承的振动。如轴承滚动体大小不同、接触表面粗糙程度不同等。

③ 轴承工作状态引起的振动。这种振动是由轴承运转过程中状态的改变而引起的，如由于加工和后期磨损引起的轴承偏心、轴承出现异常甚至故障情况等。

1.2 滚动轴承主要故障分析

轴承在长时间的运转过程中由于保养或使用不当等原因会产生不同部位、不同程度的损坏，即使在正常情况下，轴承工作一段时间后也会出现疲劳故障。常见的轴承故障类型有疲劳剥落、磨损、腐蚀、破损、压痕、胶合和保持架损坏等。滚动轴承在运转过程中，当轴承的各个零件经过故障损伤点时会因为相互撞击形成一系列的脉冲波，并具有一定的周期性，一般来说，把这种脉冲波称为冲击脉冲波，其产生的频率称为故障特征频率。滚动轴承主要的故障频率计算公式如下。

① 内圈故障特征频率。

(1)

② 外圈故障特征频率。

(2)

③ 滚动体故障特征频率。

(3)

④ 保持架故障特征频率。

(4)

式中，fr为内圈随轴旋转的频率;dm为轴承节圆直径;Dd为滚动体的直径;α为接触角;N为滚动体数量。

2 局部均值分解

轴承发生故障时，产生的周期性冲击信号具有调幅-调频特征，而 LMD方法可以将复杂的多分量调幅调频信号分解为单分量的调幅调频信号，且分解结果保持原信号的幅值与频率变化，因此LMD方法非常适合处理滚动轴承故障信号等非平稳非线性且多分量的振动信号[15-16]。

2.1 LMD算法

LMD方法将原始信号x(t)分解为PF分量与残余分量r(t)，其中PF分量由瞬时幅值与纯调频信号相乘得到，由纯调频信号又可求得信号的瞬时频率。忽略残余分量r(t)，原始信号x(t)可以表示为瞬时幅值与瞬时频率的函数S(f,t)，即

(5)

式中，ei(t)为第i个PF分量的瞬时幅值;fi(t)为第i个PF分量的瞬时频率;k为PF分量的个数。

对原始信号x(t)的分解过程如下：

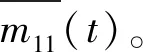
(6)

② 利用局部均值点，按式(7)计算相邻两个极值点aj和aj+1之间的包络估计值bj，将所有的bj连接后对折线进行平滑处理，得到包络估计函数b11(t)。

(7)

(8)

(9)

④ 如果s11(t)不是一个纯调频信号，即它的包络估计函数b12(t)不满足b12(t)=1，则将s11(t)作为原始信号x(t)，重复步骤①～步骤③，直到s1n(t)是一个纯调频信号，即-1≤s1n(t)≤1，它的包络估计函数b1(n+1)(t)满足b1(n+1)(t)=1，则有

(10)

(11)

⋮

(12)

式中：

(13)

(14)

⋮

(15)

迭代终止条件为

(16)

迭代分解过程在实际应用中是无法实现的，为了获得较为理想的纯调频信号，设定一个微小量Δ，当满足1-Δ≤b1n(t)≤1+Δ时，迭代终止。

⑤ 把迭代过程中产生的所有包络估计函数相乘便可以得到包络信号(瞬时幅值函数)：

(17)

⑥ 将包络信号b1(t)和纯调频信号s1n(t)相乘便可以得到原始信号的第 1 个PF分量，如式(18)所示。第一个分量包含了原始信号中最高的频率成分，PF1(t)的瞬时幅值即为包络信号b1(t)，瞬时频率f1(t)可由式(19)求出。

PF1(t)=b1(t)s1n(t)

(18)

(19)

⑦ 将PF1(t)从原始信号中分离出来，得到新的信号u1(t)。

u1(t)=x(t)-PF1(t)

(20)

⑧ 将u1(t)作为原始信号x(t)重复步骤①～步骤⑦，循环k次，直到uk(t)为一个单调函数为止。

u1(t)=x(t)-PF1(t)

(21)

u2(t)=u1(t)-PF2(t)

(22)

⋮

uk(t)=uk-1(t)-PFk(t)

(23)

原始信号x(t)被分解为k个PF分量和一个单调函数uk(t)之和，即

(24)

2.2 提取PF能量矩

通过LMD方法将原始信号x(t)分解为k个PF分量和一个单调函数uk(t)之和，将瞬时幅值bp(t)和瞬时频率fp(t)带入式(5)，原始信号x(t)可以表示为瞬时幅值与瞬时频率的函数S(f,t)，即

(25)

根据原始信号x(t)的时频分布表示形式，可以计算信号在时频空间的局部能量，即

(26)

由于PF能量矩在考虑能量大小的同时也考虑到能量大小随时间的分布情况，与仅计算能量值相比，PF能量矩能更好地揭示能量在时间轴上的分布统计特性，因此可以将能量矩作为反映滚动轴承故障特征参数的一部分，进而提高模式识别等方法对滚动轴承的故障类型和故障程度进行分类识别的能力。

3 GNN-Adaboost算法

3.1 遗传神经网络(GNN)

遗传神经网络(GNN)结合了遗传算法较强的搜索能力和神经网络较强能实现非线性映射等特点，在故障辨识领域应用广泛。

遗传算法GA(Genetic Algorithm)通过模拟生物进化过程中遗传选择的理论建立数学模型，根据遗传学中染色体复制、交叉、变异等过程，设计出了一系列遗传算子，遗传算子作为遗传算法的操作基础，对遗传算法的性能起着决定性作用[17-19]。

遗传算法的基本流程如下。

① 编码。对可行域内的点依次进行编码。常见的编码方式有实数编码、0/1编码等。经过编码的数据或样本被称为个体，随机从个体集合中选取一部分个体，组成初始种群，作为遗传进化的第一代。

② 复制、交叉和变异。从种群中随机选取部分个体，并对其进行复制、交叉和变异操作。常见的交叉方式为单点交叉和多点交叉，常见的变异方式为单点变异和多点变异。交叉和变异操作会产生新的个体，使种群多样性增加，提高了更优解出现的概率，防止算法陷入局部最优。

③ 选择。对种群中的个体计算适应度作为寻优信息，从种群中选择适应度高的个体保留下来，淘汰适应度低的个体，更新种群。

④ 迭代。重复步骤①～步骤③，直至算法收敛。

遗传算法流程图如图2所示。

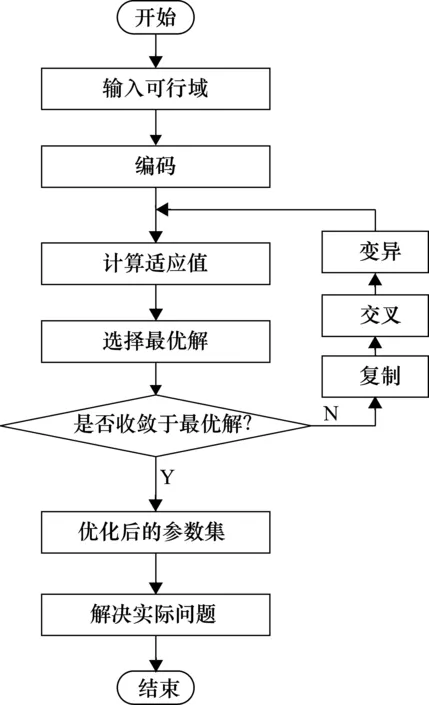
图2 遗传算法流程图

GNN是一种利用GA算法优化神经网络的智能算法，GNN的基本步骤如下：

① 样本输入。将从原始信号中提取的特征参数作为GNN网络的输入。

② 网络训练。设定神经网络的结构、权值、适应度函数等，将样本输入设计好的网络中，对比网络的实际输出与期望输出，直到两者误差满足精度要求即可停止训练，得到训练好的网络。若误差不满足精度要求，则修改网络权值重复训练，直到满足精度要求为止。

③ 样本测试。选取未经过训练的样本作为测试样本 ，输入到步骤②中已经训练好的网络中，得出判断结果，并对结果进行分析。

GNN流程图如图3所示。

3.2 Adaboost算法

Adaboost (Adaptive Boosting)是由Yoav Freund和Robert Schapire在1995年提出的一种将多个弱分类器组合成强分类器的自适应增强方法。其自适应在于，该算法可以对前一个弱分类器分错的样本增强其对应的权值，权值更新后的样本被用来训练下一个新的弱分类器[20-21]。在每次训练中，都用样本总体训练新的弱分类器，并产生新的样本权值以及该弱分类器的话语权，一直迭代直到达到最大迭代次数或预设的错误率。

对于训练集A={(x1;y1)…,(xq;yq)…,(xD;yD)},yq∈Y={1,2,…,K}，其中D为样本总数，设迭代最大次数为T，则算法流程如下：

图3 GNN算法流程图

① 初始化训练数据的权值。对每一个训练样本，初始化时赋予同样的权值W=1/D，设第i次迭代训练集的权值集合为Wi={wi1,wi2,…,wiq,…,wiD},i≤T,wiq为第i次迭代时的第q个样本的权值。当i=1时，wiq=1/D，q=1,2,…,D。

② 对每个特征f，用具有权值分布Wi的训练样本集训练弱分类器Gf,i(x,f,θ,δ)，计算弱分类器的加权错误率εf,i为

(27)

式中,θ为弱分类器的阈值;δ为弱分类器的偏差参数。

③ 按最小错误率选取最佳弱分类器Gi(x)。

(28)

④ 按最佳分类器调整权重。

(29)

式中，βi=εi/(1-εi)为更新因子;eq为分类检测变量，当样本xq被分类正确时，eq=0，否则eq=1。

⑤ 重复步骤①～步骤④，直到i=T，则最后的强分类器为

(30)

3.3 GNN-Adaboost算法

GNN-Adaboost算法将GNN作为Adaboost算法的弱分类器，可以高效地解决分类问题。GNN-Adaboost算法的具体步骤如下：

① 样本预处理与网络初始化。从样本空间中随机选择D组样本作为训练集A，按3.2节中的步骤①初始化样本权值Wi；确定GNN的结构和阈值。

③ 确定弱分类器的权重。根据各个GNN的预测效果，即εi，计算各个GNN弱分类器的权重αi。

GNN-Adaboost算法流程图如图4所示。

图4 GNN-Adaboost算法流程图

4 故障严重度识别方法及算例分析

4.1 滚动轴承故障严重度识别方法

本文基于LMD方法与GNN-Adaboost算法，提出了一种针对滚动轴承的故障严重程度识别方法。对滚动轴承原始信号进行局部均值分解，得到各个PF分量，并计算PF能量矩，结合原始信号的时域特征值，包括方差、偏度、峭度，组成滚动轴承振动信号的特征参数。将特征参数作为GNN-Adaboost算法的输入样本，进行训练与测试，具体流程如图5所示。

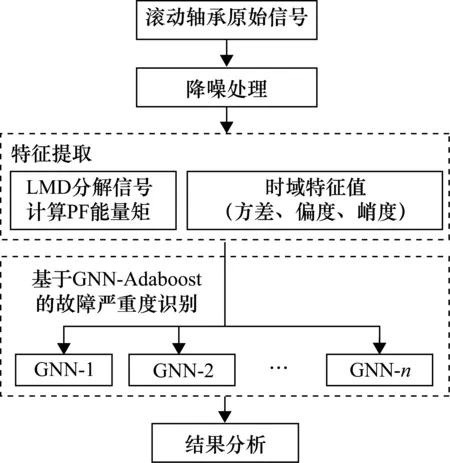
图5 基于LMD和GNN-Adaboost的轴承故障程度识别流程图

4.2 数据描述

数据集A、B、C均取自西储大学(CWRU)的滚动轴承故障诊断数据集[22]，如表1所示。测试轴承型号为6205-2RS SKF的深沟球轴承，将振动加速度传感器固定于轴承上方，采集正常、内圈故障、外圈故障和滚动体故障的振动信号，且每种故障类型包含3个故障程度，即损伤直径分别为0.178 mm,0.356 mm,0.533 mm，采样频率为12000 Hz。A、B、C三组数据对应的测试负载分别为0hp，1hp，2hp(0 kW，0.7355 kW，1.4710 kW)，对应的转速分别为1797 r/min，1772 r/min，1750 r/min，1730 r/min。

表1 数据集A/B/C/D详细信息

4.3 基于LMD的能量矩提取

对4.2节中的A、B、C三组数据进行基于LMD的能量矩提取。以工况0hp下的正常轴承为例，其LMD分解结果如图6所示。图7为分解所得的6个PF分量对应的能量柱状图，由图可知能量主要集中在前5个PF分量中，因此在后续的轴承振动信号PF分量能量矩提取过程中均选择前5个PF分量。

图7 正常轴承信号在0hp工况下的PF能量矩

当载荷为1hp时，各级损伤程度对PF分量能量矩的影响如表2所示，通过对270组数据的测试与分析发现，不同故障类型在同一损伤程度下，外圈故障的第一阶PF分量的能量最大，内圈故障其次，滚动体故障最小。此外，根据式(1)～式(3)可计算实验轴承的内圈故障特征频率、外圈故障特征频率、滚动体故障特征频率分别为162.19 Hz，107.36 Hz ，141.17 Hz，而各类故障信号的PF分量中PF4分量对应的频率最接近各故障特征频率，分别为161.90 Hz，106.84 Hz，142.3 Hz，且由表2可知，随着损伤程度的增加，内圈故障和外圈故障的PF4分量的能量均先减小后增加，而滚动体故障的PF4分量的能量先增加后减少，说明滚动轴承振动信经过LMD分解后的PF分量能量矩可以作为表征轴承故障类型和故障程度的特征参数。

表2 损伤程度对PF分量能量矩的影响

4.4 基于能量矩和时域特征的故障程度识别

提取滚动轴承原始信号的时域特征，并与4.3节中的PF能量矩组合，形成包含8个分量的特征参数组，如表3所示。

表3 基于PF能量矩与时域特征的滚动轴承特征参数组

以表3所示的滚动轴承特征参数组作为GNN-Adaboost算法的输入，以表1所示的数据标签作为GNN-Adaboost算法的分类依据。本文所有算法和程序均用Matlab R2018a编程软件实现，运行环境为Windows10专业版，Intel Core i5-8400 CPU @ 2.80GHz,16GB RAM。为了保证本文所提出的方法的合理性，从A、B、C三个数据集中，分别随机选取各个载荷条件和损伤程度条件下的样本中的70%作为训练集，其余30%作为测试集。为了验证本文所提出的方法的有效性，将本文所提方法的故障严重度识别准确率与其他方法的识别准确率进行对比，对比结果如表4所示，其中SVM表示支持向量机。

由表4可知，本文所提出的基于LMD和GNN-Adaboost算法的轴承故障严重度识别方法与基于EMD或基于GNN算法、SVM的方法相比，准确率更高，说明本文所提的方法能更合理地提取反映轴承故障类型和故障严重程度的特征参数，且能更有效、更准确地对所提取的特征参数进行分类。

5 结束语

本文针对滚动轴承故障严重度识别问题，分析了滚动轴承的振动机理和主要的故障类型，针对常见的故障类型，即内圈故障、外圈故障和滚动体故障，设计了基于LMD和GNN-Adaboost算法的故障严重度识别方法。基于LMD的轴承信号分解方法有效地将滚动轴承的振动信号分解为多个具有瞬时频率意义的分量PF，通过分析这些PF分量的能量分布情况及其所包含的频率值发现，不同故障类型的PF分量能量不同，外圈故障的第一阶PF分量能量最高，内圈其次，滚动体的第一阶PF分量能量最低。同时，考虑到3种不同故障类型的故障频率，经过分析发现第4阶PF分量的瞬时频率最接近故障频率，且随着故障程度的加深，内圈故障和外圈故障的PF4分量的能量均先减小后增加，而滚动体故障的PF4分量的能量先增加后减少，说明PF分量的能量分布可以有效地表征轴承的故障类型和故障程度。通过整合轴承信号的PF分量能量矩和原始信号的时域特征值，得到了包含8个分量的特征参数组，并以该特征参数组作为GNN-Adaboost算法的输入，实现对轴承故障类型和故障程度的分类。经过训练与测试，并与其他方法对比发现，基于LMD和GNN-Adaboost算法的滚动轴承故障程度识别方法具有更高的识别准确率。

表4 不同工况下不同方法的滚动轴承故障严重度识别准确率

当然，目前对于滚动轴承故障特征提取的方法仍然有待提高，根据实验结果可以发现，经过LMD分解后的故障特征频率分量所占的能量比较低，今后的研究重点将放在如何强化故障频率对信号分解结果的影响，以更好地提高分类算法对故障严重程度的敏感度。