下肢康复外骨骼机器人模糊PID控制研究与仿真

(东华大学 机械工程学院，上海 201620)

随着社会老龄化的加剧和人民生活水平的提高，由脑卒中、脊髓损伤、脑外伤等原因造成的残障人口迅速增长[1]。同时，各类肢体残疾患者需要医疗康复和辅助设备，然而国内现在资源不足，相关产业人员严重不足。康复外骨骼机器人不仅可以为肢体力量较弱的患者提供个性化的训练方案，帮助他们进行康复训练改善运动功能障碍，还可以减轻治疗师负担、节约社会资源[2]。

设计的下肢康复外骨骼机器人属于被动式运动控制，它所起的作用是辅助使用者行走或者进行康复训练。将人体步态特征分解为单独的部分，然后将其运动规律和驱动信息提前存入电机中，人在行走时发出指定信号，控制系统接收到信号进行分析后驱动电机进行相应的动作[3]。

相比于传统的工业机器人，下肢康复外骨骼机器人是一个多输入多输出机构，其不确定性和非线性都很高，因此对电机的控制能力提出了很高的要求。目前已有许多机构与研究所制造出了样机，如加州大学伯克利分校Kazerooni教授带领的团队在2010年推出的医用外骨骼Ekso，Ekso通过采集患者当前的运动趋势进而控制外骨骼的运动，并可以通过背部的控制器手动调节运动状态[4]；韩国首尔HEXAR公司为脑卒中后偏瘫患者开发的WA-H利用检测行走时其质心的变化，进而调节电机进行平衡控制[5]；日本筑波大学研发的HAL-5,通过接收人体的肌电信号来分析穿戴者的运动意图进而驱动电机运动；美国Argo Medical Technologies公司开发的ReWalk利用倾角传感器来获得穿戴者的运动状态从而调整电机输出。

但是不管采用哪种交互方式，都需要对外界输入信号进行判断并得到恰当的输出。经典PID控制结构简单且被广泛使用，但是经典PID控制也存在着一些问题。因此有人在经典PID的基础上进来了改进，比如方醉敏[6]等人提出的基于专家控制规则的PID控制结构克服了经典PID结构中被控对象具有非线性、时变、大纯滞后等特性；孙悦[7]等人提出了改进蚁群算法的PID参数优化方法，通过结合蚁群算法和PID技术，对PID参数进行优化，取得了较好的控制效果。但这些控制结构中其参数固定，而下肢外骨骼康复机器人需要适应不同的人群、不同的穿戴条件，所以系统参数会发生变化，这些控制算法已经不能很好地满足要求。而对诸如神经网络、滑模控制、模糊控制等智能算法进行对比后，由于模糊控制结构清晰，能够适用于各种复杂非线性问题，能够动态改变系统参数，所以选取其与经典PID一起构成模糊PID控制来实现下肢康复外骨骼机器人的运动。

构造了下肢康复外骨骼机器人的动力学模型，设计了一种开关切换式模糊PID控制方法对其进行控制。联合ADAMS与Matlab/Simulink 软件进行仿真分析对比，验证所设计方法的合理性。由于采用了开关切换式模糊PID，其中模糊PID的参数可以根据穿戴者情况的不同进行调节。因此本文在建模、仿真和分析的过程中未将不同佩戴者的这一因素放入其中。

1 下肢康复机器人模型

1.1 ADAMS模型建立

ADAMS具有很强大的动力学分析功能，但是并不擅长构建较为复杂的虚拟样机模型，而下肢康复外骨骼机器人较为复杂，因此先在SolidWorks中建立其三维模型，如图1所示，主要由腰部模块、大腿模块、小腿模块、足部模块及髋、膝、踝三个关节组成。将其三维模型保存为*.x_t格式，通过模型数据接口导入到ADAMS软件中，设置材料为铝合金和各个部位的参数。驱动电机的最大扭矩为100 N·m，最大功率为500 W。模型具体参数如表1所示。

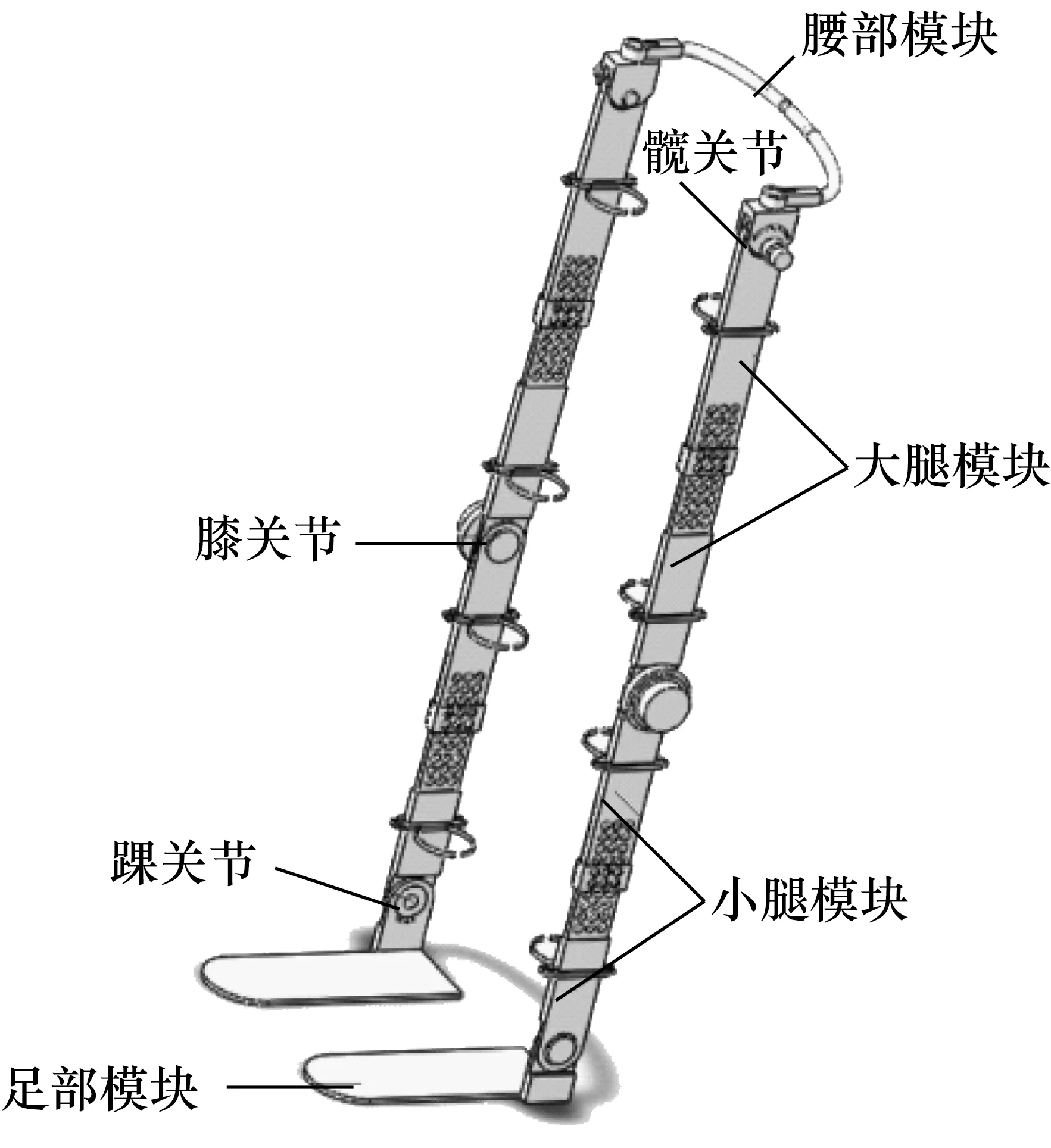
图1 SolidWorks中的外骨骼机器人模型

表1 外骨骼模型惯性参数

在ADAMS中对模型进行必要的约束。由于下肢康复外骨骼机器人主要运动是在矢状面内，所以忽略模型在运动时的侧向摆动。在下肢髋、膝、踝关节处各设置一个转动副，同时添加足部与地面直接的接触力[4](碰撞接触，刚度100 N/mm，力指数2.2，阻尼10 N·s/mm，穿透深度0.001 mm)，保证模型在地面上行走而不会下陷。添加髋部与地面的水平约束，保证髋部只相对于地面平动。在左右髋、膝、踝关节处添加驱动(motion)。完成配置后的模型如图2所示。

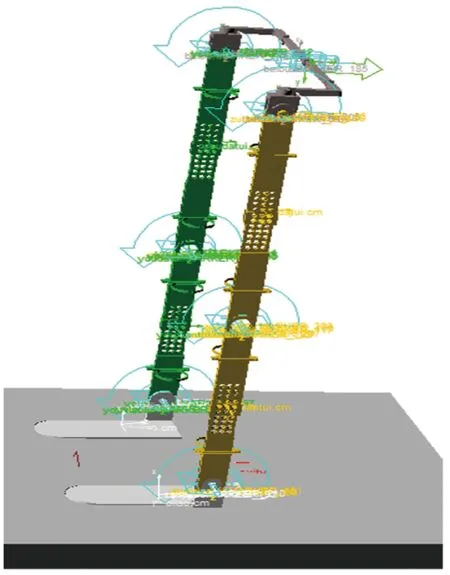
图2 ADAMS中配置好的模型

1.2 动力学分析

人体正常行走时下肢可以分为支撑相和摆动相。支撑相指足部接触地面和承受重力的时间，约占整个周期时长的62%；摆动相指足部离开地面向前迈步到再次落地之间的时间，约占整个周期时长的38%[5]。本文模型以支撑相为基准，建立动力学模型。

如图3所示，选定坐标系O0为基准坐标系，固定在外骨骼背部中心处，坐标系O1位于髋关节位置并固定在大腿连杆上，坐标系O2位于膝关节位置并固定在小腿连杆上，坐标系O3位于踝关节位置并固定在足部。

图3 单侧腿单腿支撑模型

图中m1、m2和m3分别为大腿连杆、小腿连杆和踝关节以下连杆的质量；d0、l0为踝关节距离腰部中心点的距离；d1、d2和d3为各连杆的质心距相应关节的距离；l1、l2和l3分别为外骨骼大腿、小腿和脚的长度；θ1、θ2、θ3为髋关节、膝关节、踝关节的转动角度；T1、T2、T3则为对应关节的扭矩。所以，系统的整体动能和势能为

(1)

(2)

则，系统的拉格朗日方程为

L=EK-EP

(3)

(4)

由式(1)～式(4)，然后将力矩用各连杆间角度进行表示，可以得到各关节的驱动力矩：

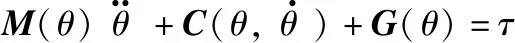
(5)

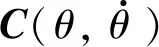
2 控制系统的设计

经典PID控制具有结构简单、应用灵活等特点。由比例(proportion)、积分(integral)、微分(derivative)三部分组成[6]，其传递函数为

(6)

式中，Kp为比例增益；Ki为积分增益；Kd为微分增益。

在这里选用经典PID模型而不是微分先行、增量式、控制死区等，是基于以下几点考虑的：

① 微分先行PID控制只对输出量进行微分，而对给定指令不起微分作用，它适用于给定指令频繁升降的场合，可以避免指令的改变导致超调过大，但是它会导致响应速度变慢。而外骨骼机器人的输入驱动信息都是平滑的曲线，很少出现大幅度的跳跃，且步态角度误差e也不是很大，为了加快响应速度，所以没有使用微分先行PID控制。

② 增量式PID控制算法是一种递推算法，输出控制量增量，并无积分作用。而本外骨骼机器人需要连续改变机构位置，时刻适应人体姿态，就需要对之前的累积误差进行消除，所以并不适用。

③ 带死区的PID控制则是在经典PID中引入了死区的概念。当偏差小于设定之后便认为没有误差不进行调节。但是在零点附近时，若偏差较小，进入死区后偏差变为“0”会导致积分消失，此时如果系统依然有静态误差则不能消除，需要人为处理。而本外骨骼机器人需要精确的控制，如果增加死区，太小的话起不到明显作用反而增大了计算量，而设置偏大则会令输出曲线无法紧随输入曲线，导致跟随效果变差。

模糊控制(Fuzzy Control)是一种由模糊集理论、模糊控制逻辑和模糊语言变量为基础组成的智能控制方法[7]。它能够模仿人脑思维来对一些不方便建立数学模型的系统进行控制。模糊控制系统主要由4个部分组成：模糊化接口、推理机、知识库和反模糊化接口[7]。

① 模糊化接口。模糊控制器并不是什么信号都可以识别的，在进行模糊推理之前，需要将输入信号转化为推理机可以识别的模糊量，模糊化接口就是完成这部分工作。转化后的模糊量用模糊子集来表示。

② 推理机。根据规则库的条件，将模糊化的输入变量变为输出变量的结构。

③ 知识库。包含规则库和数据库两个部分。数据库存有所有的输入、输出变量的全部模糊子集的信息；而规则库则是模糊控制的一个核心，如何根据不同输入量得出适当的输出量，这取决于一个规格库设计的是否合理。规则库通常使用if…is…and…is…then…is…的形式来编写。

④ 反模糊接口。模糊化的输入变量经过推理机后，得到的仍是模糊化的输出变量，不能直接被控制器所识别，需要将其变为精确量。反模糊接口通常使用最大隶属度法、重心法、加权平均法等方法来进行反模糊处理。

2.1 模糊PID控制器设计

由于下肢康复机器人具有非线性和强耦合性，所以参数固定的经典PID控制器无法满足精确控制的要求，但是通过模糊控制器自整定参数后可以解决这一问题。

PID参数Kp、Ki、Kd的自整定公式如下：

(7)

式中，Kp(0)、Ki(0)、Kd(0)为PID控制器初始值，ΔKp、ΔKi、ΔKd为模糊控制器的自整定输出量。

2.1.1 确定模糊控制器结构

在此综合控制器中，模糊控制器的主要作用是根据输入变量，即关节步态角度误差e及其微分ec，不断整定PID控制器的参数Kp、Ki、Kd，得到输出变量ΔKp、ΔKi、ΔKd，因此采用二输入三输出的形式。将输入变量与输出变量的模糊集均设定为7挡的{NB(负大)、NM(负中)、NS(负小)、ZO(零)、PS(正小)、PM(正中)、PB(正大)}[8]格式。这样挡极多，规则制定灵活、细致，可以适应不同条件下的控制。同时将输入、输出变量量化到(-3,3)区域，论域为{-3，-2，-1,0,1,2,3}。

2.1.2 确定输入输出变量的隶属度函数

因为需要较高的分辨率与灵敏度，因此选用隶属函数形状较尖的三角形隶属函数，能对误差做出快速反应，适合在线整定参数的模糊PID控制[9]。

2.1.3 建立模糊控制规则

模糊PID控制器的重中之重就是模糊规则的制定，规则的好坏决定了控制器能否准确、快速地对输入量进行正确的识别与输出。控制器根据关节步态角度误差e及其微分ec作为输入来对PID控制器的参数进行自整定调整，因此，可以利用PID参数的配置经验[10-13]：

① 当输入误差|e|较大时，为了使控制系统迅速地响应，应设置较大的Kp。同时为了避免因e的突然变化导致微分过饱和，设置较小的Kd值。最后令Ki=0保证系统不会产生较大的超调，发生积分饱和现象。

② 当输入误差|e|处于中等大小时，适当减小Kp的值来保证超调量处于合适的范围。此时微分会对系统产生较大影响，应取适中的值保证系统的响应速度。

③ 当输入误差|e|接近设置值时，可以适当增大Kp和Ki的取值来保证系统的稳定性。同时，根据ec的值来设定Kd的值。ec较大时，Kd取较大值；ec较小时，Kd取较小值。

基于以上经验，初步配制出Kp、Ki、Kd的模糊控制规则，如表2所示。

表2 Kp、Ki、Kd的模糊规则

2.1.4 去模糊化

关节步态角度误差e及其微分ec经过推理机推理后，得到模糊输出值U。U是一个模糊子集，需要通过去模糊化才能变成精确控制量u。目前常用的方法有加权平均法、最大隶属度法和重心法。本文使用工业控制中广泛应用的加权平均法来进行去模糊处理[10]。输出值由式(8)决定：

(8)

式中，μ(y)为元素y对所属模糊集的隶属度。

2.2 开关切换式模糊PID控制器

虽然模糊PID控制器可以自整定PID参数，有很强的适应性，但是模糊规则较多，且系统中不只有一块模糊PID控制器，整体模糊计算量非常大，会影响计算速度，造成反应速度变慢。经典PID控制器结构简单，计算量小，所以将二者结合起来，取长补短。

因此开关切换式模糊PID控制器比单纯的模糊PID控制器响应速度更快，比单纯的经典PID控制器精度更好，稳定性更好，整体震荡和超调都较小。其控制系统结构示意图如图4所示。它可以根据输入变量|e|的大小灵活使用不同控制方法。输入变量|e|是期望数值与跟随数值的差值，它的大小决定了驱动电机的输出功率的大小同时也能够反映出输入与输出信号之间是否有大的数值跳跃，所以选取其作为切换的条件。当输入变量|e|大于设定值时，控制器采用模糊PID控制器来对参数进行自整定，使输出结果更加精确。反之则使用经典PID控制，节省大量的时间，保证整体控制具有良好的响应速度。

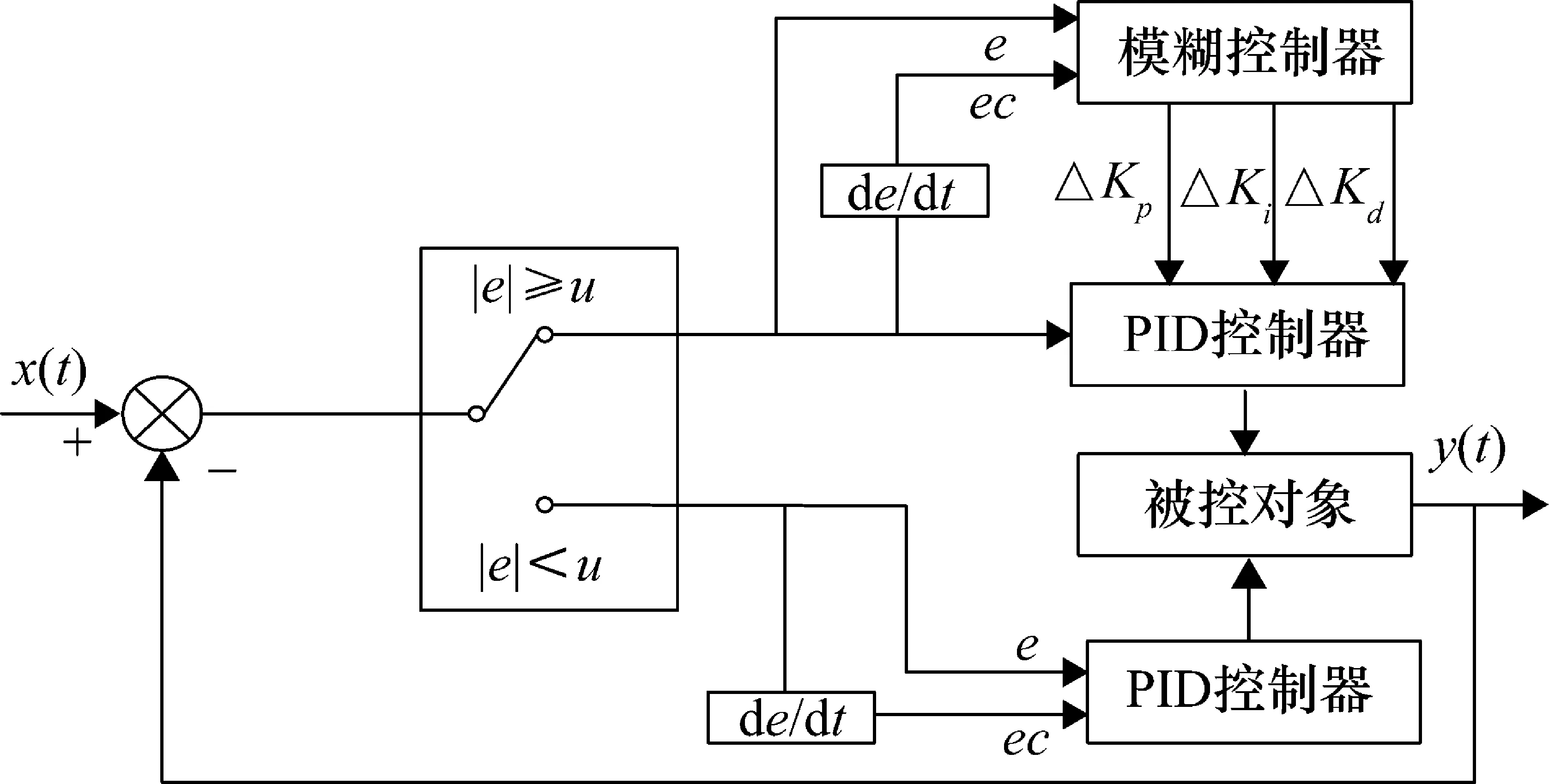
图4 开关切换式模糊PID控制系统结构示意图

3 仿真及分析

前文已对模型进行了动力学分析，同时设计了开关式模糊PID控制器，所以基于ADAMS与Matlab进行联合仿真分析。

根据动力学分析，然后采用负反馈控制，下肢外骨骼康复机器人控制模型的传递函数为[14]

(9)

由于不同的关节步态特征不同，需要采用不同的传递函数来单独驱动。本文以髋关节为例进行仿真分析。根据模型参数，可以得到a=5，b=5，k=100。如图5所示，在Simulink中完成各种控制器模型的搭建。“PID control”模块即为经典PID控制器，“fuzzy control”模块为模糊控制器，两者联合组成“fuzzy-PID”模糊PID控制器。结果是由模糊PID控制器产生还是经典PID控制器产生取决于阈值|u|的选择。

图5 开关切换式模糊PID控制器仿真模型

根据式(5)计算出个关节所需驱动后，代入图6中。图6中 Sub模块即为封装好后的开关切换式模糊PID控制器;Adams_sub模块为ADAMS模型在Simulink中的动力学控制模块。输入各关节的驱动信息，经过不同参数的控制器后，ADAMS接收到信号然后产生相应的运动，最后将关节角度信息返回到Simulink中。模型运动图如图7所示。以髋关节为例，下肢康复外骨骼机器人模型关节的理论运动轨迹与经过不同控制器后的实际运动轨迹图及其误差图如图8所示。

由于理论轨迹不是从0°开始的，所以不论是经典PID控制器还是模糊PID控制器都有一个从0°逼近理论值的过程。由图8(b)可知，经典PID与模糊PID控制器经过很短的时间后都可以较好地跟随目标曲线，但是经典PID控制器跟随时超调量在3°左右，而且逼近目标曲线后仍有1°～2°的误差，而模糊PID控制器超调量很小，在0.5°左右，其后的跟随过程波动幅值很低，基本与目标曲线重合，具有很好的控制效果。同时根据图8(b)可以看出模糊PID控制的跟随曲线稳定所需的时间约占总时长的15%，而经典PID控制的跟随曲线稳定所需的时间约占总时长的30%。由此说明模糊PID控制具有良好的精度且响应速度较快。

将模糊PID控制器与经典控制器通过开关组合起来，形成开关式模糊PID控制器，具体模型如图7所示。同样的条件进行仿真后，将结果与模糊PID控制器进行对比，得到结果如图9所示。

图6 ADAMS与Simulink联合仿真图

图7 模型仿真运动图

图8 控制精度比较

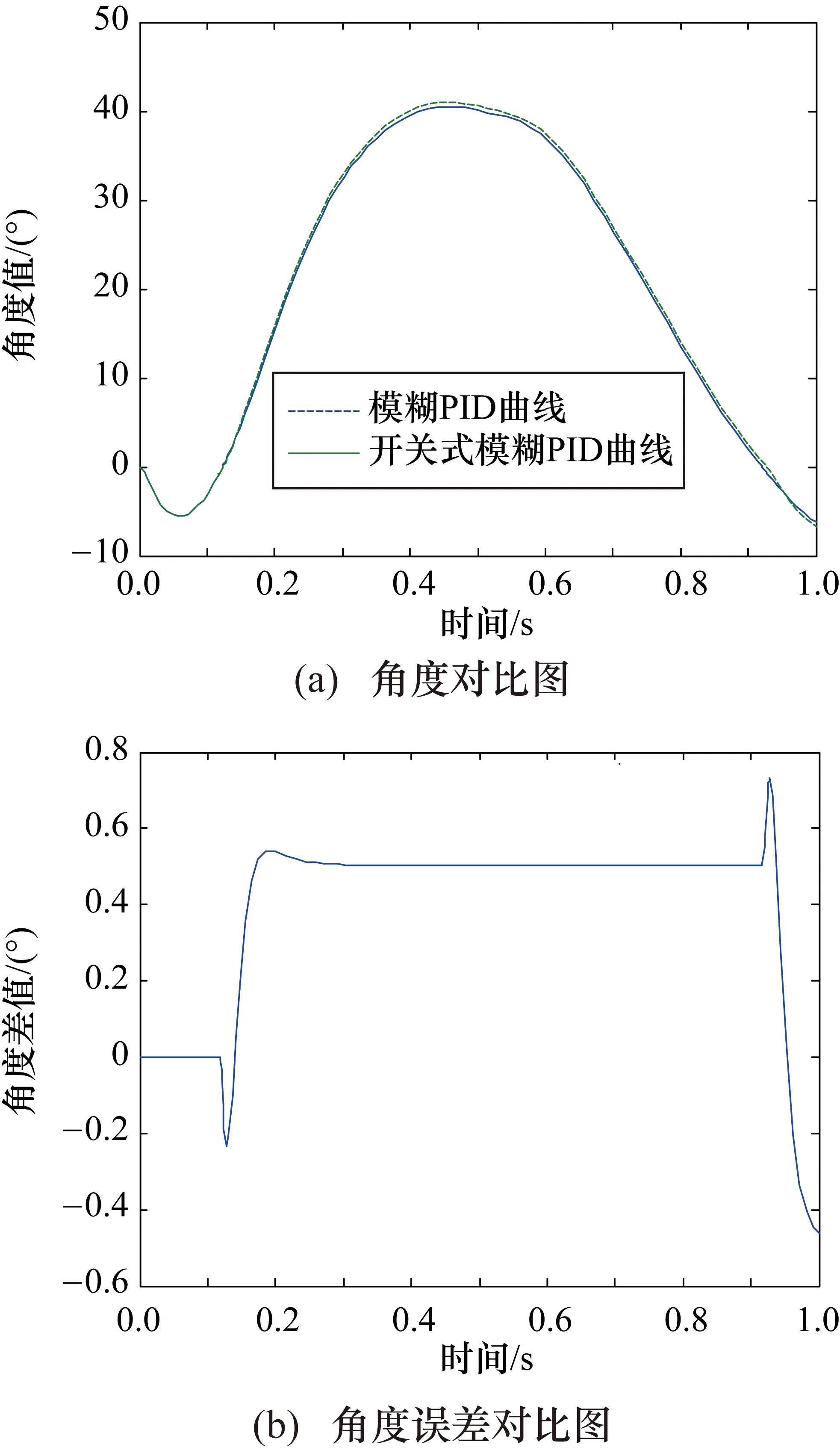
图9 模糊PID与开关式模糊PID对比图

从图9可以看出，开关式模糊PID控制器跟随曲线与模糊PID控制器的跟随曲线趋势一致，幅值大小也基本一致，误差保持在0.6°以内，能够很好地完成模糊PID所完成的工作，但是所需的计算量会减少很多。

4 结束语

采用了开关切换式模糊PID控制器来对下肢康复外骨骼机器人进行运动控制研究。为了更好的验证控制效果，对外骨骼机器人进行了三维建模和动力学分析，并将其导入仿真分析软件ADAMS中，与Matlab/Simulink进行联合仿真。仿真过程中代入模型动力学分析后的力矩驱动信息，开关式模糊PID控制器控制模型运动获得跟随曲线。通过跟随曲线与目标曲线的对比分析，可以看出开关式模糊PID控制器比传统PID经典控制超调量更小，角度变化更加精确，与模糊PID控制器相比，在计算量更小的前提下，控制精度相似，能够保证穿戴者与下肢康复外骨骼机器人运动协调一致。