基于改进MPSO-SVM 算法的下肢连续运动预测模型
隋修武,石 峰
(天津工业大学 机械工程学院,天津 300387)
康复训练机器人具有比人工医疗师辅助训练更多的优点而被研究者和康复工作者所认可,目前世界上典型的下肢康复训练机器人有LOPES、LOKOMAT、Gait Trainer 和Haptic Walker 等[1]。康复训练过程一般分为被动阶段和主动阶段,主动阶段期间实现康复机器人与人本体之间的人机交互,尤其是康复机器人与人体自身运动的协调是康复机器人运动规划与控制要解决的关键问题之一[2]。传统的人机交互多通过力、位置传感器等进行人体运动意图预测而实现。利用力、位置传感器不仅会使操作者感觉累赘,还会由于人体运动与反映意图的神经冲动之间存在自然的电-机延时现象,从而导致人体运动意图的预测不可避免的存在滞后,最终只能实现人体意图的康复机器人部分闭环控制或不稳定控制[3]。近年来基于表征肌肉活动的无创的表面肌电信号预测人体运动意图也因此成为实现人机自然交互的一种重要接口形式[4]。
利用模式识别技术,通过人体表面肌电信号对人体运动意图进行模式识别,并基于模式识别的结果控制康复机器人按照某种运动轨迹进行运动,已成为目前学术研究最为成熟的方向之一[5]。但现有康复机器人多数是直接利用模式识别结果只作为开关信号,因此机器人的运动也是刻板、不自然、不人性化的。近年来,以围绕着获取更加自然的人体运动意图,实现基于表面肌电信号的连续运动预测为目的的研究成为热点之一。Dario Farina 团队针对腕关节1~2 个自由度的连续运动估计开展了广泛的研究,部分研究成果被成功地应用于德国Otto bock 假肢手腕关节的肌电控制[6]。该团队主要采用线性回归、神经网络或非负矩阵分解等方法进行肌电-运动映射关系的训练。文献[7-10]分别针对上肢肩/肘关节、手指关节的连续运动预测,采用人工神经网络、卡尔曼滤波、高斯过程回归等训练方法从肌电信号解码出关节角度信息。基于肌电信号的人机接口在人体下肢运动意图识别方面的研究远远落后于上肢运动意图识别,尤其在连续运动预测方面。
针对当前下肢连续运动预测精度低的问题,本实验提出一种基于改进的MPSO-SVM 算法对下肢连续运动预测模型进行建模的方法。即引进指数函数和正弦函数对PSO 算法的惯性因子ω 进行优化,使用改进后的MPSO 算法对SVM 算法的参数进行最优化处理,并建立连续运动预测模型。最终通过实验的方式对该算法进行有效验证。
1 基本原理和方法
1.1 支持向量机原理
支持向量机(SVM)是1995 年首次提出的一种分类技术[11],用于模式识别和非线性回归。其主要思想是将低位向量映射到高维空间,在高维空间找出输入量与输出量之间的映射关系。
SVM 的最优权值向量ω*和最优偏置b*为

式中:αi*为支持向量,αi*=[α1*,α2*,…,αM*]T,αi*> 0,i=1,2,…,M,M < N。
选择径向基核函数(radial basis function,RBF),RBF 核函数为:

相应于核函数将之前的分类函数映射成
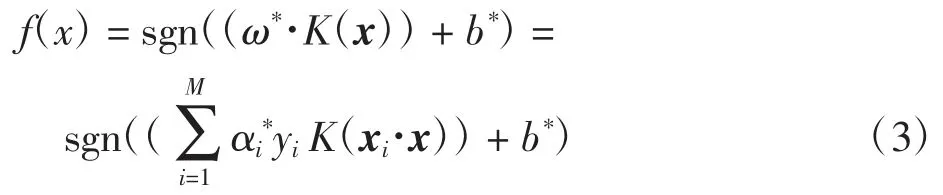
式中:xi为支持向量机;x 为未知的输入向量;K(xi,x)=K(xi)·K(x)。
1.2 粒子群优化算法
粒子群优化算法(PSO)将所要寻优问题的每个解都称为一个粒子,设由n 个粒子组成的群体对Q 维(每个粒子的维数)空间进行搜索,每个粒子i 对应的位置记为 xi=[xi1,xi2,…,xiQ]T,每个粒子 i 对应的速度记为 vi=[vi1,vi2,…,viQ]T,当前每个粒子 i 搜索到的历史最优位置记为 Pi=[pi1,pi2,…,piQ]T,当前全部粒子搜寻到的全局最优位置记为 Pg=[pg1,pg2,…,pgQ]T[12]。
粒子的速度和位置的更新方程为:

1.3 粒子群算法参数优化
惯性因子ω 的大小对算法的收敛速度和寻优精度起着关键性作用[13]。根据粒子适应度值的大小将粒子进行等级划分,对每个等级的粒子采用不同策略进行惯性因子调整,是每个粒子都能根据各自的适应度值选择合适的惯性因子ω,从而使粒子收敛到全局最优位置。为提高算法运行效率,将粒子分为2 个等级。
对每次进化中所有粒子的惯性因子ω 采取自适应调整,具体步骤为:
(1)计算该种群中所有粒子的适应度值的平均值favg,种群中有n 个粒子,记该种群第i 个粒子的适应度值大小为fi,则

(2)适应度值大于favg的粒子,由于它们更加接近最优解(C,σ),惯性因子ω 应设置很小的值。若惯性因子ω 为固定值,算法很容易陷入局部优化,很难达到全局寻优效果。为克服上述缺点,本文提出一种基于指数函数递减的方式,以保证种群在搜索初期保持较大的速度进行,在搜索中让搜索速度快速下降,使粒子更容易收敛到全局最优。

式中:k=1,2,…,A;A 为最大迭代次数;ω(k)为第 k 个粒子的惯性因子;ωstart和ωend分别为设置的最大的惯性因子和最小的惯性因子。一般ωstart=0.9;ωend=0.4。
(3)小于等于favg的粒子,它们的性能较差,惯性因子ω 应设置很大,从而加强了粒子的搜寻能力,更快更精确地向最优解(C,σ)靠近。为使这些粒子在进化前期较长时间内保持很强的大范围搜索能力以提高搜索效率,在进化中期有较小范围的精细搜索以提高搜索精度,后期又能快速收敛到全局最优位置。因此在Shi Y 提出的线性递减动态调整惯性因子的策略

的基础上进行改进,并引入正弦函数,非线性递减动态的调整惯性因子,从而可以很好地表示这些粒子的ω 大小变化。即:

综上所述,自适应调整第i 个粒子的惯性因子ωi的计算公式为

式中:k=1,2,…,A;ωi为第 i 个粒子的惯性因子。
1.4 粒子群优化支持向量机参数
采用MPSO 算法对SVM 中的参数C 和σ 进行优化,算法原理图如图1 所示。

图1 MPSO-SVM 算法流程图Fig.1 Flow chart of MPSO-SVM algorithm
MPSO-SVM 算法主要步骤为:
(1)将所有样本数据分为两部分,即训练数据和测试数据;
(2)初始化粒子群,主要包括PSO 的参数ω、c1、c2、A 和 n,设置适应度误差 e,并设置 SVM 分类器参数范围,即惩罚因子C 的范围[Cmin,Cmax]、核函数参数σ的范围[σmin,σmax]、初始化粒子的位置 xi0和速度 vi0以及每个粒子各自的最优位置pi和pg;
(3)计算出每个粒子的新的适应度值fi,根据式(8)选择合适的惯性因子,完成粒子位置和速度的更新;
(4)将粒子的适应度值 fi与 pi时的适应度值f(pi)进行比较,若fi>f(pi)或满足|fi- f(pi)|≤e 且C(xi)<C(pi),则更新pi,将粒子的适应度值与pg时的适应度值f(pg)进行对比,若fi>f(pg)或者满足|fi- f(pg)|≤e 且C(xi)<C(pg),则更新pg;
(5)判断进化次数a 是否小于或等于最大进化次数A,若小于或等于则返回到(3),否则结束进化过程;
(6)输出最优解(C,σ),并创建 SVM 分类器,进行模型训练和分类预测。
2 下肢多源信息采集系统
2.1 信息采集
本文选取6 位年龄均为22~26 岁健康的在校研究生作为受试者,所有受试者都不存在下肢运动损伤或其他影响下肢正常运动的疾病。在信息采集时,将表面肌电信号与髋关节角度、加速度的采集频率都设置为1 kHz,用以保证信息采集的同步性。同时,本实验利用高速相机记录下实验者实验过程,用于判断运动起止时刻,以及记录下髋关节运动角度,与BWT901CL型姿态角度传感器记录的角度进行对比,避免角度记录出现偏差。经试验测得髋关节活动范围[-65°~85°]。
2.1.1 肌电信号采集
图2 为测量肌肉和行走时的肌电信号图。

图2 肌电信号采集Fig.2 EMG signal acquisition
根据下肢肌肉肌电信号强弱和肌肉相似度大小的原则,选取股直肌、股内侧肌、半腱肌和腓肠肌等四块肌肉作为肌电信号采集对象,如图2(a)所示。使用非侵入式表面电极、NI9205 采集卡和四通采集电路组成的采集系统对表面肌电信号进行采集,采样频率为1 kHz,信号经滤波电路输出,如图2(b)所示。实验中,实验者在规定的时间内完成特定距离的平地自然行走,记录下行走时四块肌肉的肌电信息、髋关节角度和下肢加速度大小。
2.1.2 髋关节角度及加速度采集
本实验采用了BWT901CL 型姿态角度传感器,该传感器配合动态卡尔曼滤波算法,在动态环境下测量精度0.05°,可同时输出x 轴、y 轴和z 轴的加速度信息和髋关节角度。实验时,规定被测试对象在2.5 s 内,沿同一直线走过相同距离,采集的信息作为有效活动信息。
2.2 特征提取
2.2.1 下肢表面肌电信号特征提取
肌电信号、加速度特征值的提取是进行关节角度预测的基础,特征值选取是否合理直接影响预测结果。
目前,针对sEMG 信号的处理方法主要有时域分析和频域分析方法两个方面。本实验选择时域分析法中最能反映肌电信号特征的均方根值(root mean square,RMS)和积分肌电值(integral EMG)而后者又取决于肌肉负荷性因素和肌肉本身的生理、生化过程之间的内在联系[14]。因此,上述时域分析指标常被用于实时地、无损伤地反映肌肉活动状态,具有较好的时效性。
RMS 值和iEMG 值的计算公式分别为:

式中:xi为单通道 sEMG 信号序列,i=1,2,…,N;N 表示用来计算特征值的肌电信号序列长度,本文选择N=60 个样本点。
在对sEMG 信号进行特征值提取时,采用移动窗分割的方法,如图3 所示。

图3 肌电信号数据分割方式Fig.3 EMG signal data segmentation method
以股直肌为例,窗长度为L,每次平移a 个长度。为提高数据鲁棒性,保证满足a=L/2 条件,确保每次都有一半信号是叠加的。
2.2.2 下肢加速度特征提取
加速度传感器能够采集人身体三轴方向的加速度,根据人体运动时其三轴方向的加速度会发生变化,身体运动越剧烈,其合加速度越大。因此提出信号幅度域(SMA)表征单位时间内身体运动剧烈程度[15-16],其公式为:

式中:T 为移动窗时间宽度,本文选择T = 0.3 s,即60 个采样点与表面肌电信号特征值提取保持相同时间。加速度SMA 值与髋关节角度如图4 所示。

图4 加速度的SMA 值与髋关节角度值Fig.4 Acceleration SMA value and hip joint angle value
2.3 多源信息特征值融合
按上述方法进行特征提取,可得40×9 维特征矩阵,为将肌电特征值与加速度特征值进行更好融合,并降低特征矩阵维数,本文采用主成分分析算法进行特征值的融合。主成分分析(PCA)是一种数据压缩和特征提取的多元统计分析技术,旨在利用降维的思想,把多指标转化为少数几个综合指标[17-18]。从结果中提取前9 个主成分累积贡献率达到90%,可概括原始特征值,取前9 个主成分为筛选后的特征值,见表1。

表1 主成分的累积贡献率Tab.1 Accumulative cumulative contribution rate of principal component
3 关节角度预测结果及分析
本研究的目的是提出一种改进的MPSO 优化算法对SVM 算法进行优化,使用优化后的SVM 算法进行关节连续运动预测,通过对6 位为受试者的实验数据的采集,验证该算法的有效性,并将改进算法的预测结果与SVM 算法和BP 神经网络等算法的预测效果进行对比。为评估预测方法的准确性,本研究采用均方根误差(R)来评估关节角度预测值与关节角度测量值之间的相似程度。设θˆ为髋关节实际测量值θ 的预测值。均方根误差为:
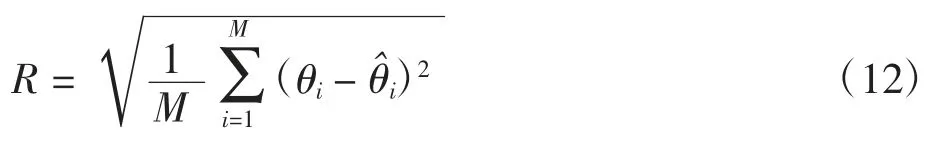
式中:M 为关节角度样本数;θˆi为第 i 个关节角度预测值;θi为其实际测量角度。
将2 000 个样本数据分成2 份:一份1 200 个作为模型训练数据;另一份800 个样本作为实际试验数据。经改进后的MPSO-SVM 算法可准确预测不同时刻人体正常行走时髋关节角度变化趋势,并精确地预测出该时刻的运动角度,如图5 所示。

图5 改进的MPSO-SVM 算法预测结果Fig.5 Prediction results of improved MPSO-SVM algorithm
为进一步验证该改进算法的优越性,本实验设置了与SVM 算法和BP 神经网络算法两个算法的对照试验。同等条件下,参数设置一致,并且模型训练样本和测试样本完全一样的情况下,使用SVM 算法和经典的BP 神经网络算法对髋关节角度进行预测,结果如图6 所示。

图6 预测结果对比Fig.6 Comparison of prediction results
本实验使用均方根误差R 来评估预测值与实际值的精确程度,如表2 所示。

表2 所有对比结果精确度统计Tab.2 Accuracy statistics for all comparison results
为更加全面衡量该算法效果,表2 中增加了对算法预测结果的最大绝对误差和平均误差的记录。由表2 可见,改进的MPSO-SVM 算法在800 个测试样本中最大绝对误差为7.72°,平均误差为1.40°,均方根误差2.67。由此可见,改进的MPSO-SVM 算法的预测效果和精确度远远优于SVM 算法和BP 神经网络算法的预测结果。
4 结 论
人体连续运动关节角度的预测对康复机器人的研究至关重要,如何提高人体连续运动关节角度精度是研究重点。得到主要结论如下:
(1)本文通过对6 名在校研究生进行数据采集实验,采集受试着在做适度行走时左腿股内侧肌、股直肌、半腱肌和腓肠肌等四块肌肉肌电信号,以及下肢加速度信号和髋关节角度信息。将所采集的原始信息进行预处理和特征提取。为提高原始信息的利用效率,以及降低特征矩阵维数,本实验利用主成分分析算法(PCA)将肌电信号的特征值和加速度特征值所组成的特征矩阵进行降维处理,利用降维后的特征向量进行髋关节角度预测。
(2)为解决下肢连续运动情况下关节角度预测精度低的问题。本文提出改进的MPSO-SVM 算法,通过引进正弦函数和指数函数,对PSO 算法的惯性因子ω进行优化,增强PSO 算法全局和局部寻优的协调能力,从而实现对SVM 算法的最佳优化效果。从预测结果分析,改进的MPSO-SVM 算法预测的均方根误差为2.67,远远小于SVM 算法的21.27 和BP 神经网络的 23.60;平均误差为 1.40°,小于 SVM 算法的 8.02°和BP 神经网络的13.59°;针对每一时刻预测效果而言,改进的MPSO-SVM 算法的最大绝对误差为7.72°,预测误差仅为髋关节角度范围的5.51%,更是优于SVM算法的41.7%和BP 神经网络的45.49%。
(3)改进的MPSO-SVM 算法可有效改善下肢连续运动情况下髋关节角度预测精度低的问题。但本实验仅对在校研究生进行实验,为进一步提高该算法的预测精度,还需更多实验进行验证。

