基于认知跟踪的集中式MIMO雷达功率分配算法

李正杰，谢军伟，张浩为

(空军工程大学防空反导学院，陕西 西安 710051)

0 引言

集中式多输入多输出(MIMO，Multiple Input Multiple Output)雷达作为一种新体制雷达，拥有比传统相控阵雷达更优越的分辨特性、更强的低截获能力和抗干扰能力等优点，得到了研究人员的广泛关注。通过在发射端同时发射多个正交信号，在接收端引入数字波束形成技术(Digital Beam Forming，DBF)，集中式MIMO雷达能够同时生成多个正交波束，可实现同时多波束，从而对多批目标进行定位跟踪[1]。

目标跟踪精度与雷达发射功率、有效带宽、目标RCS参数均有关系[2]。认知跟踪将各目标状态信息及时反馈给发射端，实现根据目标特性自适应地选择雷达发射信号参数配置，提高目标跟踪能力。在实际中，雷达发射功率受到载荷和能源的限制。如何合理分配有限的发射功率从而获得更好的目标跟踪性能，已经成为认知跟踪领域的热点问题。在实际运用中，雷达功率分配通常将发射总功率恒定作为约束条件，优化调整各波束发射功率，获得最佳目标跟踪精度[3]。功率分配算法的有效性很大程度上依赖于目标位置的估计精度[4]，因此运用恰当的性能界限评价运动目标的估计误差精度具有重要意义。理论上讲，克拉美罗下界(Cramer-Rao Lower Bound, CRLB)能为任何无偏估计量的最小方差提供一个下界；但CRLB不具有预测能力，不能适用于运动目标功率分配场景。文献[5]证明了后验CRLB(Posterior-CRLB，PCRLB)的预测能力，提出可将PCRLB应用于运动目标跟踪场景。文献[6—7]分别利用扩展卡尔曼滤波(Extended Kalman Filter，EKF)和精度更高的无迹卡尔曼滤波(Unscented Kalman Filter，UKF)，提出了跟踪单个运动目标的功率分配算法。利用PCRLB的可预测性及其与发射功率的关系，可将其作为代价函数构建功率优化模型。现有研究中，利用PCRLB构成代价函数可以分为两种：一是综合考虑各目标的PCRLB，对各目标跟踪精度之和进行优化；二是只考虑精度最差目标的PCRLB，仅对最差目标跟踪精度进行优化。关于功率优化模型求解问题，文献[8—9]将功率分配看作非凸优化问题，利用贪婪算法来寻求最优解。上述研究及算法存在以下缺陷：一是将功率分配看作非凸优化问题，导致运算量增大而且可能得不到最优解；二是采用的跟踪算法精度不够高，导致功率分配结果误差增大；三是现有研究大都直接运用两类代价函数中的一类，并未对两种函数的结果进行分析。对此，本文针对集中式MIMO雷达执行多目标跟踪任务时，现有功率分配算法计算量较大且准确性较差的问题，提出了基于认知跟踪的集中式MIMO雷达功率分配算法。

1 同时多波束机制下的跟踪模型

1.1 同时多波束工作机制

同时多波束工作机制是集中式MIMO雷达区别于传统相控阵雷达的重要工作方式，能够让雷达同时对多个目标进行跟踪，示意图如图1所示。该工作机制的数学描述如下：

假设x-y平面内，集中式MIMO雷达位于点(x0,y0)，同时发射多个正交信号对Q个运动目标进行跟踪，且各波束仅用于跟踪一个目标。在窄带条件下，k时刻雷达向第q个运动目标发射的信号为：

(1)

式(1)中，fc为载波频率，q=1,2,3,…,Q，Eq,k(t)为信号的复包络，Pq,k为发射功率，且满足：

(2)

信号的有效带宽和有效时宽分别表示为：

(3)

(4)

k时刻，接收机接收的目标q的回波信号为：

(5)

式(5)中，hq,k为目标的RCS；αq,k为衰减系数，与距离的四次方成反比，τq,k为信号的时延，fq,k为目标相对雷达的多普勒频率，nq,k(t)为零均值的高斯白噪声。

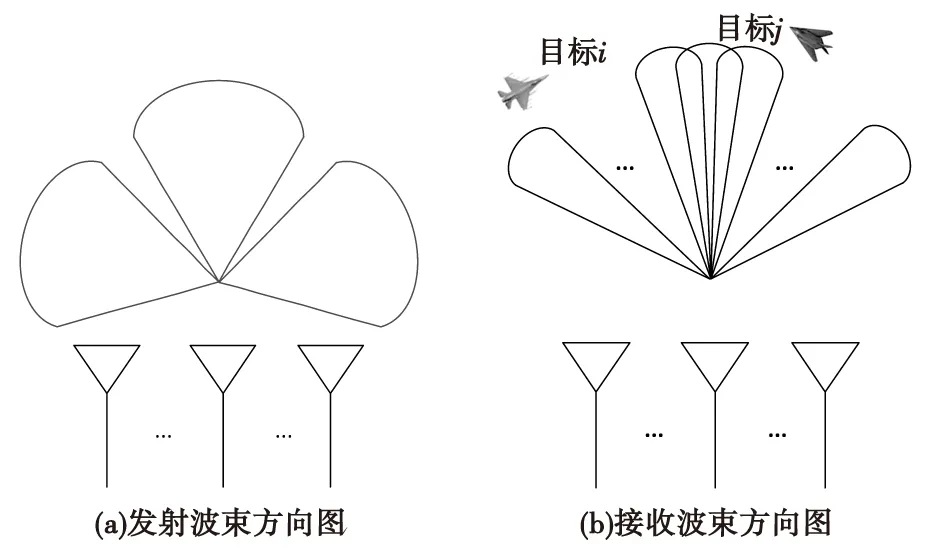
图1 同时多波束示意图Fig.1 Simultaneous multi-beam schematic diagram

1.2 运动模型

假设Q个运动目标彼此分离，且都在做匀加速运动，则第q个目标的运动方程可表示为：

(6)

(7)

(8)

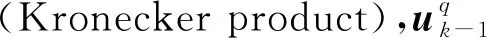
(9)

式(9)中，Ts表示采样间隔;sq表示过程噪声的强度。

1.3 观测模型

假设该集中式MIMO雷达能稳定接收各目标的回波信号，并能从回波信号中提取各目标相对雷达的径向距离、速度、方位角以及目标RCS等信息。k时刻，第q个目标的观测向量和目标状态向量的关系可表示为：

(10)

式(10)中，hq,k(·)表示k时刻目标q的观测方程：

hq,k(·)=[hRq,k(·),hfq,k(·),hθq,k(·)]T

(11)

因此观测向量的维数为nh=3，式(11)中的各项可表示为：

(12)

式(12)中，λ表示雷达的工作波长，rq,k，fq,k，θq,k分别代表k时刻目标q与雷达之间的径向距离、多普勒频率和方位角。

式(10)中的vq,k代表均值为零的高斯白噪声，方差为：

(13)

(14)

式(14)中，B为接收波束的宽度。

由式(14)可知：由于衰减系数αq,k与距离的四次方成反比，且与测量方差成反比，因此目标与雷达间径向距离越远，目标跟踪精度越差；目标RCS与测量方差成反比，因此目标RCS越小目标跟踪精度越差；发射功率Pq,k与测量方差成反比，跟踪第q个目标的波束功率越大，雷达测距、测速、测角精度越高。

至此，zq,k的概率分布可表示为：

(15)

依据贝叶斯定理：

(16)

结合式(6)和式(10)可迭代计算出，目标状态的后验概率密度函数(PDF，Probabilistic Density Function)，从而可以对目标状态进行估计。由于观测方程是非线性的，在估计目标状态时，往往得不到后验概率密度的精确解，需要通过非线性滤波算法进行近似求解。本文选用结构简单并且估计精度高的SRCKF算法对目标状态进行估计。

衡量非线性滤波问题的精度，可以通过求解均方误差下界实现。理论上讲，CRLB可以对任何无偏估计提供均方误差下界，但其本身不具备预测能力，因此不能对运动目标提供有效的下界。文献[10—11]在CRLB的基础上提出PCRLB，利用PCRLB的可预测能力对运动目标跟踪精度进行预测，从而可产生针对运动目标跟踪精度的有效下界。

2 基于认知跟踪的功率分配算法

2.1 PCRLB的递推式

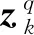
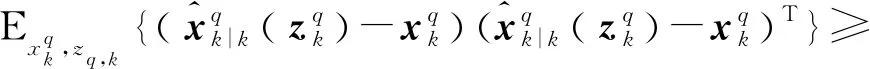
(17)

式(17)中，E(·)代表求数学期望，Jq-1(k)表示k时刻，第q个目标的PCRLB，即Fisher信息矩阵(FIM，Fisher Information Matrix)的逆。

(18)

(19)

PCRLB的递推式可表示为[12]：

(20)

(21)

(22)

(23)

(24)

由于状态方程为线性，而测量方程是非线性的。可将式(20)简化为：

(25)

(26)

(27)

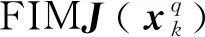
(28)

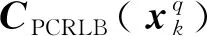
(29)

(30)

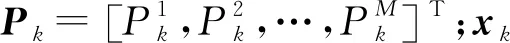
两种代价函数各有特点：式(29)更多地关注多目标整体的跟踪精度；式(30)更关注最差目标的跟踪精度。实际中应结合具体场景和任务要求来选择代价函数，但从广义上讲，无论选择何种代价函数，均能体现k时刻雷达的跟踪精度。

2.2 优化模型的建立及求解

由式(27)可知，目标跟踪精度受很多参数影响，如目标的RCS、信号带宽以及发射功率等。本节针对雷达发射功率分配问题进行研究，在雷达发射总功率Ptotal固定的情况下，对各跟踪波束的发射功率进行优化分配，从而提高目标跟踪精度。根据代价函数不同，建立Φ1、Φ2两种优化模型：

(31)

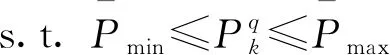
(32)

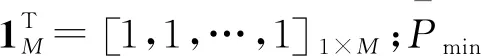
求解凸优化问题的传统方法有贪婪算法、内点法、梯度投影算法等。传统算法均需要进行多次迭代搜索，耗费时间较长。文献[15]提出利用SDP算法可以将凸优化问题转化为容易求解的SDP问题，从而实现快速实时求解。基于提高功率分配实时性需求，采取优化速率更快的SDP算法。现以F1模型为例，描述SDP算法流程。

将式(28)带入式(29)可得：

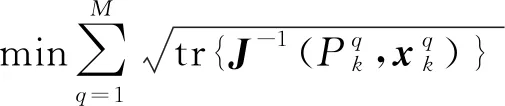
(33)

为求解式(33)，设置一个辅助矩阵Mq，将其代替代价函数，并且增加限制条件：

(34)

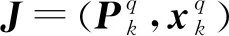
(35)

便可得到一个与式(33)等价的SDP问题：

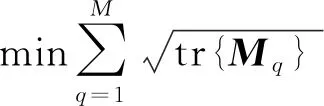
(36)

至此，F1模型的凸优化问题已转化为SDP问题，同理可将F2模型的凸优化问题也转化为SDP问题。转化完毕后，利用SeDuMi工具箱可分别对两个优化模型进行求解。

3 仿真实验及结果分析

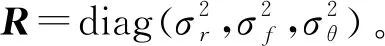
(37)

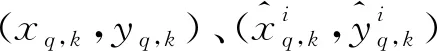
为进一步对比分析两种代价函数对分配结果和跟踪精度的影响，以及验证所提功率分配算法的有效性，设置三种模型进行仿真，记为(P1,P2,P3)。其中，P1表示以式(30)为代价函数构成的最差目标的PCRLB优化模型，P2表示以式(29)为代价函数构成的各目标总的PCRLB优化模型，P3为功率平均分配模型。在初始时刻，P1与P2模型均为平均分配。

为探究距离和目标RCS对功率分配结果的影响，设置两种RCS模型，记为(H1,H2)。其中，H1表示各目标RCS值恒为1；H2为各目标RCS各不相等，且出现起伏，具体数值见图3。

表1 初始时刻目标运动参数Tab.1 The parameters of targets motion at the initial time

表2 雷达与发射信号参数Tab.2 The parameters of radar and transmitting signal

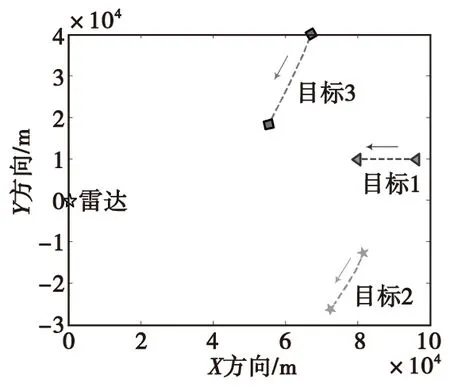
图2 雷达与目标的空间分布Fig.2 Spatial distribution of radar and targets

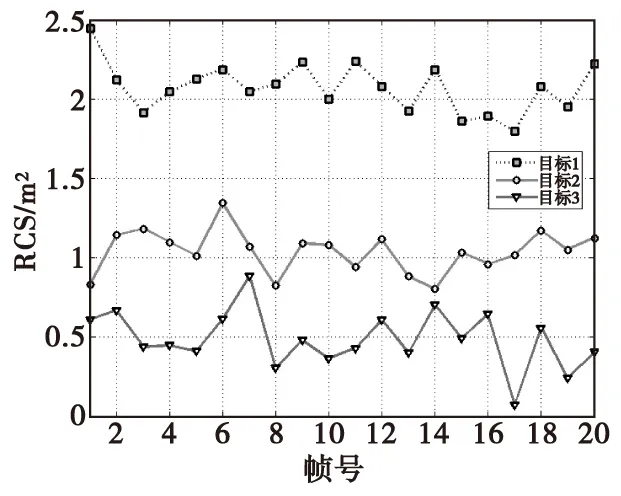
图3 第二种RCS模型H2Fig.3 The second RCS model of H2

场景1 距离影响

在此场景下，RCS模型为H1，即各目标RCS值均为1。因此，雷达功率分配仅与雷达到目标的径向距离及其相对位置关系有关。

图4(a)—图4(c)分别给出了不同功率分配模型下，各目标位置的PCRLB之间的关系。由图可知，P1模型各目标PCRLB值最接近，因此各目标跟踪精度相差最小；P2模型各目标PCRLB值较接近，各目标跟踪精度相差较小；P3模型各目标PCRLB值相差最大，各目标跟踪精度相差最大。

图4(d)和图4(e)中，不同颜色表示不同的发射功率比，定义为：

rq,k=Pq,k/Ptotal

(38)

由于目标1距雷达最远，在P1和P2两种优化模型下，目标1均获得最多的发射功率。

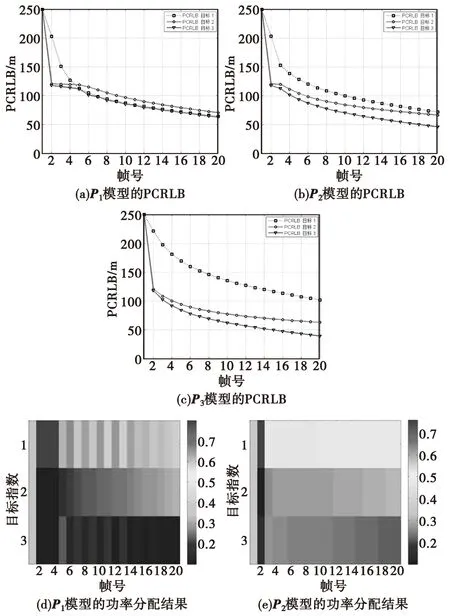
图4 场景1中不同功率分配模型下各目标PCRLB及功率分配结果Fig.4 The PCRLB and power distribution results of each target under different power distribution models in Scenario 1

图5给出了三种分配模型下，各目标总的PCRLB与RMSE、最差目标的PCRLB与RMSE之间的关系。结果表明：P2模型下各目标PCRLB之和最小，并且总的RMSE最小，因此总的跟踪精度最高；P1模型下最差目标PCRLB最小，随着时间推移，P1模型的RMSE也逐渐小于P2模型；在H1模型下，无论是经P1还是P2优化模型处理过后，总的跟踪精度和最差目标的跟踪精度都比P3模型高。

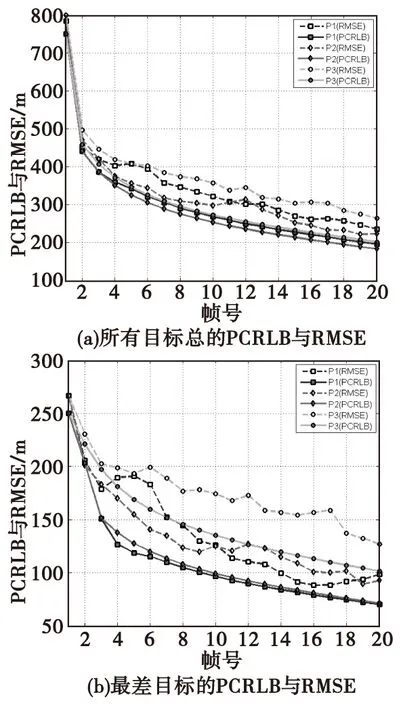
图5 场景1中不同功率分配模型下跟踪性能对比Fig.5 The comparison of tracking performance under different power distribution models in Scenario 1

场景2 目标RCS影响

在本场景中，RCS模型为H2，即各目标RCS值均不相等且发生起伏变化。因此，影响雷达功率分配的因素除雷达与目标的径向距离及相对位置关系外，还有各目标的RCS值。

图6(a)—图6(c)给出了RCS起伏模型下，经不同分配模型处理后各目标的PCRLB。结果显示：P3模型下，由于目标3的RCS最小，目标3的跟踪精度最差；P1模型能够有效提升最差目标的跟踪精度，并且使各目标的跟踪精度很接近；P2模型能够在一定程度上减小最差目标的跟踪精度，使各目标的跟踪精度较为接近。

图6(d)—图6(e)给出了P1与P2模型的功率分配结果。相较场景1，场景2中虽然目标3距离雷达最近，但RCS最小，最终使得目标3成为精度最差的目标，因此绝大部分功率分配给了目标3。

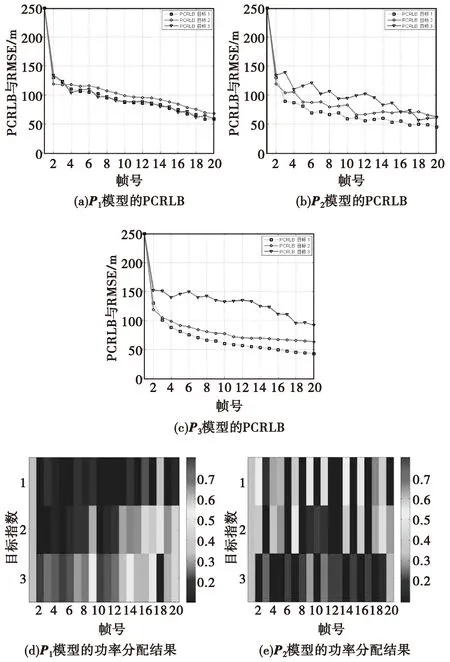
图6 场景2中不同功率分配模型下各目标PCRLB及功率分配结果Fig.6 The PCRLB and power distribution results of each target under different power distribution models in Scenario 2

图7(a)给出了H2模型下，经各优化模型处理后各目标PCRLB之和以及RMSE之和的关系。结果表明：当RCS出现起伏时，P2模型下所有目标总的PCRLB值以及总的RMSE仍然最小，因此总的目标跟踪精度仍然最高；在P1和P3模型下，总的目标跟踪精度相差不大。

图7(b)给出了H2模型下，经各优化模型处理后最差目标PCRLB之和以及RMSE之和的关系。结果表明：当RCS出现起伏时，在P1和P2模型下最差目标的PCRLB相差不大，但是P1模型下最差目标的PCRLB更加平滑，最差目标的RMSE起伏更小；P1和P2模型下的最差目标精度均高于P3模型。

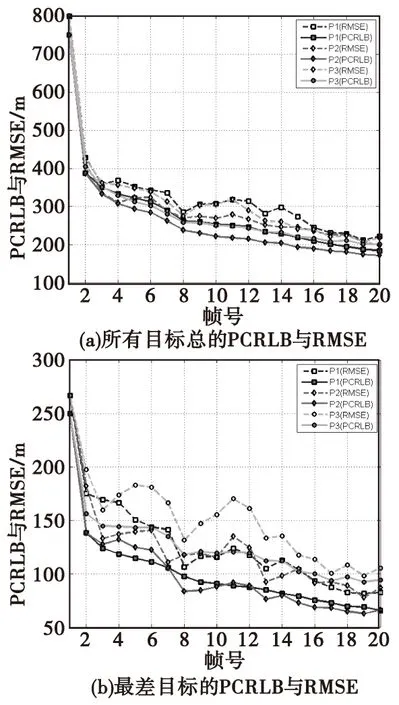
图7 场景2中不同功率分配模型下跟踪性能对比Fig.7 The comparison of tracking performance under different power distribution models in Scenario 2

4 结论

本文提出了基于认知跟踪的集中式MIMO雷达功率分配算法。该算法首先推导了运动目标位置误差的PCRLB，而后对PCRLB进行预测并将其作为代价函数，从而将功率分配问题转化为凸优化问题。最后运用SDP算法将凸优化问题转化为SDP问题并求解。为探究总目标跟踪精度和最差目标跟踪精度两类代价函数以及目标RCS值对功率分配结果的影响，设置了对照仿真实验。

实验结果表明：1)在功率优化分配模型中，距离雷达较远、RCS较小的目标通常分配较大的发射功率；2)当目标RCS起伏时，目标跟踪精度也会随之出现起伏；3)相较于功率平均分配，本文提出的总目标跟踪精度优化模型能明显提高各目标总的跟踪精度，最差目标跟踪精度优化模型能明显提高最差目标的跟踪精度；4)总目标跟踪精度和最差目标跟踪精度两种优化模型各有优势：前者能使总的目标跟踪精度达到最小，有时也可使最差目标跟踪精度达到最小，后者能使最差目标跟踪精度起伏幅度明显小于前者，并且能够使各目标跟踪精度更为接近。