EBSN中基于用户特征的社交事件规划与饥饿问题处理

张翰林，丁琳琳，王俊陆，宋宝燕

(辽宁大学 信息学院，沈阳 110036)

1 引 言

近年来，基于社交事件的社交网络(Event based Social Networks)作为一种提供在线社交事件信息的社交网站，越来越受到人们的青睐，如Meetup(1)http：//www.meetup.com、Plancast(2)http：//www.plancast.com等.在EBSN中如何根据用户对事件的感兴趣程度，为用户制定一组科学合理的社交事件集，是当前的研究热点[1-3].目前很多算法的规划通常从用户与事件两个方面考虑，从用户角度考虑，每个用户对每个事件有一个兴趣值，每个用户的总体旅行预算[2]或用户的空闲时间；从事件角度考虑，社交事件集中事件间的关系[3]，用户参与事件的时空冲突[2，4,5]，事件的发生时间段与资源约束[3].算法的评判标准大多集中在计算“总效应值”[2，4，5]上，即将所有用户的所有规划集中事件的兴趣值相加，该值越大，则表明规划算法的表现越好.若从用户角度考虑，利用贪心策略进行规划，则多数算法没有考虑用户本身的特征，没有对用户排序，导致规划结果不够优化；若从事件角度考虑，当事件容量不够时，有些用户始终无法获得事件，导致用户对社交网站的满意度下降.

针对上述问题，本文提出一种基于用户特征的社交事件规划与饥饿问题处理方法.主要贡献：1)提出一种离线的基于用户特征的社交事件规划算法，结合贪心思想，优化了用户的处理顺序，较传统贪婪规划算法提高了总效用值；2)提出一种解决用户饥饿问题的规划算法，解决全局社交事件规划算法出现的饥饿问题，提高了用户满意度；3)在Meetup合成数据集上的实验表明，本文所提基于用户特征的规划算法在性能和总效用值表现较好，救济算法能够有效消除饥饿用户.

2 相关工作

目前事件规划算法主要从单一用户角度进行规划、用户组角度进行规划及对每一个用户推荐一组满足约束的事件集三个方向进行研究.

A.MÜNGEN等人[6]基于用户参与事件的历史与用户感兴趣的领域给用户推荐社交事件；H.YIN等人[7]通过分析用户间的社交关系推荐给好友最相似的事件；高泽锋等人[8]提出一种结合LDA主题模型的推荐算法，结合时间函数和行为权重进行事件推荐；以上研究工作对单一用户进行社交网络事件的推荐，假定用户彼此之间没有联系，忽略了用户间的紧密交互性，且单一事件推荐无法满足当前社交网站大量事件的现状.

Z.WANG等人[9]提出一种基于内容感知的组成员社交影响推荐模型，按照社交影响给组成员推荐社交事件；S.PURUSHOTHAM等人[10]提出一种基于协作过滤的贝叶斯模型，捕获用户组中用户的信息，用于个性化的组事件推荐；Y.JHAMB等人[11]从用户和事件的角度考虑，通过Logistic与Proitsigmoid函数建立个性偏好的概率模型，但实际偏好很难通过单一模型进行估计.

Y.CHENG等人[4]综合考虑事件容量与用户能参与事件的个数，利用贪婪算法的思想，对事件集与用户集进行全局社交事件规划；J.SHE等人[2]提出考虑发生时空冲突时，用户与事件如何分配使得全局效用值最大的算法，但当事件容量不够时，无法获得事件的用户满意度会下降；J.SHE等人[5]进一步提出了根据新事件或用户的属性调整全局社交事件规划的算法.K.LI等人[12]提出了SEO问题，考虑了用户个人与用户间对事件的亲密度；B.NIKOS等人[3]提出了SES问题，考虑了用户间的社交关系和事件的影响力，B.NIKOS等人[13]在SES问题的基础上进一步提出了识别和分配适当的时隙，从而使参加活动的人数最大化；成雨蓉等人[14]提出了一种从用户与事件两个角度考虑的偏好稳态规划，提出了阻塞对的概念，但以上工作中若出现一些兴趣值较小的用户时，不优化用户的处理顺序将会出现兴趣值较高的用户由于事件满容量而无法参与她最感兴趣的事件的情况，导致规划结果的不合理.

3 基于用户特征的社交事件规划处理方法

USEPT问题是NP难问题[1]，离线的社交事件规划已知用户与事件的相关属性，已知用户对事件的兴趣值，对用户进行社交事件规划，无论从事件角度，或从用户角度考虑，规划的目标是使总效用值最大化，因此，本文提出基于用户特征的社交事件规划方法，优化用户处理顺序，实现离线社交事件规划.

3.1 问题描述

定义1.(用户和事件)社交网络中的事件集E={ei|i∈[0,|E|]}，其中i是事件的无序序号，|E|表示事件的总数量.社交网络中的用户集U={uk|k∈[1,|U|]}，其中k，表示用户的无序报名顺序序号，|U|表示用户的总数量.

设现有5个已报名加入参与事件的用户u1～u5，有6个事件等待分配给这些用户e1～e6，即规划5个用户如何合理地参与这6个事件的问题.假设每个用户对每个事件有一个兴趣值，即每个事件存在一个最感兴趣的用户，每个用户同样如此，用户和事件的位置如图1所示.

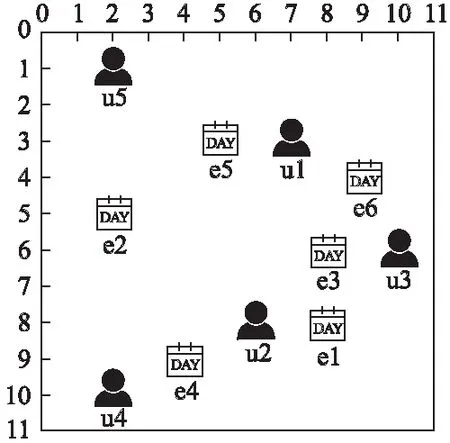
图1 用户与事件的位置关系Fig.1 Location between users and events

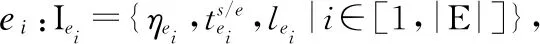
表1 用户事件对表
Table 1 User-event pair

SU=3u1(0-171)u2(1-50)u3(2-50)u4(2-34)u5(1-10)事件发生时间e1(2)0.70.60.70.90.52-3e2(3)0.40.60.80.90.16-7e3(6)0.20.60.80.30.19-12e4(1)0.90.20.70.20.15-6e5(2)0.20.70.80.30.115-19e6(3)0.70.30.30.70.113-14

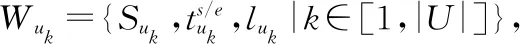
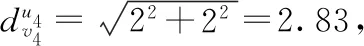
定义2.(用户平均移动速度与转场花费)每个uk有各自平均移动速度Suk，计算两相邻事件的转场时间花费，此值可根据历史统计值或数据挖掘得到，转场花费用公式(1)计算.

(1)

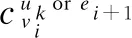
定义3.(位置)所有用户和事件均有一个经纬度信息lei=(xei，yei)/luk(xuk，yuk)，用于表示其实际地理信息，在计算距离时求欧氏距离，如公式(2)所示，即：

(2)

式中xuk、yuk分别表示用户uk的经纬度，xei、yei分别表示事件ei的经纬度，u↔e表示从用户uk的初始位置移动到某事件ei，e↔e表示用户从一个事件的位置到另一个事件的位置.

(3)

例，在传统贪婪算法规划中，当设置所有用户平均速度S=3时，事件e1最感兴趣的用户为u4，但u4空闲时间不满足，再找到u1，我们将事件e1加入u1的规划中，同时继续找u2、u5、u2满足约束，将e1加入u2安排中，再寻找e2适合的用户，u4符合约束，将e2加入u4中，继续找u2、u3，将e2加入他们的规划中，此时e2容量已满，因此我们寻找e3适合的用户，u3从e2出发到e3不满足时间约束，u2、u4同样不满足，u5空闲时间不满足，继续找u1满足约束，将e3加入u1安排，以此类推，得到全局规划：Pu2={e1，e2，e5}，Pu1={e1，e3，e4，e6}，Pu3={e2，e6}，Pu4={e2，e6}，Pu5={e6}，这样全局事件规划的兴趣总值(效用总值)为7.7.

定义5.(全局规划)一个合理可行的事件规划集中，单个用户的空闲时间真包含所有事件集的发生时间段，事件集中事件间的发生时间段没有交集，且满足转场时间花费，表示为：PU={Puk|uk∈U，k=1，2，…，|U|}.

3.2 基于用户特征的Skyline贪婪方法

每个用户对每个社交事件都有一个兴趣值，该值决定了社交事件分配的顺序，目前多数贪婪社交事件规划算法忽略了用户的处理顺序[2]，而提取用户特征可以将一些具有明显特征的用户区分开来，通过对这些特征进行排名，可以保证有最小的饥饿用户的同时，保证最大的总效用值.

对全体用户空闲时间内能参与的事件的个数进行从小到大的排序，并对用户空闲时间长短进行从短到长的排序，这样得到两个排序，按照公式(4)进行综合.其中Hvar是方差排名，IR是评价值排名.

AV=(Hvar+IR)/2

(4)

(5)

其中，ρei∈[0，1]是根据历年事件影响力的统计进行评估.将事件的持续时间作为分母，对于持续时间较长的事件，降低它们每次加入用户全局事件规划的可能性.

对全体用户空闲时间内参与事件的兴趣值求取方差，从小到大进行排序，并将评价值R求和进行由大到小的排序，得到两个排序，按照公式(6)进行综合，其中Hcount(e)是某用户空闲时间内参与事件个数的排名，Iidle是某用户空闲时间的长短排名.

AT=(Hcount(e)+Iidle)/2

(6)

参与事件个数越少，空闲时间越短，表明该用户更需要优先安排，可以减少饥饿用户；用户的空闲时间内能参与的每个事件的评价值的方差越大说明该用户的评价值相差越大，优先安排这类用户可以提高这类用户的满意度；兴趣值总和越大说明该用户爱好越广泛，优先安排这类用户可以使总效用值越大.

借鉴Skyline查询[16]多目标优化的特点，针对多目标即用户特征排序进行优化，通过对用户特征排序的同时，尽可能接近全局最优的结果，提出基于用户特征的贪婪规划算法(RGreedySkyline).算法流程如下：

Step 1.通过AV、AT这2个排名的组合，构成Skyline的查询二元组.迭代运行Skyline，为更准确的确定各个支配点的先后顺序，每次运行Skyline后求取各支配点与原点构成的面积由小到大排序，直至遍历所有点，得到最终的用户处理顺序，再利用贪婪思想对用户进行社交事件规划.

Step 2.引用先前工作[1]中RGPV算法的思想，先对用户大于平均值的事件进行规划，然后再规划小于用户平均值的事件.

3.3 算法与复杂度分析

基于3.2节提出方法的逻辑，给出伪代码实现及算法复杂度分析.算法伪代码如算法1所示.

算法1. RGREEDYSKYLINE

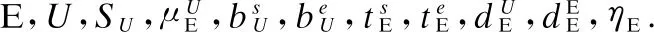
输出:A feasible global planPU.

1.cUE←dUE/SU,cEE←dEE/SU2.RUV←InitializeeveryRukeiby(5)3.PU←∅,q←aquerystoresallusers4.InitializeothervariablesinAlgorithm1,tmp,series,Hvar,Iμ,AV,Iidle,AT5.Tuplesofusers(AV,AT)6.While(qisnotnull)do7.tmp←BNL(tuplesofusersinq)8.Removetmp'susersfromq9.10.Sorttmpaccordingtotheareasurroundedbytheorigin(0,0)increasinglyseries←series∪tmp11.CallRGPVAlgorithmin[1]12.OutputPU;

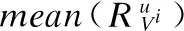
4 兴趣值不敏感的用户饥饿问题处理方法

规划算法中，可能由于一些兴趣值较高(敏感度较高)的用户占用了某个热门事件的名额，导致其他只能在空闲时间内参与该热门事件的不敏感的用户没有事件可参与的情况.为此，本文提出救济算法以解决该问题.

4.1 用户兴趣值敏感度

由于一些用户的兴趣值敏感度较高，抢占了过多事件资源，导致另一些兴趣值不敏感的用户始终无法拥有资源的现象称为饥饿，如在十一黄金周期间，某段时间内景点门票售罄，空闲时间只在该段时间内的游客都无法进入，此时这些游客均变成饥饿用户，若事先将空闲时间内可以参加其他事件的用户手中的票，匀给这些没有票的游客，则不仅用户的满意度上升，且总效用值下降不明显.在本文约束条件下，当某事件容量小于用户总数量时，可能发生饥饿.由于社交事件规划算法均是离线的，若某事件容量不足，在某些情况下产生饥饿用户几乎是必然的.

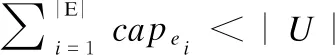
假设用户的空闲时间段相同，都包含全部事件集E，此时，按照贪婪算法的思想，从第一个用户开始进行全局社交事件规划，必定有用户无法参与事件，且经过救济算法后，每个用户均只参加了一个事件，但还是存在饥饿用户，所以推论1成立.同理，当某事件容量小于用户总数量时，总效用值不一定下降.

推论2.救济算法执行后，总效用值不一定减小，即：

或:

例如，文献[1]中的三个全局社交网络事件规划算法中，算法RDP得到的安排结果总效用值最大，但RGS算法中用户的排名与事件集的大小有关，若事件集过大，用户排名无法做到完全最优，所以，可能出现有些对某事件兴趣值较大的用户，未安排事件，导致饥饿的现象发生，因此总效用值不一定减小，推论2成立.

4.2 饥饿用户救济方法

针对上述问题，本文提出救济算法(RescueHunger)判断全局规划结果集中是否存在饥饿用户，调整全局规划事件集尽最大可能减少饥饿用户的数量，同时保证总效用值下降最小.

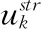
4.3 算法与复杂度分析

基于4.2节提出方法的逻辑，给出伪代码实现及算法复杂度分析.救济算法伪代码见算法2.

算法 2. RESCUEHUNGER

输出:A new feasible planPU.

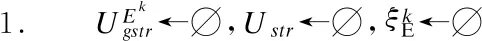
2.FindUstrin|U|orReturnPU

3.If|Ustr|=0ReturnPU

4.ForeachukinUstrdo

7.Foreachujin Ugdo

15.OutputPU

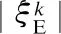
5 实验及分析

实验在通过与Meetup真实数据集进行合成的数据集上进行，对比算法为RDP算法和RG算法，并加入文献[1]中的预处理算法Pre，实验环境为Windows7操作系统，CPU为Intel 8核e3-1230 v5、3.4GHz、内存为8GB.

5.1 实验数据集与参量

真实数据集的分布情况如表2所示.原始数据包括：用户与事件的位置信息、事件的发生时间段；合成的数据段包括：

表2 数据集信息及影响因素表
Table 2 Data set information and effect factors in experiments

影响因素AlaskaLosAngeles事件平均容量实验变量设置|E|7031522851.0510,0.5k,1k|U|5600780050.7210,0.5k,1k

用户对事件的兴趣值(通过用户喜好标签与事件属性标签匹配个数、用户的空闲时间段、用户的平均移动速度、事件的最大容纳用户的数量(事件容量).其中，后三项是随机生成的.实验的主要评价标准为总效用分数(总效用值)大小与饥饿用户数量的变化，次要评价标准为运行时间.

实验参量设置如表2所示，分别改变事件数量、用户集数量，同时为线性实验，将每个事件的影响力设置为1，并将每个用户设置为相同的平均移动速度.

同时，检测了两个事件集的冲突率，如图2所示.

图2 数据集中事件的冲突率图Fig.2 Conflict ratio of event set in two data sets

从图2中可以看出，数据集的事件冲突率在事件数量增大时，没有较大的突变，维持在0.65-0.70之间，对于实验结果影响较低.

5.2 社交事件规划算法的评估

图3表示改变事件数量情况下RGS算法的性能.

从图3(a)和图3(b)可以看出，用户数量增大时，三个算法运行时间均增大.从图3(c)和图3(d)可以看出，用户数量增大时总效用值增大明显，由于事件容量较大，因此不会出现用户无事件可参加的情况.

图4为改变用户数量情况下RGS算法的性能.

如图4(a)和图4(b)所示，事件数量增大时，三个算法运行时间均增大.观察图4(c)和图4(d)可以看出，当事件数量达到2k时，在用户数量为200时，三种算法的效用总值下降明显，这是由于在增大的事件集中，用户更感兴趣的事件持续时间较长，占用了其他短时间事件的时间，每个用户参与事件的数量下降，所以效用总值下降.当用户数量增大时，弥补了事件无法充分安排的不足，当|U|=500时，效用总值不下降.

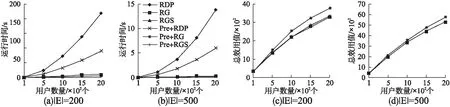
图3 改变用户数量评估RGS算法Fig.3 Change the number of users to evaluate the RGS algorithm

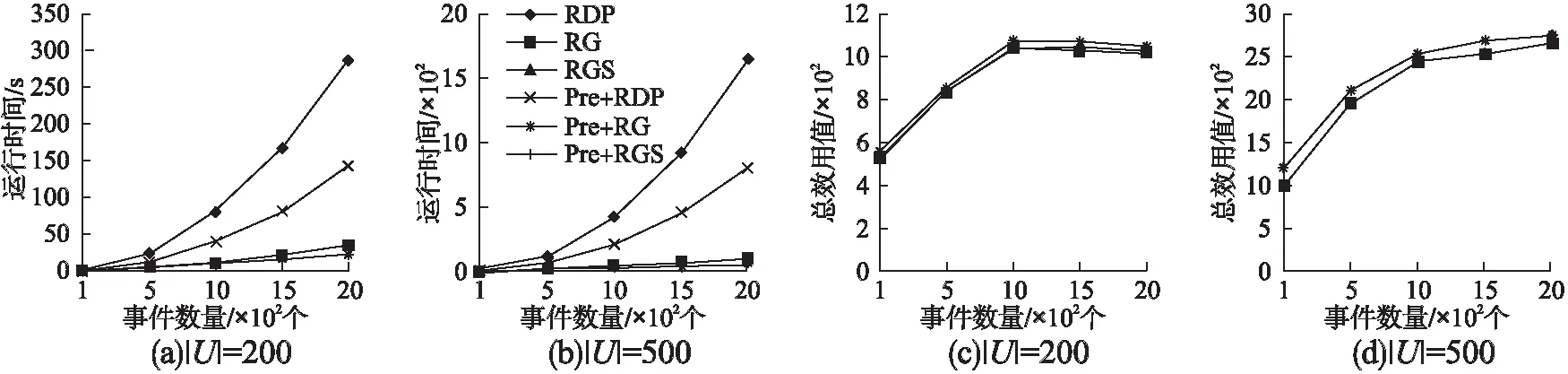
图4 改变事件数量评估RGS算法Fig.4 Change the number of events to evaluate the RGS algorithm

结论：尽管RGS算法的总效用值不如动态规划算法，但RGS算法的运行时间较RDP算法具有明显的优势，而RG算法的总效用值较RGS小，因此RGS算法的性能更优.

5.3 救济算法的评估

图5表示真实数据评估救济算法的总效用.

从图5(a)-图5(c)和图5(d)-图5(f)可以看出，随着用户数量的增长，在|E|=10时效用总值增长不明显，但|E|=100和|E|=1000时，总效用值增长较快，由于事件的总容量固定，虽然有更高兴趣值的用户加入，但总效用值仍受参与用户数量的限制，没有明显增长；当事件数量增大时，容纳用户数量显著增大，因此随着用户数量的增大，总效用值也随之显著增长；执行救济算法后，算法的总效用值在用户数量增大时下降，而RGS算法的总效应值却上升了，见推论2.

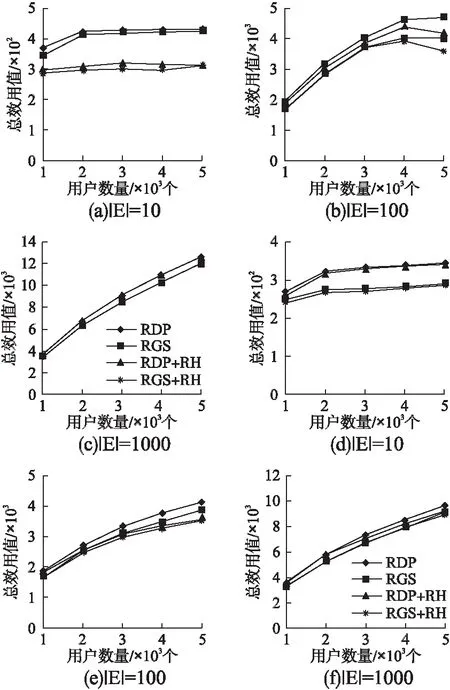
图5 真实数据评估救济算法的总效用分数图Fig.5 Real data to evaluate the total utility scores of the relief algorithm

图6为评估救济算法的运行时间.

对RDP、RGS两个算法的规划结果运行救济算法，从图6中可以看出，当饥饿用户较多且事件数量较少时，算法运行时间较少，同样当饥饿用户较多且事件数量较多时，算法运行时间也较少，但当饥饿用户与事件数量适中时，由于救济的用户数量上升，因此运行时间明显增大.

图7为评估救济算法执行后的救济效果.

从图7(a)-图7(c)可以看出，当|E|=10时，饥饿用户随着用户数量的增长明显增大，由于事件容量一定，因此用户数量显著增大时，饥饿数量明显上升，但由于候选救济用户几乎不存在，所以救济算法效果不明显.随着事件容量的上升(|E|=100、|E|=1000)，能容纳用户的数量上升，因此救济算法效果明显.

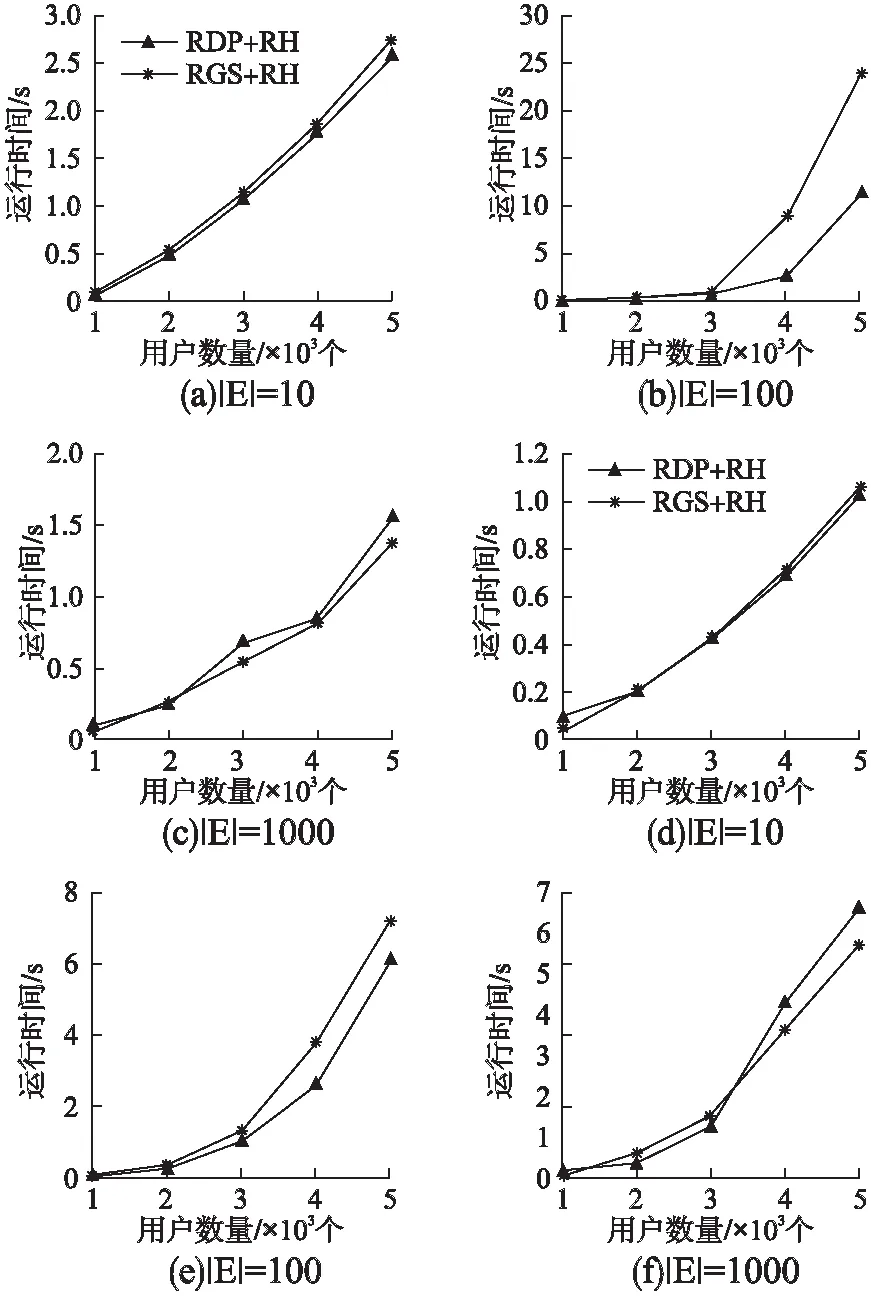
图6 真实数据评估救济算法的运行时间图Fig.6 Real data to evaluate the running time of the relief algorithm

从图7(d)-图7(f)可以看出，当|E|=100和|E|=1000时，执行救济算法后，饥饿用户数量显著下降，救济算法效果明显.

结论：通过三组评价指标，可以看出虽然RDP的规划结果总效用值较大，但执行救济算法后RGS的总效用值上升了；救济前，RDP的饥饿用户的数量较少，救济后，两个算法饥饿用户数量持平；因此RGS算法与救济算法结合表现更好.

6 结束语

本文通过提出一种与Skyline查询结合的社交事件规划算法RGS优化了贪婪算法中用户的处理顺序，合理地对具有不同特征的用户进行社交事件规划，较传统贪婪算法提高了总效用值；救济算法RH解决在特定约束下的全局事件规划中可能出现的饥饿现象，同样此思想可以应用到具有其他约束的规划算法中，通过救济算法对规划结果进行处理有效减少了全局规划中饥饿用户的数量，最大程度解决了由于其他爱好广泛的高兴趣值用户抢占事件资源的情况，最后通过在与Meetup真实数据集合成的合成数据集上的实验结果表明，本文提出的RGS算法能够有效的进行社交事件规划，RH算法能够有效解决全局规划算法中存在的用户饥饿问题.