一种单幅图像及其辅助曲线的三维建模方法

张 利，张 昊

(浙江工业大学 特种装备制造与先进加工技术教育部/浙江省重点实验室,杭州 310023)

1 引 言

三维建模在计算机图形学领域中具有极为重要的价值，到目前为止，三维建模软件性能已经十分强大.然而大多数三维建模软件专业性强，操作复杂，对没有专业知识的用户来说并不友好.而绘制图像要容易得多，大多用户都能通过图像来表达想法.

当前已存在许多基于图像的三维建模系统和方法.最典型和经典的是Igarashi等提出的Teddy[1]方法，根据图形骨架到边缘的距离计算三维空间点，由于此方法采用的是圆形的膨胀曲线，得到的三维模型横截面只能是圆形；此外，还有Zeleznik等提出的SKETCH[2]、Levi等提出的ArtiSketch[3]等三维建模系统和方法.这些建模方法往往在三维空间中完成，创建一个粗糙的三维模型，通过剪切、合并等操作为模型添加细节.然而，要从单幅图像中创建三维模型限制了这些操作.通过单幅图像创建三维模型主要问题在于如何解释图像、推断隐藏部分以及模型深度信息计算.Cordier[4]等提出了一种通过三维模型在二维平面上的投影来计算空间中的点位置的方法；此外，他们还提出了一种从存在模糊性的草图中重建三维模型的算法[5]，这些建模方法得到的三维模型横截面都是固定的形状，不利于体现用户建模的个性；Even E[6]等提出了一种从侧视草图中构建三维模型的算法，通过将手绘草图离散成各个循环的方式来构建三维模型和确定各部分深度信息；Saulo Ramos[7]等改进了Even E[6]的方法，将草图附近3D Hermitian数据的生成与识别和完成草图曲线的方法相结合，然后使用Hermitian径向基函数隐式曲面生成恰当的三维模型，达到捕获草图上更多细节的作用.缪永伟[8]等提出了一种基于图像对称性的花朵模型重建方法，并用圆锥拟合的方法改进该方法[9]；他们还提出了一种由二维线画图生成三维复杂零部件的三维建模方法[10].此外，Lee[11]等提出了利用二维线画图有效生成三维复杂多面体物体的方法，张淑军[12]等提出一种“二维草图自动生长技术”的建模方法，R.Suzuki[13]等提出了一种多人协作完成三维建模的方法.上述生成三维模型的方法以旋转[4,5]或膨胀[6,7]算法居多，用户无法随意设计三维模型横截面形状，导致实际建立的模型与用户的设计有一定的差距.本文通过辅助曲线获取模型深度信息，进而生成三维模型，用户不会受到横截面形状的约束，从而能生成的三维模型.

本文的主要贡献是提出一种通过寻找图形对称关系的基础上添加辅助曲线的图像三维建模的方法，生成的模型真实度和自由度有较大的提高.与以往沿着二维骨架对构造曲线进行广义旋转或膨胀得到模型表面不同，本方法以辅助曲线旋转、移动为基础得到模型表面.用户在绘制平面(z=0)绘制或导入图形，该图形是三维模型在绘制平面上的投影，这意

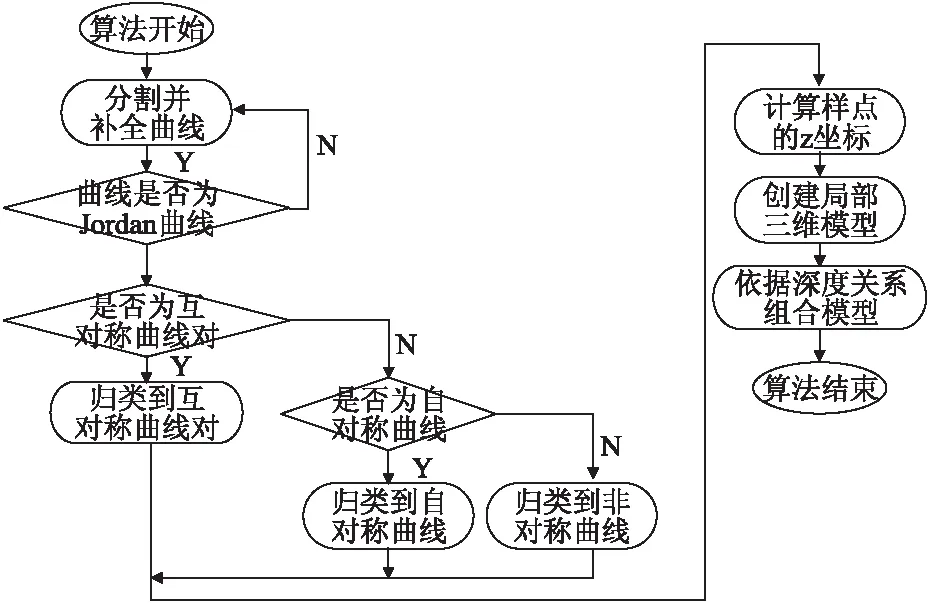
图1 算法流程Fig.1 Algorithm flow

味着三维模型上点的x和y坐标已知，只需计算点的z坐标.离散、补全曲线，得到的特殊点和图形中的转折点为特征点，计算曲线的对称关系，这将在第2、3节中介绍；通过添加对称面的方式来计算各特征点的三维坐标，这将在第4节中解释；得到特征点的三维坐标之后，根据辅助曲线来创建模型，这将在第5节中解释.算法流程如图1所示.

2 图像预处理

用户绘制或导入的矢量化之后的构造曲线[14](若存在相对于绘制平面对称部分，只需标记)即三维模型在绘制平面上的投影.直接使用二维图像进行三维建模存在一定难度，因此首先离散、补全二值化后的图像，之后绘制离散后各部分图像的辅助曲线.输入的图形由构造曲线Γ1和辅助曲线Γ2组成.

绘制完成后，我们还需要给定一个三维模型的对称平面，该平面与绘制平面不平行.

2.1 图像离散

曲线离散的依据是三种类型的特殊点[4,5]：T形结点、十字交点和尖点.T形结点是两条曲线交点的一种，定义为一条构造曲线与另一条构造曲线交叉时，一条构造曲线突然被截断而得到的交点，通常成对出现；十字交点定义为两曲线交错得到的交点，是两条曲线交点中最常见的一种；尖点是两个曲面相切所产生的切点，通常也成对出现.

2.2 补全曲线

本算法在构建模型时，各构造曲线需要封闭，因此需要将离散之后的构造曲线补全.构造曲线的集合为{Γ1,1,Γ1,2,…,Γ1,n}.检查各构造曲线是否闭合，将未闭合的曲线补全成闭合曲线，补充曲线的集合设为{Γ1,1′,Γ1,2′,…,Γ1,n′} .每一构造曲线都有对应的辅助曲线.若该构造曲线已闭合，则补充曲线长度为0.参考Karpenko和Hughes[2]的算法，完成隐藏轮廓的补全，即将输入曲线的端点互相连接成闭合曲线，补充曲线为二次Bezier曲线，该算法旨在通过找到其遮挡部分来重建完整的轮廓.重建得到的构造曲线Γ1,i与补充曲线Γ1,i′仍在同一水平面上.对各种特殊点之间的补充曲线进行说明：

1)对于两个T形结点之间：计算两个T形结点处的法向量，根据两个T形结点和法向量方向得到一个交点K，以上三点将作为控制点，绘制二次Bezier曲线Si.

2)对于两个尖点之间：计算两个尖点的切线向量的方向，并将两切线向量以两切点连线为对称轴进行对称，以对称后两切线向量的交点K和两个尖点作为控制点，绘制二次Bezier曲线.

3)对于一个T形结点和一个尖点之间，类似于文献[4]在本文中我们不考虑T形结点和尖点之间隐藏轮廓的重建.

4)对于两个十字交点之间：无需进行补充曲线，因为此时两条构造曲线是完整的.

构造曲线Γ1,i和补充曲线Γ1,i′一一对应，得到封闭的构造曲线.另外，补充完之后的构造曲线都是Jordan曲线，不存在自相交的情况，防止对建模产生影响.

3 寻找对称

寻找构造曲线的对称关系，本质上是寻找构造曲线的对称点，这是本方法中的一个难点.特征点由构造曲线上的特殊点和图形转折点组成.将补充完的构造曲线Γ1分成互对称曲线对集合Γ1,a、自对称曲线集合Γ1,b和一般曲线集合Γ1,c.在寻找对称关系之前，我们需要找到曲线上的转折点.

3.1 寻找转折点

将单位圆的圆心放在构造曲线上，顺着曲线方向移动.设置圆心角阈值，记录构造曲线和圆心之间的圆心角，若圆心角的度数小于该阈值，则将此时圆心的坐标记录下来，将其视为转折点；Ji若某一段曲线内有数个点符合条件，则只将首尾两个符合要求的点视为转折点而忽略中间的点.与之前得到的T形结点JT、十字交点JX、尖点JX相结合，得到函数图像的特征点集PA.与已有的方法相比，本方法点的数量更少，计算更加便捷.

3.2 寻找构造曲线的互对称关系

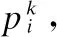
移动对称，即一条封闭曲线可在某一方向上移动一定距离来与另一封闭曲线重合.将每条曲线上的特征点依次连接，计算各连接线的斜率，按特征点的顺序，比较两条连接线的斜率.设置一个阈值范围，若两条连接线的斜率比值在阈值范围内，这两条线可视为相互平行，并调整顶点位置使两条线平行，继续比较下一对连接线.满足第一个条件的两条曲线可进行第二步，将符合第一个条件的曲线上特征点按编号对应连接，设置一个阈值范围，若两条连接线斜率比值在阈值范围内，证明这两条连接线相互平行，同样调整点的位置使两条线平行，继续比较下一对连接线；否则证明这两条曲线不是移动对称的关系.大部分特征点对都符合要求则说明两条曲线互为移动对称(比例可以根据用户的设置修改，默认为80%).遍历满足第一个条件的曲线对，符合第二个条件的即互为移动对称关系.此方法避免了各个特征点连线都平行，但两条曲线不对称的情况，也避免了一个特征点对应另一部分图形的多个特征点的情况.

镜像对称，即一条封闭曲线可通过镜像来与另一封闭曲线重合.将同一组构造曲线上的特征点根据编号依次连接，取两条曲线进行比较，连接两条曲线中p1和p1′、p2和pm′ (m为特征点个数)，比较两条连线的斜率，设定一个阈值范围，若斜率比值在阈值范围之内，取两条连线的中点，连接这两个中点得到对称轴；再连接两条曲线的下一组特征点，将此连接线的斜率与之前连线的斜率相比较，若斜率比值在阈值范围之内，则调整比较点的位置使两条连接线平行.取连接线中点，若该点在刚刚得到的对称轴上，则继续，否则停止，并进行下一对曲线的比较.这两条曲线不对称.遍历所有特征点都符合要求，则证明这两条曲线符合镜像对称条件，此时这一对曲线不再与其它曲线进行镜像对称比较.这样做防止了连线平行但是中点不在对称轴上或连线中点在对称轴上，但连线不平行的情况.

在我们绘制的图像中，有可能存在多条构造曲线互为移动对称的情况.我们使用上述的方法可能会得到多个相互对称的曲线.更特殊的，如果一条曲线既有平移对称关系的曲线，又有镜像对称关系的曲线，则这些的曲线互为对称关系.另外，在这里我们不考虑旋转之后的对称关系.

3.3 寻找自对称的构造曲线

得到互对称曲线后，剩下的曲线中可能存在一部分自对称的曲线.根据3.1得到的特征点，以纵坐标最大的一个特征点为起始点(点p0)，按照曲线的轨迹，逆时针、顺时针方向将曲线上的特征点依次标号(1、-1、2、-2 …)其中逆时针方向为正.自对称曲线的算法与镜像对称的算法类似，得到自对称曲线后剩余的为非对称曲线.

经过以上的步骤，得到互对称曲线对、自对称曲线和非对称曲线.

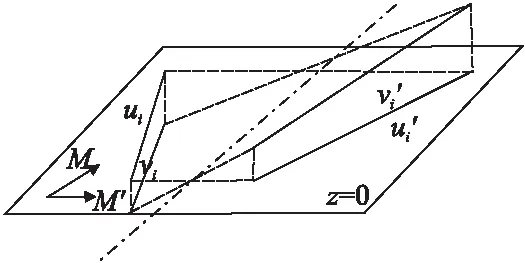
图2 互对称三维坐标计算Fig.2 Mutual symmetric three- dimensional coordinate calculating

4 计算空间坐标

在第3节中，计算了闭合曲线之间的对称关系，这一节要利用对称关系来计算图像在三维空间的位置.在计算对称关系的过程中使用同一个对称平面P.

4.1 互对称关系时的计算

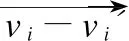
M·(vi+v′i)=0

(1)

M×(vi-vi′)=0

(2)

经过推导得到等式(3)、(4)、(5)、(6).

xM(xi+xi′)+yM(yi+yi′)+zM(zi+zi′)=0

(3)

yM(zi-zi′)-zM(yi-yi′)=0

(4)

zM(xi-xi′)-xM(zi-zi′)=0

(5)

xM(yi-yi′)-yM(xi-xi′)=0

(6)

由于需要计算的是z坐标，而x、y坐标已知，故忽略等式(6)，只保留等式(3)、(4)、(5).根据等式(3)、(4)，推导出zi和zi′：

(7)

(8)

同样也可以根据等式(3)、(5)来推导zi和zi′的值：

(9)

(10)

若点vi和vi′重合，即这两个点位于平面P上，则该点的z坐标如等式(11)所示：

(11)

当且仅当zM不为0，且等式(12)成立时，以上zi值的计算才是可行的.

(12)

其中向量M中zM的赋值，对于建模结果存在影响：较小的zM值使得对称面更接近于竖直，空间中两对称点的距离相对较大；较大的zM值则相反.

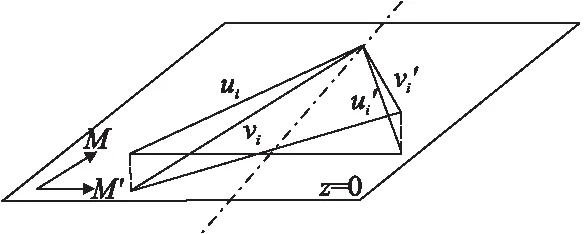
图3 自对称三维坐标计算Fig.3 Self symmetric three- dimensional coordinate calculating

4.2 自对称关系时的计算

在寻找对称关系的计算中，我们已经得到了自对称曲线的对称轴，并将起始特征点设置为点p0,逆时针、顺时针方向上的特征点分别为vj(xj,yj,zj),vj′(xj′,yj′,zj′).与互对称中相似，如图3所示.经过推导，得到zj和zj′的值：

(13)

(14)

同样，若点vj和vj′重合，则该点的z坐标如等式(15)所示：

(15)

当且仅当zM的值不为0，且等式(16)成立时，zj值的计算才是可行的.

(16)

对于没有对称图像的一般曲线，它位于对称平面上，z坐标的计算方式如等式(17)所示：

(17)

5 曲面生成及模型组合

对于每一个特征点，根据第4节得到深度信息得到三维构造曲线.文献[15]等提出的在两条构造曲线的基础上增加一对非对称一般曲线作为构造曲线的方法，模型的每一部分将根据这四条曲线得到.在本文中，参考文献[16]，在两条构造曲线的基础上绘制一对辅助曲线tu，tu的两个端点分别在两条构造曲线上.将tu的两个端点p0(x0,y0,0)pn(xn,yn,0)沿构造曲线的方向移动，特征点坐标定义为：

(18)

(19)

其中，移动前的特征点p坐标为(x,y,0),移动后辅助曲线tu′的两端点坐标分别为p0′(x0′,y0′,0)、pn′(xn′,yn′,0)，特征点坐标为p′(x′,y′,0).根据等式(18)(19)可推导出特征点p的坐标值，当且仅当xn≠x0且yn≠y0时，等式(20)成立.

(20)

此时辅助曲线的特征点和构造曲线位于同一平面.对辅助曲线进行旋转，以p0、pn的连线为轴，旋转辅助曲线得到模型深度信息.设旋转前曲线上点为p(x,y,0)，旋转后曲线上点为p′(x′,y′,z′)，p0、pn的连线为l=f(x,y)，点p到l的最小距离点为pmin，最小距离为d，则点p坐标为：

(21)

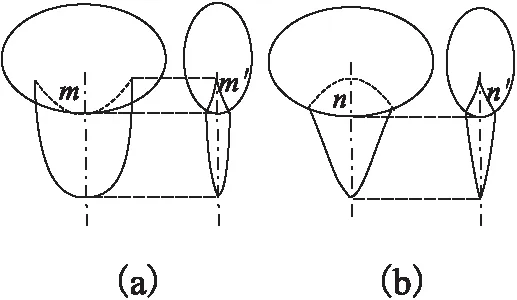
图4 三维模型组合Fig.4 Three-dimensional model combination

以构造曲线为轨迹，将旋转后的辅助曲线进行扫掠创建三维模型.若使用交互计算深度信息，这将增加一个操作步骤.这里依据构造曲线间的深度关系组合三维模型，得到的三维模型是各部分模型的并集.对于两个尖点间的构造曲线，构造曲线I补充曲线的中点m与构造曲线II相接触，如图4(a)所示.对于两个T形结点或者两个十字交点之间的部分构造曲线，以构造曲线I上的点n作为定位点，构造曲线I与构造曲线II创建的三维模型基准平面为同一个，如图4(b)所示.

6 结果与讨论

本文提出的算法在Mac OS系统上利用JavaScript实现.在计算机或移动设备上绘制手绘图形以及辅助曲线，或导入二维图形并绘制辅助曲线(若未绘制辅助曲线，则该部分的横截面按照默认辅助曲线进行三维建模)，完成后将绘制的图像传输到建模软件中，之后建模软件自动建模.

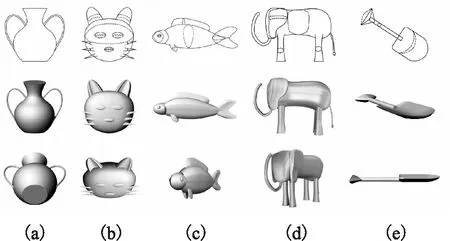
图5 建模案例Fig.5 Case of modeling

为了检验本文方法的易用性，用户了解基本操作之后在设备上绘制图像.图5第一行是用户输入的图形，其中辅助曲线用虚线来表示，所有曲线都在同一平面上；图5第2、3行为计算建模后得到的三维模型不同角度的视图.使用本文中的方法可以构建出Teddy方法生成的模型，只需要将辅助曲线设置成圆形，如图5(a)的模型；图5(b)-图5(e)是用户添加辅助曲线后得到的三维模型.图5(a)中构造曲线为一对互对称曲线(把手)和一条自对称曲线(瓶身)，图5(b)-图5(e)中构造曲线存在互对称曲线、自对称曲线和一般曲线，以图5(c)中的鱼为例，鱼的腹鳍为互对称曲线(另一半腹鳍未画出)，鱼头、鱼身、鱼尾是自对称曲线，背鳍是一般曲线.

值得一提的是，本文使用辅助曲线来控制模型形状，能够生成更复杂、自由度更高的复杂模型，每部分的形状不必受限于规定的横截面形状.以图5(e)的铲子模型为例，图6(b)、(c)、(d)分别是使用文献[7，12]的方法与使用本文的方法构建的模型.与图6(d)所示三维模型相比，图6(b)中所示的模型横截面形状为圆，与用户的构思差距较大；图6(c)增加了一些真实感，然而铲子的铲面没有创建出来.可以看出，本文的方法创建的模型准确度更高，并具有更高的自由度.

该方法仍然存在一些不足.首先，在寻找图形对称关系时依赖图形之间的连接，若图形之间存在不相互连接的情况，组合模型的过程中各部分图形间的位置关系无法确定.其次，对于输入的图像，以模型的主视图或侧视图较为合适.输入图像的视角若过于倾斜，将有可能导致系统在判断构造曲线上特殊点种类以及构造曲线对称关系时得到错误结果，从而使生成的模型出现错位的现象.再次，创建的模型可直接用于对精度要求不那么高的行业，构建模型的尺寸较小，而对那些对高精度要求的行业，如精密机械等，有一定的局限性；同时当绘制的构造曲线比较密集，将导致曲线和交点太过密集，此时建模时间会大大增加，甚至建模失败.

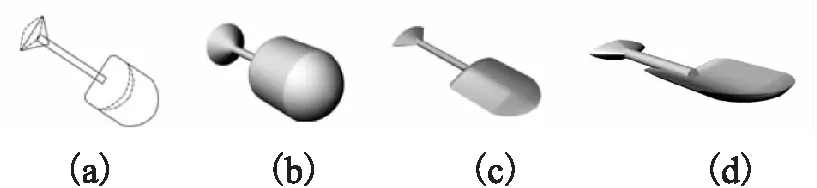
图6 与已有方法比较Fig.6 Compare with existing methods

7 结束语

本文提出了一种基于单幅及其辅助曲线的三维建模方法，本方法通过用户输入图像，根据对称性计算图形在三维空间中的位置，通过辅助曲线控制模型形状，从而实现三维模型的创建.该方法具有算法简单、建模速度快、受环境和设备影响小、实用性强等优点，可广泛应用于教育、游戏等三维模型的设计和加工.针对上述不足之处，下阶段工作中我们将从提高建模精度，同时减少建模所需的时间方面入手，进行进一步的研究和优化.