一种基于改进蜂群算法的网络重构技术

潘成胜,李 金,2,蔡睿妍,2,杨 力,2

1(大连大学 通信与网络实验室,辽宁 大连 116622)2(大连大学 信息工程学院,辽宁 大连 116622)

1 引 言

随着通信技术以及中国航空航天事业的迅猛发展,由海、陆、空所组成的新一代智能一体化通信网络[1,2]框架已逐步形成,作为地面与太空通信的媒介-空间信息网络,将承担大量的信息获取、传送和分发的重任.然而,由于卫星节点的移动性、无线通信的脆弱性以及外太空空间内所存在的不确定性等因素影响,导致卫星网络的通信性能会随着拓扑结构的变化而变化,甚至有可能会因局部节点失效所引起的拓扑分割最终导致通信网络的整体失效.因此,如何动态维持网络拓扑结构的稳定性以及通信的可靠稳定性,成为了国内外研究热点.空间信息网络的拓扑重构问题是一个需要考虑卫星节点间的可见性、可连通时间以及连通度等多约束组合优化问题,其目标是在资源受限的前提下满足链路连通时间和连通度的要求,通过将空间信息网络中具有剩余连通度的卫星节点进行链路选择链接,重构拓扑结构,提高空间信息网络的抗毁性[3,4],保证网络的通信效率.近年来,出现不少针对空间信息网络拓扑重构重构算法研究.文献[5]中通过动态路由的方式检测故障链路,采用传统功率控制方式(Transcation Power Control,TPC)进行链路重构,在节点损坏过少或不集中的情况下采用该算法重构效果颇有成效,但当节点损坏过多或损坏节点较为集中时则容易出现拓扑漏洞,整体重构效率较低.文献[6]中提出一种利用蚁群算法(Ant Colony Algorithm,ACO)完成空间拓扑修复和预测网络链路过载情况的方法,该算法整体效率偏优但存在着收敛时间过慢、易陷入局部最优的缺点.文献[7]中通过遍历选择聚合度较大节点完成链路重构,忽略了节点连通时间,易造成多次拓扑重构,造成资源的浪费.

研究空间信息网络重构问题的关键是在于建立有效的网络模型、确立合适的评价指标,进而设计重构算法,使得空间信息网络拓扑结构能在短时间内完成重构,以满足工程应用需求.本文首先根据空间信息网络的特点确立卫星网络模型及节点模型,然后定义卫星可连通度约束、可连通时间约束和潜在链路发现约束,确立空间信息网络的链路模型,最后确定合适的评价指标以及设计相关约束函数模型,使得该模型以尽可能提高网络的抗毁性为目标.基于所建立的空间信息网络拓扑模型,本文提出一种基于改进人工蜂群算法(Improved Artificial Bee Colony Algorithm,IABC)的节点重构技术.该方法首先将卫星网络中的节点编码,委派身份信息,然后利用蜂群算法对链路进行迭代更新,并以网络效率高低作为为链接是否有效的判据.仿真表明,该算法在优化网络拓扑结构、增强卫星网络抗毁性的基础上,还可以优化提高卫星网络的通信效率.

2 空间信息网络模型

本文所提算法主要解决的是空间信息网络中的卫星网络拓扑重构问题,地面网络拓扑结构相对稳定故不考虑在内,所以该网络模型[8]可简化为:

G={Sat,Link}

(1)

其中,Sat代表空间信息网络中所有的卫星节点的集合,Link表示网络中链路的集合.

2.1 空间信息网络节点模型

对于卫星节点,本文主要考虑其节点编号、卫星节点的连接度以及潜在链路个数,故卫星节点模型可表示为:

Sat={s,degree,latent}

(2)

其中,s表示卫星节点编号(s∈(1,2,…,N));degree为卫星节点的连接度;latent表示此节点存在潜在链路的个数.如果节点间的连接没有度约束限制,完全图具有最优的抗毁性[9],但在空间信息网络的背景下,连接度受节点功率以及卫星自身表面积等因素影响,故该参数是在重构算法设计时所要考虑的重要约束条件之一.潜在链路的发现取决于可见性和链路的连接时间,具体定义如下:

定义1.卫星可见条件:

卫星节点在绕地球做周期性运动的过程中会受到来自地球和大气层的遮挡,所以两颗卫星所形成的链路长度存在一个最大值,即最大可见链路长度.其星间链路长度dAB可表示为公式(3):

(3)

其中,R为地球半径;hA、hB分别为卫星A与卫星B所在的轨道高度;ξ为地心角.但在实际情况中,由于星间链路会受到地球的遮挡,故任意两颗处于不同轨道的卫星在某一时刻,它们的之间的星间链路长度存在一个最大值,即为最大可见链路长度.假定此时卫星A与卫星B之间的链路长度dAB为其最大可见链路长度,可表示为:

(4)

同时,可以推出最大地心角可表示为:

(5)

当两颗卫星间链路长度dAB满足dAB≤dmax,地心角ξ满足ξ≤ξmax时,两颗卫星可见;否则,两颗卫星不可见,即不存在潜在链路.

定义2.链路连接时间:

由于空间信息网络的拓扑具有时变性,所以星间链路在连接和断开两个状态间频繁切换.若要建立稳定的网络结构,则需对星间链路连接时间加以分析.链路连接时间TLink(i,j)是指卫星i和卫星j从建立链路开始,到链路断开的这一段时间.可以用公式表示.

TLink(i,j)=Tend(i,j)-Tstart(i,j)

(6)

其中Tstart(i,j)和Tend(i,j)分别表示卫星i和j之间链路的建立时刻和链路断开的时刻.为了减小星间链路频繁切换,本文定义了最小连接时间Tmin,只有当TLink(i,j)≥Tmin时才具备建立链路的条件.

2.2 空间信息网络链路模型

根据空间信息网络特点,星间链路模型[10]可描述为:

Link={L(i,j),TLink(i,j),l(i,j),C(i,j)}

(7)

其中,L(i,j)表示si星和sj星之间的星间链路,l(i,j)表示此链路的长度,C(i,j)为链路容量.

2.3 评价指标

空间信息网络拓扑G={Sat,Link}是由Sat=N个节点和Link=M条链路所组成.图G中wij表示节点i和j之间的边权值,其中边权值用来表示节点之间信息流通的难易程度,数值越小信息流通越容易,网络传输效率越高.本文定义边权值为两节点之间最短路径上的边数,用d表示.本文中网络效率指标E[11]定义为

(8)

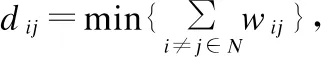
本文中定义移除节点k后网络的鲁棒性为:

(9)

(10)

其中,pk表示节点k被移除的概率.

2.4 问题建模

本文所提出的优化问题可形式化描述为:给定卫星网络拓扑图G(Sat,Link)和正整数q,如何合理的选择有限节点集Sat′,添加有限边集Link′(Link′≤q&& Link′∩Link==φ),使得重构后的拓扑图G′(Sat,Link∪Link′)具有最优可生存性,其中网络生存性用指标Q来衡量,即使Q(G′)取得最大值.

在有限资源的情况下可生存性可描述为:

Max Q(G′(Sat,Link∪Link′))

(11)

s.t. Link′={(u1,v1),(u2,v2),…,(us,vs)}

(11-a)

us,vs∈Sat,us≠vs,(u1,v1)∉Link,s∈[1,N]

(11-b)

degree≤Maxdegree

(11-c)

TLink≥TLimit

(11-d)

dAB≤dmax

(11-f)

ξ≤ξmax

(11-g)

C(i,j)≥Cmin

(11-h)

其中,可生存性指标Q(0≤Q≤1)描述了节点移除对网络通信效率的影响,反映了系统维持通信功能、适应环境变化的能力,在重构链路时必须满足述约束关系式(11-a)-(11-f).

3 基于改进蜂群算法的网络拓扑重构算法

3.1 优化目标及基本思路

为求解空间信息网络拓扑重构问题,本文提出一种基于改进蜂群算法的拓扑重构方法.基本思想是在卫星网络发生节点失效的情况下,以节点最大功率为搜索半径寻找潜在可连通节点,以连可通时间和可连接度为约束条件筛选过滤节点,然后通过蜂群算法迭代出最优节点进行链路连接以完成网络拓扑重构,使重构后的网络具有良好的网络效率和较高的抗毁性.在重构实现过程中,选择适宜节点完成网络拓扑重构有三方面的重构目标.其一,改善卫星网络在随机故障和选择性攻击情况下的网络抗毁性;其二,通过改善网络中节点之间通信状态,提升网络通信效率;其三,延长网络生存时间.

为实现这些目标,本方法实现过程的基本思路如下:

1)改善网络有效性,鉴于选择性攻击中,关键节点及其连接边容易成为目标对象,而连通度较低的节点及连接边更容易生存下来.在本方法中,我们更倾向于优先选择连接那些连通度较低的节点.此外,连接那些连通度较低的节点也能有效地改善网络中度分布的不均匀性,进而改善网络抗毁性.

2)改善网络传输效率,通过选择适宜节点重构,使重构后所形成的网络具有稳定高效的链路通信能力,保证数据稳定传输.

3)节约成本,在选择节点重构时把可连通时间作为一个约束条件,使整个网络的稳定通信时间延长,降低频繁重构所带来的不必要开销.

3.2 人工蜂群算法简介

人工蜂群算法(Artiticial Bee Colony Algorithm,ABC)[12-14]是一种根据蜜蜂采蜜行为所提出的群智启发式迭代算法,其组成要素主要有食物源、引领蜂、跟随蜂和侦察蜂,其中蜜蜂所搜寻的蜜源代表待求解问题的一个可能解,用适用度值的大小来描述该食物源丰富度等相关信息,通过不断更新食物源的位置以及对其周围进行邻域搜寻的方式来更新局部最优解,从而获得全局最优解.ABC算法在求解多约束优化问题方面的应用已较为成熟[15-17].下面阐述运用ABC算法求解空间信息网络拓扑重构问题的具体过程.

3.3 改进的蜂群算法

3.3.1 解的描述

运用ABC算法进行空间网络拓扑重构时,解(x)代表了待重构节点功率可达周围内所有满足约束模型的候选节点,比如:待重构节点周围有N个后选节点,则重构问题的具有N个可能解,每一个解就代表重构时一种链路链接的可能,其适应度的大小代表重构后网络状态情况(计算过程见下3.3.2),该算法所求得使适应度值最大的函数解,即为在当下最优重构方案.

3.3.2 适应度相关表达式

对于一个待求解(x),其适应度计算表达式(即目标函数)为:

(12)

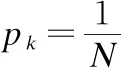
3.3.3 待求解(x)初始化

设置算法种群的规模(N),随机从种群中选取N/2个初始解,依次与待重构卫星节点连接断开测算,并计算各解所对应的适应度值,保留适应度的最大值和最小值最为邻域搜索公式的xmin和xmax变量.

3.3.4 解的邻域寻优

在ABC算法寻找最优食物源的过程中,需要在一个食物源的附近进行搜索更新,确保周围是否存在比当前位置资源更丰富的食物源,将这种行为成为邻域寻优行为,求得的问题解称之为邻域解,在ABC算法中解的邻域操作是一个局部寻优的过程,所以选择一个怎样的邻域更新方式对算法的性能表现具有很大的影响,本文采用等概率随机抽取的方式来对当前食物源进行邻域寻优操作,算法过程如下:取当前解对应的x,将该值经过等概率随机选取函数处理后生成一个邻域节点,即解(xp,xq).本文在进行邻域操作时采用贪心算法来选择较优解,计算比较二者的适应度值(f(xp),f(xq)).如果f(xp)>f(xq),则选择xp,否则选择xq.

3.3.5 最优解xbest

传统的ABC算法存在容易陷入局部最优和后期较慢的问题,为克服该问题本文提出一种引入全局因子的位置更新公式:

Vij=xij+rij(xmj-xkj)+f(xbest,j-xij)

(13)

其中,Vij表示在当前食物源xij进行局部更新搜索所求出的新的待求解食物源位置;k,m∈{1,2,…,N},其中k,m,j都是通过等概率随机选组函数所生成的随机数,k、m和i三者互斥,rij∈[-1,1],xbest,j表示目前所求得的最优问题解.传统蜂群算法在进行局部搜索更新操作时仅仅向着rij(xmj-xkj)所表示的矢量方向搜寻更新,寻找方向受到了限制,并且缺乏两个邻域解之间比较的过程.蜂群寻找最优食物源的过程是一种群体进化的过程,蜂群中每个蜜蜂都可以从其他蜜蜂寻蜜过程中获得进步成长,但是传统的蜂群算法缺乏这方面的考虑,仅仅比较每个蜜蜂每一次的寻蜜过程.所以在原公式的基础上加上了全局引导因子xbest,j-xij,使蜜蜂的搜索行为具有了全局进行性,并且加强改善了方向性.通过加入影响因子φ来控制更新优化行为的大小.从位置更新公式的组成元素可以看出,当前位置和最优位置之间搜索距离大小是动态更新的.而且,为了避免算法在更新过程中发生丢弃局部最优解的情况,用一个局部变量lm来保存迭代过程中产生的最优重构方式,用xbest,j来保存全局最优解,该解对应的重构方案即为全局最优重构连接方案.

3.4 算法步骤

利用改进蜂群算法对卫星网络进行拓扑重构的步骤如下:

1)当网络拓扑中发生节点失效的情况时,网络局部链路的时延会急剧上升.将涉及链路的节点编号为s(s=1…N),开始以Rmax(Rmax=k·Tmax·v均值,其中k为调节系数,v为网络中节点可移动速度的平均值,Tmax最大可工作时间)为半径搜索区域内可达节点,并以链接条件为约束(星间链路长度小于最大链路长度,星间链路链接时间大于最短链接时间),确立编号为1的种群规模ms,最大迭代次数Lmax,初始化ls用于记录遍历次数,令全局变量v=1.依次建立剩余编号卫星的待求解节点集合,直到所有节点遍历完成.

4)xbest即为本次算法得到的最优解,对应的链路连接即为本次重构最优链路选择.

5)分别以编号为2-n的卫星节点为初始节点,重复Step1.

6)根据Step 3的结果,如果存在卫星节点维持的星间链路数目大于4条的情况,则需要删除多余的星间 链路.删除链路的依据是在卫星节点的整体可达性不变的情况下删除被选择概率p最小的链路.如果存在两条可删除的被选择概率相同,则删除节点剩余连通时间较小的链路.如果一个卫星节点存在的链路数目小于4,则建立被选择概率最大的链路,以确保任意两个卫星节点间的星间链路的数目均等于卫星节点的度,退出程序.

4 仿真分析

4.1 仿真平台与仿真环境

本文所采用的仿真软件为ONE1.5和STK,虽然ONE1.5仿真软件对于DTN网络具有良好的支持性,但其不支持卫星网络.所以需要先通过STK软件获取当前卫星网络节点分布及链路链接情况,导出并降维成二维直角坐标系上的数据,然后在OpenJUMP中进行编辑定义处理,最后,显示出相关仿真结果.

本文所选卫星模型为铱星网络模型,具体在参数如表1所示.

综合考虑卫星网络的连通性、系统成本以及卫星处理能力等因素,本文选取的卫星节点的最大连接度等于4.

4.2 算法重构时间仿真

由图1中可以看出,ACO算法的收敛时间要高于其余两种算法,其主要原因是传统的ACO算法虽然具有良好的探索能力,但开发能力不足,在算法初期,由于链路上缺乏信息素引导,只能随机的选择下一节点连接, 故收敛时间较长.ABC算法通过迭代完成卫星的网络重构,但随着卫星个数的增多,其操作所需的时间增多,并且易陷入局部最优解,导致重构时间较长.本文所提出的IABC算法利用改变初始节点选取以及节点信息增量的方法,减少了算法的收敛时间,进而优化了整个网络的重构时间.

图1 重构时间仿真Fig.1 Reconstruction time simulation

表1 卫星网络仿真参数Table 1 Satellite network simulation parameters

4.3 算法效率仿真

从图2中可以看出,TPC算法分组投递率会随着损坏节点的数量增多而减小,这是由于当节点损坏较多时,单纯的通过功率调节无法完成拓扑的重构,易产生拓扑漏洞,导致网络整体效率降低;ACO算法当节点损坏较少时网络效率可以接受,当节点损坏超过一定数目时,选择节点时易陷入局部最优解问题,导致网络效率下降.IABC算法根据筛选条件可过滤掉差、劣节点,使重构选择节点时让网络效率大体上维持一个高位值.

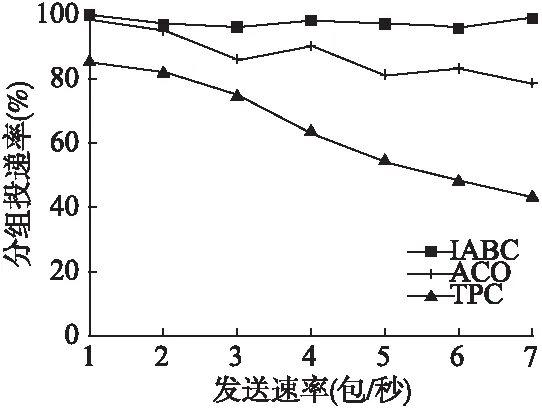
图2 网络效率仿真Fig.2 Network efficiency simulation

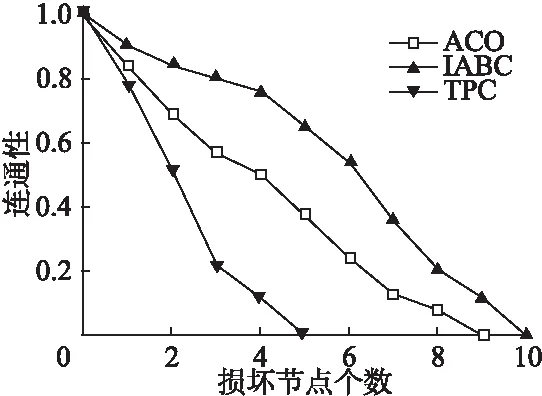
图3 网络抗毁性仿真Fig.3 Network survivability simulation

4.4 算法抗毁性仿真

从图3中可以可以出随着节点损坏个数的增多,网络的连通性不断减少,最后网络彻底失效,但通过对三个方法的仿真比较可以看出:在进行重构后,本文所提出的算法其网络连通性要明显高于其他两个算法,而且可以看出当损坏节点在六个以内该算法所重构后的网络具有较强的连通性,延长了网络的生存时间.

5 结 论

本文针对传统蜂群算法收敛速度慢的特点,改进了蜂群算法,并将其应用到卫星网络拓扑重构中,提出IABC.仿真结果表明,本文的算法在收敛速度上有着很大的优势,并且有效的提高了卫星网络拓扑的稳定性.下一步的工作,我们将会继续优化蜂群算法,使其收敛时间减小,并且与遗传算法相结合,解决多态卫星网络重构问题.