一种基于邻域容差信息熵的组合度量方法

姚 晟,陈 菊,吴照玉

(安徽大学 计算机科学与技术学院,合肥 230601) (安徽大学 计算机智能与信号处理教育部重点实验室,合肥 230601)

1 引 言

粗糙集理论[1]是由波兰学者Pawlak提出的一种处理不确定性数据的数学工具.目前,粗糙集理论已经广泛应用于模式识别和机器学习等诸多领域中[2-5].不确定性度量是粗糙集理论的重点研究内容.经典粗糙集采用的精度、粗糙度、近似精度以及近似粗糙度[6]进行不确定性度量,这些方法归纳起来都是运用粗糙集的边界域来描述信息系统的不确定性,最近的研究表明,这种度量方式仍存在一定的不足[6].为了解决这一问题,近年来,一些学者也从其它视角提出了一些改进的不确定性度量方法.例如粗糙熵[7]、信息熵[8]、知识粒度[9]等,这些新度量方法的提出使得信息系统的不确定性度量的研究逐渐趋于完善.

经典粗糙集理论建立在等价关系基础之上,所以它只适合处理符号型数据.由于目前的信息化时代发展速度之快,数值型数据已普遍存在于各个领域,经典粗糙集在处理数值型数据时,它需要将数值型数据进行离散化处理,这难免会造成一些重要的数据丢失.接着,Lin[10]所提出的邻域粗糙集模型解决了上面的问题,因为邻域粗糙集可以直接有效的处理数值型数据,近几年来就其不确定性度量方法已经得到许多学者和专家的研究.Chen等学者[11]在邻域信息系统中定义了邻域熵的概念,并能够有效的处理数值型信息系统的不确定性度量问题.而现实生活中,大量存在着不完备数据或者混合型不完备数据,然而,上面所说的方法仅能够处理完备的数值型数据.因此,针对如何处理不完备数据或者混合不完备数据已经成为目前研究的热点[12].Wang等学者[13]提出了基于数据驱动量化容差关系的扩展粗糙集模型,该模型可以用来处理离散型不完备的数据,但不能够处理数值型数据.针对这一问题,姚晟等学者[14]提出了基于邻域量化容差关系的粗糙集模型,该模型能够有效的处理数值型不完备的数据,但是该模型不能够处理离散型不完备的数据.何松华等学者[15]提出了邻域组合测度,该度量方法可以有效处理混合数据,然而该度量方法在设置对象与对象之间的距离时,当某个对象所对应的属性值为缺失值时,则此对象与任一对象之间的距离就设置为0,该距离的设定不太严谨,仍存在缺陷,因为他们并没有实实在在的考虑到信息系统中数据自身分布情况和潜藏在其中的知识.

针对上面的问题,本文构造了一种改进的不完备邻域粗糙集模型,该模型主要利用统计学的方法求出已知属性值的频率,将该频率作为该属性值的概率,相比之下这种方法更加严谨和客观,因为考虑了数据的自身分布情况.在该模型之上,本文首先定义了混合近似精度和混合近似粗糙度的概念,接着考虑到近似精度和近似粗糙度对信息系统的不确定度量上存有缺陷[6].为了解决这一缺陷,将进一步引入邻域容差信息熵的概念及相关性质;最后提出一种基于邻域容差信息熵的组合度量方法,并且研究了相关性质.实验结果表明,本文所提出的方法具有一定的度量效果,验证了该方法具有一定的优越性,并且从理论上也证明了该方法的可行性.

2 不完备邻域粗糙集模型

2.1 邻域容差关系

定义1[16].设不完备信息系统为IIS=(U,C,V,f),其中B⊆C,B=BN∪BS,BN表示的是数值型属性集,BS表示的是符号型属性集,δ是一个非负数值,则关于混合属性集B的邻域容差关系定义为:

b(x)=*∨b(y)=*∨((b∈BN,Db(x,y)≤δ)

∧(b∈BS,Db(x,y)=0))}

显而易见,邻域容差关系满足自反性、对称性,但是不满足传递性.尤其,当这里的属性值全部为符号型属性时,邻域容差系就退化为容差关系.

2.2 邻域容差类

由邻域容差关系可知它满足以下几个性质:

性质1[16].设不完备信息系统为IIS=(U,C,V,f),δ为一个非负数值,B⊆C,则满足:

性质2[16].设不完备信息系统为IIS=(U,C,V,f),δ为一个非负数值,且B2⊆B1⊆C,则满足:

性质3[16].设不完备信息系统为IIS=(U,C,V,f),B⊆C且δ1,δ2为两个非负数值,且满足δ1≤δ2,则满足:

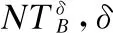
定义4.设不完备决策信息系统为IDIS=(U,C∪D,V,f),混合属性子集B⊆C,δ为一个非负数值,且决策属性D的等价类划分为U/D={D1,D2,…,Dm},则U/D关于B的混合近似精度和混合近似粗糙度分别定义为:

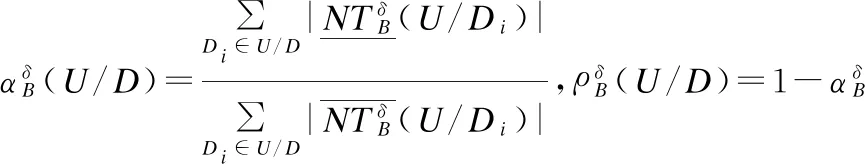
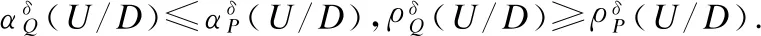
证明:此处省略证明.

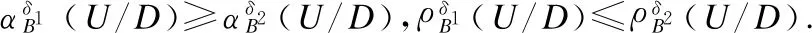
证明:此处省略证明.

3 基于邻域容差信息熵的组合度量

3.1 邻域容差信息熵

粒结构模型[17]是粒计算理论中的一种重要表现形式,并且可以作为衡量信息系统分类能力的一种有效方法,它是将论域中每个对象都粒化入一个信息粒中.目前,该方法已经被众多学者所运用,并相继提出了多种粒结构模型[18].本文在此基础上,提出了基于邻域容差关系的粒结构模型.

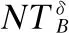
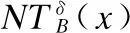
Shannon的信息论[19]为用熵度量数据集的信息提供了一种可行的方法.熵可以作为信息系统的不确定性度量.如果最初只给出关于类的概率知识,那么与信息系统相关的不确定性就可以用熵来进行度量.作为一种重要的不确定性度量,信息熵及其变形已经得到了深入的研究.Liang等学者们[20]在不完备决策信息系统中提出了了一种新的信息熵.本文,我们将Liang[20]提出新的信息熵推广到邻域容差粒结构模型中,提出了一种新的信息熵,即邻域容差信息熵,并且研究了相关性质.

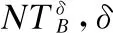
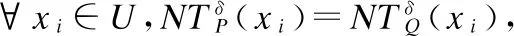
性质8(单调性).设不完备信息系统IIS=(U,C,V,f),δ为一个非负数值,若Q⊆P⊆C,则邻域容差信息熵满足NTHδ(Q)≥NTHδ(P).

证明:

这段颇为得体而诚恳的回答，给子女的铺张敲响了一记警钟，祁氏一门作为遗民表率，时时有大祸临头的危险，何况她的儿子还在进行着反清的活动。商景兰对此有着清醒的认识：富贵不可倚赖，惟有“清标”之行，可以不朽。因此后来祁家破败潦倒，但“清标”之行却永载史册。末句不仅是对子女的教诲，也是商景兰自身生命观的表白。经历故国沦亡、家庭破败，商景兰挺过了作为遗民大家庭的首领的种种压力，她的自我意识也随着岁月的磨砺而凸现，形成独立不迁的品格与气魄。

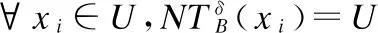
证明:由性质8的证明过程很容易得到该结果.

3.2 组合度量

由定义4可知,混合近似精度和混合近似粗糙度均可作为信息系统的不确定性评估方法.但是,它们是通过近似空间的边界域大小来评估信息系统的不确定性,这种方法对度量信息系统的不确定性要求不够严格[6],为了解决这个问题,本文将融合混合近似粗糙度和邻域容差信息熵各自的优点,提出了一种组合度量方法,并研究了相关性质.

性质10.设不完备决策信息系统IDIS=(U,C∪D,V,f),δ是一个非负数值,若混合子集Q⊆P⊆C,则组合度量满足CMMδ(Q)≥CMMδ(P).

性质11.设不完备决策信息系统IDIS=(U,C∪D,V,f),混合属性子集B⊆C,δ1,δ2是两个非负数值,若δ1≤δ2时,则组合度量满足CMMδ1(B)≤CMMδ2(B).

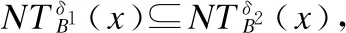
4 实验分析

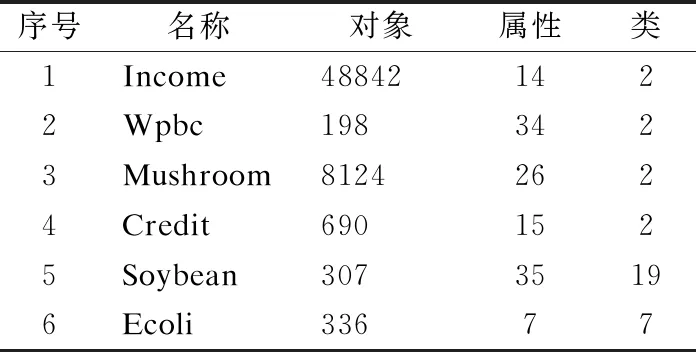
为了验证本文所提出的不确定度量方法具有一定的优越性,本文将从UCI机器学习数据库中获取6个数据集进行实验,每个数据集的具体信息如表1所示.

表1 UCI数据集
Table 1 UCI data sets

序号名称对象属性类1Income488421422Wpbc1983423Mushroom81242624Credit6901525Soybean30735196Ecoli33677

本文通过6组对比实验来验证本文所提出的不确定性度量方法具有一定的优越性.首先将混合近似粗糙度、邻域容差信息熵、和组合度量这三种度量方法分别作用在6组数据集中,然后讨论这三种度量方法随着属性数目的逐渐增加,不确定性度量值的变化情况.本文通过大量实验得出当邻域半径δ∈[0.1,0.2]时,所得实验结果比较好,因此本文实验将选择邻域半径δ=0.15.

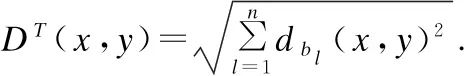
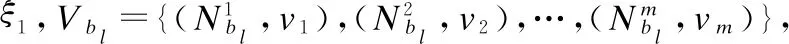
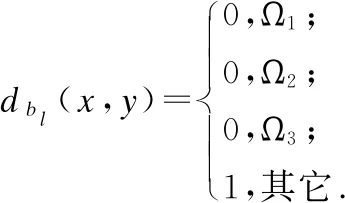
其中:

Ω1=(bl(x)=bl(y)∧bl(x)≠*∧bl(y)≠*);

∨(bl(x)=vi∧bl(y)=*)));

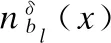
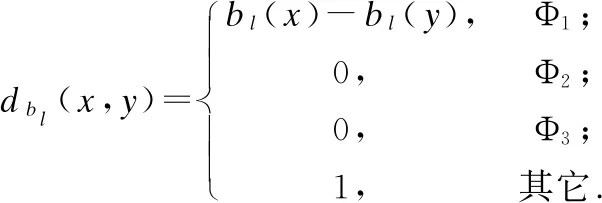
其中:

Φ1=(bl(x)≠*∧bl(y)≠*);

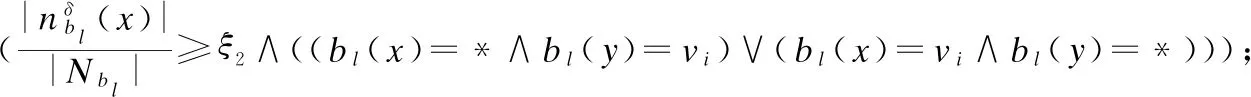
本文实验中所涉及的两个参数ξ1,ξ2,为了更好的获取实验结果,本实验将ξ1,ξ2分别取值为0.5,0.25.

为了方便计算数据集中对象之间的距离,本文将数值型属性按照公式bl(x)=|bl(x)-bl(x)min|/(bl(x)max-bl(x)min)进行标准化处理.三种度量方法在6个数据集上的实验结果如图1-图6所示.

观察图1-图6可以发现混合近似粗糙度、邻域容差信息熵和组合度量这三种度量方法均能够度量信息系统的不确定性.但是本文所提出的组合度量方法比混合近似粗糙度和邻域容差信息熵这两种单一的评估方法更加有效.例如,观察图1可知,在混合近似粗糙度方法中,当属性数目从1增加到3和属性数目从10增加到13时,其不确定性度量值基本上没发生变化,这说明随着知识空间的变化,信息系统的不确定性度量值并未发生改变,与之类似的还有图2-图6.观察图2可知,在邻域容差信息熵方法中,当属性数目从16增加到18时,其不确定性度量值变化较小.观察图5可知,在邻域容差信息熵方法中,当属性数目从20增加到22时,其不确定性度量值基本上没有改变.观察图1-图6可以发现,本文所提出的组合度量方法,其不确定性度量值会随着属性数目的不断增加而单调减小.因此,综合图1-图6可以发现, 本文所提出的度量方法,即组合度量方法在信息系统的不确定性度量方面具有更好的度量效果.

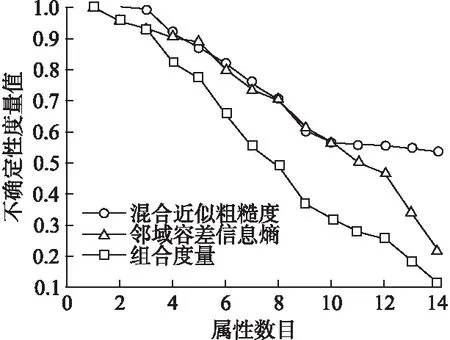
图1 三种方法在数据集Income 实验结果比较Fig.1 Comparison of 3 methods in data set Income experimental results

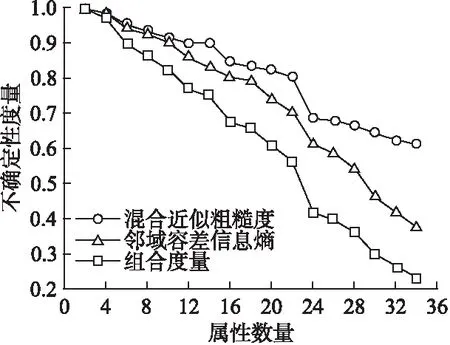
图2 三种方法在数据集Wpbc 实验结果比较Fig.2 Comparison of 3 methods in data set wpbc experimental results

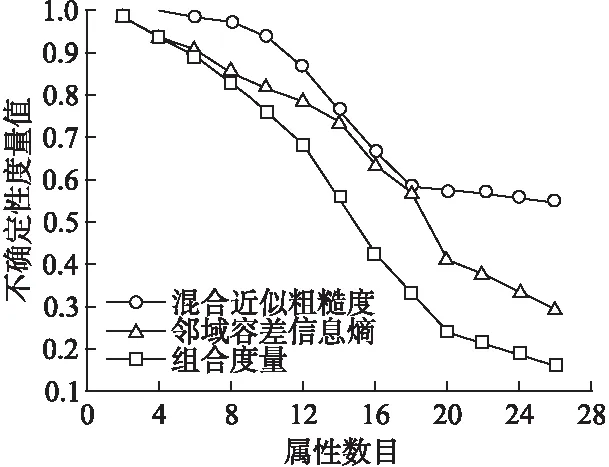
图3 三种方法在数据集Mushroom 实验结果比较Fig.3 Comparison of 3 methods in data set mushroom experimental results

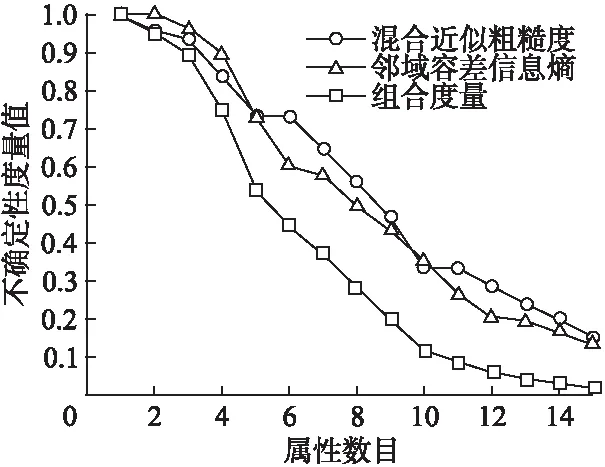
图4 三种方法在数据集Credit 实验结果比较Fig.4 Comparison of 3 methods in data set credit experimental results

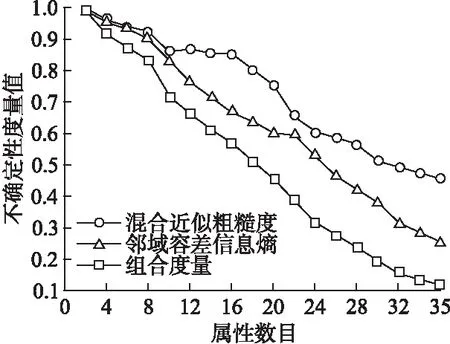
图5 三种方法在数据集Sybean 实验结果比较Fig.5 Comparison of 3 methods in data set sybean experimental results

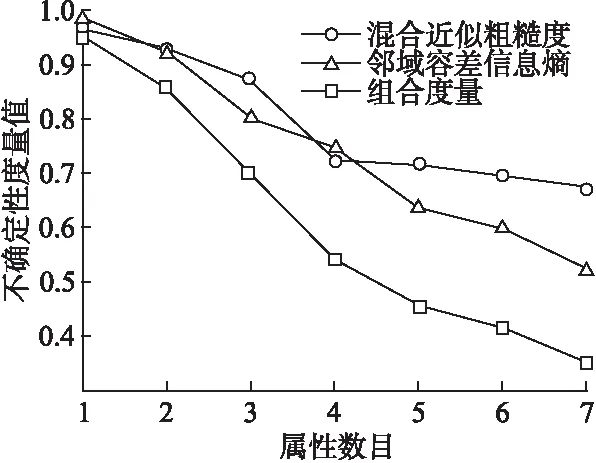
图6 三种方法在数据集Ecoli 实验结果比较Fig.6 Comparison of 3 methods in data set ecoli experimental results

综合上述实验结果分析可以看出混合近似粗糙度、邻域容差信息熵对信息系统都具有一定的不确定性评估效果,但有时并不能够严格地反映信息系统的不确定性,为了克服这两个单一度量方法所存在的缺陷,本文将两种单一度量方法进行了结合,并且实验结果表明该方法具有更好的不确定性度量效果. 因此,综合分析可以得出,本文所提出的组合度量方法对信息系统的不确定性度量具有一定的优越性并且具有一定的合理性.

5 结 语

为了体现多种不确定性度量方法的优越性,本文通过融合混合邻域近似粗糙度和邻域容差信息熵这两种单一度量方法,提出一种组合度量方法.本文提出的不确性度量方法可以作为混合信息系统属性的评估方法,因此接下来可以进一步构建出相应的属性约简方法.