一道2020年新高考Ⅱ卷圆锥曲线解答题的探究及探源

罗文军

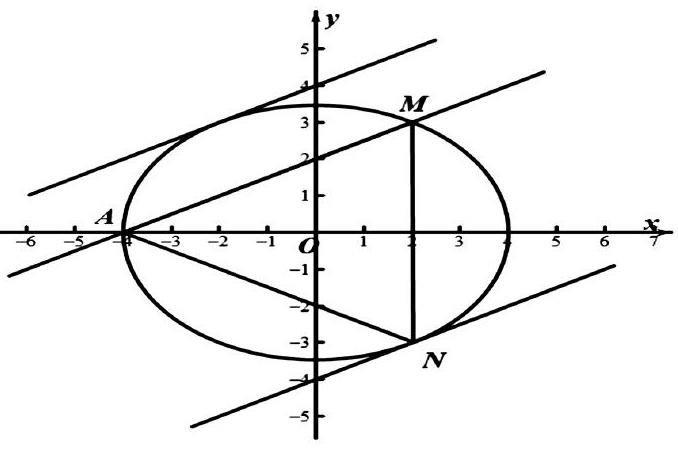
2020年新高考Ⅱ卷解答题的21题是一道圆锥曲线试题，考查了椭圆的定义、几何性质、直线与椭圆的位置关系和椭圆的定值问题，考查了函数与方程思想、数形结合思想，考查了运算求解能力和推理论证能力，旨在考查数学运算、逻辑推理和直观想象的数学学科核心素养，两问之间具有很好的梯度性，第（1）问较简单，第（2）问难度较大，具有很好的区分度，便于高校选拔优秀人才. 以下对这道试题进行解法探究、变式探究和源头探究.

一、真题再现

21. 已知椭圆C：■+■=1（a>b>0）过点M（2， 3），点A为其左顶点，且AM的斜率为■，

（1）求C的方程;

（2）点N为椭圆上任意一点，求△AMN的面积的最大值.

二、解法探究

【分析】（1）由题意分别求得a， b的值即可确定椭圆方程.

【解析】（1）由题意可知直线AM的方程为：y-3=■（x-2），即x-2y=-4.

当y=0时，解得x=-4，所以a=4，

椭圆C：■+■=1（a>b>0）过点M（2， 3），可得■+■=1，

解得b2 =12.

所以C的方程：■+■=1.

（2）【分析1】首先利用几何关系找到三角形面积最大时点N的位置，然后联立直线方程与椭圆方程，结合判别式确定点N到直线AM的距离即可求得三角形面积的最大值.

【解法1】设与直线AM平行的直线方程为：x-2y= m，

如图所示，当直线与椭圆相切时，与AM距离比较远的直线与椭圆的切点为N，此时△AMN的面积取得最大值.

联立直线方程x-2y= m与椭圆方程■+■=1，

可得：3（m+2y）2 +4y2 =48，

化简可得：16y2+12my+3m2 -48=0.

所以？驻=144m2 -4×16（3m2 -48）=0，即m2=64，解得m=±8，

与AM距离比较远的直线方程：x-2y= 8，

直线AM方程为：x-2y= -4，

点N到直线AM的距离即两平行线之间的距离，

利用平行线之间的距离公式可得：d=■+■，

由两点之间距离公式可得 |AM|=■=3■.

所以△AMN的面积的最大值：■×3■×■=18.

【分析2】借助椭圆■+■=1（a>b>0）的参数方程x=acos？渍y=bsin？渍（其中？渍为参数），设出点N的坐标，化为三角函数最值问题，利用辅助角公式求椭圆上的点N到椭圆的弦AM的最大距离.

【解法2】由第（1）问解答过程可知直线AM的方程为x-2y+4=0，椭圆■+■=1的参数方程为x=4cos？琢，y=2■sin？琢（其中？琢为参数），

设点N的坐标为（4cos？兹， 2■sin？兹），由点到直线距离公式可得，

点N到直线AM的距离为d=■=

=■=■，當cos（？兹+■）=1时，即？兹=■时，

d取得最大值dmax=■，

由（1）可知N（-4， 0），由两点间距离公式可得|AM|=3■，

所以△AMN的面积最大值为（S△AMN）max=■|AM|dmax=■×  3■×■=18.

【分析3】利用伸缩变换？渍：x′=？姿·x（x>0）y′=？滋·y（y>0）的性质解答，在变化？渍下，n边形A1A2A3…An（n≥3且n∈N？鄢）变为n边形A1′A2′A3′…An′（n≥3且n∈N？鄢），变换前后图形的面积之比为■=■.

【解法3】在伸缩变换？渍：x′=■x，y′=■y下，椭圆C：■+■=1对应圆O′：x′2+y′2=1，椭圆C上的点A，M，N分别对应圆O′上的点A′，M′，N′，

因为直线AM的方程为x-2y+4=0，所以直线A′M′的方程为x′-■y′+1=0，

圆心O′到直线A′M′的距离为d=■=■，

圆上O′的点N′到圆O′的弦A′M′的最大距离为h=d+r=■+1=■，

|A′M′|=2■=2■=■，

所以△A′M′N′的最大面积为（S△A′M′N′）max=■|A′M′|d=■×■×■=■，

由伸缩变换性质可得，△AMN的最大面积为（S△AMN）max=■=■=18.

【评注】解决直线与椭圆的综合问题时，要注意：

（1）注意观察应用题设中的每一个条件，明确确定直线、椭圆的条件;

（2）强化有关直线与椭圆联立得出一元二次方程后的运算能力，重视根与系数之间的关系、弦长、斜率、三角形的面积等问题.

（3）涉及椭圆的圆锥曲线问题，可以考虑参数方程法和极坐标法.

三、变式探究

变式1 已知△ABC为椭圆■+■=1的内接三角形，且AB过点P（1， 0），则△ABC的面积的最大值为____________.

【解析】经过伸缩变换x′=■，y′=■，得△A′B′C′内接于单位圆x′2+y′2=1，A′B′过点P′（■， 0），

S△ABC=6S△A′B′C′，设坐标原点O′（0， 0）距A′B′的距离为t，则0≤t≤■，|A′B′|=2■，

S△A′B′C′≤■·（1+t），当t=■时，S△A′B′C′有最大值为■，所以S△ABC的最大值为■.

【评注】本题也是求椭圆的内接三角形的面积的最值问题，运用伸缩变换法，结合伸缩变换的性质，将椭圆的内接△ABC的面积的最大值问题化归为单位圆的内接△A′B′C′的面积的最大值问题.

变式2. 已知椭圆C：■+■=1（a>b>0）的一个顶点为A（2， 0），离心率为■. 直线y= k（x-1）与椭圆C交于不同的两点M，N.

（1）求椭圆C的方程;

（2）求△AMN面积的最大值.

【解析】（1）由题意得，a=2，■=■a2=b2+c2，，解得b=■，

所以椭圆C的方程为■+■=1.

（2）解法1：由y= k（x-1），■+■=1联立消去y可得，

（1+2k2）x2-4k2x+2k2-4=0，

△=16k4-4（1+2k2）（2k2-4）=24k2+16>0，

设M（x1， y1），N（x2， y2），由根与系数关系可得，

x1+x2=■，x1x2=■，

由弦长公式可得，|MN|=■

=■=■，

由点到直线距离公式可得，点A（2， 0）到直线y= k（x-1）的距离d=■，

所以△AMN的面积为S=■|MN|d=■=■，

设t=1+2k2，则k2=■，

则S（t）=■，（t≥1），

S（t）=■=■，（0< t ≤1），

所以当■=1时，S取得最大值■.

【评注】本题与前面真题相比，第（2）问也是求与椭圆有关的三角形的面积的最值问题，不同点在本题最后运用了换元法，利用了二次函数的性质求出了△AMN的面积的最值.

变式3. 平面直角坐标系xOy中，过椭圆C：■+■=1（a>b>0）的左焦点的直线x+y+■= 0交于A，B两点，P为AB的中点，且OP的斜率为■.

（1）求C的方程;

（2）M，N为C上的两点，若四边形AMBN的对角线MN⊥AB，求四边形AMBN面积的最大值.

【解析】（1）设A（x1， y1），B（x2， y2），P（x0 ， y0），

则■+■=1，■+■=1，■=-1，

由此可得■=-■=1，

因为x1+x2=2x0，y1+y2=2y0，■=■，

所以a2=2b2，

又由题意知，C的左焦点为（-■， 0），故a2-b2=2，所以a2=4，b2=2，

所以的方程为■+■=1.

（2）由x+y+■= 0，■+■=1联立可得，3x2+4■x=0，

解得x1=- ■，y1=■，x2= 0，y2=-■，

因此 |AB|=■，

由题意可设直线MN的方程为y=x+t，

因为点A，B在直线MN的两侧，所以（- ■-■+t）（■+t）<0，

所以-■< t <■，设M（x3， y3），N（x4， y4），

由y=x+t，■+■=1，消去y可得，3x2+4tx+2t2-4=0，

x3， 4=■，

由弦长公式可得，|MN|=■|x3-x4|=■|■|=■■，

由已知四边形AMBN的面积S=■|MN||AB|=■■，

当t=0时，S取得最大值，最大值为■，

所以四边形AMBN的面积的最大值为■.

【评注】与前文真题相比较，本题第（2）也是椭圆的最值问题，不同在于本题第（2）问是椭圆的对角线互相垂直的内接四边形面积最值问题，最后运用了二次函数值域求出了四边形AMBN的面积的最大值.

变式4. 已知椭圆？祝：■+■=1（a>b>0）的左、右焦点分别为F1，F2，椭圆？祝的四个顶点恰好构成了一个边长■为且面积为2■的菱形.

（1）求椭圆？祝的标准方程;

（2）已知直线l1，l2 均过点F2，且直线l1，l2 的斜率的乘积为-■，设直线l1，l2 与椭圆？祝分别交于点A，B和点C，D，线段AB的中点为M，线段CD的中点为N，求△OMN（O为坐标原点）面积的最大值.

【解析】（1）因为椭圆？祝的四个顶点恰好构成了一个边长为■且面积为2■的菱形，

所以■×2a×2a=2■，a2+b2=（■）2，解得a= ■，b=1，（2分）

所以椭圆？祝的标准方程为■+y2=1.（4分）

（2）设直线l1的方程为y=k（x-1），A（x1， y1），B（x2， y2），

将y=k（x-1）代入■+y2=1，消去y可得（1+2k2）x2-4k2x+2k2-2=0，所以x1+x2=■，

因为线段AB的中点为M，所以xM =■=■，yM =■，（6分）

因为直线l1，l2的斜率的乘积为-■，所以直线l2的方程为y=-■（x-1），（7分）

同理可得xN =■，yN =■，

所以M（■， ■），N（■， ■），（9分）

设线段MN的中点为T，则T（■， 0），

所以S△OMN=■|OT||yM-yN |=■|■|=■×■=■×■≤■，（11分）

当且仅当2|k|=■，即k=±■时取等号，

所以△OMN面积的最大值为■.

【评注】本题第（2）问也涉及到椭圆中的三角形面积最值问题，最后把△OMN的面积用k表示，再运用基本不等式可得求解.

三、源头探究

以下对前文真题进行源头探究.

2020年新高考Ⅱ卷解答题的21题可以看成改编自2014年全国Ⅰ卷理科第20题：已知点A（2， 0），椭圆E：■+■=1（a>b>0）的离心率为■，F是椭圆的焦点，直线AF的斜率为■，O为坐标原点.

（1）求E的方程;

（2）设过点A的直线l與E相交于P，Q两点，当△OPQ的面积最大时，求l的方程.

四、备考建议

在高三一轮复习和二轮复习中，要打破画地为牢，将坐标系与参数方程部分和圆与圆锥曲线部分的复习放在一起作为一个体系. 考生要尝试运用一题多解，例如运用坐标系与参数方程中的参数方程法和伸缩变化法破解椭圆的最值、定值和定点问题，将极坐标方程化为直角坐标方程解答，将参数方程消参后化为普通方程解答，通过伸缩变化将椭圆问题化为关于圆的问题.通过这部分复习，要熟练运用函数与方程思想、化归与转化思想和数形结合思想，提高运算求解能力和推理论证能力，提升数学运算、逻辑推理和直观想象的数学学科核心素养.

责任编辑 徐国坚