基于流固耦合作用的纤维增强复合材料海洋立管涡激振动的三维计算流体动力学模拟

2

(1. 山东理工大学 建筑工程学院， 山东 淄博 255000； 2. 理海大学 P. C. Rossin工程与应用科学学院， 美国 伯利恒 18015；3. 伊利诺伊大学厄巴纳 -香槟分校 土木与环境工程学院， 美国 香槟市 61801)

海洋立管是海洋石油工程中油气开采和输送系统的必备结构。目前，大部分海洋立管由金属制成，随着水深的增加，金属立管的自重导致其对顶张力的要求不断提高，因此需要更大的平台或减少所连接立管的数量，限制了海洋工程向更深海域发展。纤维复合材料具有极佳的机械性能和低密度特点，用其代替传统的金属材料将大幅减小海洋立管的自重，并相应减少对现有海洋平台的顶张力需求和运营成本，也有利于更深海域的油气开发和输送[1]。同时，纤维复合材料有更好的耐腐蚀性、保温隔热性和抗疲劳性，从而可以减少维护方面的成本[2]。纤维复合材料在海洋立管中的应用研究起源于20世纪80年代的法国石油研究所(IFP)[3]，研究表明，复合材料立管是有效和可行的。

涡激振动(VIV)将导致立管疲劳破坏，不仅影响工程进展，而且会产生严重环境灾害，因此各国学者对此进行大量研究，建立了很多VIV模型。VIV研究始于风洞实验[4]，而传统材料海洋立管的VIV实验也在水槽中得以完成[5-6]；此外，各国学者还提出和改进了各种经验模型，以分析立管的VIV现象[7-8]。近年来，计算流体动力学(CFD)技术开始广泛应用于解决VIV问题。纤维复合材料海洋立管作为一种新的海洋立管形式，其VIV特征是一个不可忽略的研究环节。相对于传统金属立管，复合材料立管的VIV研究还处于起步阶段。复合材料海洋立管的结构复杂性和设计参数的多样性，大幅提高了其动力特征研究的难度。Li等[9]利用数值法与解析法结合的方式，探索了纤维复合材料管线的非线性及后屈曲振动特性。Tan等[10]研究了纤维复合材料海洋立管与钢制立管VIV作用下的激励模态、变形的区别。Huang[11]、 Chen等[12]利用工程模拟有限元软件ABQUS与Shear 7软件对比了传统金属立管和复合海洋立管的动力特性。以上研究大多采用经验模型，而流固耦合作用以及纤维复合材料海洋立管的结构构造与每个纤维层的特征没有涉及。

本文中通过等效弹性模量法构建正交式纤维复合材料海洋立管(立管1)、 优化后的纤维复合材料海洋立管(立管2)和金属海洋立管(立管3)； 同时采用层状结构法构建立管1、 2的立管模型。通过基于流固耦合作用的三维CFD的VIV模拟，探索纤维复合材料海洋立管与传统金属海洋立管VIV特征的典型区别，并利用层状结构法模型展示每个纤维层的应力与应变特征。

1 数值模型

1.1 结构构造及材料属性

复合材料海洋立管截面构造参考已有的研究结果[13]， 采用AS4-PEEK型高强碳纤维和材料为聚醚醚酮(PEEK)的内管组成， 分别为22层的立管1 [liner/90/(0/90)10](由内至外分别为内管层、环向增强层、 轴向增强层；liner为内管，90代表角度为90°的环向纤维增强层，0代表角度为0°的轴向纤维增强层，下标10为环向与轴向各层重复次数)与18层的立管2 [liner/03/(+52,-52)5/904](由内至外分别为内管层、 轴向纤维增强层、有角度的纤维增强层、环向纤维增强层；52代表角度为52°的纤维增强层，下标3、 5、 4为各层重复次数)。2种纤维增强复合材料海洋立管及金属立管(立管3)3种海洋立管的尺寸特征如表1所示。

利用等效弹性模量法建立纤维复合材料海洋立管时，所利用的公式[14]为

表1 纤维复合材料海洋立管几何尺寸及密度

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

表2所示为由式(1)—(8)计算所得纤维复合材料海洋立管的等效材料属性。在采用层状结构法建立纤维复合材料海洋立管时，直接采用PEEK内管及单层AS4-PEEK型纤维层的材料属性(见表2)。

1.2 数值模型

采用Fluent软件建立10D×20D的流体场模型，其中D为海洋立管外径，即立管1的尺寸为3.26 m×6.52 m(横流向宽度×顺流向长度， 以下同)， 立管2的尺寸为3.1 m×6.2 m， 立管3的尺寸为3 m×6 m， 立管中心距流场入口的距离长度为5D。

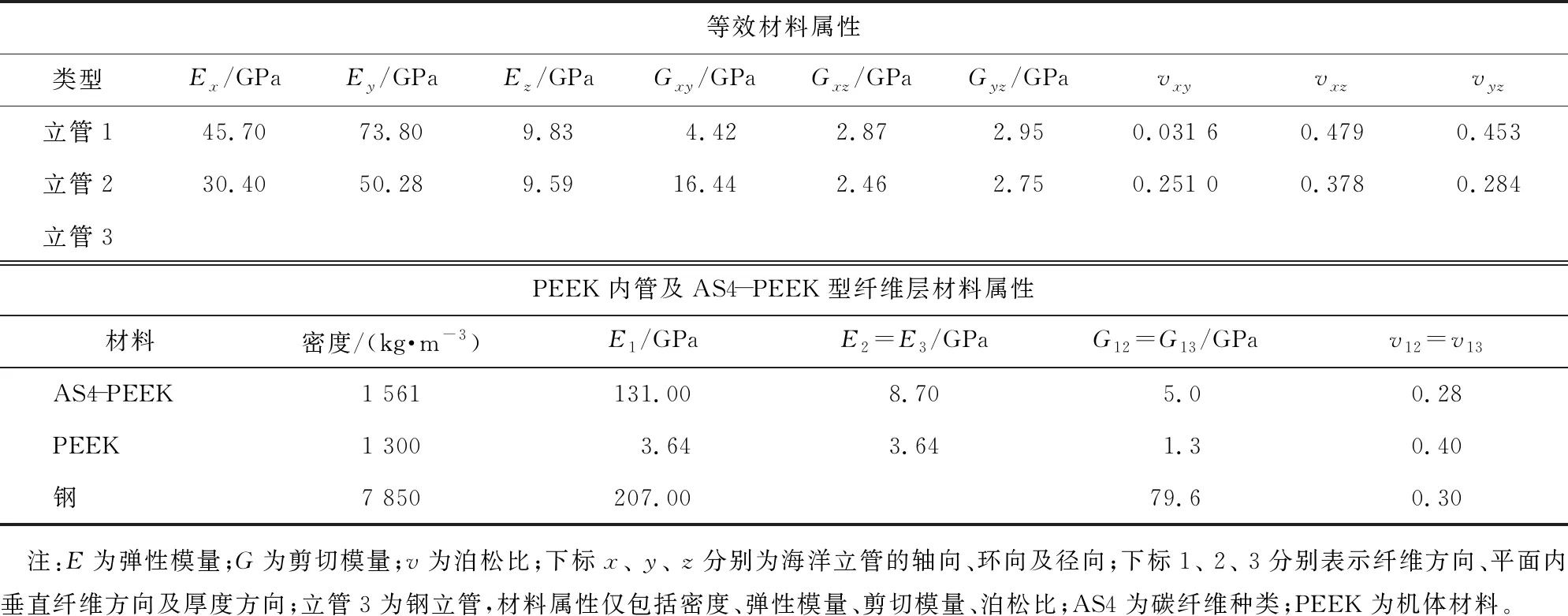
表2 纤维复合材料海洋立管的等效材料属性(等效弹性模量法)及聚醚醚酮(PEEK)内管与AS4-PEEK型纤维层材料属性(层状结构法)

流体场入口、出口、两侧及上、下面分别采用速度边界、流体边界、对称边界及无滑移壁面。使用墨西哥湾海洋立管正常条件下的水文资料作为流场参数，流速U为0.36 m/s，流体密度为1 024 kg/m3，运动黏性系数为1.06×10-6，并采用大涡模拟(LES)进行海洋立管VIV模型的CFD模拟研究。表3所示为3种海洋立管的雷诺数及顶张力。顶张力为海洋立管结构自重的2倍，雷诺数Re为

(9)

为了保证足够的网格精度以模拟漩涡脱落现象，并能反映每个时间步中立管结构变形与流场条件改变之间的相互影响，在立管周围5D×5D区域内进行网格细化并设置动网格。通过ANSYS-ACP、ANSYS-Transient、 Fluent软件实现基于流固耦合作用(FSI)的海洋立管VIV模拟。纤维复合材料数据及结构形式通过ANSYS-ACP、ANSYS-Transient软件交互建立纤维复合材料海洋立管模型，ANSYS-Transient立管计算数据与Fluent软件的流体场计算数据则通过System coupling进行交互，从而综合实现流体场与海洋立管的流固耦合作用。Fluent软件建立的流场在面层设有4 478个单元(包括加密区)，在流场高度方向上划分150个单元，其流体场总单元个数为671 700。纤维复合材料海洋立管采用单元种类为Solid185的单元进行模拟。径向采用240个单元，环向采用20个单元，合计4 800个单元。立管底部采用固接，上部采用铰接，并施加顶张力。三维流场及海洋立管的模型如图1所示。

表3 立管模型雷诺数与顶张力

图1 流场及立管模型图

2 结果分析

2.1 3种海洋立管的频率分析

通过海洋立管VIV模拟，对比等效弹性模量法及层状结构法所得的正交式纤维复合材料海洋立管(立管1)、优化后的纤维复合材料海洋立管(立管2)和金属立管(立管3)的涡激振动特征。由表3可知，3种海洋立管的雷诺数均约为105，即次临界阶段(300≤Re≤3×105)。在此阶段，立管的尾流区域产生周期性交替泄放的紊流漩涡。

根据海洋立管的尺寸、顶张力、浮力、材料属性等进行有预应力模态分析，得到3种海洋立管的自振频率fn及前三阶模态(见表4及图2)。由于3种海洋立管的模态图相同，图2仅以立管2的前三阶模态图为例。在立管的工作环境中，如果其自身固有频率与漩涡脱落频率相近，则会出现频率锁定现象，加剧立管的疲劳破坏。漩涡脱落频率主要受斯特劳哈尔数St、立管直径D以及外流流速U的影响。根据St与Re的关系[15]，确定3种海洋立管的St取值均为0.21。

表4 海洋立管的自振频率、漩涡脱落频率及约化速度

图2 海洋立管2的前三阶模态

对升力系数Cl进行傅里叶变换(FFT)(如图3所示)得到漩涡脱落频率fs，并与

(10)

所得fs相互验证，3种海洋立管的漩涡脱落频率如表4所示。

判断海洋立管的锁振现象时， 也可以采用约化速度

(11)

即当约化速度Ur为4～8[16]时，进入锁振区间。根据表4，由2种海洋立管的约化速度Ur以及漩涡脱落频率fs与其自振频率fn的关系可以看出，在给定条件下，海洋立管不会发生锁振现象。

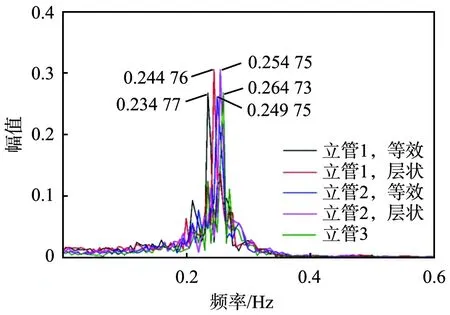
图3 对升力系数Cl进行傅里叶变换所得旋涡脱落频率

2.2 3种海洋立管VIV的CFD模拟结果

采用基于流固耦合作用的CFD三维模型，对3种不同的海洋立管进行数值模拟，选取其3个典型位置(距水面1.2、 6.2、 11.2 m)的位移时程曲线，如图4所示。由图可知，1)在相同海洋环境及立管约束条件下，同种海洋立管：①横流向振动幅值远大于顺流向振动幅值；②横流向振动具有明显的周期性并出现“拍”现象，顺流向振动则趋于稳定在一个较大值附近；③中间部分的位移远大于两端的位移，在靠近固定支撑处最小。2)在相同海洋环境及立管约束条件下，不同种类海洋立管的位移由大到小的顺序为立管2、 立管1、 立管3，与弹性模量的大小顺序正好相反。

(a)-1.2 m处顺流向位移(b)-1.2 m处横流向位移(c)-6.2 m处顺流向位移(d)-6.2 m处横流向位移(e)-11.2 m处顺流向位移(f)-11.2 m处横流向位移图4 3种海洋立管涡激振动时的位移时程

图5所示为3种海洋立管横流向变形。 由图可知， 海洋立管横流向的位移经过初始阶段的增长后， 将保持在一个相对稳定的位置。3种不同立管在相同海洋环境下横流向的最大变形范围相差较大，3种海洋立管横流向变形由大到小的顺序为立管2、立管1、 立管3。

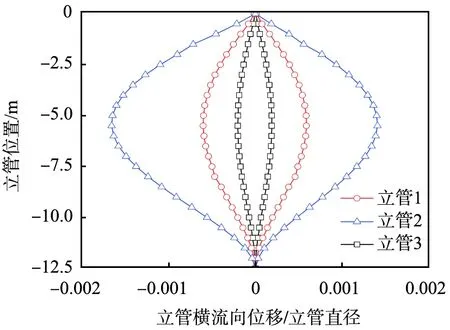
图5 3种海洋立管的最大横流向变形

图6所示为3种海洋立管总位移最大时刻的立管形状。由图可知，3种不同立管在相同海洋环境下顺流向的位移由大到小的顺序为立管2、 立管1、 立管3。

图7、 8所示分别为3种海洋立管最大等效应力及总应力最大时刻的应力分布。从图7、 8中可以看出，等效应力由大到小的顺序为立管3、 立管2、 立管1。此时，立管的应力不再按弹性模量的大小排列，与立管的位移变化情况不同。由此可知，对于应力计算，海洋立管的等效弹性模量不再是最重要的因素。同时，对于金属海洋立管，其等效应力最大处在海洋立管的顶部，这是由其较大自重引起的较大顶张力所导致的；而纤维复合材料海洋立管的应力分布与传统金属海洋立管的应力分布明显不同，其最大应力一般发生在立管的中部或立管的固定端。

图6 3种海洋立管的总位移

图7 3种海洋立管的最大等效应力

采用等效弹性模量法建立纤维复合材料海洋立管时， 可以较好地获得纤维复合材料海立管的整体特性， 但是对于每一层应力分布特征及破坏形式无法分析， 而层状结构法建模方式则可以很好地解决该问题。 图9所示为立管1与立管2利用层状结构法模型所得的各层最大应力， 包括纤维方向应力S1、 垂直纤维方向应力S2与剪切方向应力S12。由图可知，由于结构的构造参数不同，在纤维复合层中，2种立管的应力分布完全不同。立管2纤维增强层中的应力整体上大于立管1纤维增强层中的应力，表明优化后的立管2可以更好地发挥纤维增强层的抗力能力。同时，对比2种立管纤维增强层中的应力分布特征可以发现： 1)对于S1， 立管1的径向纤维层应力较大，而环向纤维层应力较小； 立管2的径向纤维层应力最大， 纤维层增强角度为±52°的纤维层应力的大小居中，而环向纤维层应力最小。 2)对于S2，立管1的环向纤维层应力较大，而径向纤维层应力较小； 立管2的环向纤维层应力最大，纤维层增强角度为±52°的纤维层应力的大小居中，而径向纤维层应力最小。 3)对于S12，立管1由于仅存在正交的纤维增强层， 因此几乎没有剪应力；立管2则会在纤维层增强角度为±52°的纤维层中产生剪应力。

图8 3种海洋立管的应力分布

(a) 立管1

(b)立管2图9 立管1、 2各纤维层的应力分布

3 结论

本文中利用不同的CFD数值模型对3种海洋立管在相同海流速度0.36 m/s时进行VIV模拟，并对3种立管的位移响应特征和应力响应特征进行比较，得出以下主要结论：

1)采用等效弹性模量法及层状结构法分别建立了纤维复合材料海洋立管模型(立管1与立管2)，对于同一纤维复合材料海洋立管，利用2种不同建模方式所得的VIV特征相近。等效弹性模量法建模简单，计算时间短，有利于快速得到立管变形、应力等反映整个立管工作状态的结果；对于层状结构法，虽然建模步骤复杂且计算时间长，但是能直观地显示立管每个纤维层的各项计算结果。由此，需要根据具体的分析要求选择合适的建模方式进行计算。

2)在相同的海洋环境及立管约束条件下，海洋立管的横流向振动幅值远大于顺流向振动幅值。横流向振动具有明显的周期性，而顺流向振动则趋于稳定在一个较大值附近。纤维复合材料海洋立管的最大位移及振幅均远大于传统金属海洋立管的。不同设计方案的纤维复合材料海洋立管的最大位移及振幅也不相同，它们与海洋立管的尺寸、 弹性模量、 顶张力、 支撑条件等有关。

3)由于截面构造及顶张力不同，因此纤维复合材料海洋立管的应力分布与传统金属海洋立管明显不同，其最大应力一般发生在立管中部或立管的固定端，应力包络远小于传统金属海洋立管的。不同设计方案的纤维复合材料海洋立管的应力特征也不相同。