卷积神经网络在锚杆锚固类型识别中的应用

(石家庄铁道大学电气与电子工程学院， 河北石家庄050043)

锚杆广泛应用于桥梁、隧道、建筑等工程。锚杆锚固技术不仅可以合理地调动围岩的自身强度和自稳能力，起到加固和支护围岩的作用，而且成本低，施工方便、安全。该技术在国内和国外发展迅速，但是与此同时，其质量问题很难被发现，一旦出现质量问题将会引起一系列的损失，如人员伤亡和财产损失等[1-3]。另外，由于对锚杆锚固支护原理了解不足，很难掌握锚杆锚固的质量问题，造成大量的成本浪费，因此，需要对锚杆锚固系统进行缺陷检测，以确保支护安全和节约成本。

准确提取锚杆锚固系统特征对类型识别至关重要。传统的特征提取方法依赖于广泛的专业知识和先验知识，不仅要求研究人员理解锚杆锚固系统的结构和原理，而且难以挖掘新特征。神经网络[3-4]和支持向量机[5]等浅层机器学习需要设计专门的特征提取方法来评估锚固质量。例如，小波变换或小波包分解用于提取信号时频域特性，然后将这些特征作为浅层机器学习的输入，但是小波分解或其他特征提取方法不能保证提取到的信号是本质特征。虽然传统的智能识别方法表现良好，但是也存在一些明显的缺点：手动特征提取过程是一个艰苦而耗时的过程，需要研究员大量分析以捕捉代表性的特征；手工特征提取通常取决于现有的特征或评估标准，使得探索新的有用特征变得很困难[6]。为了克服这些缺点，研究一种能够直接从原始信号中学习特征并适应锚杆锚固系统变化的自动特征提取方法具有重要意义。

深度学习[7-9]可以自动从高维数据中学习深层特征，近年来备受各领域研究者的关注。卷积神经网络(CNN)是典型的深度学习方法，其最大的优势是无需过多的预处理，能够直接将原始信号作为网络输入，通过训练调整优化卷积核参数，实现信号的特征提取和分类。CNN模型已成功地应用于许多方面，包括图像识别[10-11]、 故障检测[12-13]和语音识别[14-15]等，然而，很少有研究者使用CNN模型来解决锚固缺陷中的识别问题。

本文中采用一维卷积神经网络(1D-CNN)对锚杆锚固系统类型进行识别，直接以加速度信号作为网络的输入，通过卷积和池化操作来实现端到端的分类过程；同时，对稀疏自编码器一维卷积神经网络 (SAE-1D-CNN)模型与传统的1D-CNN模型、 反向传播(BP)神经网络模型识别方法进行对比。

1 CNN概述

1.1 CNN结构

CNN是受哺乳动物视觉皮层细胞感受野启发而建立的前馈神经网络， 具有局部连接、 权值共享、 降采样等特征， 可以大幅度降低网络的计算成本， 在图像识别和目标检测方面有出色的表现[16]。 图1所示为一个典型的CNN结构， 由输入层、 卷积层、 采样层、 全连接层和输出层组成， 包括特征提取与分类判别2个阶段， 其中， 卷积层、 采样层、 全连接层进行特征提取， 输出层采用SoftMax函数进行分类。

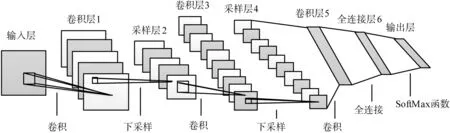
图1 卷积神经网络(CNN)结构图

图1中卷积层包含的多个特征图是通过不同卷积核对上一层的局部区域进行卷积运算得到的。与全局特征提取相比，局部特征提取减少了大量的训练参数，加快了网络的训练。卷积层的另一重要特点是权值共享，进一步减少了卷积层的网络参数，避免了因参数过多而造成的过拟合。卷积层公式为

(1)

采样层又称池化层，该层是对前一层特征图的某个选定区域进行特征分析与统计，用新的特征代表这个区域的整体特征[17]，主要实现以下2个目的:1)减少自由参数的数量，降低网络计算复杂度；2)防止过拟合，使测试集识别率接近训练集识别率。采样方法有平均采样法和最大采样法等。采样公式为

(2)

式中g(· )为采样函数，通常为平均采样或最大采样。

经过几个卷积层和采样层后，连接一个全连接层，该层的每个神经元节点与前一层和后一层的所有神经元节点相连，最后输出层采用SoftMax函数进行分类。

假设标签为k类，输出层公式为

(3)

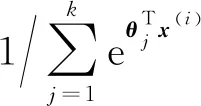
1.2 1D-CNN模型建立

锚杆锚固加速度信号属于一维振动信号，因此，采用一维CNN模型解决锚杆缺陷识别问题。 通过分析锚杆锚固加速度数据特点和实验的实际需要，建立简单的1D-CNN锚杆锚固系统类型识别模型，该模型由输入层、 卷积层1、 采样层1、 卷积层2、 采样层2、 输出层组成，如图2所示。输入层为长度是200的锚杆锚固加速度信号；卷积层1包含5个196×1型特征向量，由5×1型卷积核遍历卷积输入得到；采样层1采用步幅为2的平均池化方法得到5个98×1型特征向量；卷积层2包含10个94×1型特征向量，由5×1型卷积核遍历卷积采样层1得到； 采样层2同样采用步幅为2的平均池化方法得到10个47×1型特征向量；将采样层2的所有特征向量展开成一条向量与输出层全连接进行分类。

区别于传统的锚杆锚固系统类型识别模型，CNN模型包括特征提取与识别2个过程，并且整个网络的参数都通过BP算法进行更新，因此，有较好的稳健性和迁移性。

2 稀疏自编码器

稀疏自编码器(sparse auto-encoder，SAE)是一种无监督的深度学习算法[18]。通过计算自编码的输出与原输入的误差，不断调整自编码器的参数，最终训练出模型。模型的隐含层权重可以看作输入数据的另一种表达方式。

图2 基于一维卷积神经网络的锚杆锚固系统类型识别模型

xi—第i个输入数据，i=1,2,…,5；第i个输出数据，i=1,2,…,5。图3 经典自编码器网络模型

当隐含层维度小于输入层维度时，输入数据可得到一种压缩表示。当隐含层维度大于输入层维度时，向中间层神经元加入稀疏性限制，SAE也可以从数据中提取到有用特征。

SAE损失函数(Loss函数)为

(4)

其中

(5)

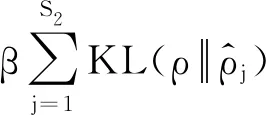
SAE损失函数中的稀疏惩罚项，使用Kullback-Leibler(KL)散度[19]，公式为

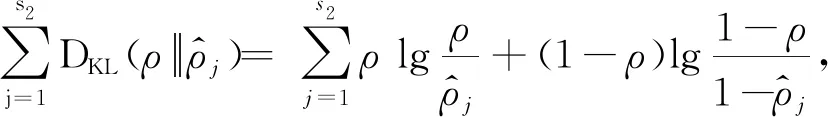
(6)

1D-CNN具有局部连接、 权值共享， 输入数据可为原始信号等优点。 SAE具有快速提取信号基本特征的能力[20]。 将二者结合在一起可以提高1D-CNN卷积层特征提取的速度和准确度。 图4所示为SAE-1D-CNN算法流程。

SAE结构设置是根据本文中建立的1D-CNN锚杆锚固类型识别模型中的卷积层得到的。 由于卷积层1对应5个5×1型的卷积核， 因此， 在锚杆锚固训练数据样本中， 随机选取一部分5×1型的信号段作为SAE模型的输入样本。 隐含层神经元个数设为5， 通过训练SAE模型得到5×5型的隐含层权重作为卷积层1的卷积核初始值。 同理， 利用SAE模型训练采样层1的特征输出得到卷积层2的卷积核初始值。 SAE的训练参数设置如下： 稀疏参数为0.05， 权重衰减因子为0.000 1， 稀疏惩罚项因子为3， 迭代次数为500。

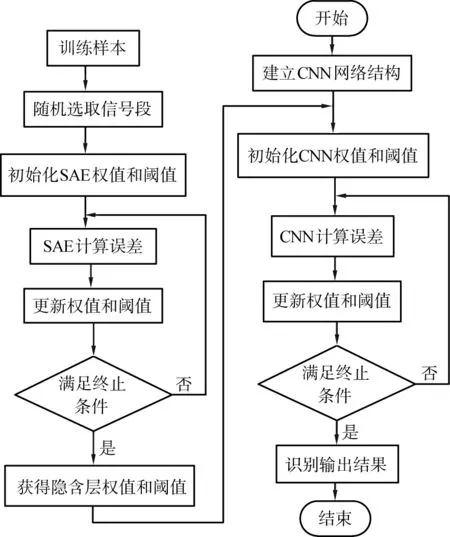
图4 稀疏自编码器(SAE)一维卷积神经网络(CNN)算法流程

3 锚杆锚固系统类型识别结果分析

3.1 锚杆锚固系统实验

为了验证方法的有效性，采用实验的4类锚杆锚固模型进行识别，图5所示为4类锚杆锚固系统模型实物图。图6所示为系统模型切面图，其中1#为完整型锚杆锚固系统模型，2#为缺陷出现在距离锚固界面0.33 m处缺陷长度是0.10 m的锚杆锚固模型，3#为缺陷出现在距离锚固界面0.70 m处缺陷长度是0.10 m的锚杆锚固模型，4#为缺陷分别出现在距离锚固界面0.52、1.08 m处缺陷长度分别为0.11、 0.12 m的锚杆锚固模型。模型参数见表1。

实验中，将压电集成电路(IEPE)加速度传感器放置于锚杆的端部， 另一端接到动态信号测试分析装置的一个通道上，测试分析系统与计算机相连。所有设备连接好后，检查小锤、 传感器、 信号采集装置之间的连线是否牢固，然后设置系统软件参数，其中采集频率设为10 kHz。最后，点击信号处理界面的采集按钮即可完成信号采集。为了避免外界因素对实验数据采集造成干扰，在信号采集过程中，需要注意小锤敲击的准确性，每次敲击力度尽量保持一致。图7所示为锚杆加速度信号采集系统设备的连接示意图，图8所示为得到的锚杆锚固加速度信号。

图5 4类锚杆锚固模型

(a)1#(b)2#(c)3#(d)4#图6 4类锚杆锚固模型切面

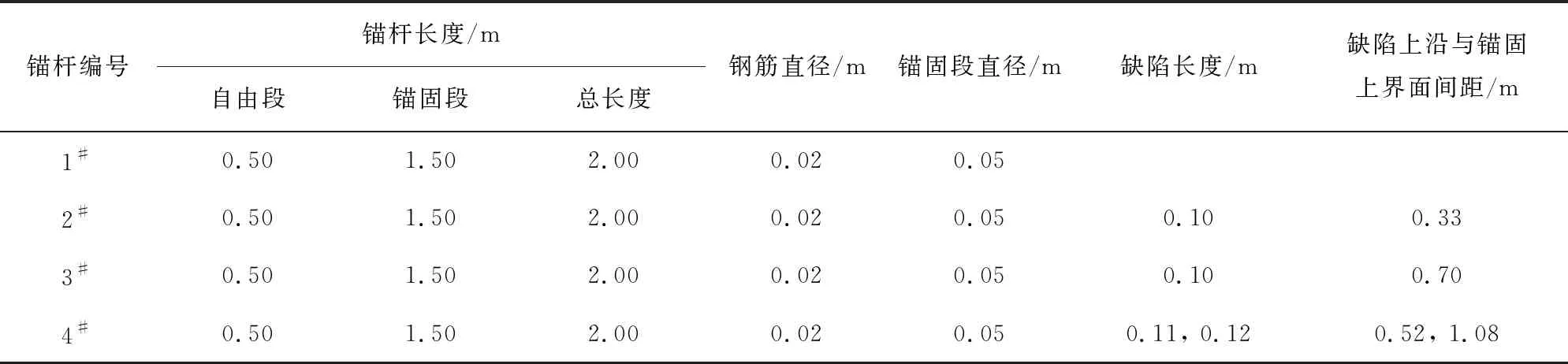
表1 锚杆锚固系统模型参数

图7 系统设备连接示意图

3.2 识别结果分析

利用实验室搭建的锚杆锚固实验平台得到4类锚杆锚固数据各260组， 共1 040组。 其中每组数据包含1 024个采样点， 如果将每组数据的采样点都作为1D-CNN的输入， 不仅会延长训练时间， 而且容易造成特征冗余， 进而导致锚杆锚固类型的识别效果不理想。 从图8中可以看出，处于0.02 ～0.04 s的信号波形变化较明显， 该段信号包含4类锚杆锚固系统的不同特征， 因此， 只需要将这段时间的采样点进行识别， 即每个样本包含200个数据点。为了检验CNN模型的泛化能力， 将1 040组数据进行随机排序， 并从中选取900组作为训练集和140组作为测试集本。 网络训练参数设置学习率为1， 批处理长度为30， 迭代次数为300。分别采用SAE-1D-CNN模型、 传统1D-CNN模型和BP神经网络模型对锚杆锚固加速度数据进行识别测试。 其中， SAE-1D-CNN模型中SAE的损失值曲线如图9所示。 从图中可知， 当迭代次数达到400时， 损失函数开始收敛， 最终损失函数值稳定在0.353左右。

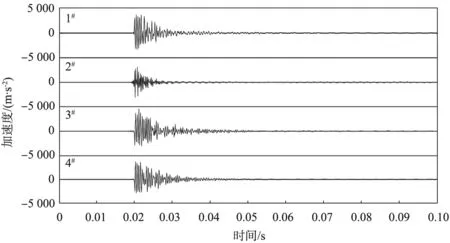
图8 锚杆锚固加速度曲线

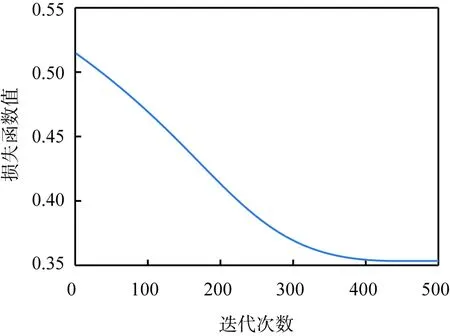
图9 稀疏自编码器的损失值曲线

图10所示为3种模型识别结果。从图中可以看出，1D-CNN模型的正确识别样本数为134，错误识别样本个数为6，识别准确率为95.71%。SAE-1D-CNN模型的正确识别样本个数为138，错误识别样本个数为2，识别准确率为98.57%。BP模型的正确识别样本个数为100，错误识别样本个数为40，识别准确率为71.43%。结果表明，SAE-1D-CNN、传统1D-CNN模型在实验中的识别正确率均高于BP模型的，说明CNN模型独特的体系结构可以自动分层的挖掘数据更具代表性的信息。与传统1D-CNN模型在锚杆锚固系统识别任务中相比，SAE-1D-CNN模型表现出了更好的识别效果。

图11所示为2种锚杆锚固类型识别模型的训练集均方误差曲线。由图可知，SAE-1D-CNN模型收敛更快，均方误差更小。随着网络迭代次数的增加，2种模型的训练集均方误差均减小，但是减小程度不同，前2 000次批量迭代中SAE-1D-CNN模型的均方误差减小远快于1D-CNN模型的，其原因是SAE-1D-CNN模型的卷积核进行了预训练，有效地提取了信号的基本特征，进而增大了CNN卷积层特征提取的速度和改善了准确度； 但是， 由于1D-CNN模型的卷积核未进行预训练，因此，需要更多次批量迭代训练来提取特征以减小训练集的均方误差。

(a)一维卷积神经网络模型

(b)稀疏自编码器一维卷积神经网络模型

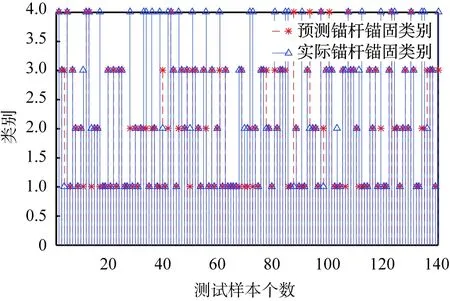
(c)反向传播模型图10 不同模型的锚杆锚固类型识别结果

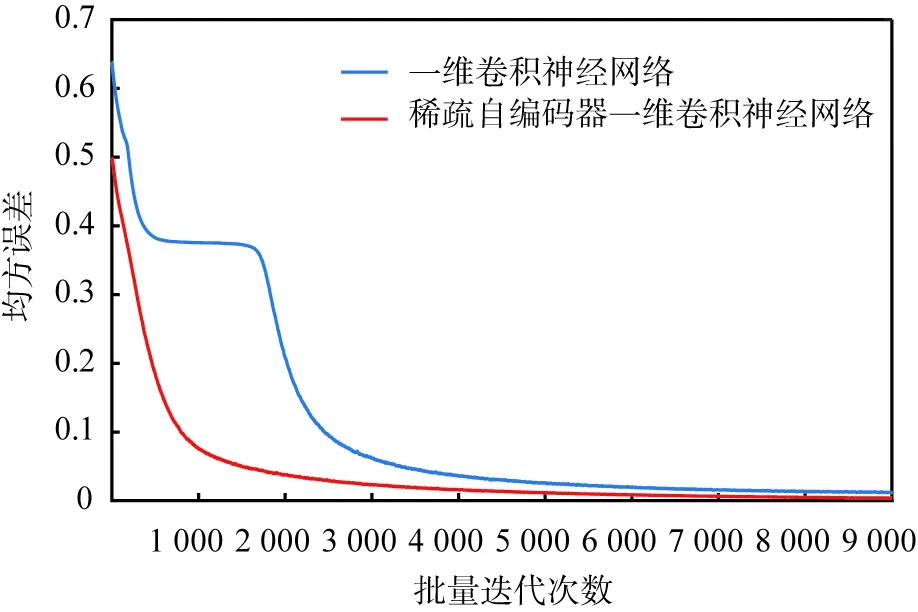
图11 训练集均方误差曲线

4 结语

本文中采用1D-CNN模型对锚杆锚固系统类型进行识别，模型直接从锚杆锚固加速度信号中自动学习特征，完成端到端的类型识别，并且为了避免网络在训练时收敛慢、 易陷入局部最优值，利用SAE算法对卷积核进行预训练。通过分析和比较识别结果，SAE-1D-CNN模型不仅提高了锚杆锚固系统类型的识别率，而且与传统1D-CNN模型和BP神经网络模型相比，收敛更快，均方误差更小。

由于实验条件有限，锚杆锚固模型的缺陷种类较少，尤其是很多工程中的锚杆锚固缺陷类型未涉及到，因此，在今后的研究工作中，可以通过加入更多的锚杆锚固缺陷种类，使CNN模型在锚杆锚固缺陷类型识别中具有更大的实用性。