基于K-奇异值分解字典学习的振动信号压缩感知方法
何天远, 王万仁2, 吴鲁明, 邢亚航, 郝如江
(1. 石家庄铁道大学机械工程学院, 河北石家庄050043; 2. 中铁二十二局集团轨道工程有限公司, 北京100040)
齿轮箱的状态监测和故障诊断对预防突发事故和维持机械设备正常运行具有重大的意义。在齿轮箱故障诊断研究中,很少有对信号采集方面的研究。目前被广泛采用的振动信号采样方法是以采样频率必须大于信号中最高频率2倍的奈奎斯特采样定理为基础的。近年来,随着大型机械设备向综合、高速、连续和网络化趋势发展,如果依然用基于奈奎斯特采样定理的采集系统采集信号,就会产生较高的采样频率,同时会产生海量的监测数据[1],因此,齿轮箱状态监测得到的海量数据面临着难以实时传输和储存过慢的问题。近几年出现的压缩感知(compressed sensing, CS)采样突破了传统的奈奎斯特采样定理[2]的限制。CS理论通过以远低于奈奎斯特采样速率的频率对信号进行压缩采样并且直接得到信号的压缩表示,不需要经过信号采样和压缩2个单独的过程,就达到采样和压缩同时进行的目的。最后,利用适当的CS重构算法就可以高概率地重构出原始信号[3]。
针对上述问题,本文中提出基于K-奇异值分解(K-singular value decomposition, K-SVD)字典学习的振动信号CS方法,用以提高重构信号与原始信号的相似度,并且最大程度地保留原始信号的频率特征。实验分别以基于K-SVD训练生成的2种字典和离散余弦变换(discrete cosine transform, DCT)固定字典为稀疏矩阵,用L1范数重构算法对原始信号进行重构,并对实验结果进行对比分析。
1 CS理论
CS利用数据的冗余特性,只采集少量有用的样本来还原真实的采集数据[4]。在采集数据时直接采集q个有效的测量值,而不是满足传统的奈奎斯特采样定律的要求,即采样频率必须是信号最高频率的2倍或以上。CS以采集的原始信号在变换域上稀疏作为前提条件,用测量矩阵观测被测信号,再由观测值结合重构算法,如L1范数算法、正交匹配追踪(orthogonal matching pursuit, OMP)算法等来重构原始信号[5]。
CS理论的公式为
y=Φf
,
(1)
式中:y为观测矢量且y∈m×1,m为观测矢量的维度;Φ为测量矩阵;f为原始信号且f∈n×1,n为原始信号的维度。f可表示为
f=φα
,
(2)
式中:φ为正交基矩阵;α为稀疏矢量。
CS理论公式中的测量矩阵Φ需要满足一定的不相关性,即与φ不相关。由式(1)、(2)联立可得表达式
y=Φφα
。
(3)
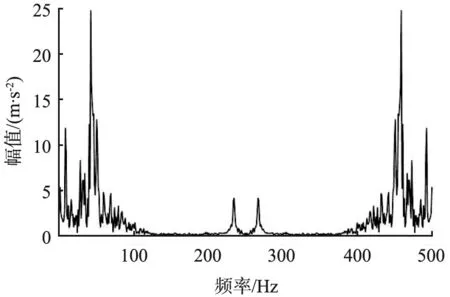
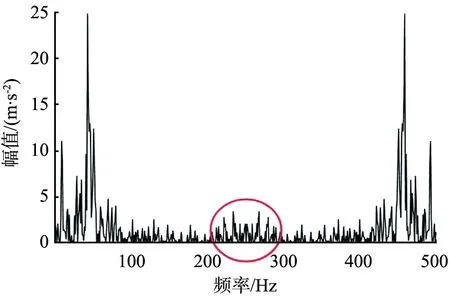
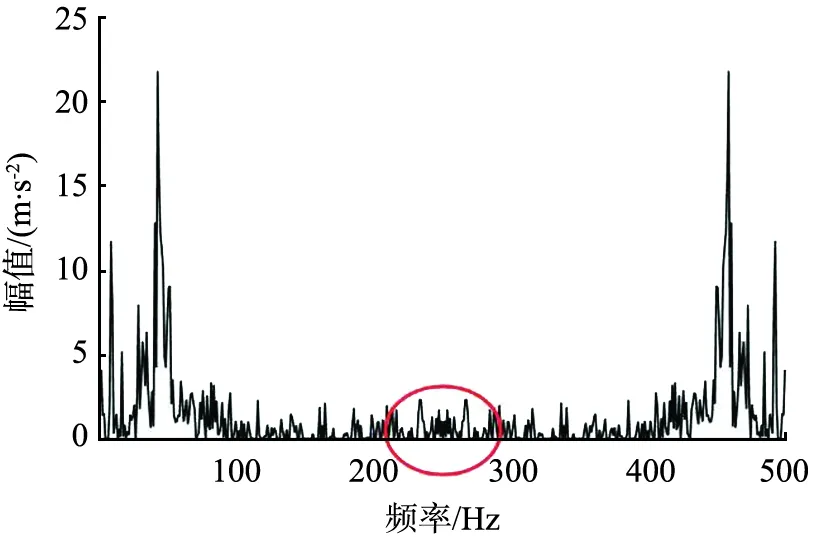
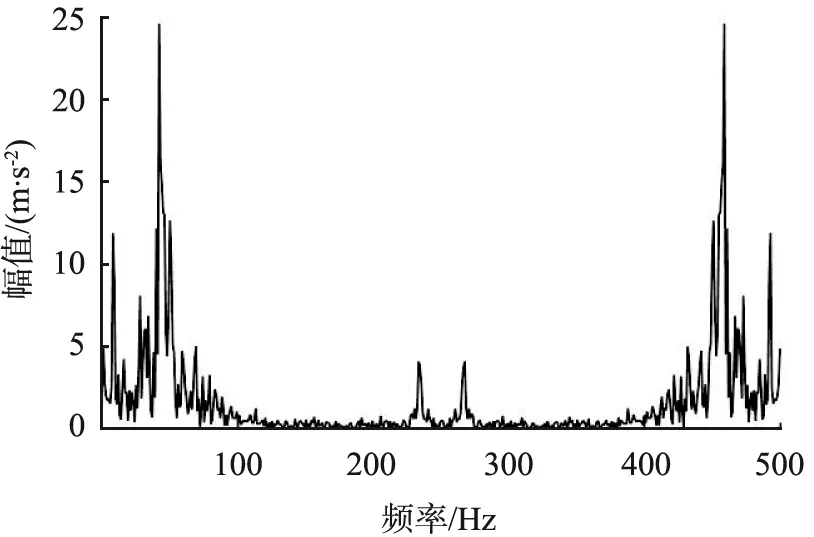
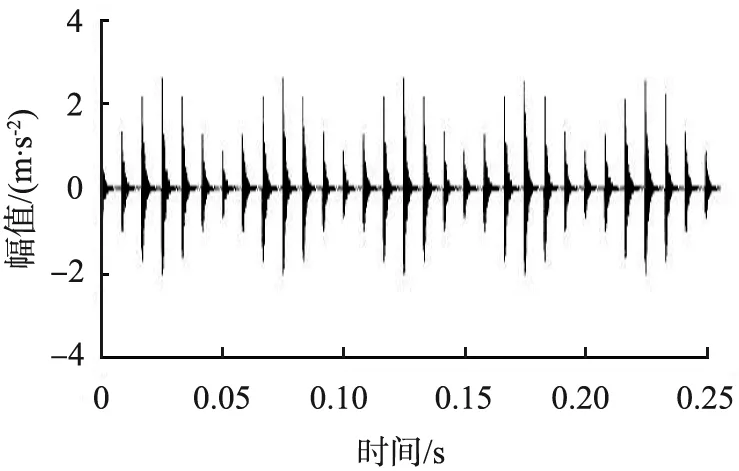
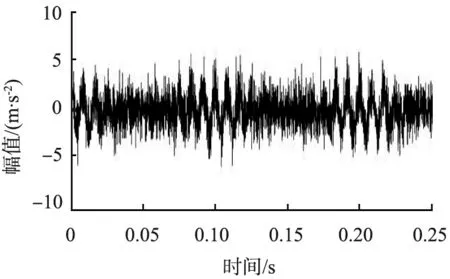
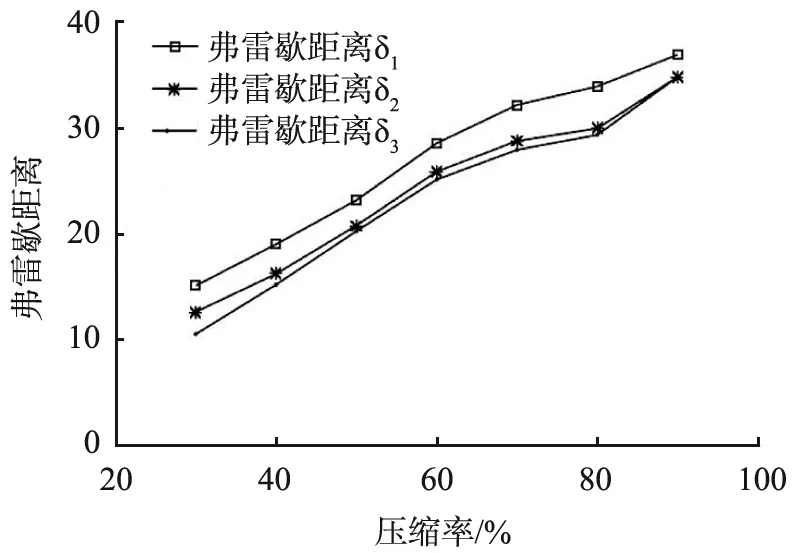
稀疏矢量是r稀疏的,且r (4) 求解式(4)常用的有L1范数算法、基追踪算法和OMP算法等。CS有2个重要的条件,即稀疏性和约束等距性(restricted isometry property, RIP)[6]。原始信号f是稀疏的,或者在某个变换域内是稀疏的。测量矩阵Φ则需要满足RIP条件, (5) 式中A为感知矩阵。当Φ为高斯随机矩阵时,虽然完备字典为非正交基,但感知矩阵也具有随机性,仍可满足CS的RIP性质。 Aharon等[7]提出了一种K-SVD的字典训练方法。K-SVD类似于K均值算法的一种泛化形式,其核心思想是通过稀疏约束问题的追踪和奇异值分解算法的交替进行,实现字典与稀疏系数的更新。K-SVD算法需要构造稀疏字典对数据进行稀疏表示,在语音信号压缩、图像压缩、体征信号处理等方面已被广泛应用。 稀疏表示的理论公式为 Y=dX , (6) 式中:Y为样本矩阵且Y∈w×N,w为字典中每个样本的维度,N为样本数;d为过完备字典且d∈w×k(k>w),k为一个系数的长度或训练字典中的原子数;X为系数矩阵且X∈k×N。 式(6)的目的是找到让系数矩阵X尽量稀疏的字典d,寻找最优解(X最稀疏)是非确定性多项式难题(non-deterministic polynomial hard, NP-Hard),只能逐步逼近最优解。 创建一个初始字典,可以是DCT固定字典、小波字典,也可以由采集到的振动信号生成。用该字典对采集的振动信号稀疏表示,即让数据表达尽可能全面,系数尽可能小,并得到稀疏表示的系数矩阵X。将dX分解,也就是用d中的行乘与之对应X中的列,即 (7) 式中:di为过完备字典d的行;xi为系数矩阵X的列。最后将dixi逐个优化。 直接把初始字典作为过完备字典会使具有稀疏性的系数矩阵所表示的数据与原始数据相比误差较大。减小误差的方法是在满足稀疏度的条件下逐行逐列更新优化,逼近可用字典。计算当前误差矩阵的表达式为 (8) 产生的误差为 , (9) 在分离第k个基分量之后会产生一个空位,而SVD的作用就是找到更适合的基分量来填充这个空位。当误差稳定时,更新的字典基本收敛。 K-SVD的求解是一个迭代过程。首先,假设字典d是固定的,用OMP、基追踪、L1范数等算法,都可以得到使Y稀疏表示的系数矩阵X,然后固定X,根据X来更新字典d,如此循环直到收敛为止[8]。 在求解过程中过完备字典d需要逐列更新。首先,假设系数矩阵X和过完备字典d是固定的,当过完备字典中的第k列dk更新时,dk对应系数矩阵X中第k行为xk,则 (10) 为了验证基于K-SVD字典学习的振动信号CS方法是可以提高信号重构性能的,设置如下仿真信号进行分析。此仿真信号模拟的是轴承内圈局部故障时的振动信号。信号的采样频率为16 000 Hz,采样点数为4 000。 U(t-hT-τh)2[1-0.5cos(2πfrt)] +n(t), (11) 式中:t为时间节点;冲击次数h=1, 2, … ;fr为转频,值为20 Hz;fn为共振频率,值为5 000 Hz;C为信号衰减系数, 值为1 000;τh是第h次冲击相对于特征周期T的微小波动, 随机波动服从均值为0的正态分布; 标准差为转频的0.5%;n(t)为高斯噪声, 标准差为2, 加入噪声后的信号信噪比为-11.27 dB;U(t)为单位阶跃函数。 计算所得故障特征频率fu=3.906 Hz[9]。 冲击信号波形图和仿真信号波形图如图1所示。从图中可以明显看出,噪声完全掩盖了周期冲击成分,没有规律可循。 (a)冲击信号 (b)仿真信号图1 冲击信号与仿真信号波形图 实验分为3组,在采集的振动信号中随机选取500个点作为CS测量数据x1,以3组不同的特定字典为基字典,最后用L1范数算法重构信号。 3组特定的字典分别如下: 1)以DCT固定字典为基字典d1; 2)以一部分采集的振动信号为训练样本,DCT固定字典为初始字典,利用K-SVD模型生成特定基字典d2; 3)以一部分采集的振动信号为训练样本,用训练样本生成矩阵作为初始字典,利用K-SVD模型生成特定基字典d3。 当压缩率为60%时, 仿真信号频域图如图2(a)所示; 以d1、d2、d3为基字典的重构信号频域图如图2(b)、 (c)、 (d)所示。 对比图可看出, 经过K-SVD训练过的字典在振动信号压缩采样中的效果更好,而且图2(b)中突出频率被淹没在毛刺中,突出频率十分不明显。 (a)仿真信号频域图 (b)基字典为d1,重构频域图 (c)基字典为d2,重构频域图 (d)基字典为d3,重构频域图图2 仿真信号频域图与基字典为d1、 d2、 d3时的重构频域图 本文中采用弗雷歇距离δ来评价重构信号与原信号的相似度,采用压缩率来衡量振动信号的压缩程度。 弗雷歇距离是1906年法国数学家Maurice René Fréchet提出的一种基于空间路径相似度的描述方式,其着重将路径空间距离考虑进去,对于有一定空间时序的曲线相似度的评价效率更高[10]。 弗雷歇距离就是使最大距离在最小化采样方式下的比值。弗雷歇距离越小,说明重构信号与原始信号的差异越小,2条曲线相似度越高。其数学表达式为 (12) 式中:j为原信号轨迹PF的长度;u为重构信号轨迹QF的长度;α(b)为原信号运动位置描述函数;β(b)为重构信号运动位置描述函数; 若将变量b约束到区间[0, 1]内, 则有α(0)=0,α(1)=j,β(0)=0,β(1)=u。 在压缩率分别为30%、40%、50%、60%、70%、80%、90%时,计算原始信号与字典d1产生的重构信号的弗雷歇距离δ1、 原始信号与字典d2产生的重构信号的弗雷歇距离δ2、 原始信号与字典d3产生的重构信号的弗雷歇距离δ3。 仿真实验结果如图3所示。从图中可以很明显地观察出,在压缩率相同时,经过K-SVD训练过的字典能更好地还原信号,而且以训练样本为初始字典,经过K-SVD模型训练生成的特定字典d3的效果最好。 图3 仿真信号在不同压缩率时的弗雷歇距离 采用图4所示的动力传动故障诊断综合实验台,采集振动信号并对其进行实验验证。实验中电机的转频为40 Hz,采样频率为12.5 kHz。 图4 动力传动故障诊断综合实验台 实验同样分为3组,在采集的振动信号中随机选取500个点作为CS测量数据x2,以3组不同的特定字典为基字典,最后用L1范数算法重构信号。 3组特定的字典分别如下: 1)以DCT固定字典为基字典d4; 2)以一部分采集的振动信号为训练样本,DCT固定字典为初始字典,利用K-SVD模型生成特定字典d5; 3)以一部分采集的振动信号为训练样本,用训练样本生成的矩阵作为初始字典,利用K-SVD模型生成特定字典d6。 压缩率为60%时,实测信号频域图如图5(a)所示;以d4、d5、d6为基字典的重构信号频域图如图5(b)、 (c)、 (d)所示。对比图5可知特定字典d6在振动信号压缩采样中的效果更好,而且图5(b)、 (c)中的部分突出频率被淹没在毛刺中,突出频率极不明显。 实验结果如图6所示。 从图中可以明显地观察出,在压缩率相同时经过K-SVD训练过的字典能更好地还原信号,且此方法对于实测信号适用。 为了对振动信号更好地进行压缩传输,本文中提出了一种基于K-SVD字典学习的振动信号CS方法。实验中分别利用3 种不同的字典作为基字典对信号进行重构,实验结果表明,经过K-SVD训练过的字典能有效地提高重构精度。 (a)实测信号频域图 (b)基字典为d4,重构频域图 (c)基字典为d5,重构频域图 (d)基字典为d6,重构频域图图5 实测信号频域图与基字典为d4、 d5、 d6时的重构频域图 图6 实测信号在不同压缩率时的弗雷歇距离2 K-SVD方法
2.1 稀疏表示
2.2 字典更新
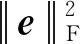
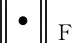
2.3 求解流程
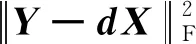

3 仿真分析
3.1 仿真信号
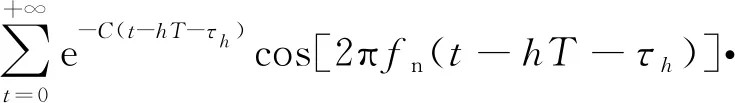
3.2 仿真结果对比分析




4 实验分析
4.1 实验介绍

4.2 实验结果对比分析
5 结语