NOD误差下非参数回归模型中小波估计的强相合性

邓新，桂代运，许志才

(滁州学院数学与金融学院，安徽 滁州 239000)

0 引言

考虑如下带有重复测量的非参数回归模型：

Y(j)(xni)=g(xni)+e(j)(xni)，j=1,2,…,m

(1)

其中g(·)是定义在[0,1]上的未知回归函数，Y(j)(xni)是在xni处的第j次观测值，0≤xn1≤…≤xnn≤1，e(j)(xni)是均值为0的随机误差，m为试验次数.

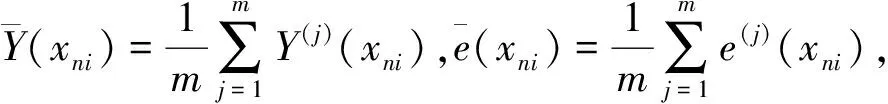
沿用文献[1]中方法，定义g(·)的小波估计：

(2)

其中Ai=[si-1,si]是区间[0,1]上的一个划分，xni∈Ai，1≤i≤n，并且k=k(n)>0是仅依赖于n的整数. 小波核Ek(x,s)定义如下：

其中Z是整数集，φ(·)是尺度函数.

在很多统计问题中，一般假定随机误差是独立的，但在实际应用中是不合理的，本文中主要讨论较为广泛的相依误差结构——NOD(negatively orthant dependent)随机误差，在这种误差下，研究非参数模型(1)中未知函数g(·)的小波估计(2)的强相合性. 下面给出NOD序列的概念.

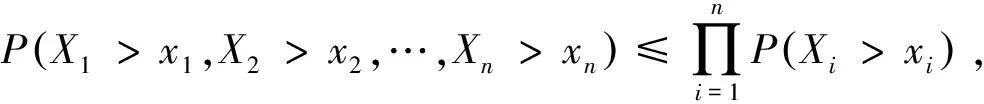
NOD序列是一类包含独立和NA(negatively associated)序列在内的、更弱的负相依序列，其研究成果也相当丰富. 比如，Volodin[2]建立了Kolmogorov不等式，Asadian等[3]得到了Rosenthal型不等式，Chen等[4]及Wu等[5]研究了完全收敛性及完全矩收敛性，Wang等[6]讨论了非参数回归模型中估计量的完全相合性，等等. 本研究将利用NOD序列的Rosenthal型矩不等式和Kolmogorov强大数定律，建立NOD误差下模型(1)中小波估计的强相合性，所得结果推广了Zhou等[7]中关于NA误差的相应结果.

接下来，给出本文中用到的随机控制的定义.

定义2称随机变量序列{Xn,n≥1}是被随机变量X随机控制的，如果存在正常数C，使得对任意的n≥1和∀x≥0，有P(|Xn|>x)≤CP(|X|>x).

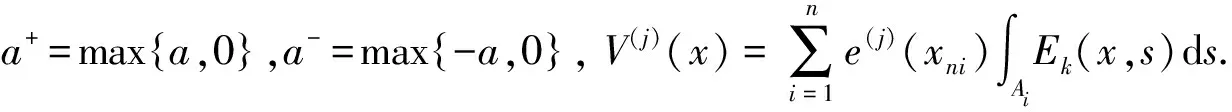
1 假设条件及主要引理

首先给出如下假设条件.

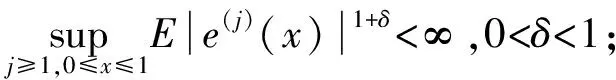
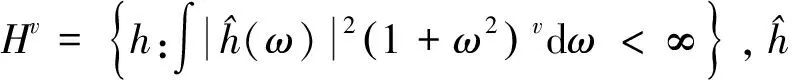
A3)g(·)满足γ>0阶Lipschitz条件；

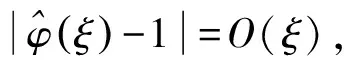
为证明主要结果，需要下面的重要引理.

引理1[9]设随机变量X1,X2,…,Xn是NOD的，f1,f2,…,fn都是非降(或非增)函数，则随机变量f1(X1),f2(X2),…,fn(Xn)是NOD的.

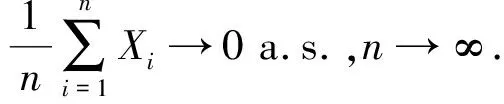
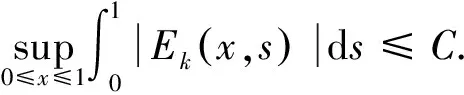
引理5[1]若假设A4)、A5)成立，h(x)满足A2)、A3)，则

2 主要结果及其证明

定理1的证明首先，借助于凸函数性质及引理4，容易验证

(3)

然后，注意到

(4)

(5)

类似可得

(6)

最后，所证结果由(3)、(4)式得到.

定理2的证明注意到

(7)

取0<θ<1，对于1≤j≤m，令

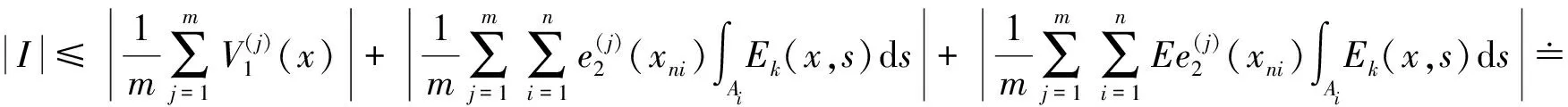
从而，由Borel-Cantelli引理，立得I1→0 a.s.，m→∞.

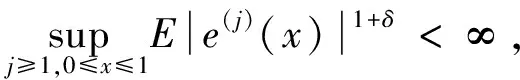
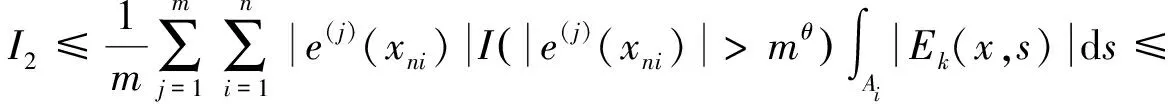
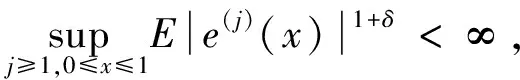
由此，(7)式成立，该定理得证.

注2定理2中结果也同样适用于独立和NA随机误差情形.