相关变步长自适应算法在TDLAS系统中的应用

吴 臣，武 斌，陈 志，张永明

(1.天津城建大学计算机与信息工程学院，天津 300384；2.天津大学，精密测试技术及仪器国家重点实验室，天津 300072)

0 引言

可调谐二极管激光吸收光谱(TDLAS)技术为基于朗伯-比尔定律(lambert-beer law)的红外吸收光谱检测技术的一种，在痕量气体检测中通常采用波长调制光谱(WMS)技术加入正弦调制信号，其中以锁相放大器解调二次谐波信号从而反演气体浓度最为常用[1-2]。测量系统中应用电路所产生的噪声、光强调制中伴随的剩余幅度调制(RAM)等噪声会导致检测结果信噪比低，使系统难以实现痕量气体的高精度检测[3]。目前，在TDLAS技术中常用的数字滤波方法有：Gabor变换[4]、加权滑动平均滤波算法[5]、奇异值分解矩阵分析方法[6]等，虽然提升了一定的信噪比，但对噪声变化的适应性较差，因此采取自适应滤波算法以提升系统信噪比。

基于最小均方误差(LMS)的自适应滤波算法能够根据噪声变化自适应调整滤波器权值系数以达到最优滤波效果，而定步长LSM算法存在收敛速度与稳态精度方面的矛盾，为解决此矛盾，覃景繁等提出的基于Sigmoid函数的SVSLMS自适应滤波算法[7]，路翠华等提出的基于箕舌线的变步长自适应算法[8]，卢炳乾等提出的基于正弦函数的新变步长LMS算法[9]，上述算法构建了步长因子与误差信号功率的函数关系，而在TDLAS系统噪声消除应用中，算法收敛阶段误差信号是对不含噪声的原始信号的最佳估计，所以原始信号的增大会使步长增大，影响算法的稳态精度。文献[10]所述MVSSLMS利用误差信号前后时刻的自相关时间均值作为自变量对步长进行调节[10]，但在算法收敛阶段其自相关均值较小，从而容易导致步长在算法未收敛前达到最小值，导致算法早熟。

为了更好地在TDLAS检测系统中应用自适应滤波算法，本文提出的C-VSSLMS采用了新的步长更新函数并以输入信号与误差信号的相关系数调整步长因子，减弱了原始信号变化对步长的影响，应用仿真测试使用Simulink仿真平台构建TDLAS系统模型，并在信号处理部分嵌入基于改进算法的自适应滤波器，实验结果表明改进算法在保证稳态精度的同时具备了更快的收敛速度，并且对系统噪声具备良好的抑制作用，达到了预期的效果。

1 TDLAS系统噪声来源

在基于TDLAS技术的气体检测系统中，噪声主要包括两大部分，其一为残余幅度调制(RAM)引起的基线漂移噪声，其二为探测器噪声等随机噪声。

激光器输出波长在待测气体可吸收峰附近小范围扫描的同时，以波长调制技术对激光的波长进行高频正弦调制，与此同时，激光器的输出光强也会被调制，激光器光强调制分为线性调制和非线性调制，其中非线性部分会带来剩余幅度调制(RAM)噪声，RAM在二次谐波的检测中会引入奇次谐波分量，导致二次谐波信号的线型畸变等问题，对气体浓度反演造成影响[11-13]，输出光强I(t)可表示为

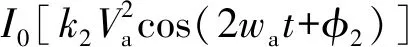
(1)

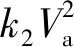
因此系统中光电探测器输出信号：

Iout(t)=I1(t)+I2(t)+N(t)

(2)

式中：I1(t)为激光器输出光强调制线性部分经光电探测器输出的原始信号；I2(t)为激光光强调制的非线性部分，其会引起与被测特征无关的RAM噪声；噪声N(t)主要包括散粒噪声、热噪声等，这部分噪声具备白噪声的频谱特性。

2 基于相关系数的变步长自适应滤波

2.1 自适应滤波原理

基于LMS自适应滤波算法原理框图如图1所示，信号源包括原始信号s(i)以及噪声n(i)，其作为自适应滤波器的期望信号d(i)输入，针对期望信号中噪声分量的估计信号作为自适应滤波器的输入信号x(i)，滤波器输出信号为y(i)，系统输出的误差信号为e(i)。其基本原理为经基于最小均方误差算法的迭代公式对数字滤波器的权系数W(i)进行自适应调节使滤波的输出信号对期望信号中的噪声分量进行逼近，当e(i)取最小值时即为原始信号s(i)的最佳估计。

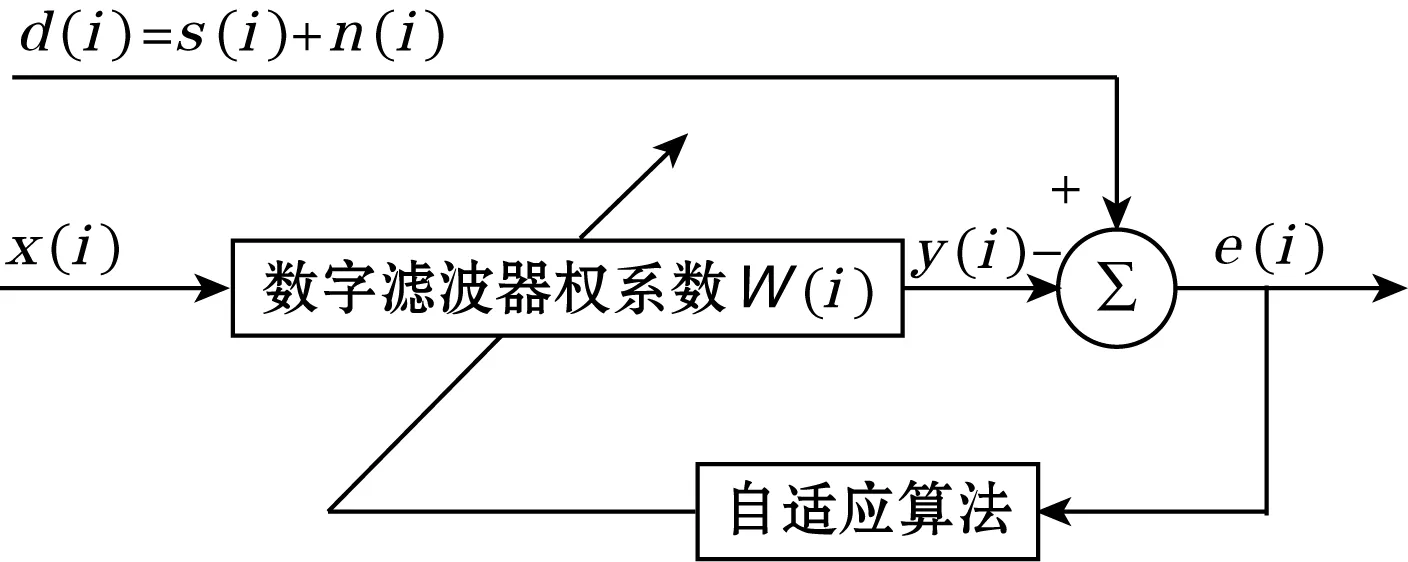
图1 自适应噪声抵消原理框图

基于最小均方误差的自适应滤波算法中常用的迭代公式为

(3)

由式(3)可知，步长因子μ为固定值，从而选取较小的步长因子会导致算法前期收敛速度慢，迭代周期过长；而选取较大的步长因子虽然会使算法收敛速度快，但算法后期相对较大的步长因子导致算法稳态误差增大[13]，变步长算法的核心思想为算法初始阶段有较大步长以加快收敛，在趋于收敛阶段步长缓慢下降以具备较好的稳态误差[14]，故采用变步长自适应滤波算法。

2.2 改进的变步长自适应滤波算法

通过对TDLAS系统噪声的分析可知在时域上存在原始信号与噪声互不相关的特点，故变步长自适应滤波算法以输入信号x(i)与误差信号e(i)的相关性大小作为步长因子更新的自变量，并且在步长因子μ(i)更新的非线性函数模型选择上以sinc函数为基本原型，通过对sinc函数的翻转平移变换以满足变步长的调整原则，而为了克服所选步长调整函数自变量定义域范围过大导致步长过大从而使算法难以收敛的缺点，采用输入信号与误差信号的相关系数R[x(i),e(i)]作为自变量，其取值范围为(0,1)，从而削弱了定义域范围过大对步长因子取值的影响，由此可得步长μ(i)与R[x(i),e(i)]的表达式为

(5)

式中：β控制步长取值；α控制函数线型。

改变α、β2个参数对函数模型的影响如图2所示。

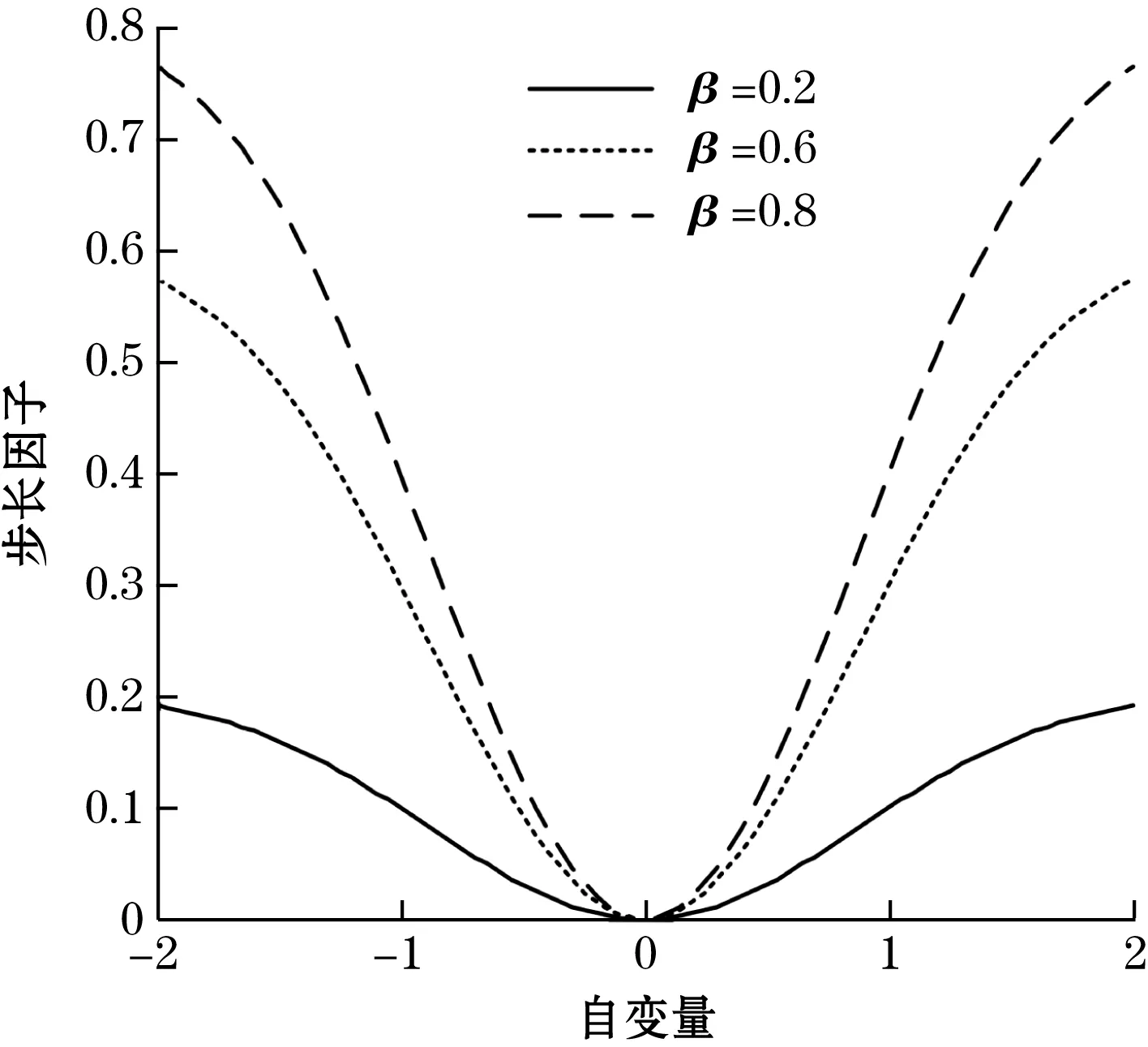
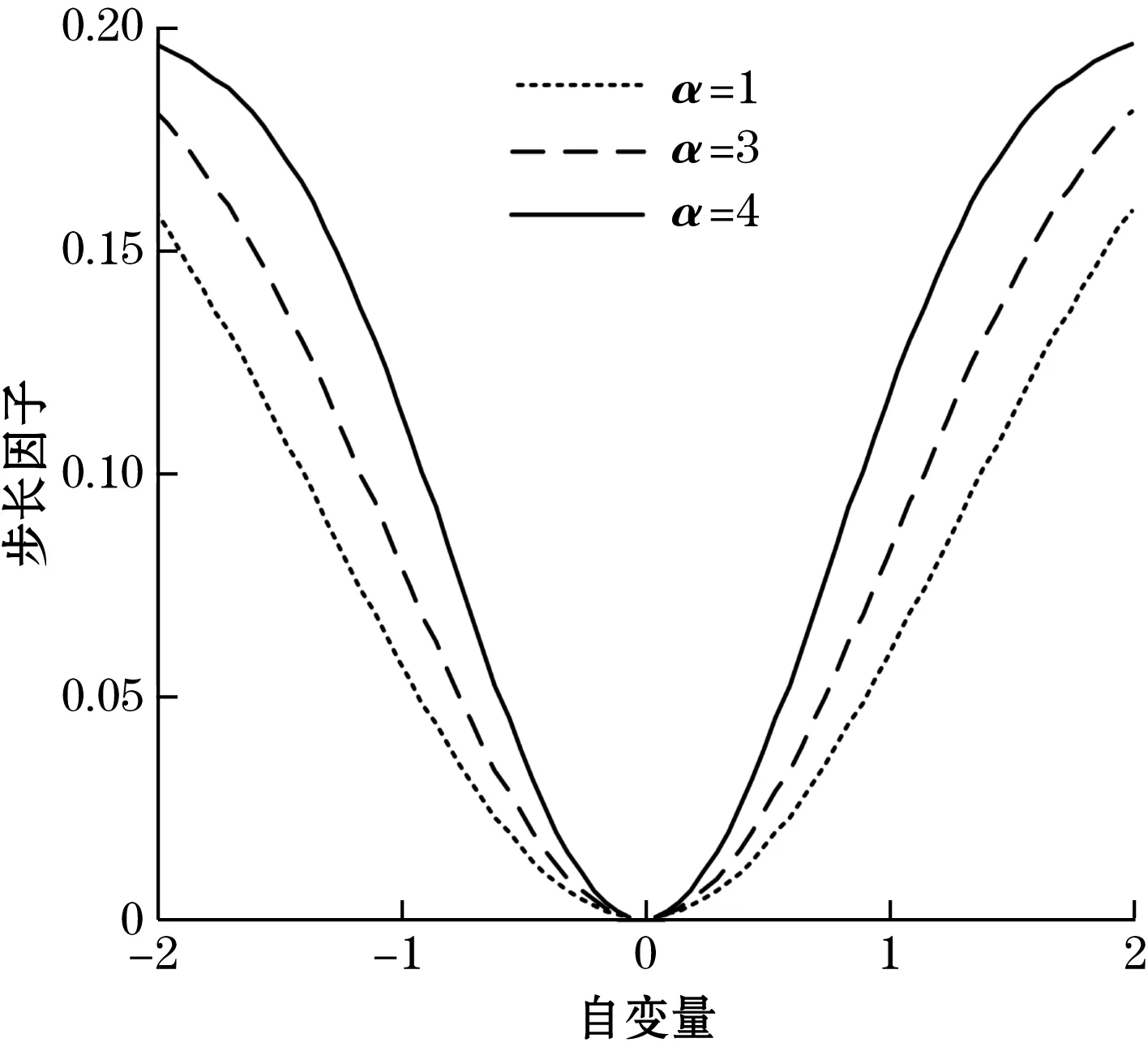
图2 参数β，α变化对函数模型的影响

由图2可知，参数β控制步长的取值，步长μ与β成类正比关系，为了保证收敛阶段算法具备较小的稳态误差，初始步长不宜过大，参数β选值应尽量小于1；参数α控制函数线型，由图2可知，α值较大时算法前期步长不会过快衰减且线型越接近理想变化，但α的增大伴随着算法复杂度的增加，使系统响应时间变长，因此综合分析，对于参数α的取值应酌情选取在3～5，该参数范围可以在保证算法稳定性的前提下使算法前期具备较快的收敛速度。

根据对TDLAS系统噪声分析中所述，噪声与原始信号存在时域不相关的特性，因此本文采取以相关系数R[x(i),e(i)]作为步长因子更新函数的自变量，即：

(6)

由式(6)可知，相关系数R[x(i),e(i)]定量反映输入信号x(i)与e(i)的相关性大小，x(i)为与噪声相关的估计值，e(i)中存在原始信号分量与噪声分量。在算法初期噪声较强，x(i)与e(i)的相关性较大，即R[x(i),e(i)]的值较大，由式(5)知步长μ(i)亦较大，从而加快算法前期的收敛速度。在算法收敛阶段，输入信号x(i)经自适应滤波器的调整逐渐逼近期望信号d(i)中的噪声分量n(i)，此时误差信号e(i)噪声分量几乎为0，即e(i)与x(i)相关性几乎为0，由式(5)知步长μ(i)也近似为0，从而增加算法收敛阶段的稳态误差，满足了变步长自适应滤波算法的原理。文献[7]SVSLMS算法、文献[10]MVSSLMS算法与本文所提出的C-VSSLMS函数模型如图3所示。

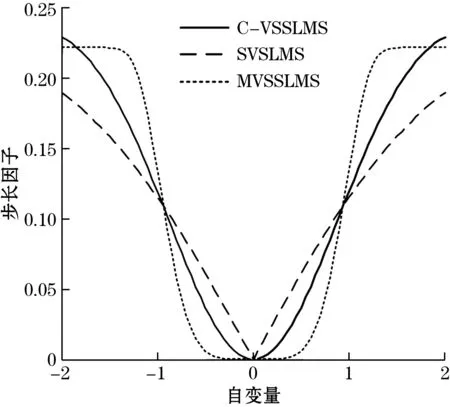
图3 步长因子函数曲线模型

由图3可知，本文算法在前期有较大步长从而加快收敛速度，与算法中期步长衰减相比MVSSLMS所述算法有更加平缓的过渡，从而克服MVSSLMS在中期衰减过快导致收敛阶段步长过小的缺点，在算法收敛阶段，相比文献[11]所述SVSLMS算法，本文算法具备更为平缓的步长变化，从而降低了收敛阶段的稳态误差，使算法具有更高的稳态精度。

综上所述，本文所述改进变步长自适应滤波算法迭代程序为

初始化

(1)x(0)=W(0)=[00…0]；

当i>0时，

(2)滤波：y(i)=xT(i)W(i)；

(3)误差估计：e(i)=d(i)-y(i)；

(5)更新权值：W(i+1)=W(i)+2μ(i)e(i)x(i)。

2.3 基于改进算法的滤波器设计

在对TDLAS系统噪声进行分析的基础上，可以确定自适应滤波器的期望信号主要包括带有气体浓度信息的原始信号、剩余调制幅度(RAM)引起的偏移噪声以及其他噪声3部分，即：

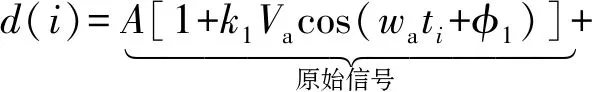
(7)

式中：A为有用信号s(i)的系数；B为非线性部分幅值；C为具备白噪声频谱特性的噪声幅值。

由式(7)可知，系统输入的调制信号为单一频率wa的正弦信号，而非线性部分频率为输入调制信号频率的2倍，其他噪声频率较为复杂但幅值较小，因此三者近似可以作为互不相关信号。且幅值存在A>B>C，因此为了得到线性部分的原始信号，自适应滤波器要必须将剩余两项进行有效滤除。

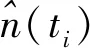
(8)

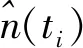
根据以上分析，改进后的基于变步长LMS算法的自适应滤波器的结构框架如图4所示。

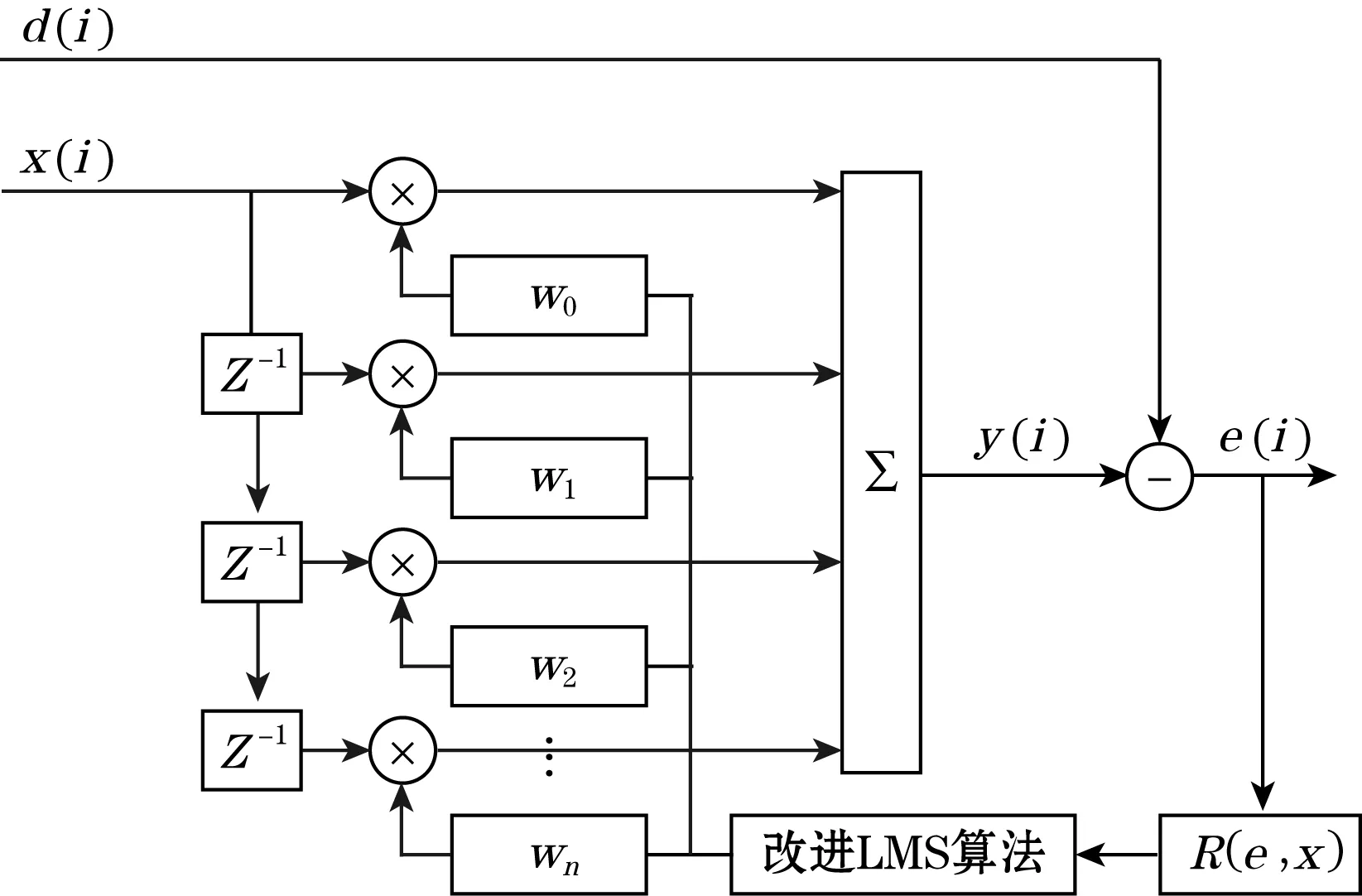
图4 改进的LMS自适应滤波器结构框图

改进的自适应滤波器结构采用横向FIR滤波结构，以式(7)作为滤波器的期望信号，以式(8)作为自适应滤波器的输入信号，即：

(9)

式中S(i)为原始信号。

由式(9)可知，滤波器输入信号x(i)与期望信号d(i)中的噪声分量具备较大相关性，而与原始信号s(i)相关性几乎为0，故以输入信号x(i)与误差信号e(i)的互相关程度大小调整步长，以变步长自适应滤波算法对滤波器的权值系数进行自适应调整，从而输入信号x(i)能够完全预测期望信号中与之相关的噪声分量，使滤波器输出误差信号e(i)达到原始信号s(i)的最优估计，起到良好的去除噪声的效果。

3 仿真分析

3.1 改进算法性能仿真分析

本文利用Matlab对改进算法的滤波效果以及算法收敛性与稳态精度等方面的性能进行模拟仿真分析，并将本文改进算法与所述其余2种改进算法在收敛速度与稳定误差方面进行仿真对比。

首先对所述改进算法的滤波性能进行模拟仿真，滤波器结构采用8阶FIR横向滤波结构，期望信号为幅值为1，频率为10 Hz的正弦信号并混叠均值为0信噪比SNR=5 dB的高斯白噪声，即d(t)=sin(20πt)+n(t)，n(t)=awgn[s(t),5]；滤波器的输入信号为噪声分量的估计值x(t)=0.5n(t)，采样频率为1 000 Hz，采样点数为1 000点，步长调整参数β设置为0.01，α设置为4，滤波器权值初始值设置为0。算法仿真结果如图5所示。

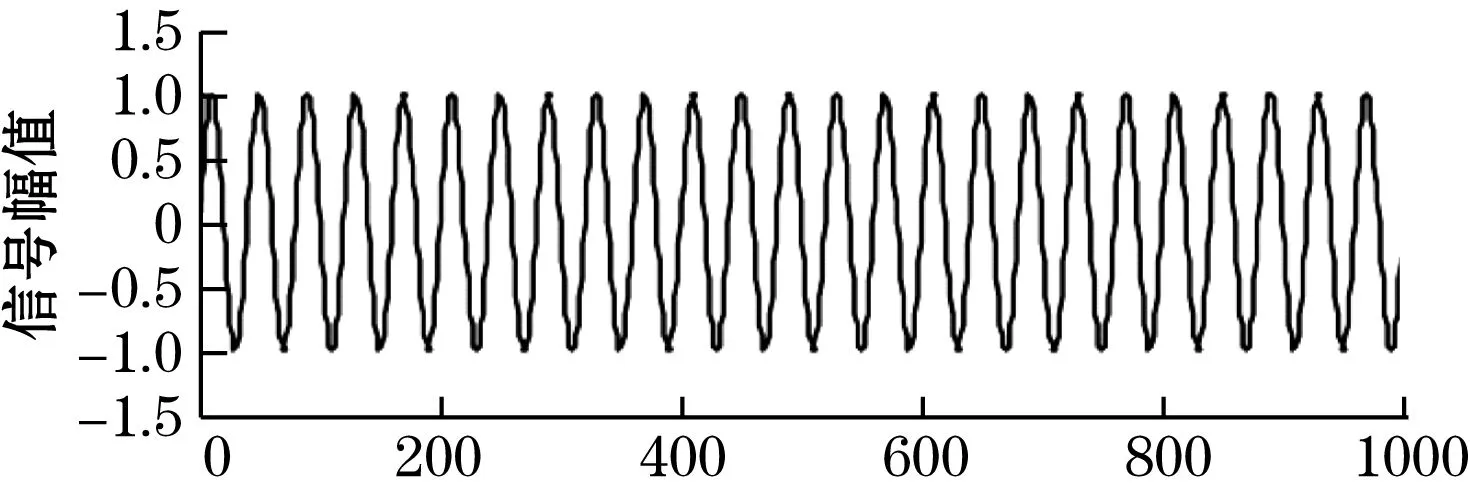
(a)原始信号s(i)波形

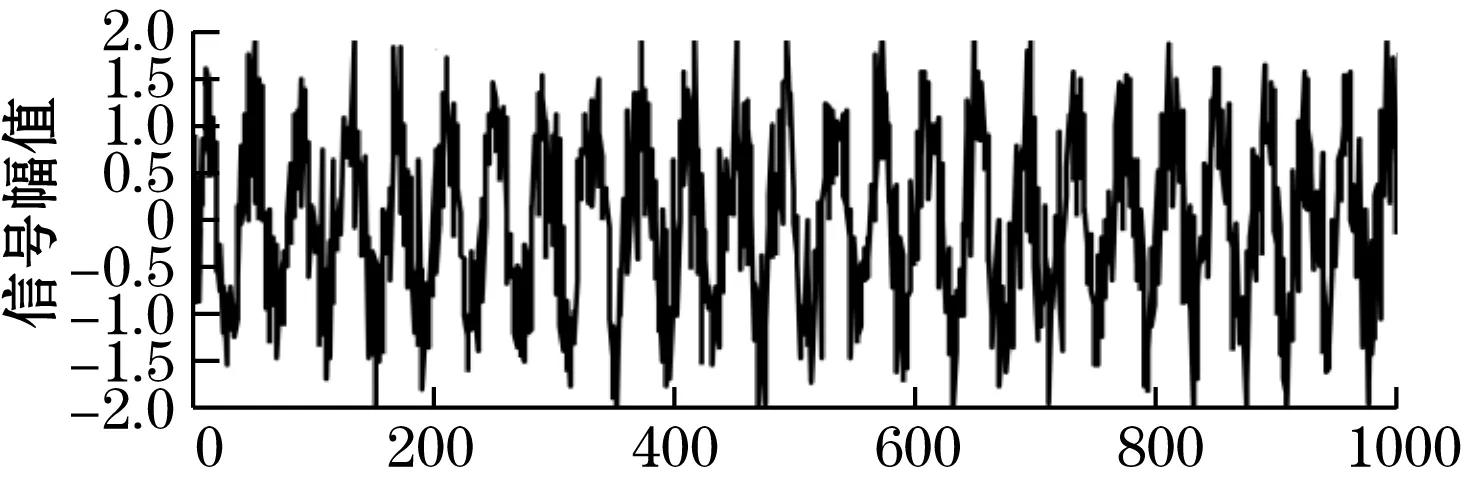
(b)加噪声后的波形

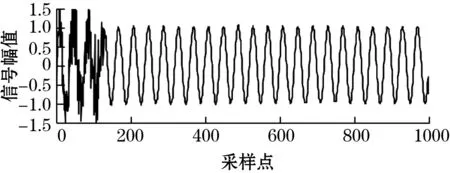
(c)自适应滤波后输出波形图5 本文改进算法在时域中去噪效果

由图5可以直观地展现出本文算法在自适应滤波方面的良好性能，通过对比原始正弦信号与滤波器输出信号波形，定性分析可知由于算法前期处于迭代期，输出信号信噪比较低，而在经过迭代阶段到达稳态后，输出信号基本还原了原始的正弦信号并起到了良好地抑制噪声的作用，因此通过Matlab对改进算法在时域中的滤波性能仿真，基本可以证明本算法具备了较好的滤波性能并且在算法达到稳态之后具有良好的稳定性。

图6所示为本文算法与文献[7]、文献[10]所述2种算法的步长衰减仿真结果。文献[7]中的SVSLMS算法较快地收敛到最小值，并且由于步长对误差信号的变化较敏感，算法收敛后步长稳定性较差；文献[10]中算法初期有较大步长增快收敛性，但中期迅速衰减至最小值，收敛阶段步长虽然平稳但步长衰减过快导致算法收敛略慢；本文算法在算法初期具备较大步长并且较为缓慢地衰减至最小值，使算法能够不影响其稳态精度的同时具备更快的收敛性，与理论分析相符。

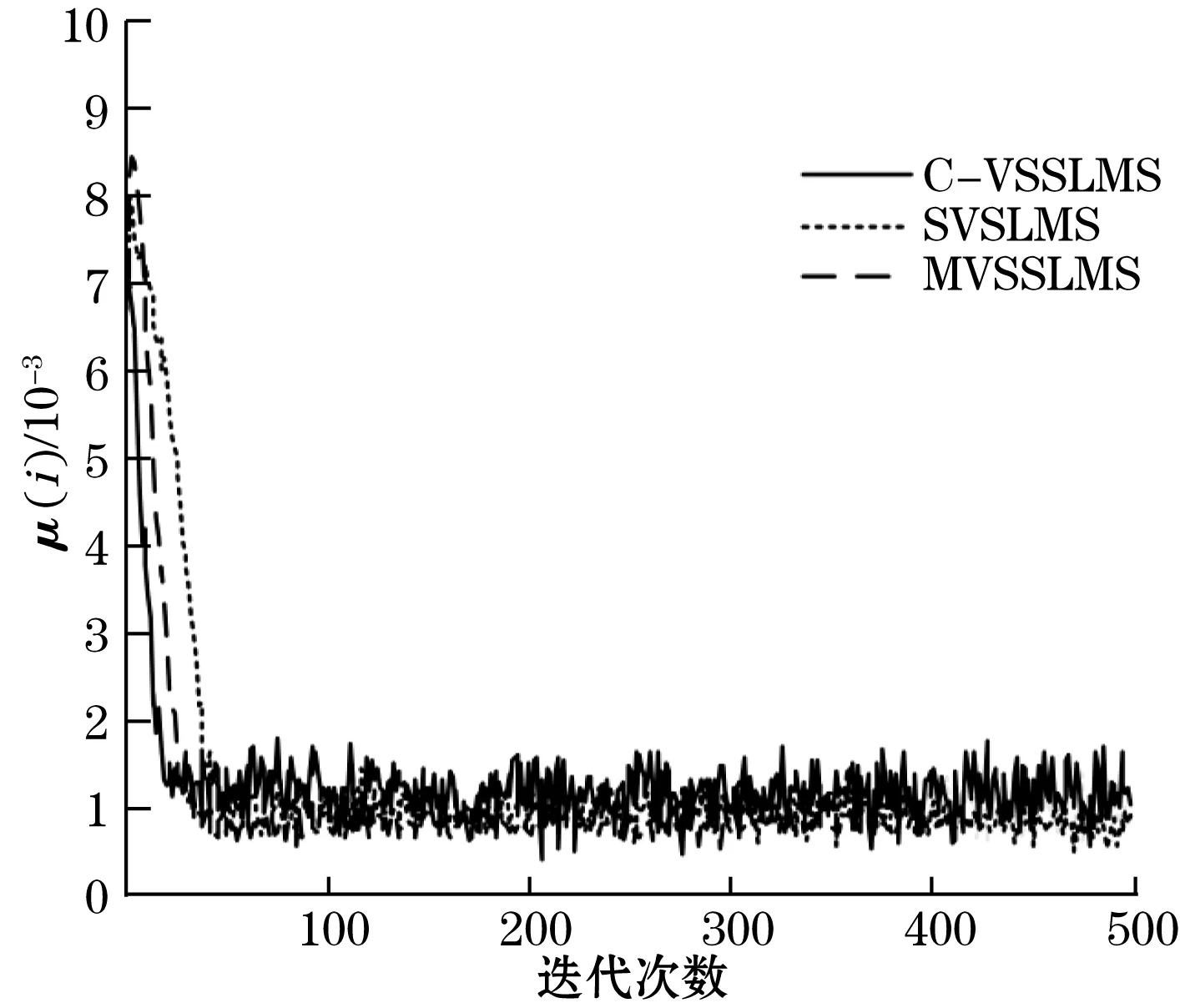
图6 步长与迭代次数关系曲线

为了验证本文所述算法在算法收敛性与稳态误差方面的优势，通过Matlab对算法收敛速度进行仿真，自适应滤波器结构与参数如上述进行设置，依旧采用正弦波混叠高斯白噪声作为滤波器的期望信号输入，输入信号为噪声分量相关的估计值，迭代次数为500次，并将仿真结果与其他算法对比，仿真所得输出误差信号e(i)与正弦信号s(i)的均方误差与迭代步长的关系曲线图如图7所示。

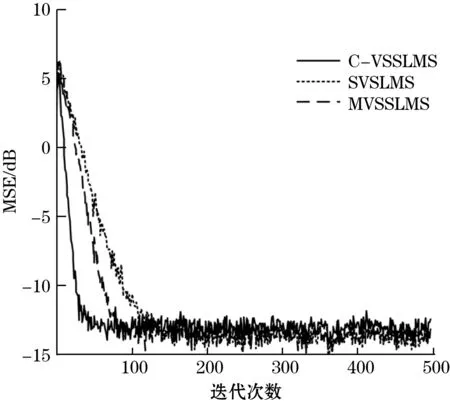
图7 均方误差与迭代次数关系曲线

从图7可以直观地看出本文算法在收敛速度方面明显优于其他2种算法，相比SVSLMS算法，改进算法在算法收敛阶段具备了更好的稳态误差，相对文献[10]本文算法虽然在临近收敛阶段稳态误差起伏略大但收敛速度要比它快近30次迭代次数。因此进一步说明了本文改进算法不仅在滤波方面具备良好的性能，并且在算法的收敛速度与稳定性上也同样具备优越性。

3.2 改进算法应用仿真分析

为了验证本文变步长自适应滤波算法在基于TDLAS痕量气体检测系统中的去除噪声的效果，本文依据朗伯-比尔定律以及谐波检测理论，并基于实际TDLAS系统结构，通过Matlab软件的Simlink模块库对基于自适应滤波算法的模拟TDLAS系统进行建模仿真与分析，仿真系统主要包括光源模块，洛伦兹线型函数仿真模块，气体吸收仿真模块，光电探测器模块与基于锁相放大器的数据处理模块，仿真系统整体结构图如图8所示。

图8 TDLAS仿真系统结构图

系统仿真中低频扫描信号采用频率f为1 Hz、幅值A为1 V的锯齿波，高频调制信号采用频率ωa为30 kHz，幅值Va为0.05 V的正弦信号，二者叠加作为激光调制信号输入，气体吸收谱线中心值V0为6 731 cm-1常数模块，光强输入I0为5 mW常数模块，模拟气体吸收线型采用洛伦兹线型，模拟气体吸收池常数(压强、光程长等)的乘积模块为0.001，调制深度为2.2，随机噪声n(i)为均值为0、方差为0.01的高斯白噪声，自适应滤波器结构设置与信号输入均采用前面滤波器设计部分所述，最后对系统进行仿真，光电探测器仿真模块输出信号如图9所示。

由图9可知，光电探测器输出信号包含原始信号、非线性调制部分以及系统噪声，当信号处理单元为普通FIR抗混叠滤波器时，信号经采样后直接由双路正交锁相放大器解调二次谐波信号，输出的二次谐波信号如图10所示，当输出信号首先进行自适应滤波处理后经锁相放大器解调输出的二次谐波信号如图11所示。

由图10所示输出的二次谐波信号虽然经过低通滤波器去除了大部分噪声，但残留噪声依旧对线型影响较大，甚至导致二次谐波信号主峰畸变，影响对所测气体浓度的反演。通过对光电探测器模块输出信号进行自适应滤波后，锁相放大器的输出二次谐波信号如图11中实线所示，与虚线理想二次谐波信号基本吻合，通过计算降噪前后2次输出信号信噪比可知，经过自适应滤波器的降噪作用，锁相放大器输出信号的信噪比提升了14.75 dB，因此表明基于变步长自适应滤波算法的数字滤波器能够有效提高系统输出二次谐波的信噪比。

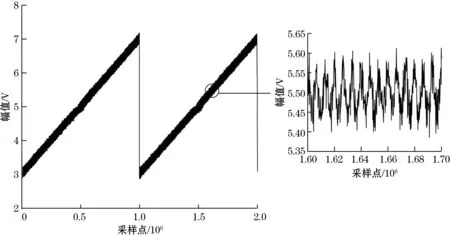
图9 光电探测器模块仿真输出

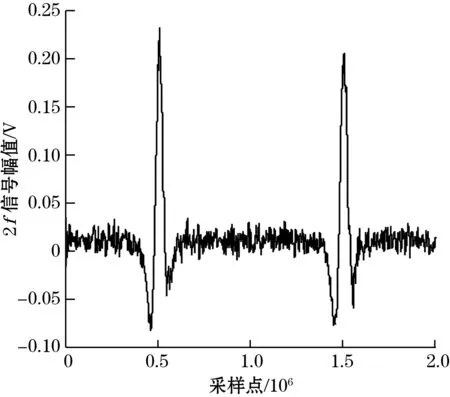
图10 含噪声的二次谐波信号

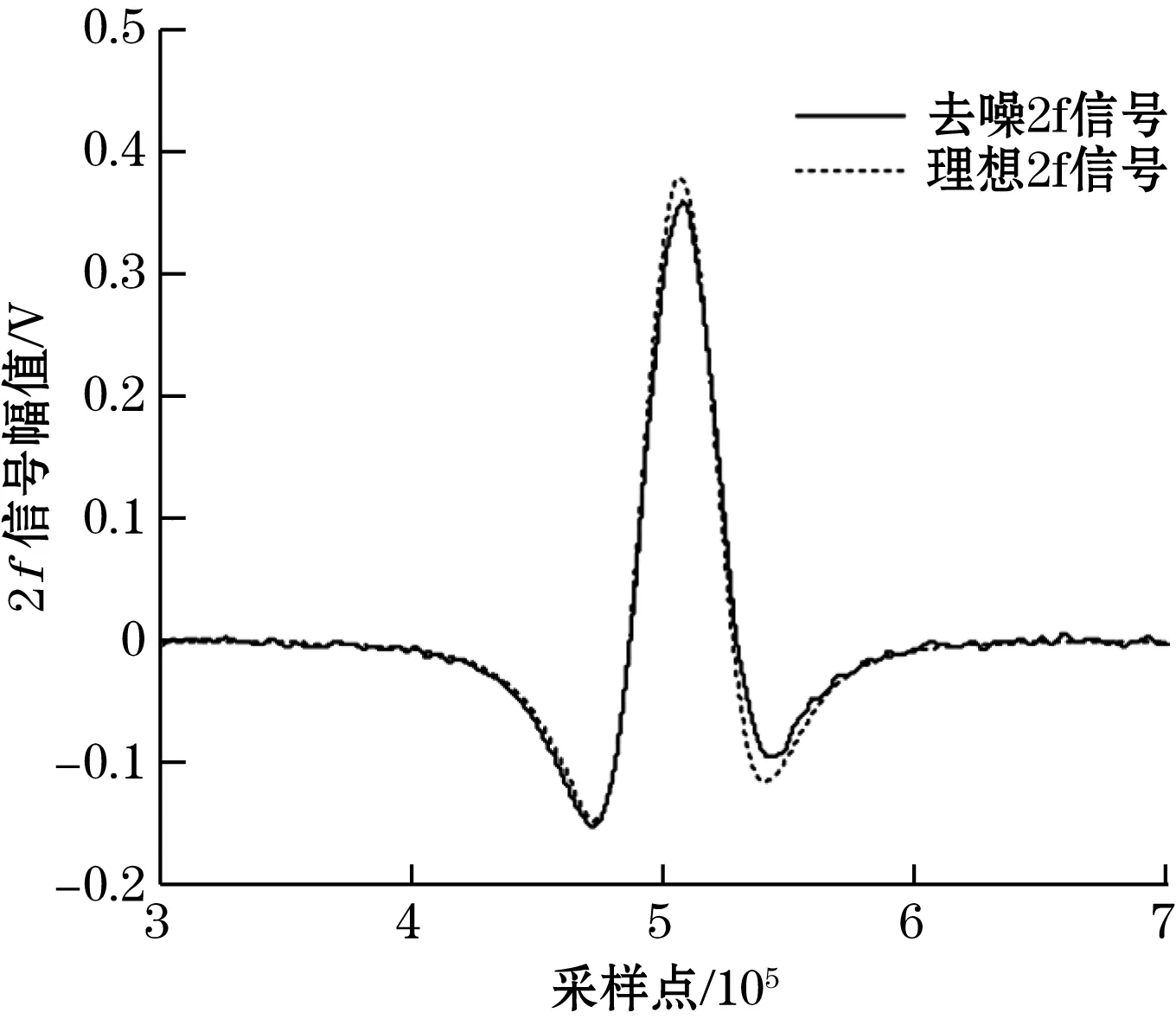
图11 经自适应滤波后输出的二次谐波信号

4 结论

本文旨在提升TDLAS痕量气体检测系统输出二次谐波信号信噪比，设计基于改进变步长自适应数字滤波系统，对系统中剩余幅度调制引起的偏移噪声以及随机噪声起到良好的抑制作用。算法中采用误差信号与输入信号相关性大小为自变量，并进行应用性仿真实验，测试结果表明TDLAS仿真系统输出信号信噪比明显提升，能够很大程度抑制非线性调制所引起的二次谐波线型畸变，达到实验预期去噪效果。应用仿真对后期实际TDLAS检测系统的信号处理部分植入自适应数字滤波算法提供了理论支持，并且本文算法适用性强易于硬件实现，具备很广阔的实际应用前景。