基于改进SIFT的时间序列图像拼接方法研究
卢 鹏,卢 奇,邹国良,王振华,侯 倩
上海海洋大学 信息学院,上海201306
1 引言
图像拼接融合,是指将同一场景的两幅或多幅相互间存在重叠部分的图像进行空间匹配对准,融合处理后形成信息更完整和更全面的图像[1-4]。有别于多源遥感图像融合和多聚焦方式融合,拼接融合主要用于处理同种图像传感器以相同成像方式,在离散时刻拍摄的图像(或多个同种传感器在同时、不同角度拍摄的图像),即时间序列图像。拼接融合处理后的图像能够有效弥补单传感器无法充分获取目标信息的缺陷,解决图像信息量不足的问题,更适合视觉感知或计算机处理[5]。目前,图像拼接融合技术被广泛应用在智能交通、虚拟现实技术等领域。图像拼接融合的内容主要包括图像配准、图像拼接和融合两部分。目前,主要有三种图像配准方法:灰度信息配准方法[6]、特征配准方法[7]和变换域配准方法[8]。其中,基于灰度信息的配准方法是根据图像中的灰度统计信息来确定图像的相似度,计算量大,且对噪声十分敏感;基于变换域的配准方法主要通过傅里叶变换的方法来实现,图像的平移、旋转、缩放等操作在频域上都有体现,具备一定程度的鲁棒性,但是其适用的范围较小,处理信息量大,计算复杂度高。特征配准方法适用范围广,计算速度较快,且具有较高的鲁棒性,是目前最常用的配准方法。常见的特征配准方法有:Moravec[9]、Harris[10]、Harris-Laplacian[11]、SIFT[12-13]。其中尺度不变特征变换匹配算法(Scale Invariant Feature Transform,SIFT)因其不受尺度、旋转、光照等因素的影响,具有很强的稳定性,成为目前使用最广泛的特征配准算法之一。
近年来,研究学者们针对SIFT 算法存在的问题,进行了很多改进。文献[14]针对SIFT 特征描述符维数较高,计算量大这一问题,将主成分分析法(Principal Component Analysis,PCA)与SIFT结合,提出了PCA-SIFT,对特征描述符进行降低维数的处理,达到提高算法运行速度的目的;冯文斌等人[15]采用分级放射分区的方法构建64 维特征描述符;张勇等人[16]将SIFT 和Harris 结合,在提取SIFT 特征的过程中加入Harris 角点算子,并采用圆形窗口构建48维特征描述符。上述改进算法大多是针对SIFT 特征描述符的降维,当SIFT 提取到的特征点数量很大时,降维的效果并不明显,且极易造成错误匹配。
在此基础上,本文提出了一种减少SIFT 算法特征点个数的方法,并采用12 环的圆形窗口构建特征描述符,既减少了特征点个数,又对特征描述符进行了降低维数的处理,从而大大减少了配准的运行时间。然后用RANSAC 去除错误的配准点对,并采用渐入渐出融合算法将两幅图像拼接融合成一幅更完整的图像,以增强图像的边缘和纹理信息。为了验证算法的融合效果,本文对融合后的图像进行了局部区域分块检测,并从信息熵、边缘强度和峰值信噪比等几个指标与融合前的图像进行了数值化比较。实验结果表明,本文算法具有较高的鲁棒性,运算速度快,且具有较好的融合效果。
2 SIFT算法
SIFT 算法通过构造图像的尺度空间,并检测图像的极值点,从中确定关键点(key-point),以关键点为中心取其邻域,构建SIFT特征点描述符,最后根据得到的特征描述符对图像进行配准。
(1)尺度空间关键点检测
SIFT算法利用高斯函数构造图像的高斯金字塔,然后用高斯金字塔中上下两个相邻高斯尺度空间上的图像差值来表示差分高斯(Difference of Gaussian,DoG)的响应值图像。DoG的响应值图像可以表示为:

其中,G(x,y,σ)是高斯核函数:

其中,I 是原始图像;L 为图像的尺度空间;σ 的大小决定不同尺度,σ 越大则图像越模糊。如图1为差分高斯金字塔。

图1 差分高斯金字塔
建立差分高斯金字塔后,初步检测DoG 局部极值点,并精确定位其空间位置和尺度。由于初步搜索到的候选极值点中包含对比度较弱、边缘响应较强等不稳定的点,因此采用曲线拟合等方法剔除候选点中不稳定的极值点。剔除不稳定的关键点后,计算剩余合格的关键点邻域像素的梯度方向分布特性,以此确定关键点的方向,其中部分关键点的方向包含主方向和辅方向,最后得到SIFT特征区域。
(2)局部特征描述
对计算后的关键点进行描述,得到局部特征描述符,包括校正旋转主方向、生成描述子和归一化处理三个部分。再根据关键点的方向调整坐标轴,使二者保持一致后,在每个关键点对应的尺度空间中,选取以关键点为中心、大小为16×16 的方形窗口作为一个邻域范围,将该范围分成4×4 个子区域,计算每个子区域上像素的梯度幅值和方向,从而得到关于的梯度信息的累计直方图,生成包含8 个方向向量信息的种子点。如此,一个关键点可生成4×4×8=128 维的SIFT 特征描述符。每个特征描述符不仅包括关键点,也包含了关键点周围对它有贡献的像素点,抽象表示了该区域的图像信息,具有独特性。最后,对特征描述符进行归一化处理,消除光照变化的影响。
3 改进的SIFT算法
基于SIFT 算法存在的问题,本文对局部极值点的检测方法和特征描述符的构建进行了改进,减少了关键点个数,并降低了特征描述符的维数,在保证算法准确性的前提下,提高了算法的运算速度。
3.1 特征描述符的构建
3.1.1 改进的极值点检测方法
SIFT算法中,在尺度空间中检测极值点时,每一个像素点都要和其同一尺度相邻的3×3-1 个像素点以及上、下相邻两个尺度的3×3×2个像素点,即总共26个相邻像素点进行比较,从而得到局部极值点。但是由于一般图像帧信息复杂,导致检测到的特征点数量过多,容易产生错误匹配,且计算量过大,耗时久。本文改进了极值点的检测方法,在极值点检测阶段,扩大了每个像素点的比较范围,扩大了极值点的生成区域,从而使得极值点的数目得到减少,以去除部分错误匹配点对,降低错误匹配几率,从而提高关键点质量。为了选取合适的检测范围,本文分别对3×3、5×5、7×7和9×9这4极值点检测范围进行了实验,以对比检测得到的关键点数量和运行时间,实验结果见表1。
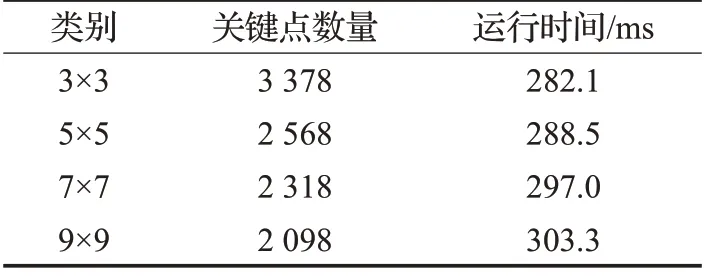
表1 极值点检测范围部分对比实验结果
由表1 可知,随着检测范围的不断扩大,检测得到的关键点数量不断减少,检测部分的运行时间不断增加。根据实验结果,综合考虑算法的运行效率,本文选取5×5的区域作为检测范围,即总共74个相邻像素点进行比较,从而减少关键点数目,在后续配准算法中减少算法的时间开销。从整体算法的运行时间来看(见本文第4章),扩大检测范围能够减少算法整体的运行时间。改进的SIFT的尺度空间局部极值点检测如图2所示。
则以每个像素点为中心像素点,分别以3×3、5×5的局部区域范围进行极值点检测,在列数为n 个像素、行数为m 个像素的图像中,二者每层极值点遍历的采样比见公式(3):
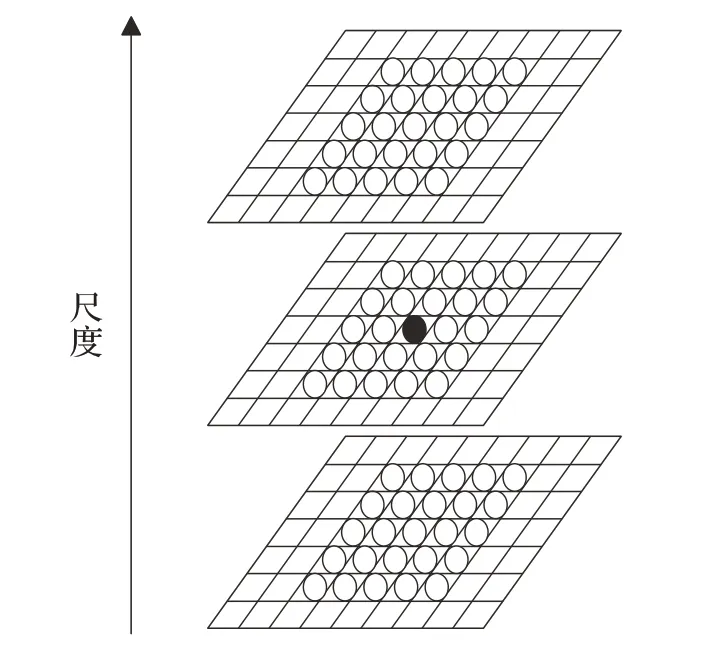
图2 5×5区域的SIFT的尺度空间局部极值检测
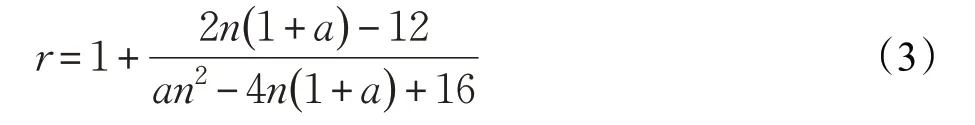
其中,m=an。针对本文对局部极值点检测范围的改进,与传统SIFT 算法进行了3 组对比实验,得到待确定的极值点数量(包含不稳定的点)和剔除低对比度和边缘响应不稳定等不合格的点后的关键点数量,如表2所示。

表2 极值点检测方法改进前后分析比较
由表2可见,改进后的局部极值点检测减少了关键点数目,从而减少了描述子生成的时间开销。
3.1.2 改进的特征描述符
SIFT 算法在对特征点进行描述时,首先要对坐标轴进行调整,将坐标轴旋转到关键点的方向,使二者的方向保持一致,以确保旋转不变性。由于圆具有良好的旋转不变性,Tang 等人[17]提出了在构建SIFT 特征描述符时,采用圆环形区域取代原SIFT 中的方形区域。因此,本文采用圆环形区域来构造特征描述符,无需考虑坐标轴是否与特征点的主方向相同,使得特征描述符自身具有旋转不变性,从而免去了调整坐标轴方向的步骤,故减少算法复杂度,节省了时间开销。
为了更合理地选取圆环形的环数,本文以关键点为中心,依次选取半径为8~20的同心圆区域,分别构建半径为8~20共13种SIFT特征描述符,并分别计算其时间和匹配正确率,进行对比实验,结果如图3、4所示。

图3 圆环形区域取8~20环的计算时间

图4 圆环形区域取8~20环的匹配正确率
根据实验结果,本文取半径为12 的同心圆区域。由于环形区域对特征点的影响与其距离特征点的大小有关,即与特征点之间的距离越近的环形区域的像素对特征点的描述贡献越大,故本文采用(3,3,2,2,1,1)的环数构造,即将距离特征点最近的最内环设置为3 个环,而距离特征点最远的最外环设置为1个环,如图5所示。计算梯度累加直方图时,以36°为单位计算每个环上的10个方向上的梯度累加直方图。本文借鉴文献[18]的方法,结合灰度差累加直方图,将其引入SIFT 算法中,计算每个环的灰度累积值,并将子环区域的灰度累加值作为一维特征向量,引入特征描述符的构建,从而减少由灰度变化引起的错误匹配。最后,对每个子环内10个梯度累加值进行排序,并对特征向量进行归一化处理,本文最后得到78维的特征描述符。
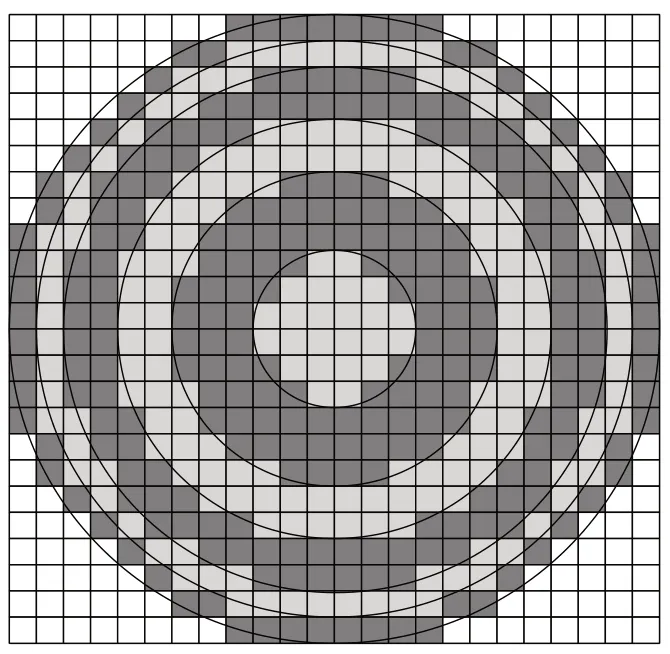
图5 改进的特征描述符环构造
3.2 特征描述符配准
3.2.1 特征点初次配准
提取到两幅图像的特征点后,分别得到两幅图像的特征描述符的集合,采用K-D 树的最优节点优先BBF搜索策略对两个特征向量集进行搜索最近似特征向量。计算图像1中的特征点与图像2中距离其最邻近的特征点间的距离和次邻近特征点的距离的比值,得到配对的关键点描述子d(m,n)若满足:

其中,threshold 为配准阈值。阈值大小的选取决定了配准点对的数量和质量。Lowe 建议设置为0.4~0.8 配准效果最佳。若设置的threshold 小于0.4 会导致配准点对数目较少;而设置的threshold 大于0.8则会存在大量错误的配准。本文设置配准阈值为0.58。
3.2.2 消除错误配准
RANSAC[19]是一种参数估计算法,其主要思想是:从样本数据集中随机选取一个子集,对该子集进行参数估计,从而确定参数估计模型。将所有样本数据集带入该模型,对其进行验证,根据损失函数得到一致性集合。根据样本数据集中符合一致性集合的点集数量大小,确定该模型的正确性。通过多次的假设与检验,最后得到一个全局最优的模型参数。在SIFT 中使用RANSAC算法,去除错误的配准,从而提高算法的匹配正确率。
3.3 图像拼接融合
在由两幅图像的特征点描述符对图像进行配准后,需要根据图像间的空间变换关系对图像进行拼接融合。由于两幅待拼接融合的图像之间可能存在光照不同、几何校正差异等情况,会导致拼接融合后的图像存在明显的拼接缝隙。因此,采用合适的图像融合方法进行处理,使得拼接后的图像的灰度信息保持一定的连续性,消除拼接缝隙,就显得十分重要。传统的加权平均融合算法的权重值的选取是固定的,这就使得很难消除由于两幅图像光照差别较大等原因引起的拼接缝隙,导致两幅图像拼接融合的效果相对较差。为了使拼接融合后的图像边界部分自然过渡,无明显的结合痕迹,目前常用渐入渐出融合算法[20]进行图像自然过渡,消除拼接缝隙。与传统的加权平均融合算法不同,渐入渐出融合算法在两幅图像的重叠区域,使权重d 随着像素点位置的变化呈线性变换,以此保持图像的灰度信息能够平滑过渡,消除拼接缝隙,提高图像融合质量。权重d 的变化规律见公式(5):

其中,j 表示像素点的列数,L 和R 分别表示重叠区域的左边界和右边界。
假设f1( x,y )、f2( x,y )是两幅待拼接的图像,f( x,y)是融合后的图像,则拼接融合后的图像可表示为:

其中,d1、d2表示权重值,取值与重叠区域的宽度有关,且d1可由公式(6)计算得到,则d2=1-d1二者的取值范围是0 <d1,d2<1,在重合区域中,d1由1渐变为0,d2由0渐变为1,因此完成了在重合部分中由f1平滑过渡到f2的过程,从而实现图像的无缝拼接。
为更好地避免了重影,消除拼接缝隙,本文采用罗永涛等人[21]提出的一种最佳缝合线与改进的渐入渐出法相结合的图像拼接融合算法(如图6),在一定程度上提高了图像拼接融合的质量。

图6 渐入渐出融合权重变化规律
3.4 融合效果的评价方法
由于全局检测不能有效体现图像拼接融合后的细节信息,本文对拼接融合前后的图像,从边缘强度、信息熵、峰值信噪比等方面进行局部区域分块检测,评价图像拼接融合的效果。
分别选取进行拼接融合的两幅图像的重合区域以及融合后图像的该部分进行实验分析。若图像的重合区域的列和行分别为为n 和m 个像素,则每个小块的大小为长br和宽bl:

其中,r 和l 是图像重合部分的长和宽分别可以分成的份数:
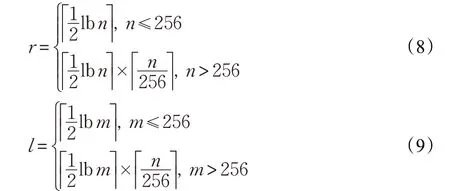
计算每个小块边缘强度、信息熵、峰值信噪比。实验见下文实验结果及分析。
4 实验结果及分析
本文实验平台为Matlab R2015a,运行环境是CPU为Intel Core i5-6500 3.20 GHz,内存为4 GB的64位的Windows10操作系统,将500组图像进行拼接融合实验,由于篇幅限制,本文选取A~E共5组实验,如图7~11所示。

图7 A组实验待拼接融合图像

图8 B组实验待拼接融合图像

图9 C组实验待拼接融合图像

图10 D组实验待拼接融合图像

图11 E组实验带拼接融合图像
4.1 SIFT特征点运算时间实验结果及对比分析
本文采用SIFT、PCA-SIFT 算法以及文献[16]改进的SIFT算法和本文算法对5组图像进行多次实验,统计其平均匹配正确率和运行时间,结果如表3所示。可以看出,本文的算法在保证较高的匹配正确率的情况下,能够有效减少算法匹配时间,降低时间复杂度。

表3 本文算法与其他算法的匹配正确率和运行时间的对比结果
在图像配准后,使用渐入渐出融合算法来拼接融合待拼接图像,得到A~E 共5 组实验的拼接融合后的图像,如图12~16所示。

图12 A组实验拼接融合图像

图13 B组实验拼接融合图像

图14 C组实验拼接融合图像

图15 D组实验拼接融合图像

图16 E组实验拼接融合图像
4.2 融合效果对比分析
针对全局检测图像不能有效体现图像拼接融合后的细节信息,本文对拼接融合后的图像进行局部区域分块检测从边缘强度、信息熵、峰值信噪比等方面来评价图像拼接融合的效果。
如图17 所示,选取拼接融合后的图像和待拼接图像的重叠区域,根据公式(7)~(9)进行局部区域分块。在A组实验中,取图像的重叠区域,其大小为380×640,根据公式(7)~(9)将其分成列为38个像素、行为42个像素的局部图像,共150 个小块局部图像,评价其拼接融合效果,实验结果如表4所示。由表4可以看出,采用本文算法拼接后的图像的信息熵更大,即图像信息更丰富,边缘强度得到增强,峰值信噪比较高,即有效抑制了噪声。
5 结束语
本文针对SIFT 算法存在的问题,提出了一种基于改进的SIFT的图像拼接融合算法。本文改进了特征点的检测方法,扩大了极值点的检测区域范围,减少了关键点的数量;改进了特征点描述符的构造方法,并降低了特征描述符的维数;使用渐入渐出加权图像融合算法进行图像拼接融合,整个算法提高了图像拼接融合的速度。图像质量关键参数的局部区域分块检测表明,在具有良好的拼接质量的前提下,本方法具有快速、可靠、有效的特点。改进后的SIFT算法虽然有效降低了运行时间,但算法的匹配正确率提高不是很明显,下一步将在此研究基础上,提高算法匹配正确率。

图17 均分成每小块为38×42的局部图
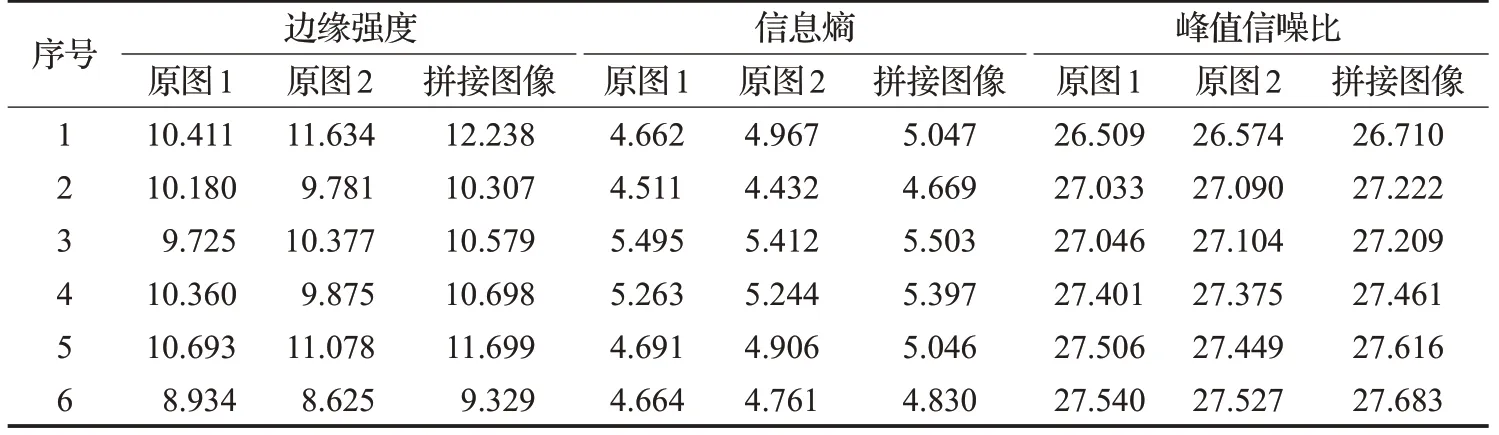
表4 图像拼接融合效果数值分析(部分)

