球头刀铣削表面粗糙度的研究
原恩桃, 邵 兵
(上海电机学院 机械学院, 上海 201306)
零件的表面粗糙度是衡量一个零件表面加工质量的一项技术要求,对于零件的配合、耐磨性、抗腐蚀性及密封性等都有显著影响。影响表面粗糙度的因素主要有工件材料、切削参数、机床性能以及刀具的材料几何参数等。文献[1-5]通过试验的方式研究了切削速度、进给量、背吃刀量与工件表面粗糙度之间的关系。雷小宝等[6]对表面粗糙度的影响因素进行了极差分析,得出进给速度对表面粗糙度影响最大。姚倡锋等[7]利用涂层硬质合金刀具对TC11进行了高速切削实验,得出进给量、切削深度及切削速度对表面粗糙度的影响规律。
在实际加工零件时,切削深度、进给量及主轴转速等都是预先给定且在切削过程保持不变的,因此,如何将影响表面粗糙度的各因素组合优化,从而得出最佳表面质量值,文献[8-11]对表面粗糙度的计算给出了预测模型及优化。本文从表面粗糙度的计算公式开始得到表面粗糙度与切屑厚度之间的关系,从而进一步探讨表面粗糙度与切削深度和进给速度之间的规律,并进一步通过试验探讨了各因素对表面粗糙度的影响。
1 表面粗糙度产生机理
1.1 残留高度产生机理
在曲面加工中,残留高度主要是由刀具沿着刀具路径移动,留在零件表面未去除材料形成的[12-14]。如图1所示,设定:P为刀触点,R为曲面半径,θa为两个半径线之间的夹角,n为P点处法向矢量。走刀行距dw与残留高度h有着密切的关系。根据图2(a)可得
(1)
式中:r为刀具半径;kb为加工表面沿切削进给方向的法曲率。

图1 曲面加工模型
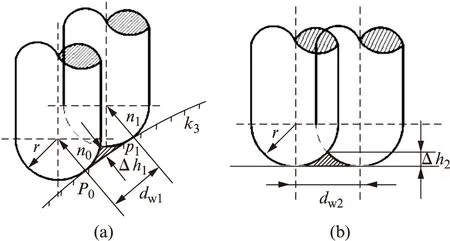
图2 加工参数之间的关系
采用截平面法生成刀具轨迹时,由于kb的计算比较困难,在实际加工中通常采用一个平面逼近两相邻刀轨之间的曲面,如图2(b)所示,即走刀行距视为截平面之间的法向距离,此时残留高度可以用下式描述为
(2)
2.2 表面粗糙度的计算
由于残留高度的存在,导致零件经过机械加工后的表面会留有许多高低不平的凸峰和凹谷,该微观几何形状称为表面粗糙度,如图3所示。定义Ra为表面粗糙度,即
(3)
式中:L为取样长度。

图3 表面粗糙度
对图3进行局部放大得图4,当h′ E(A′)=tanθ(2yE(h′)-E(h′2)) (4) 图4 表面粗糙度的计算 当h″>ycl,可得出 (5) 式中:E()表示区域面积。 由于ycl要保证中线上下区域面积相等,即 p′E(A′)+2p″E(A″t)=p″E(A″b) (6) 式中:p′和p″为一权因子,其计算方法可参考文献[15]。 p与切屑厚度h密切相关,经过一系列的推导,可以得到 (7) 此时取样区域面积表达为 E(Ra)=p′E(Ra′)+p″E(Ra″) (8) 式中: 将式(4)和式(5)代入式(8),可得 0.5E(h″)]-ycl (9) 将式(7)代入式(9)并经过计算简化,得到表面粗糙度取样区域面积与切屑厚度的关系为 E(Ra)=0.37E(h) (10) 由上式可知,表面粗糙度与切屑厚度之间具有非常简单的影响关系。当采用球头刀铣削时,每齿进给量是常数,而切屑厚度根据切削深度和进给速度在不断变化着。 在稳态切削条件下,通过改变切削深度、进给速度,测量不同参数组合所得的粗糙度数值,在三维形貌仪下观测其微观形貌,并分析切削参数对表面粗糙度的影响规律。 该次试验对如图5所示的刃口零件采用FANUC精密加工中心机床进行加工,毛坯材料为45#钢,刀具选用直径为12.5 mm的高速钢铣刀,主轴转速为800 r/min,切削深度采用1~6 mm,当切削深度为1、2、4和6 mm时,采用不同的进给速度加工,加工过程如图6所示。 图5 试验零件 图6 零件的加工 零件完成加工后,对图5所示的零件曲线部分选取测量点,每组实验条件下对该测量点的数据均进行两次测量,取其平均值得到实验值。试验数据见表1。 表1 试验所得数据 从试验数据看出,采用球头刀对零件进行加工,当进给速度不变时,表面粗糙度随着切削深度的增加而增加(见图7),当切深较小时,表面粗糙度值较小,但是切深过小将导致切削时间较长,加工效率低。当切削深度不变时,随着进给速度的增加其表面粗糙度的值先减小然后再增加,这表明进给速度不是越大越好,而是有一个最优值,因此在实际加工要慎重选择。本文的试验值和理论值虽然有一定差距,但基本接近。因此,本文所给出的计算公式可以采用。对于本文所选择的加工零件,当切削深度为2 mm,进给速度为700 mm/min时,表面粗糙度达到最优。 图7 切削深度与表面粗糙度的关系 探讨了零件铣削过程中一些加工参数对表面粗糙度的影响。从理论上探讨了表面粗糙度对零件表面质量的影响,根据表面粗糙度的生成机理推导了其理论计算公式。通过试加工的方法,采用不同的参数数据组合,对加工后的零件采用三维形貌仪测得表面粗糙度,并将公式计算出的理论值与试验值作比较。研究证明,计算公式和加工方法均是可行的。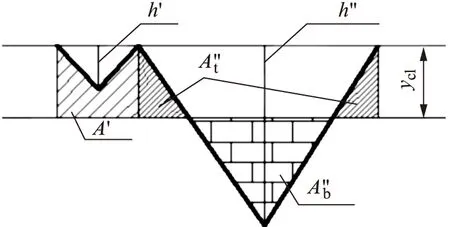
2 试验数据与分析
2.1 试验条件
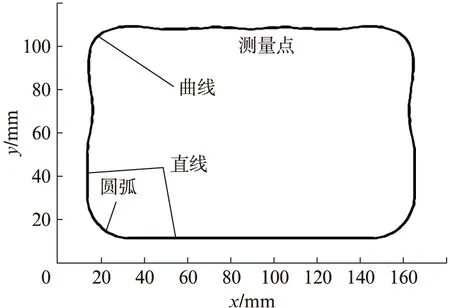

2.2 数据测量
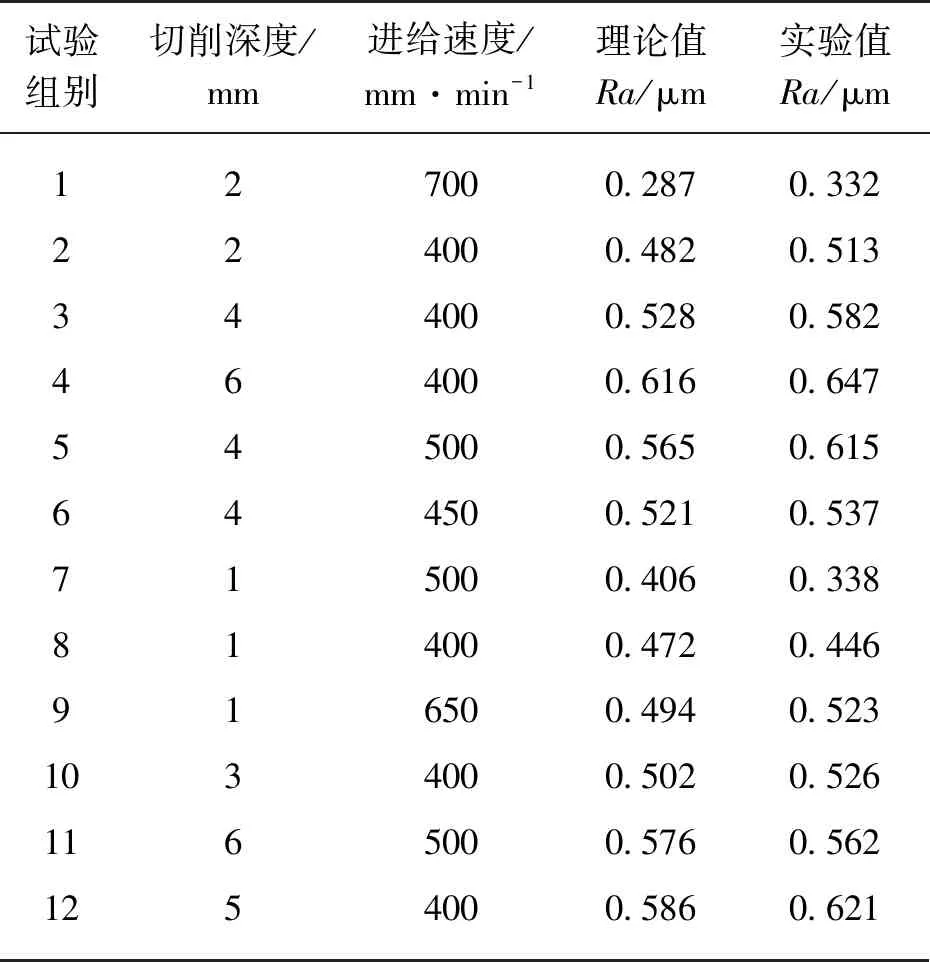
2.3 数据分析

3 结 论

