改进鲸群优化子空间匹配追踪的稀疏解混算法

贾志成，郑 笑，郭艳菊，陈 雷

1)河北工业大学电子信息工程学院，天津 300401；2)天津大学精密仪器与光电子工程学院，天津 300072；3)天津商业大学信息工程学院，天津 300134

高光谱成像技术是利用成像光谱仪分别在不同的波段对同一场景进行成像，因而存在大量混合像元.为实现对地物的精准分类，需对图像进行混合像元的分解，即高光谱图像解混[1].从混合图像中求解出包含几种单一特征地物(端元提取)，并估计其所占混合像元的比例(丰度系数).目前，高光谱混合模型分为线性混合模型和非线性混合模型[2].线性高光谱模型物理原理简单以及计算量小，是目前备受青睐的高光谱图像解混模型[3].

传统线性高光谱图像解混方法是在没有包含任何先验知识下假设纯像元的存在.为摆脱此局限，近年来，随着压缩感知以及稀疏表示理论的快速发展，有学者将稀疏性约束引入到高光谱图像处理中，以期更好地挖掘先验信息[4].由于光谱库中的端元数远大于混合像元中的实际端元数，仅少数端元谱线对应的丰度值为非零.因此，基于光谱库的稀疏解混无需假设纯像元的存在.高光谱图像稀疏解混算法主要有凸优化方法和贪婪算法[5].凸优化方法虽然能够精确地重建所有稀疏信号，但是重建速度慢，难以解决大尺寸图像的重建问题[6].贪婪算法利用匹配追踪(matching pursuit, MP)[7]和正交匹配追踪(orthogonal matching pursuit, OMP)[8-9]算法对光谱库进行提取,再利用最小二乘法进行丰度估计.但是，这两种算法在端元选择机制中多易陷入局部最优，备选端元进入端元支撑集则永不会被删除.为此，有学者提出联合正交匹配追踪(simultaneous orthogonal matching pursuit, SOMP)[10]、子空间匹配追踪(subspace matching pursuit, SMP)算法[11]及其改进算法[12-13]，使选择的端元接近于全局最优.但SMP算法在光谱库寻找与混合像元相关度最高端元过程中，每一次循环不限制数量的把几个可能的端元都提取出来，构成端元集，且不可以更正之前循环中选择错误的端元，因此，对于已选的端元存在冗余现象，影响丰度的估计精度.

为解决端元冗余问题，LI等[14]基于子空间匹配追踪算法提出融合了广义Dice系数法的解混方法.近年来，又有学者将仿生智能优化应用到高光谱图像解混中，并取得了优异效果[15-19].然而，这些方法目前主要还是利用高光谱传统模型进行求解，若进一步应用到稀疏解混模型，可达到更好的解混效果.

为此，本研究提出基于改进鲸群优化算法的子空间匹配追踪(improved whale optimized subspace matching pursuit algorithm, IWOSMP)算法.算法对鲸群优化算法(whale optimization algorithm, WOA)[20]进行了改进，通过引入非线性种群控制参数和进化策略，改善了原WOA收敛速度慢和精度低的问题，基于SMP解混，采用改进的WOA对高光谱图像的每个像素点进行解混，以稀疏性约束为目标函数，利用WOA的全局搜索能力来实现对丰度系数的精确估计，在保证重构误差最小的前提下，去除与实际图像相关性较低的端元，使入选的端元集更精确，进一步提高解混精度.

1 高光谱图像稀疏解混模型

稀疏解混模型是假设观测到的混合光谱可表示为线性组合.设A∈RL×m是端元光谱库，L为波段数，m为光谱库中的端元数，则稀疏解混模型为

y=A·x+n

(1)

其中，y为L个波段中的单个混合像元的光谱矢量，y∈RL；x是基于光谱库表示的丰度向量，x∈Rm；n为误差项，n∈RL.根据高光谱图像的实际物理意义，丰度向量满足丰度非负性约束(abundance nonnegative constraint, ANC)以及丰度和为1约束(abundance sum-to-one constraint, ASC)，即稀疏解混模型的约束条件为

xi≥0, ∀i

(2)

(3)

其中，xi为x的第i个元素.

由于实际图像中的端元数远小于光谱库的维度，x满足稀疏性.若不考虑式(2)和式(3)的约束，则稀疏解混的优化问题[4]描述为

(4)

(5)

凸优化方法虽然可通过简化式(5)来解决高光谱图像解混问题，但所得丰度矩阵的稀疏度不够高，本研究主要讨论用贪婪算法进行求解.

2 子空间匹配追踪算法

子空间匹配追踪算法是一种经典的联合贪婪算法.考虑到高光谱图像中各端元的相关性，该算法用迭代的方法从光谱库中选择端元来重构高光谱图像，能有效解决丰度非负性的约束问题.算法包括端元选择和丰度估计两部分.规范化的高光谱图像数据和光谱库用于端元提取，原始的高光谱图像数据用于丰度估计.在端元选择模块，SMP算法在光谱库中寻找与残差相关度最高的端元.在相关度足够高的情况下，把信号的索引加入端元集中，再将选择出的端元集与高光谱数据用最小二乘法进行丰度估计.但是，在端元选择模块中，贪婪算法易陷入局部最优，会产生大量冗余端元.本研究将仿生智能优化算法WOA，用于高光谱稀疏解混中，利用WOA搜索精度高及避免局部最优的特点，可有效估计端元集丰度，并在保证误差最小的基础上，能最大程度地去除冗余端元来提高解混精度.

3 WOA及其改进

3.1 WOA

WOA是一种仿生智能算法，具有探测性强、搜索精度高、收敛速度快、不易陷入局部最优等优点，搜索能力优于粒子群优化算法(particles warm optimization, PSO)算法[21]、遗传模拟退火(genetic simulated annealing, GSA)算法[22]和差分进化(differential evolution, DE)算法[23]等.WOA的基本原理如下：

3.1.1 环绕捕食

座头鲸可识别猎物的位置并包围它们.由于当前位置是随机初始化的，在搜索机制建立后，当前位置将会被最优位置代替.此过程表达式为

D=|F·M*(t)-M(t)|

(6)

M(t+1)=M*(t)-B·D

(7)

其中，D为当前位置与最佳搜索代理间的距离；M*为最优位置向量；M为位置向量；t为当前迭代次数；B和F为系数向量，B=2br-bf,F=2r，b是在[0, 2]内随迭代次数增加而线性减小的函数，r是在[0, 1]内的随机向量,f为每个元素都为1的向量.式(6)和式(7)可扩展到n维问题，搜索机制将在超立方体中移动到最佳位置为止.

3.1.2 气泡网攻击机制

气泡网攻击机制的核心是螺旋更新位置.这种方法首先计算座头鲸位置(M,N)和猎物位置(M*,N*)之间的距离.其中，螺旋方程为

M(t+1)=D′·ecl·cos(2πl)+M*(t)

(8)

其中，D′=|M*(t)-M(t)|，为第i头座头鲸和猎物之间的距离；e是定义螺旋线形状的经验常数；l是[-1, 1]内的随机数.

3.1.3 搜索猎物

座头鲸根据其与猎物的位置进行随机搜索.B的变化与座头鲸的搜索方式相关联，所以B>1或B<-1时迫使搜索代理远离当前作为参考的座头鲸，本研究通过随机选择而非选择最佳搜索代理来更新搜索代理的位置.这种机制约束使WOA表现为全局搜索.其数学表达为

D=|F·Mrand-M|

(9)

M(t+1)=Mrand-B·D

(10)

其中，Mrand为随机位置向量.

式(10)表示的鲸群位置更新机制成就了WOA高效的探测能力，它要求鲸群在初始迭代时是互相之间随机移动的.比起PSO和GSA这类单一的搜索机制，WOA在迭代过程中的搜索速度更快.

3.2 改进的WOA

WOA算法仅给出了各个参数的基础设置以及基础的策略选择，仍存在收敛速度慢和收敛精度低的问题.受到回溯搜索算法的启发，本研究提出基于非线性的种群控制参数和进化策略的鲸群优化算法，将原算法中线性变化的种群控制参数替代为正弦函数形式的非线性控制参数，来避免WOA算法陷入局部最优的情况，以期提高全局搜索能力，并通过加入选择策略，引导产生新种群，以更好地控制种群的搜索方向，提高收敛速度.

由B=2br-bf可知，B的取值及变换形式与b息息相关.在WOA中，b是一个在[0, 2]内线性递减的函数，表达式为

b=2-t×2/tmax

(11)

其中，t为当前迭代次数；tmax为最大迭代次数.b控制着算法中的全局探索和局部开发能力，但简单的线性关系并不能充分开发种群的探索能力.因此，本研究引入正切函数来代表非线性关系

b=(bmax-bmin)[1-tan(0.25πt/tmax)]

(12)

其中，bmax和bmin分别为种群控制参数取值范围的最大值和最小值.可见，b仍是[2, 0]内的递减函数.本研究称这种改进方法为基于非线性种群控制参数的鲸群优化算法(improved WOA based on non-linear population control factor, SWOA).

在WOA中，每次迭代完成后，种群仍在产生的最优搜索代理的周围搜索，此行为很容易陷入局部最优，影响整个优化算法的迭代速度和精度.式(7)、(8)及(10)均表示搜索代理以当前最优的搜索代理为标志点进行小范围内搜索或进行弱随机性的搜索.受回溯搜索算法的启发，本研究提出搜索选择方程

M(t+1)=M(t)+G×[M*(t)-M(t)]

(13)

其中，G=3×rand，相当于一个控制种群搜索方向的变量，rand为[0, 1]内的随机数.考虑到WOA的实际算法中，由于用于选择环绕缩小机制或螺旋更新机制的概率p也为随机值，本研究用p代替rand，可有效提高种群搜索和开发能力.这种改进方法称为基于突变策略的鲸群优化算法(improved WOA based on evolution strategy, EWOA)

将上述两种改进方法结合起来，得到基于非线性种群控制参数和突变策略的鲸群优化算法(improved WOA based on non-linear population control factor and evolution strategy, SEWOA)，算法步骤为：

1)初始化鲸群M、b、B和p，并计算每个搜索代理的适应度值.

2)更新p，并按照式(11)更新b和B.

3)若p<0.5，且|B|<1，则当前搜索代理按式(7)、(13)和(14)更新位置.

4)若p<0.5，且|B|≥1，则当前搜索代理按式(12)和式(13)更新位置.

5)对超出搜索边界的搜索代理进行位置修正.

6)更新最佳搜索代理的位置.

7)判断是否符合迭代循环结束的条件.若符合，则输出最佳搜索代理的位置；否则，从迭代开始标志处进行新一轮循环.

3.3 仿真实验与结果分析

通过6种测试函数分别对WOA、SWOA、EWOA 和SEWOA进行验证.测试函数[24]见表1.其中，F1、F2和F3是单模函数[25]；F4、F5和F6是多模函数[26].设种群数目为40，最大迭代次数为1 000，仿真结果如图1.由图1可见，改进后的SWOA、EWOA和SEWOA算法收敛速度更快，收敛精度也更高.对比4种算法分别在6个测试函数中运行20次后所得的收敛精度均值和标准差(请扫描论文末页右下角二维码查看表S1)发现，改进算法在这两个指标上明显优于原WOA.

表1 用于测试改进算法的基准函数

图1 六种测试函数的进化曲线

4 IWOSMP算法

首先，将SMP算法选择的端元集作为候选端元集；其次，采用改进的鲸群优化算法针对此候选端元集进行预解混，通过边界控制解决丰度非负性与和为一的约束问题，得到初步丰度矩阵，在保证重构误差最小的情况下，将丰度较小的端元从SMP得到的端元集中去除来更新端元集；最后，用最小二乘法得到最终的丰度矩阵.

4.1 目标函数与约束条件

采用SEWOA算法进行丰度估计.对式(5)稍作变形得到约束稀疏回归模型，针对每一个像素点求解丰度向量，目标函数构造为

(14)

其中，A为光谱库；Y为实际高光谱图像的观测数据；λ为稀疏性调节参数.为使噪声容限δ尽可能的小，即当δ→0时λ→0，λ取值很小，本研究取λ=2e-3.

采用式(12)使用SEWOA算法求解丰度时，为解决ANC问题，将SEWOA的搜索上限和下限分别设为1和0.为解决ASC问题，在对图像中P个端元解混时，将第P个端元的丰度值设为

(15)

4.2 位置更新机制

由于WOA的搜索代理采用的是随机搜索机制，本研究将鲸群的位置更新数学模型定义为

D=|F·xrand-x|

(16)

x(t+1)=xrand-B·D

(17)

其中，xrand是随机位置向量；x为估计的丰度向量；B为[-1, 1]内的随机值.

座头鲸围绕猎物游动的路径呈现出收缩的螺旋状，假设选择缩小环绕和螺旋更新分别有50%的概率发生，故数学模型为

x(t+1)=

(18)

其中，p是[0, 1]内的随机数.

4.3 IWOSMP算法具体步骤

5 结果与分析

为验证本研究提出的改进鲸群优化的子空间匹配追踪高光谱稀疏解混算法的有效性，分别对两组合成图像(不同SNR以及不同端元数)和真实遥感图像进行端元的提取和解混.将本算法与两种贪婪选择机制类算法SOMP和SMP，3种凸优化算法SUnSAL[27]、SUnSAL-TV[28]和CLSUnSAL[29]进行实验及结果对比.其中，将各算法的参数调至与文献[10-11]和文献[27-29]中相同.合成图像实验中采用均方根误差(root mean squared error, RMSE)[30]来估计丰度误差，则第i个端元的RMSE为

(19)

由于真实遥感图像中无丰度地图，故真实数据与重构图像数据之间的误差表示为

(20)

5.1 合成图像解混实验

5.1.1 实验1

从美国地质勘测局(United States Geological Survey, USGS)提供的矿物光谱库(http://speclab.cr.usgs.gov/spectral-lib.html)所包含的224个波段及498个端元光谱库中选取5个端元，并按照稀疏混合模型产生一幅64×64 像素的合成图像，丰度值满足和为1的约束且在0～0.8随机取值，以此来模拟真实场景不纯在纯像元的情况.在合成图像加入不同程度的高斯白噪声，SNR分别为20、25、30、35、40、45和50 dB.

在进行解混时，IWOSMP算法中WOA的种群数为40，进化代数为1 000，搜索上限为1，搜索下限为0.图2为端元数为5且在不同程度噪声干扰的情况下，不同算法运行20次的后平均RMSE值变化情况.由图2可见，当端元数一致时，即使信噪比不同，IWOSMP算法仍能有良好的解混性能.在低信噪比时，IWOSMP、SMP和SOMP算法的解混结果明显优于SUnSAL、SUnSAL-TV和CLSUnSAL.除此之外，随着信噪比的增加，6种算法的均方根误差呈减小趋势，且IWOSMP算法解混的丰度均方根误差最小.在贪婪算法IWOSMP、SMP和SOMP解混结果中端元集中的端元个数分别为5、7和10，表明IWOSMP算法结果中的端元个数完全正确，而SMP和SOMP算法的结果中存在冗余端元.

图2 不同高斯噪声下5个端元的合成图像的解混结果

5.1.2 实验2

按照稀疏混合模型产生7幅64×64 像素的合成图像.从USGS光谱库中分别随机选取3、5、7、9、11、13和15个端元，丰度值在满足和为1及非负性的前提下，服从狄利克雷分布.在合成图像中加入高斯白噪声使SNR=30 dB.IWOA算法的参数设置同实验1.

图3是30 dB高斯噪声下不同端元个数的解混结果.由图3可见，当端元数较多时，6种解混算法的性能相对较差，但所有贪婪算法(SOMP、SMP和IWOSMP)的解混结果都优于凸优化算法(SUnSAL、SUnSAL-TV和CLSUnSAL)，且IWOSMP算法解混性能最好.图4是不同贪婪算法在30 dB噪声背景下的提取端元数目的结果.由图4可见，IWOSMP算法提取的端元数目最接近高光谱图像中的真实端元数，SOMP和SMP算法中存在大量的冗余端元，说明IWOSMP算法在端元提取方面优于SOMP和SMP算法.IWOSMP算法能有效去除大量的冗余端元，使端元提取的精确度提高，从而改善了解混精度.

图3 30 dB高斯噪声背景下不同端元个数的解混结果

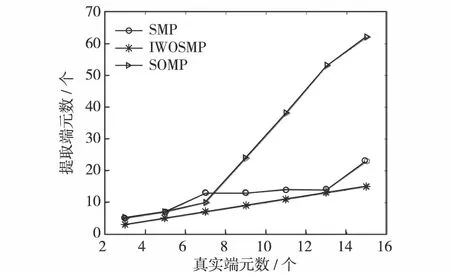
图4 不同贪婪算法在30 dB背景下的端元提取结果

5.2 真实遥感图像解混实验

使用真实数据来验证IWOSMP算法的有效性，但因不存在真实的丰度地图，本研究选取3种地物丰度地图将SMP与IWOSMP算法做视觉对比.此外，由于实际图像中的端元数远小于光谱库的维度，且丰度矩阵具有稀疏性，本研究将丰度矩阵中大于0.001的元素的个数与丰度矩阵所有元素个数的比值定义为稀疏度.

使用AVIRIS Cuprite数据集，选取其中250×191像素的图像，这包括188个波段(已去除低信噪比的波段)，这里所使用的光谱库是USGS光谱库(包含498种矿物)也属去掉低信噪比的波段.

图5 六种算法的3种端元丰度估计图

图5为SUnSAL、SUnSAL-TV、CLSUnSAL、SOMP、SMP和IWOSMP算法得到的真实图像中3个端元的丰度估计图.由图5可见，IWOSMP算法的解混结果比SMP算法更清晰，因此，从定性的角度分析，6种算法都可实现对真实遥感图像的解混，但IWOSMP算法的丰度图相对更清晰.SUnSAL、SUnSAL-TV、CLSUnSAL、SOMP、SMP和IWOSMP的重构误差分别为0.009 3、0.007 7、0.007 5、0.007 4、0.006 5和0.006 4，IWOSMP算法的误差最小.IWOSMP算法是基于SMP算法的改进，因此，本研究还比较了两种算法的稀疏度.其中，IWOSMP算法的稀疏度为0.016 4，SMP算法的稀疏度为0.018 0，前者的稀疏度略低于后者(0.001 6)，表明IWOSMP算法有更好的稀疏性，性能更佳.

结 语

提出基于鲸群优化的子空间匹配追踪(IWOSMP)高光谱稀疏解混算法.先对WOA进行加入非线性控制因子以及进化策略的改进，称为SEWOA算法，再将SWWOA应用到高光谱稀疏解混的SMP算法中，称为IWOSMP算法.该算法利用SEWOA的全局搜索能力和高搜索精度保证了丰度估计的准确性和稳定性.在对SMP算法产生的候选端元集解混过程中，利用SEWOA的边界控制机制所满足的解混过程中的约束条件，及搜索精度高和能够避免陷入局部最优的特点，正确估计端元的丰度系数，在保证重构误差最小的情况下去除系数较小的冗余端元，来提高提取端元的精确度，进而提高解混精度.使用模拟数据和真实数据对比3种凸优化算法(SUnSAL、SUnSAL-TV和CLSUnSAL)和两种贪婪算法(SOMP和SMP)，端元集数目和均方根误差等指标的数据显示，IWOSMP算法精准去除了冗余端元，表现出了更好的端元提取性能，进一步提高了解混精度.对于真实图像数据，IWOSMP算法的丰度估计图像较SMP算法更为清晰，且重构误差较小，稀疏度也相对有所提高.