自卸汽车举升三角臂结构强度有限元及试验分析

苑伍德 罗昆 杨成伦 刘大维

摘要：  为进行自卸汽车举升机构三角臂的结构强度分析，本文以某重型自卸汽车T式举升机构为例，运用多体动力学分析软件Adams，建立举升机构虚拟样机模型，得到举升机构三角臂各铰接点位置的作用力，并应用HyperMesh有限元分析软件，建立以板壳单元为基本单元的三角臂结构有限元模型，分析了最大载荷工况下的结构强度。为验证所建有限元模型的正确性，建立举升结构应变电测试验系统，提取三角臂关键点位的等效应力。研究结果表明，有限元计算结果与试验测试结果相比，关键点位的相对误差为3.42%～15.55%，表明该三角臂有限元模型及分析方法是正确可行的。该研究为举升机构的强度分析和结构的进一步改进提供了参考依据。

关键词：  自卸汽车; 举升机构; 三角臂; 有限元; 应力试验

中图分类号： U469.4; U463.92  文献标识码： A

自卸汽车是通过液压油缸驱动举升机构，将车箱倾斜到一定角度自行卸载货物，靠自身重力使车箱回位的专用汽车。举升机构作为自卸汽车上的重要工作系统之一，其性能的好坏将直接影响自卸汽车的使用性能[1] 。自卸汽车通常在路况比较恶劣的环境下工作，对举升机构中各零部件的强度有很高的要求，因此，对其关键部件举升三角臂进行结构强度分析非常必要。对于举升机构三角臂的结构强度分析，许多学者和企业进行了大量研究，主要采用有限元仿真分析和试验分析两种方法，但将两种方法结合在一起进行分析的研究[2 17] 却非常少。对举升机构三角臂结构强度进行试验分析的正确度高，但在研发过程中结构如需多次改进，则每次都要加工出物理样机在台架上进行试验，耗费大量的人力物力，设计和分析的循环周期较长，成本较高。而有限元仿真分析以其高效和实用性强的特点越来越受开发者的青睐，但由于建模过程中力学模型的简化与实际结构存在差异，导致仿真计算得到的结果与实际相比误差较大。因此，采用有限元仿真与试验相结合的方法可使分析结果更为准确[18] 。基于此，本文采用有限元和试验相结合的方法，对某企业新研制的自卸汽车T式举升机构的三角臂结构强度进行研究，以确保该构件的使用可靠性。该研究为进一步改进自卸汽车的举升结构提供了参考依据。

1 自卸汽车举升机构虚拟样机模型建立

1.1 T式举升机构工作原理

本研究以某重型自卸汽车T式举升机构为例，T式举升机构结构简图如图1所示。T式举升机构主要由三角臂ABC、液压油缸CD和拉杆臂BE组成，点O是车箱与副车架后翻转支座的铰接点。举升机构工作时，高压油液经过液压系统进入液压油缸，油缸活塞杆受油液推力向上伸长，从而驱动三角臂以及拉杆臂顺时针转动举升车箱，举升到一定角度后实现货物的卸载;卸载完成后，液压油缸停止进油，油缸活塞杆开始回缩，依靠自重使车箱复位。

1.2 自卸汽车T式举升机构虚拟样机建模

由于Adams软件中提供的三维实体建模功能较弱，对于举升机构这种复杂的几何模型很难达到理想的建模效果[19 20] 。因此，本文首先在Pro/E软件中建立自卸车的三维实体模型，通过parasiold数据内核，将模型数据转换到动力学分析软件Adams中。为减少在Adams中运动副的数量，防止过约束情况的出现，需要对模型进行简化，将固结在一起的零件，通过布尔运算合并成一个构件，并对举升机构虚拟样机模型添加约束和驱动等，在Adams软件中，建立自卸车举升机构虚拟样机模型。自卸车T式举升机构虚拟样机模型如图2所示。

由图2可以看出，三角臂与车箱前支点对应的铰接点位置用旋转副约束;车箱后支点与副车架对应的铰接点位置用旋转副约束;三角臂与拉杆之间用旋转副约束;三角臂与油缸推杆对应的铰接点位置用旋转副约束;拉杆与副车架对应的铰接点位置用旋转副约束;液压油缸与副车架对应的铰接点位置用旋转副约束;油缸推杆与液压油缸之间用滑移副约束。为举升机构各构件添加质量参数，设置沿坐标轴 Y方向的重力参数，完成自卸车举升机构虚拟样机模型的建立。

1.3 举升机构三角臂作用力仿真分析

仿真计算时，最大举升角为48°，装载量为30 t，举升过程通过液压缸和活塞杆之间移动副的相对运动实现。通过仿真分析计算，三角臂各铰接点作用力随举升时间变化曲线如图3所示。由图3可以看出，三角臂各铰接点的作用力随着举升时间达到最大值后逐渐减小，由于仿真时采用不卸载的方式，各铰接点的作用力无法减小到0。

2 举升机构三角臂的有限元强度分析

2.1 举升机构三角臂的有限元模型建立

通过有限元分析软件HyperMesh，完成三角臂有限元计算模型的网格划分，由于举升机构的三角臂均由板壳单元组成，因此三角臂主要采用边长为4 mm的混合板壳单元（shell）进行划分，与拉杆臂和车箱铰接点的位置采用边长为4 mm的六面体单元（Solid）划分。三角臂中各单元之间主要采用焊接的方式连接在一起，在Hypermesh中，运用焊接单元（Spotweld）进行模拟。举升三角臂的材料为Q345钢，举升三角臂力学参数如表1所示。

整个三角臂的有限元模型由102 397个单元和105 999个节点组成，三角臂有限元模型如图4所示。

2.2 边界条件的确定和载荷的施加

在三角臂有限元模型中，拉杆和车箱约束点确定在铰接点中心节点处，三角臂与拉杆铰接点约束沿x、z方向的平动自由度和沿y、z方向的旋转自由度，三角臂与车箱的铰接点约束x、y、z方向的平动自由度和沿y、z方向的旋转自由度。得到三角臂在举升过程中所受的最大应力，从Adams中求出的力作為载荷，载荷按照三角臂与油缸铰接点处作用力的最大值施加。

2.3 三角臂静态强度有限元计算结果及分析

三角臂受力最大时的应力分布云图如图为5所示。由图5可以看出，应力主要集中在三角臂上边板和下边板处，其中在三角臂的下边板靠近拉杆销孔的焊接处某一位置的应力值较大，应力值最大为228 MPa，小于材料的屈服极限。三角臂局部应力放大图如图6所示。为验证仿真模型及分析方法的正确性，还需要进行应力试验。根据有限元分析结果，选取图5所示的几个点位作为三角臂应变片的粘贴位置。

3 举升机构三角臂结构强度测试试验

3.1 举升机构应变电测试验系统

举升机构应变电测试验系统由数据测量、数据采集和数据处理系统组成，举升机构应变电测试验系统如图7所示。

各测点的应变信号由应变传感器通过武汉英泰斯特电子技术有限公司的16通道动态应变仪采集，并通过LabView软件记录在笔记本电脑中，采集后得到的应变信号采用北京东方振动和噪声技术研究所的Dasp信号分析软件进行处理。

依据有限元分析结果布置应变片位置，由于三角臂结构复杂，主应变方向难以确定，因此布置6个45°电阻应变花，三角臂应变花布置如图8所示。

试验采用的45°电阻应变花，其最大主应力σ1 和最小主应力σ2 分别为

σ1= E 2（1-μ） （εa+εc）+ E 2 （1+μ） （εa-εb） 2+（εb-εc） 2  （1）

σ2= E 2（1-μ） （εa+εc）- E 2 （1+μ） （εa-εb） 2+（εb-εc） 2  （2）

根据第四强度理论，得电阻应变花的等效应力为

σ= （σ1-σ2） 2 2 + （σ2-σ3） 2 2 + （σ3-σ1） 2 2  （3）

而对于平面问题，当σ3 =0时，化简得

σ= E 2  （εa+εc） 2 （1-μ） 2 + 6 （1+μ） 2 [（εa-εb） 2+（εb-εc） 2]  （4）

式中，E為弹性模量;μ为泊松比;εa ，εb 和εc 分别表示0°，45°和90°这3个方向上的应变。

3.2 三角臂应力试验结果与分析

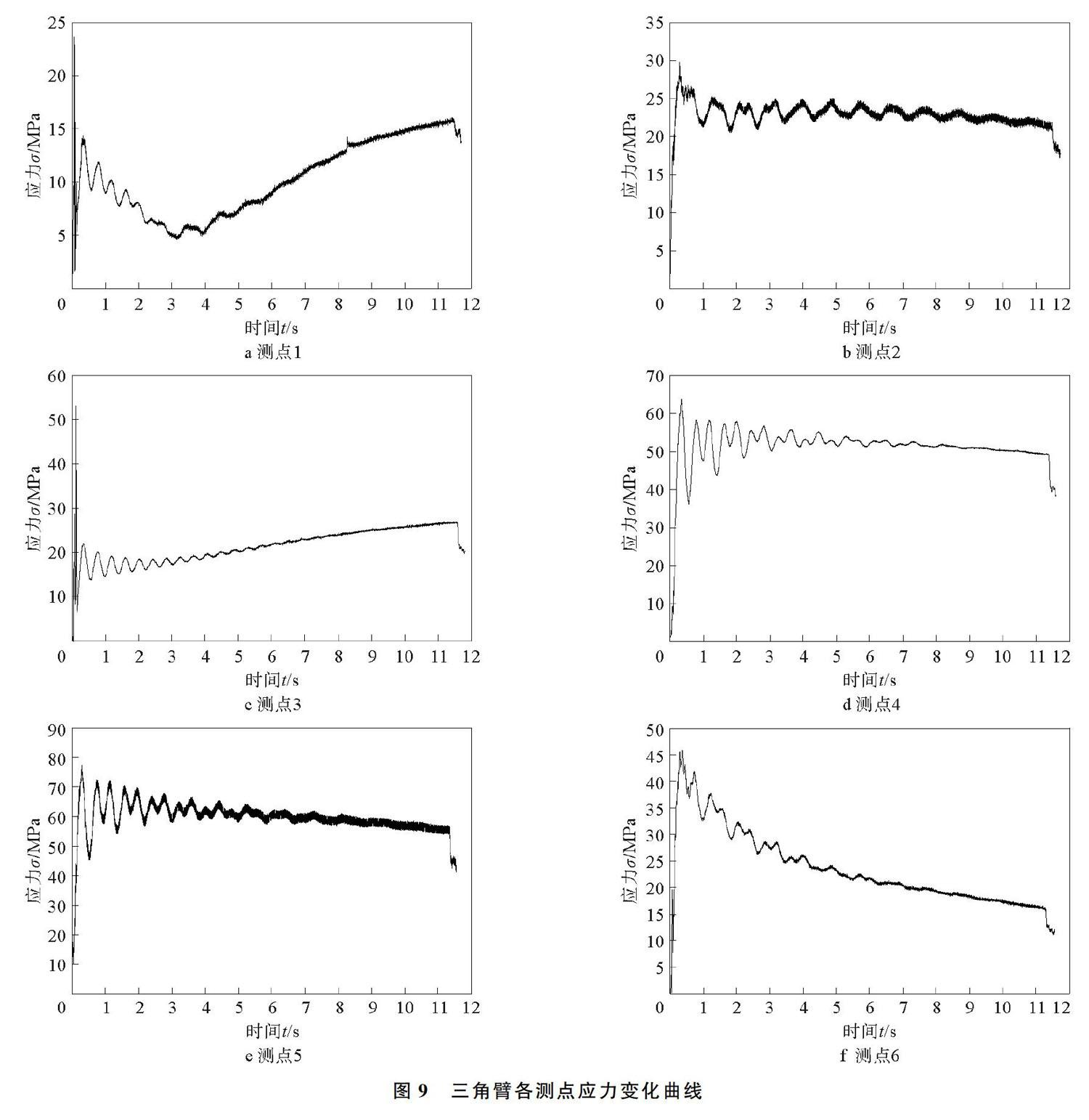
三角臂应力试验在某专用汽车企业液压试验台进行，采用不卸载的方式，举升角为22°，装载量为30 t。 实验获得各测点的应变，根据应力应变分析原理进行分析，三角臂各测点应力变化曲线如图9所示。由图9可以看出，在举升过程中，各测点应力随着举升时间逐渐增加，达到最大值后减小，在0.35 s时，出现应力最大值（举升角度为0.7°）。

3.3 有限元计算结果与试验结果对比

试验获得了自卸汽车举升三角臂各测点的应力最大值和有限元计算得到的应力数值，与有限元计算结果比较如表2所示。由表2可以看出，三角臂各测点的应力有限元计算值和试验值非常接近，相对误差为3.42%～15.55%。说明本研究所建立三角臂结构有限元模型和分析方法是正确的，很好地反映三角实际结构的强度特性，为三角臂结构的进一步改进和优化设计提供依据。

4 结束语

本文以某重型自卸汽车T式举升机构为例，对自卸汽车举升三角臂结构强度有限元模型进行研究。通过建立举升机构虚拟样机模型以及三角臂有限元分析模型，得到三角臂在其最大载荷工况下的应力分布，解决了举升过程中极限应力分布区域难以确定的问题。为验证所建仿真模型的正确性，对三角臂关键点位进行了应力试验，仿真结果与试验结果吻合度很好，表明所建立的仿真模型以及分析方法正确可行。研究结果为举升机构的强度分析和结构的进一步改进提供参考依据。

参考文献：

[1] 葛绪坤. 基于有限元和多体动力学的举升机构疲劳寿命分析[D]. 青岛： 青岛大学， 2014.

[2] 陈德朋. 基于模态参数的白车身有限元模型修正[D]. 长沙： 湖南大学， 2018.

[3] 钱立军， 吴阳年， 黄伟. 重型自卸车举升结构件改进设计及分析[J]. 汽车工程， 2008， 30（1）： 69 71.

[4] 葛绪坤， 樊维， 刘大维. 自卸汽车举升机构应力实验与分析[J]. 青岛大学学报：工程技术版， 2014， 29（1）： 56 59.

[5] 廖芳， 王承. 基于虚拟样机与有限元技术的自卸车举升机构设计[J]. 机械设计与制造， 2005（3）： 90 97.

[6] 尹辉俊， 韦志林， 黄昶春， 等. 自卸车举升三角臂的优化设计[J]. 农业机械学报， 2007， 38（9）： 186 188.

[7] 孙旭. 自卸举升机构的仿真和结构有限元优化[D]. 合肥： 合肥工业大学， 2008.

[8] 张毅， 马力， 李鹏飞. 基于ADAMS的自卸车举升机构优化设计[J]. 专用汽车， 2005（3）： 21 23.

[9] 郑清春， 朱培浩， 薄同伟， 等. 基于Working model自卸汽车举升机构的动力学分析与研究[J]. 现代制造技术与装备， 2008（4）： 70 71， 74.

[10] 周陈霞， 曹芳芳. 基于虚拟样机和有限元技术的举升机构的设计[J]. 机械， 2013， 8（5）： 26 29.

[11] 孙旭. 基于仿真的工程自卸车举升机构有限元优化设计[J]. 工程机械， 2009， 40（7）： 44 48， 7 8.

[12] 栗灿. 基于虚拟样机的自卸车举升机构优化设计研究[D]. 重庆： 重庆交通大学， 2014.

[13] 阚萍， 钱立军， 黄伟. 自卸车举升结构件改进设计及分析[J]. 合肥工业大学学报： 自然科学版， 2008， 31（1）： 143 145， 157.

[14] 王乐宝. 基于虚拟样机和有限元的侧装式垃圾车提升机构优化设计[D]. 青岛： 青岛大学， 2015.

[15] 唐焱， 李发琴， 肖蓬勃， 等. 基于试验设计的自卸车举升机构优化设计[J]. 煤矿机械， 2016， 37（3）： 62 64.

[16] 毛胜辉. 基于最优化理论自卸车液压举升机构优化设计分析[J]. 机床与液压， 2017， 45（10）： 113 118.

[17] 唐云娟， 張斐朗. 矿用自卸车举升机构的优化设计[J]. 装备制造技术， 2019（2）： 123 127.

[18] 刘大维， 刘伟， 孙海霞， 等. 公矿自卸汽车车架模态有限元及试验分析[J]. 矿冶， 2007， 16（4）： 66 68.

[19] 赵强， 孟祥瑞， 于世友， 等. 基于虚拟样机的电动公交车充电弓装置优化设计[J]. 现代制造工程， 2020（3）： 54 59.

[20] 张忠清. 基于虚拟样机的自卸车参数化研究与优化设计[D]. 南京： 南京农业大学， 2011.

Finite Element and Experimental Analysis of Strength of Dump Truck Lifting Triangle Arm

YUAN Wude1 ， LUO Kun1 ， YANG Chenglun2 ， LIU Dawei1

（1. School of Electromechanic Engineering， Qingdao University， Qingdao 266071， China; 2. China National Heavy Duty Truck Group Qingdao Heavy Industry Co， Ltd， Qingdao 266031， China）

Abstract：  In order to analyze the structural strength of the triangular arm of a dump truck lifting mechanism， this paper takes a heavy dump truck T-lifting mechanism as an example and uses the multi-body dynamics analysis software Adams to establish a virtual prototype model of the lifting mechanism to obtain the lift. The force of each hinge point of the triangle arm of the mechanism is applied to the HyperMesh finite element analysis software to establish the finite element model of the triangle arm structure with the plate and shell element as the basic unit， and the structural strength under the maximum load condition is analyzed. In order to verify the correctness of the constructed finite element model， a strain electrical test system of the lifting structure is established， and the equivalent stress of the key points of the triangular arm is extracted. The research results show that the relative error of the key points between the finite element calculation results and the experimental test results is 3.42%～15.55%， which indicates that the established finite element model and analysis method of the triangular arm are correct and feasible. This research provides a reference for the strength analysis and structural improvement of the lifting mechanism.

Key words： dump truck; lifting mechanism; triangle arm; finite element; stress test