基于BP神经网络的冗余机械臂逆运动学分析

刘世平 曹俊峰 孙 涛 胡江波 付 艳 张 帅 李世其

华中科技大学机械科学与工程学院，武汉，430074

0 引言

目前常见的机械臂自由度数大多不超过6，在给定末端位姿的情况下，机械臂各关节的关节角有限制。机械臂各关节角处于奇异形位时，机械臂可能出现无解的情况。冗余机械臂自由度大于末端位姿参数个数时，关节空间中有无数组解与特定末端位姿对应。与非冗余机械臂相比，冗余机械臂能实现避障[1]，具有容错[2]和关节力矩优化[3]等功能，但冗余特性使其逆运动学解法过于繁杂，限制了冗余机械臂的应用。机械臂运动学求解是机械臂位置控制的基础，主要用于机械臂末端执行器的精确定位和轨迹规划，因此研究如何快速获取精确的机械臂逆运动学模型，实现逆运动学求解具有重要的现实意义。

七自由度冗余机械臂逆运动学求解方法主要有几何解法[4]、代数解法[5-6]和迭代解法[7]。几何解法通用性很差，具有一定的局限性且建模求解过程比较复杂，但具有计算较快、精度较高的优势[8]。代数解法在求解过程中涉及到的坐标变换较多，运动学求解精度不高，有一定的误差。迭代解法通过大量数据进行反复迭代，计算量很大，不适用于实时在线任务。SHIMIZU等[9]提出了臂形角的概念，将冗余机械臂的前三个关节、第四个关节、后三个关节分别类比于人体的肩关节、肘关节和腕关节，通过建立臂形角的约束来参数化求解冗余机械臂的逆运动学。OZGOREN等[10]采用解析法完成了冗余机械臂的逆运动学求解并进行了相应的优化，但求解过程复杂，求解精度不高。SINGH等[11]在完成机械臂几何构型分析的基础上，通过旋转角表示并确定肘关节的位置，进而完成其他关节角的运动学求解。LUO等[12]为解决具有关节偏置的机械手运动学求解问题，详细分析了将不同关节角作为冗余参数的情况。为了克服传统方法的不足，遗传算法[13]、神经网络[14]等已用于机械臂逆运动问题的求解。KARLIK等[15]证明了双隐层 BP 神经网络结构在解决机械臂逆运动学问题时具有优势。董云等[16]结合解析法和遗传算法寻找最优关节角，以实现机器人避障及冗余机械手控制。

本文以某型七自由度冗余机械臂为平台，通过建立BP神经网络模型来解决七自由度冗余机械臂逆运动学问题。该方法首先采集10 000组机械臂末端位姿数据及对应的各个关节角度，然后通过训练数据拟合出机械臂逆运动学模型，根据末端位姿反解各关节角度。通过Baxter机械臂在实际运动中获取的数据训练后，BP神经网络进行逆运动学求解得到的结果是有效的单一解，关节角变化是连续光滑的，可以满足运动要求。

1 BP神经网络的搭建

针对Baxter机械臂的逆运动学求解问题，本文建立的BP神经网络模型中，输入层有6个神经元，输入数据包括3个平移和3个旋转的机械臂末端位姿信息；输出层有7个神经元，输出数据为机械臂的关节角度。BP神经网络具体训练步骤如下：

(1)神经网络参数的初始化设置。神经网络的权值和偏置的初始值不能为零，否则会出现权值无法根据输出误差进行有效学习的问题，因此需指定区间(-1，1)，根据一定的概率分布函数，将各个权值和偏置赋予相应的随机值，完成初始化设置。同时对收敛精度ε进行设置，根据预期响应时间，设置最大迭代次数N0，把学习速率α设置为0、1内的小数。

(2)完成数据的正向传播。在神经网络模型中输入数据，经过隐藏层的多次非线性变换，在输出层输出结果。输出层输出数据为

(1)

(2)

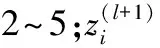
(3)完成整体样本代价函数的计算。根据训练样本的N组输入数据确定整体样本代价函数：

(3)

式中，λ为权重衰减参数；hW,b(*)为激励函数；x(i)为第i个输入数值；y(i)为第i个输出数值；nl为神经网络模型的总层数。

函数计算值趋于稳定后，若其大于收敛精度ε，则结束前向传播，开始误差反向传播，完成进一步的计算；反之则认为模型训练结束，模型参数已准确设置。

(4)完成误差反向传播，得到整体样本代价函数的偏导数，并调整权重大小。其过程如下：

(4)

(5)

按照步骤(1)设置神经网络模型基本参数，依次经过步骤(2) ～ (4)后，模型的权重与偏置都发生变化。重复循环步骤(2) ～ (4)训练模型，直到模型的输出误差小于预设的收敛精度或训练次数超过预设的最大次数。训练次数超过预设的最大次数时，若模型的输出误差仍不收敛，则重新构建并训练新的神经网络模型，得到准确的冗余机械臂逆运动学模型。

2 BP神经网络的优化

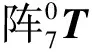
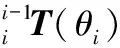
(θ1,θ2,…,θ7)T=T(x,y,z,θx,θy,θz)T

式中，T为7×6的矩阵，其他变量均为数值。

激励函数、隐藏层神经元数量Nn、神经网络层数NL、学习速率α都会对BP神经网络最终的模型拟合精度造成很大的影响，因此本文利用大量的实验数据进行模型的训练，确定合适的模型参数和结构，建立准确、合理、适用的冗余机械臂逆运动学求解模型。

2.1 激励函数的选择

神经网络中，多个线性输入与非线性输出之间的映射关系是通过构建激励函数来实现的。本文引入能够增加非线性因素的激励函数来进行模型的拟合。针对Baxter冗余机械臂的特点，将单极性sigmod函数、双曲正切tanh函数和ReLu(rectified linear unit)函数进行组合，通过分析9种不同神经网络模型的拟合效果来选择适合的激励函数。使用训练集数据，训练神经网络模型并得到其模型参数，使用交叉验证集内的数据检测其模型的输出误差，得到相应的结果。

根据结果可知，将ReLu函数作为激励函数时，输出误差能够稳定收敛并达到最小，说明模型参数在训练过程中不断逼近其真实值，因此将ReLu函数作为神经网络模型中各个神经层的激励函数。

2.2 隐藏层神经元数量

神经元数量Nn与神经网络模型的训练精度及拟合效果呈现正相关的关系，为了提高神经网络模型的训练精度，可增加隐藏层的神经元。然而，神经元的增加会提高神经网络模型的训练难度，从而导致过拟合。为了选择合理的隐藏层神经元数量，本文设置不同的隐藏层神经元数量，模型输出误差

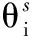
不同隐藏层神经元数量(Nn=10,12,14,16,18,20)模型的输出误差都可以稳定收敛到最小，且输出误差不会随隐藏层神经元的增加而产生太大变化；神经元过多将导致模型变得复杂，训练时间也相应延长。16个神经元模型的收敛最快，其原因在于增加神经元将有效增强神经网络模型的拟合能力，提高模型收敛速度，因此本文选择16个隐藏层神经元的神经网络模型。

2.3 神经网络的层数

理论上，含有至少1个非线性隐藏层和1个线性输出层的BP神经网络能够逼近任何有理函数。增加BP神经网络模型中的隐藏层虽然可以提高拟合精度，但会导致网络结构复杂化和过拟合，进而延长神经网络模型参数的训练周期，降低模型的泛化性。本文分别选择不同层数(NL=3，4，5)的神经网络模型进行实验，并得到其输出误差。不同层数的神经网络模型的输出误差都能够收敛到最小，且输出误差不会随隐藏层的增加而减小，因此，增加神经网络模型的层数并不会明显提高其精度，反而会将模型复杂化。本文最终采用3层神经网络模型来建立Baxter机械臂的冗余机械臂逆运动学求解模型。

2.4 学习速率

神经网络模型的学习速率与神经网络权重变化量的大小成正相关的关系。较大的学习速率导致神经网络权重的变化量很大，使模型收敛不稳定；较小的学习速率导致神经网络权重的变化量很小，使模型收敛时间较长，甚至难以在最大迭代次数之前收敛到最优解。本文分别设置了不同学习速率(α=0.000 1,0.001,0.01,0.1)以求出模型的输出误差。学习速率大于0.001的模型输出误差波动，难以收敛；学习速率不大于0.001的模型能够很好地稳定收敛到最优解，且收敛速度随学习速率的增大而加快。综合考虑系统的收敛速度和稳定性，本文选择学习速率为0.001的神经网络模型。

3 实验设计与验证

为验证上述神经网络模型计算机械臂逆解的有效性与精确度，设计了轨迹跟踪实验来进行数据分析。实验任务要求如下：给定机械臂末端不同的运动轨迹，利用BP神经网络模型反解出各关节角度，控制机械臂按照各关节角运动，机械臂末端的实际运动轨迹与期望轨迹保持一致。设定的机械臂末端运动轨迹包括一个圆心坐标为(0.63 m, 0.38 m,0.05 m)、半径为0.1 m的圆，和一段起始点坐标分别为(0.73 m, 0.38 m, 0.05 m)和(0.73 m, 0.58 m, 0.25 m)的直线。对圆和直线轨迹进行插值，插值点总数为600，记录每个插值点的位姿，将各个插值点的位姿作为BP神经网络模型的输入数据，通过该模型预测出对应各关节角度。

将预测的各关节角度依次发送给机械臂控制器，使其控制机械臂各关节运动，运动轨迹如图1所示，图中圆点为机械臂实际运动轨迹，曲线为期望运动轨迹。由图1可以看出，实际运动轨迹与期望运动轨迹几乎重合。经过计算，机械臂末端运动轨迹为圆时，拟合误差(实际运动轨迹与期望运动轨迹的误差)为9.8 mm；机械臂末端运动轨迹为直线时，拟合误差为1.6 mm。在实际任务中，该误差是可以接受的，能满足我们的运动要求。这表明通过建立BP神经网络来拟合机械臂逆运动学模型的方法是可行的，并且求解精度较高，可以满足实际需求。

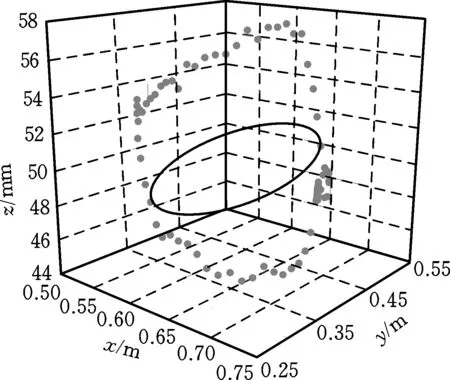
(a) 圆轨迹

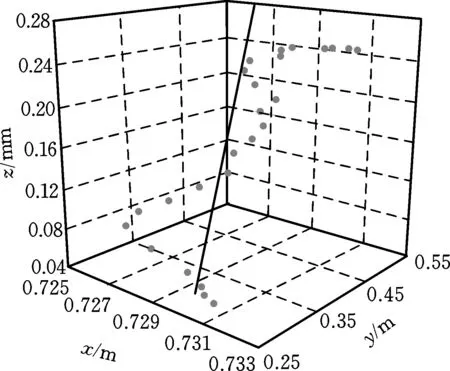
(b) 直线轨迹

4 结论

本文针对Baxter七自由度机械臂，通过搭建BP神经网络模型来实现冗余机械臂逆运动学的求解，建立了冗余机械臂工作空间到关节空间的映射关系，选择了适合的神经网络模型激励函数、隐藏层神经元数量、神经网络层数、学习速率。轨迹跟踪实验表明，利用BP神经网络来拟合机械臂逆运动学模型的方法是可行的。