一种滚动密封式爬壁机器人动力学建模与分析
秦基伟 常 勇 袁兵兵 付兴伟 王天龙
1.中国科学院沈阳自动化研究所机器人学国家重点实验室,沈阳,110016 2.中国科学院机器人与智能制造创新研究院,沈阳,110016 3.中国科学院大学沈阳自动化研究所,沈阳,110016 4.中国长江三峡集团有限公司,北京,100038
0 引言
水电站混凝土流道壁面因长期受水流冲击和日晒雨淋会产生麻面、裂缝、凹坑等缺陷,需要进行定期检查维护。传统的人工搭建脚手架检修平台登台检测的方式费时费力,危险性高。一些学者提出利用爬壁机器人搭载检测仪器进行检测。对于混凝土壁面,爬壁机器人一般采用负压吸附方式附着于壁面,利用足式、轮式或履带式行走机构实现沿壁面的运动[1-3]。
负压吸附式爬壁机器人需要设计密封装置维持腔内负压,目前的密封装置根据密封机理一般可分为滑动密封和滚动密封。滑动密封是指爬壁机器人运动时密封装置与壁面之间的摩擦力以滑动摩擦力为主。为减小密封装置与壁面之间的摩擦力,并适应凹凸不平的壁面,文献[4-9]设计的滑动密封装置采用摩擦因数较小的柔性材料,但由于密封装置与壁面之间存在较大的作用力,故机器人运动时存在摩擦阻力大、密封材料耐磨性差、对壁面凸起适应性差的缺点。
针对滑动密封方式存在的问题,有学者开展了基于滚动密封机理的爬壁机器人研究。滚动密封采用移动装置与密封装置的一体化设计,密封单元在滚动的同时维持密封效果,减小了运动时的摩擦阻力和密封材料的磨损。目前的滚动密封主要有两种形式:纽约城市大学研制的Rise-Rover[10]采用带有吸盘的履带,履带在运动的同时能够吸附在壁面,机器人运动阻力小,能够适应带有一定程度裂痕和沟槽的壁面,由于负压腔的有效吸附面积较小,机器人负载自重比较小,然而由于履带结构特殊,故导致制造难度较大;美国ICM公司设计了一种滚动密封式爬壁机器人[11],该机器人利用履带在运动的同时对负压腔进行密封,具有负载大、对壁面适应性强等特点,但是其质量和功耗较大。
目前针对履带式爬壁机器人的动力学分析主要以磁吸附式爬壁机器人为研究对象[12-15],缺少对负压吸附履带式爬壁机器人的动力学分析,且较少有论文针对机器人转向时的滑移距离进行求解。本文根据文献[11]的研究工作,结合混凝土壁面缺陷检测的实际任务需求,介绍了一种基于滚动密封机理的爬壁机器人机构,分析了其运动与密封机理,以履带的摩擦力和牵引力为求解对象建立了机器人直线及转向运动的动力学模型,开展了仿真分析和样机实验研究。
1 爬壁机器人机构设计
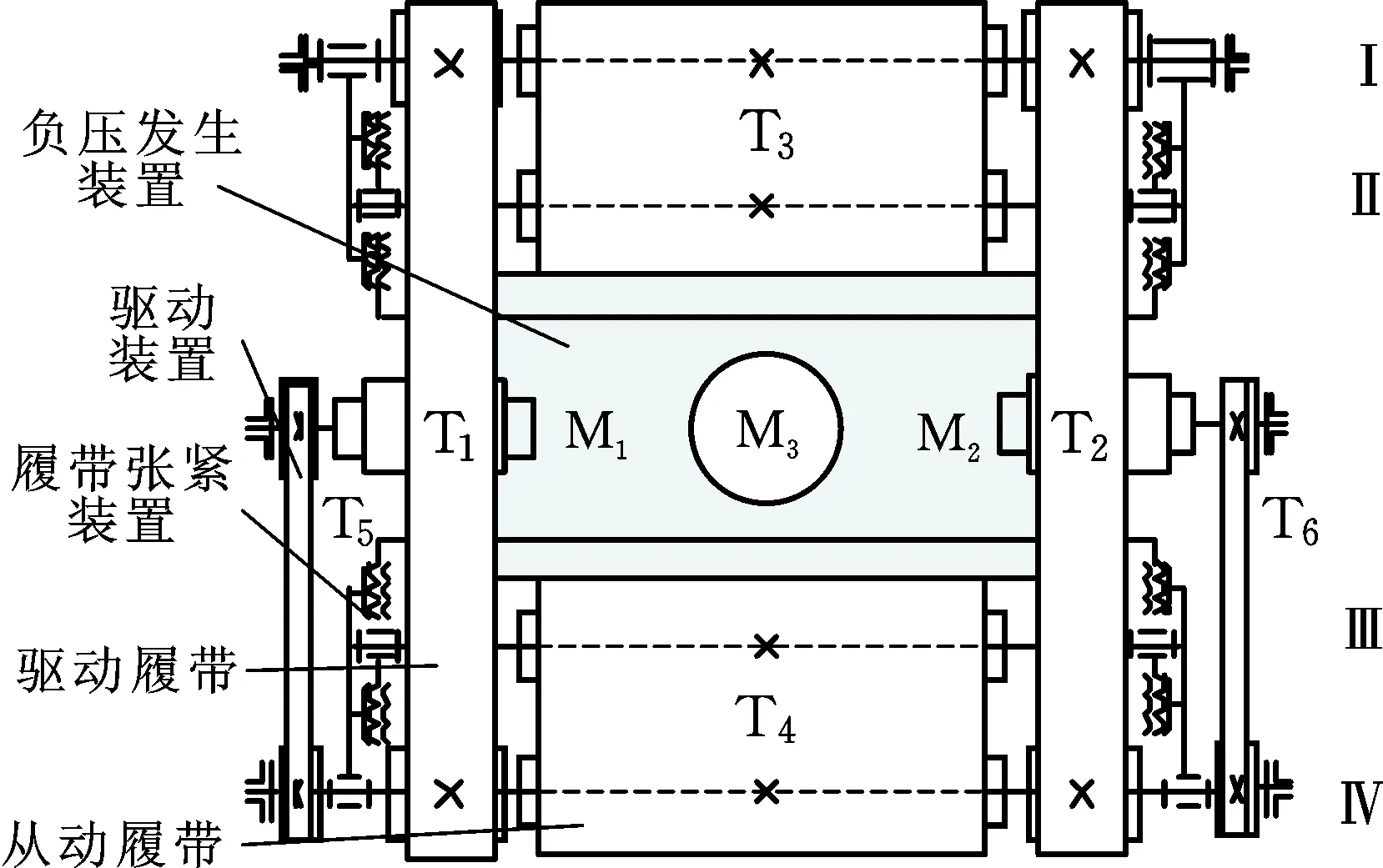
图1 爬壁机器人机构简图Fig.1 Schematic diagram of the wall-climbing robot mechanism
爬壁机器人的机构简图见图1,该机器人主要由负压发生装置、驱动装置、履带张紧装置、驱动履带(T1、T2)和从动履带(T3、T4)组成,其中驱动装置分别由电机M1与同步带T5以及电机M2与同步带T6组成。该机器人具有直线运动、原地转向和沿任意半径转向3种运动模式。由驱动电机M1、M2分别经同步带T5、T6将运动和动力传递至驱动履带T1及T2,当T1与T2移动速度等值同向时可实现直线运动,二者速度等值反向时可实现原地转向,二者速度大小或方向不同时可实现任意半径转向。
机器人的吸附及滚动密封原理如图2所示,通过风机叶轮(M3)的高速旋转抽出腔内空气,履带T1~T4分布在负压腔四周,在运动的同时维持对腔体的密封。负压腔左右侧面黏结泡棉块并与驱动履带贴合,负压腔前后的密封弧板与从动履带外轮廓弧面贴合,从而实现对负压腔的密封,以维持腔内负压值,使机器人吸附在壁面上。

(a) 主剖视图

(b) 左剖视图
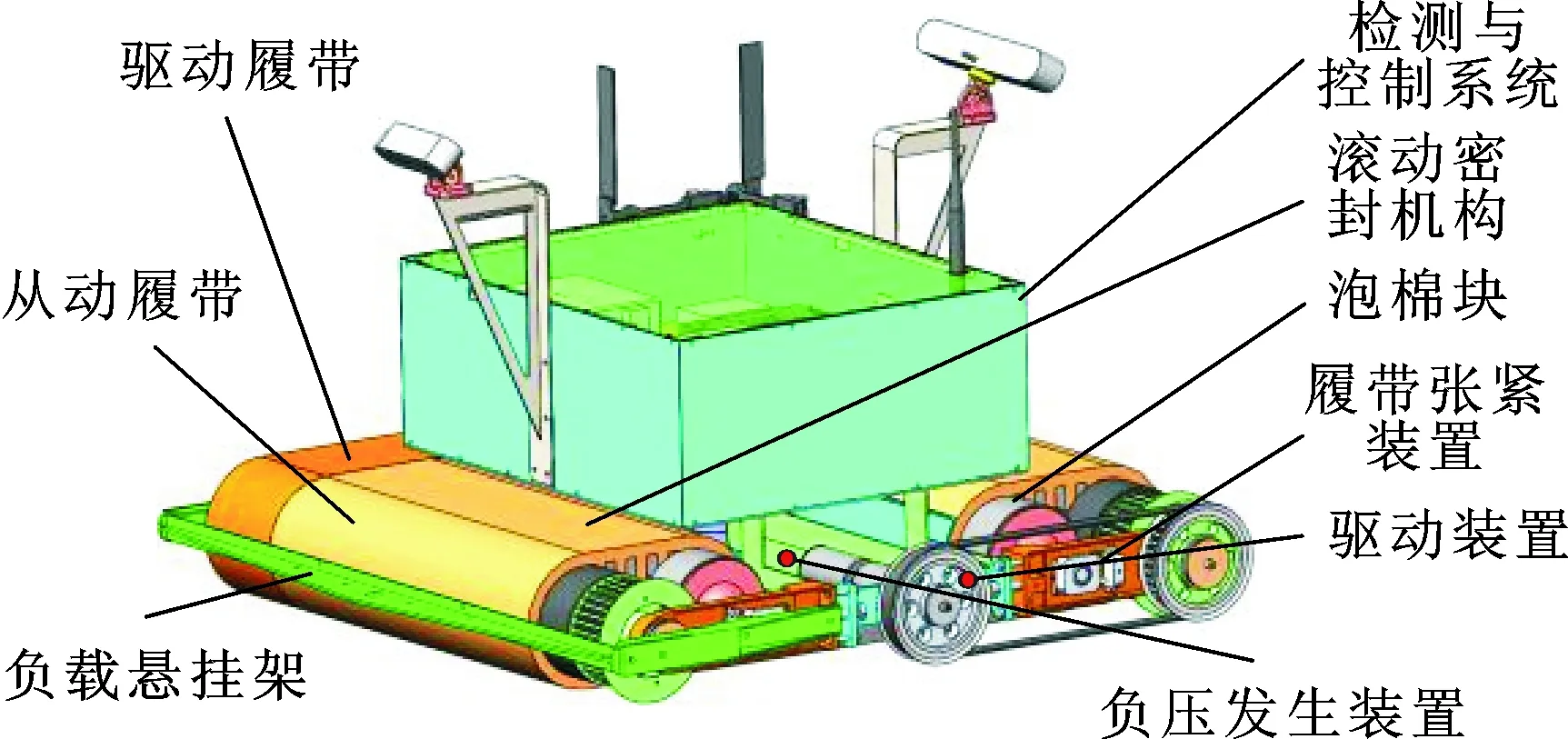
图3 爬壁机器人结构图Fig.3 Structure of the wall-climbing robot
爬壁机器人由负压发生装置、驱动装置、滚动密封机构、履带张紧装置、负载悬挂架、检测与控制系统组成,如图3所示。滚动密封机构由4根轴(图1中Ⅰ~Ⅳ)支撑分布在负压腔四周的4条履带。驱动履带由同步带及其外层黏附的泡棉组成,同步带用于传动,泡棉的一侧端面和内表面分别与从动履带端面和泡棉块底面贴合,以实现对负压腔左右的密封;从动履带外轮廓与密封弧板贴合实现对负压腔前后的密封,从动履带及其支撑筒均采用泡棉材料,能够降低履带的径向刚度,提高履带对壁面的适应性。履带张紧装置用于连接轴Ⅰ、Ⅱ以及轴Ⅲ、Ⅳ,并利用螺旋传动机构调整轴间距,张紧履带,以保证从动履带与弧面贴合。由于机器人与壁面之间以泡棉接触,故对不平整壁面的适应性较强。
2 爬壁机器人动力学建模
爬壁机器人动力学建模用于计算机器人的驱动力矩与其结构参数、姿态角、吸附力之间的关系,为机器人的机构优化、电机选型与运动控制提供理论依据。本节建立了机器人直线运动及转向动力学模型,由于机器人带缆作业,故模型中考虑了电缆质量。为便于动力学建模,假设:①限定工作平面为竖直壁面;②规定机器人运动方向为纵向,垂直于运动方向为横向,机器人在几何上关于纵向和横向平面对称,其质心和几何中心在壁面上的投影重合;③单条履带的接壁段压力均匀分布;④履带在其运动方向上不打滑。
2.1 直线运动动力学模型
爬壁机器人沿壁面向上做直线运动时,通过两侧履带的运动产生牵引力,牵引力克服运动过程中的重力、摩擦阻力,驱动机器人运动。平行于壁面方向,进行机器人的受力分析,如图4所示,定义PxPyP为本体坐标系,原点P固定在机器人质心,xP为机器人运动方向,yP垂直于机器人运动方向。
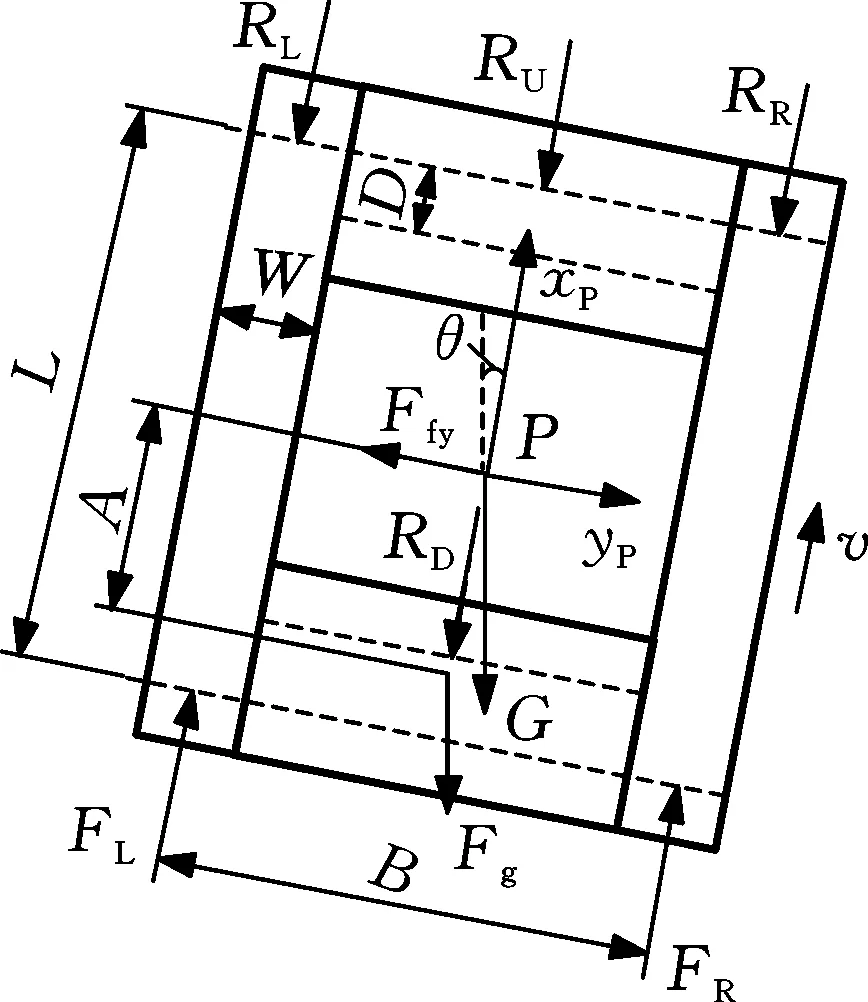
图4 爬壁机器人直线运动受力模型Fig.4 Force model for linear motion of wall-climbing robot
建立机器人直线运动的动力学方程:
(1)
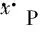
假设机器人在横向上不发生滑移,解式(1)得
(2)
式(2)说明牵引力与机器人和电缆的重力、摩擦阻力以及机器人姿态角有关。履带在直线运动过程中,摩擦阻力的大小与履带接壁段压力及其自身形变量有关[16],以下分别求解各条履带的接壁段压力及压缩变形。垂直于壁面建立平衡方程为
(3)
式中,Fp为总吸附力;FNL、FNR、FNU、FND分别为壁面对驱动履带T1、T2及从动履带T3、T4的支持力;kf为驱动履带的接壁段压力占总支持力的比值;L为驱动履带接壁段长度;D为从动履带接壁段长度;h1为爬壁机器人本体的重心高度;h2为电缆插头距壁面的高度。
履带滚动时受壁面压力而产生压缩,由于履带材料的黏弹性,弹性变形在接触消除后才能恢复,造成接触边的压力大于消除接触边的压力[17],因此履带压力会出现在相对履带接壁段中间靠前的位置。图5所示为考虑压缩变形,单条履带匀速运动时的受力分析。建立平衡方程:
(4)
式中,F′p为传递到履带两轮轴的吸附力,假设均匀施加于两根轮轴上;L′为两轮轴中心距;FN为履带受壁面的支持力,作用点距履带接壁段最前端L′/2;Ft为履带牵引力;Rr为摩擦阻力;e为履带压缩后使履带接壁段向前延伸的长度;r为履带的外轮廓半径。
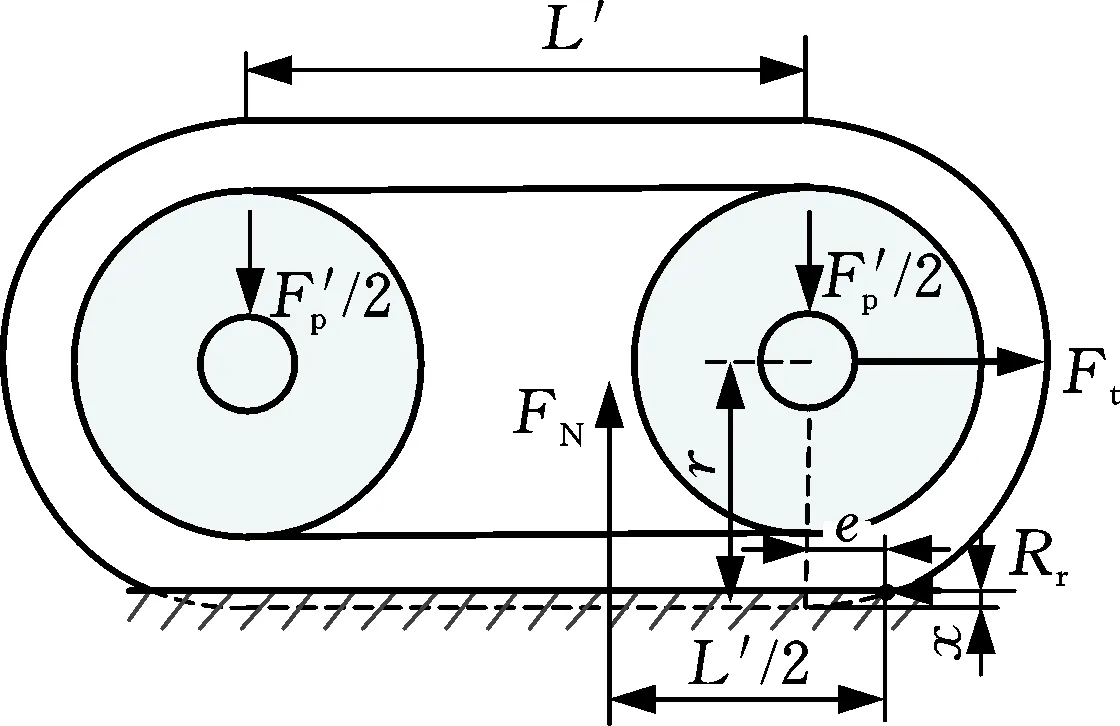
图5 单条履带运动时的受力分析Fig.5 Force analysis of single track movement
履带受壁面支持力产生的压缩量
(5)
式中,t为履带外层泡棉厚度;E为泡棉弹性模量;Ai为履带接壁段面积。
由式(4)、式(5)得履带运动时的摩擦阻力
(6)
由式(3)、式(6)得各条履带的摩擦阻力:
(7)
式中,AD、AS分别为单条驱动履带和单条从动履带的接壁段面积。
由式(7)得摩擦阻力主要与吸附力、机器人姿态角、履带的弹性模量及其尺寸有关。将式(7)代入式(2)即可得到直线运动时履带牵引力的求解公式。结合式(3)、式(7)得,减小从动履带的径向刚度可以将壁面对履带的支持力更多地分配给驱动履带,提高履带的驱动力,但是在同等吸附力下,较软的履带由于压缩量较大,会增加运动阻力。
2.2 转向动力学模型
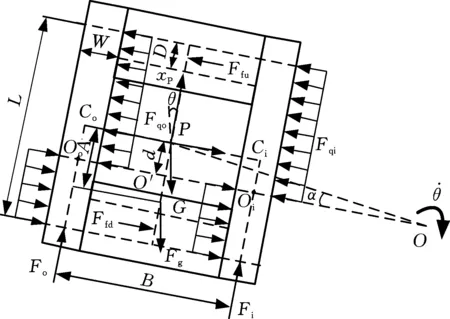
图6 爬壁机器人转向受力分析模型Fig.6 Steering force analysis model for wall-climbing robot
爬壁机器人在壁面转向过程中,通过两侧履带的速度差产生转向力矩,并克服由重力、离心力、摩擦力产生的转向阻力矩实现转向。机器人转向受力分析模型如图6所示,由力的平衡条件可知,机器人以较低速匀速转向时,y轴方向的合力与离心力平衡。为平衡重力和离心力在y轴方向的分量Gy及Fny,机器人两侧履带的瞬时转向中心不再处于履带接壁段质心,而会沿x轴方向偏移。机器人转向动力学采用瞬心模型,即将机器人在某一时刻的运动看作是绕瞬心的旋转。图6中O为机器人旋转中心,定义O在机器人纵轴方向的投影为O′,O′到P的距离为d,OO′与OP之间的夹角为侧滑角α。机器人在转向过程中,离心力作用于P点,沿OP方向,大小为
Fn=mω2R
(8)
式中,ω为爬壁机器人转向角速度;R为旋转中心到机器人质心的距离。
为分析履带受到的摩擦力,取履带接壁段微元面积为dxdy,微元所受摩擦力为df,df与微元的速度方向相反,将df沿x轴和y轴方向分解,如图7所示。
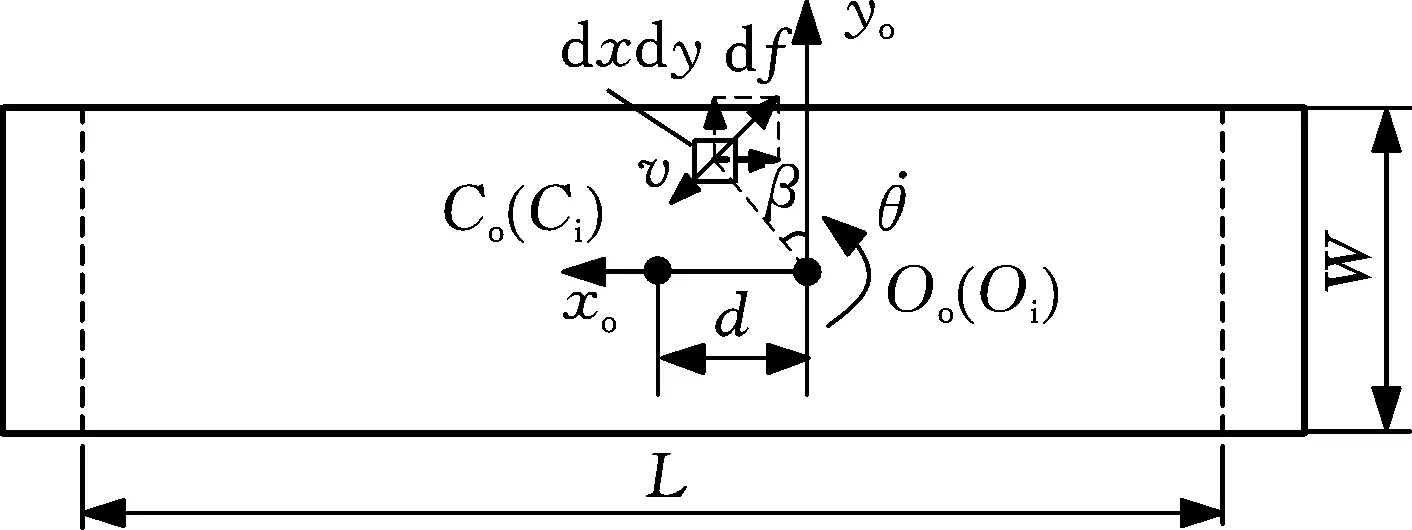
图7 履带接壁段微元所受摩擦力Fig.7 Friction on the tracked wall segment element
将df在xo方向的分量在履带接壁段面积上积分,得壁面对驱动履带的纵向摩擦力
(9)
式中,W为履带宽度;S为履带接壁段面积。
式(9)的积分公式是关于变量y的奇函数,且积分面关于x轴对称,故Ffx=0。将横向摩擦力简化为均布载荷,如图8所示。

图8 履带摩擦力分布简化模型Fig.8 A simplified model of the tracked friction
设内外驱动履带单位长度的横向摩擦阻力为Fqi、Fqo:
(10)
式中,μ1为驱动履带与壁面之间的摩擦因数;FNi、FNo分别为内外侧驱动履带单位长度的法向支持力。
由式(3)、式(10)得壁面对驱动履带的横向摩擦力
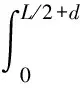
(11)
Ffy相对于瞬心的转向阻力矩

(12)
从动履带T3、T4受到的横向摩擦力分别为
(13)
式中,μ2为从动履带与壁面之间的摩擦因数。
FU、FD相对于瞬心的阻力矩
Mμ2=FU[(L-D)/2+d]+FD[(L-D)/2-d]
(14)
重力与离心力的合力相对于瞬心的阻力矩
Mn=(Fncosα-Gsinθ)d+Fg(A-d)sinθ
(15)
总的转向阻力矩为式(12)、式(14)、式(15)之和,即
Mr=Mμ1+Mμ2+Mn
(16)
机器人转向时的驱动力矩
Md=(Fo-Fi)B/2
(17)
式中,Fi、Fo分别为内外驱动履带牵引力。
机器人的转向动力学方程为
(18)
式中,IO′为机器人相对于O′的转动惯量。
机器人在横向上受力平衡,即
(19)
由于侧滑角α较小,sinα≈0,由式(3)、式(8)、式(11)、式(13)、式(18)、式(19)得滑移距离
(20)
联立式(16)~式(18)得驱动履带的牵引力:
(21)
由式(2)、式(7)、式(21)知,机器人在直线运动及转向时,驱动履带的牵引力主要与机器人的重力、吸附力、外形尺寸、姿态角及履带与壁面之间的滑动摩擦因数有关。进行机器人的轻量化设计、提供合理的负压值、适当减小机器人的长宽比、减小被动履带与壁面的滑动摩擦因数都有利于减小机器人运动时的牵引力。
3 仿真分析与样机实验
3.1 仿真算例1
机器人的相关参数如表1所示,给定负压值为7 kPa,负载为10 kg,分析了机器人直线运动及转向时两侧驱动履带牵引力随姿态角的变化。
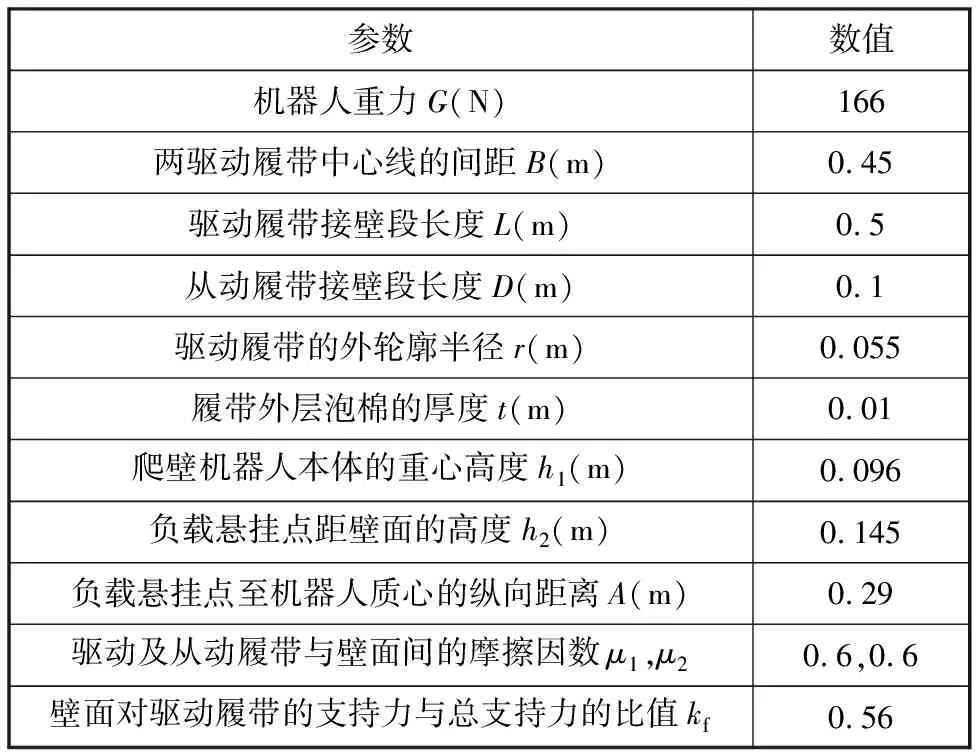
表1 爬壁机器人相关参数
匀速直线运动时的仿真结果如图9所示,θ∈(-270°,-90°)时机器人向下运动,θ∈(-90°,90°)时机器人向上运动;图中各标记点坐标:a(-204°, -128 N),b(-180°, -115 N),c(-155°, -128 N),d(-24°, 163 N),e(0°,150 N),f(24°,163 N)。由图9可知:①由于在不同姿态角下,机器人的重力沿运动方向的分量及履带支持力的分布不同,导致驱动履带的牵引力随姿态角发生变化;②机器人竖直向上运动时,两侧驱动履带牵引力之和达到最大值,且与机器人运动方向相同;③竖直向下运动时,履带牵引力与机器人运动方向相反,以平衡重力;④机器人向下运动时的牵引力大于相同姿态向上运动的牵引力,因为向下运动时,重力沿机器人运动方向的分量变为运动的动力。
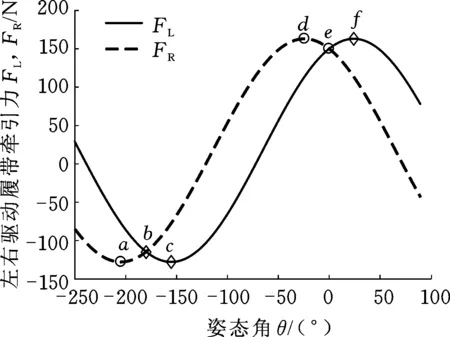
图9 直线运动时驱动履带牵引力随姿态角的变化Fig.9 The change of the driving crawler traction with altitude angle during linear motion
机器人以线速度8 m/min、转弯半径1 m做顺时针匀速转向,转向时内外侧驱动履带牵引力随姿态角的变化如图10所示。由图10可知:①转向过程中,多数姿态角下两侧驱动履带的牵引力存在一定差值,主要利用差值形成的驱动力矩实现转向;②两侧驱动履带牵引力随姿态角波动较大,主要是由于随着姿态角的变化,机器人的重力沿运动方向的分量随之变化,内外侧履带牵引力的大小分别在机器人姿态角为-208°和8°时最大。
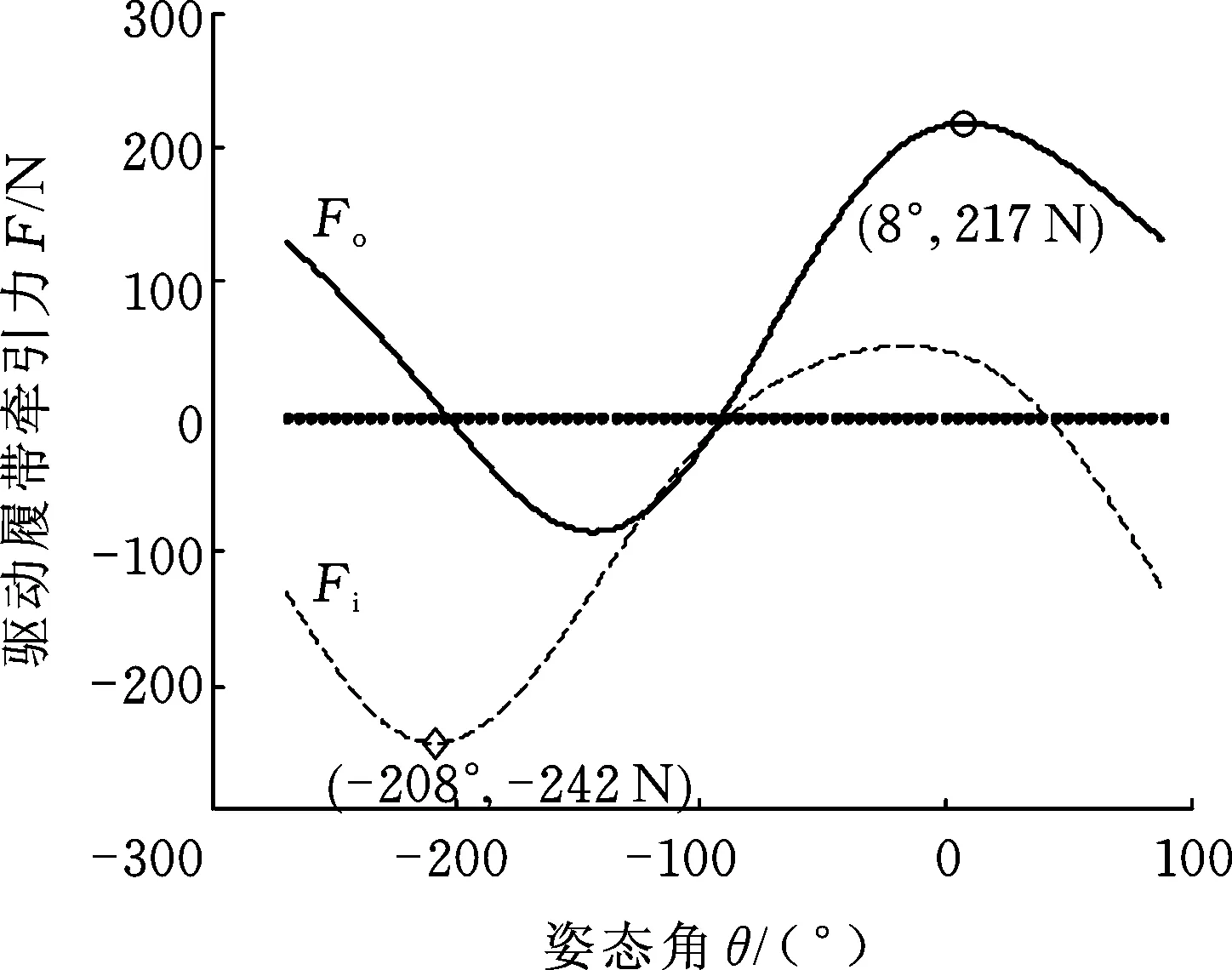
图10 转向时驱动履带牵引力随姿态角的变化Fig.10 The change of the driving crawler traction with altitude angle during steering
3.2 仿真算例2
分别计算出相同质量下,采用滑动密封和滚动密封方式的爬壁机器人在运动过程中的摩擦阻力并进行了对比。假定壁面环境为平整的混凝土壁面,对于滑动密封式爬壁机器人运动时的摩擦阻力,其力学模型和相关计算参数参照文献[5],滚动密封式爬壁机器人运动时的摩擦阻力计算方法参照式(7)。
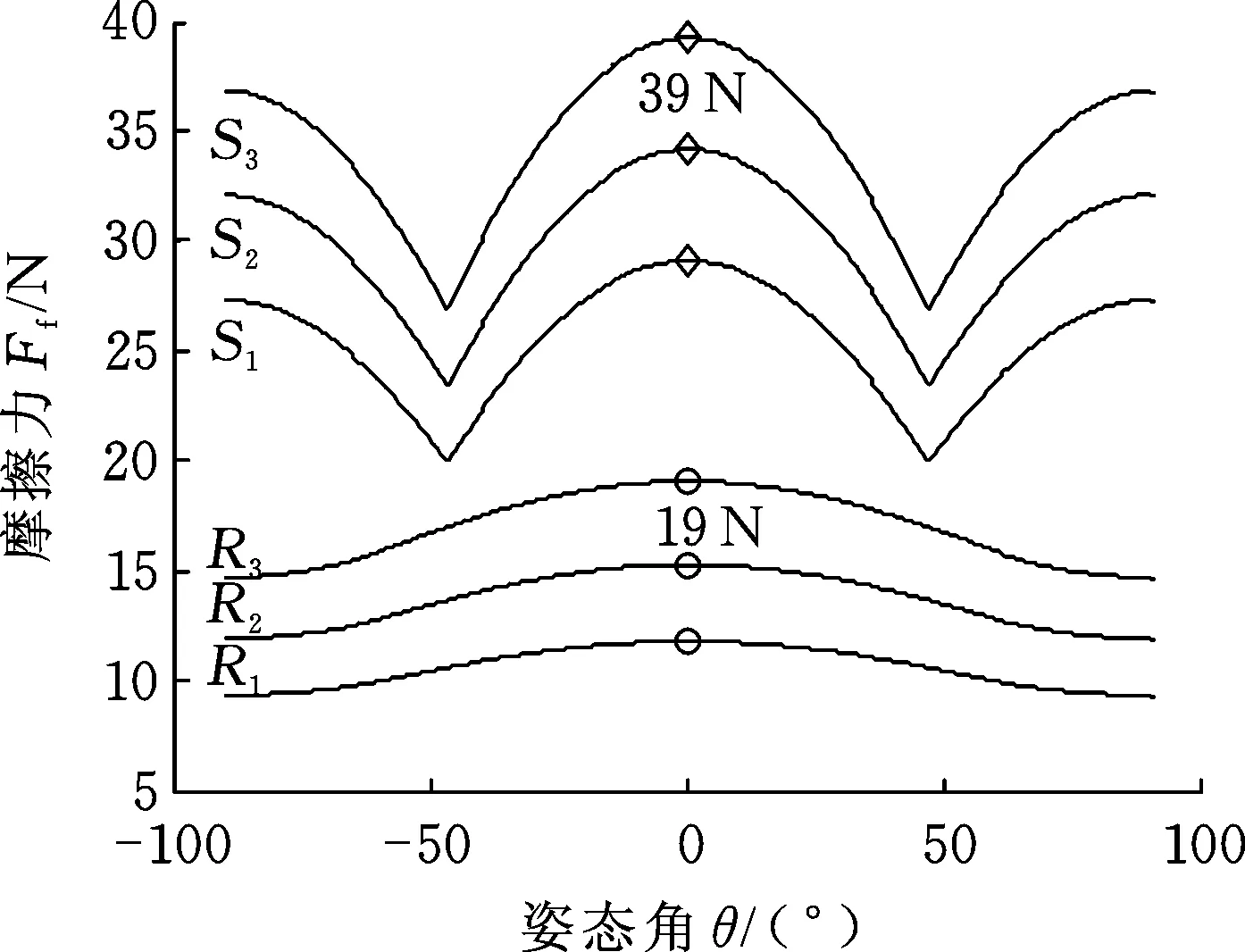
图11 滚动密封式与滑动密封式爬壁机器人摩擦阻力对比Fig.11 Comparison of frictional resistance between rolling seal and sliding seal type wall-climbing robot
比较相同负载下爬壁机器人直线运动时的摩擦阻力,如图11所示,图中,S1、S2、S3分别为滑动密封式爬壁机器人负载为6 kg、10 kg、14 kg时的摩擦阻力;R1、R2、R3为滚动密封式爬壁机器人对应负载时的摩擦阻力。由图11可知:①摩擦阻力的大小随机器人运动时的姿态角发生变化,且在竖直姿态达到最大值;②相同负载下,与滑动密封式爬壁机器人相比,滚动密封式爬壁机器人的摩擦阻力及其波动幅度较小。
3.3 样机实验
开展了爬壁机器人Ⅰ型样机的研制与实验研究,机器人总质量为17 kg,整体尺寸为650 mm×610 mm×400 mm。进行了机器人在不同类型壁面上的实验,如图12所示,图12a、图12b中机器人携带有检测仪器,图12c、图12d中携带有10 kg负载。各类壁面的特性及机器人在壁面的运动情况如表2所示。

(a) 常规壁面实验

(b) 光滑壁面实验

(c) 粗糙壁面带负载实验

(d) 带负载跨越凹槽实验
牵引力与电机功率之间的关系为
Ft=ηPm/v
(22)
式中,η为传动效率,η=0.72;Pm为电机功率;v为机器人速度。
根据机器人带负载在常规壁面运动的实验参数,由式(22)计算出机器人在3种运动状态下履带的牵引力,如表3所示。机器人的实际牵引力与图9、图10对应运动状态下的牵引力相比,误差小于7%。
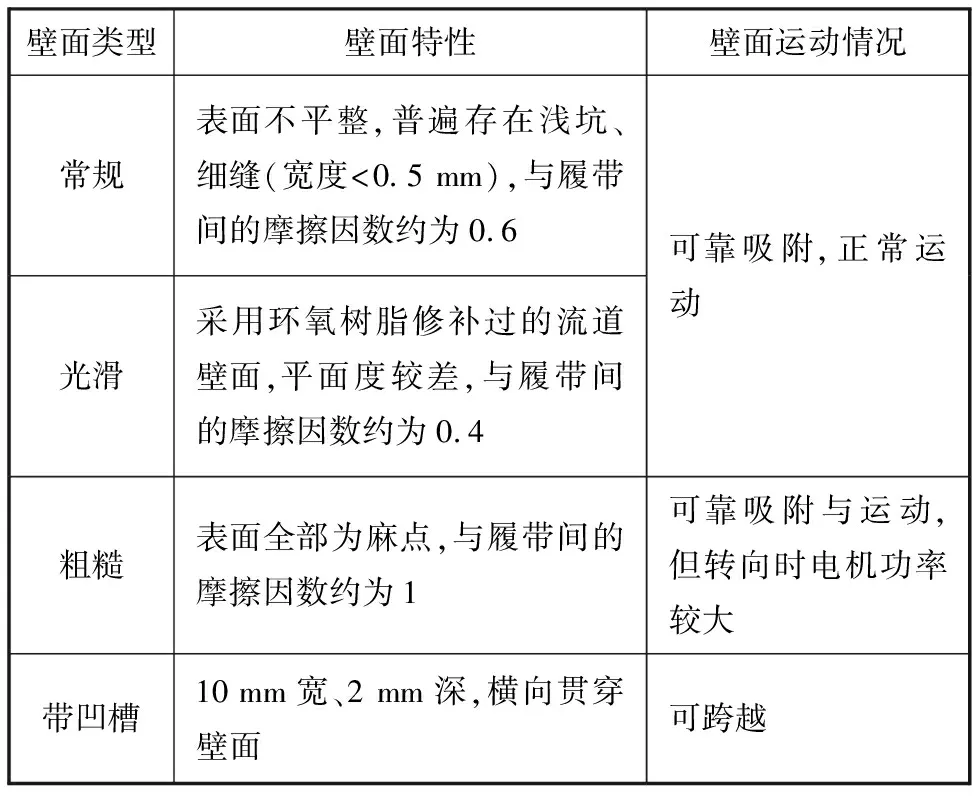
表2 机器人在各类壁面的适应性
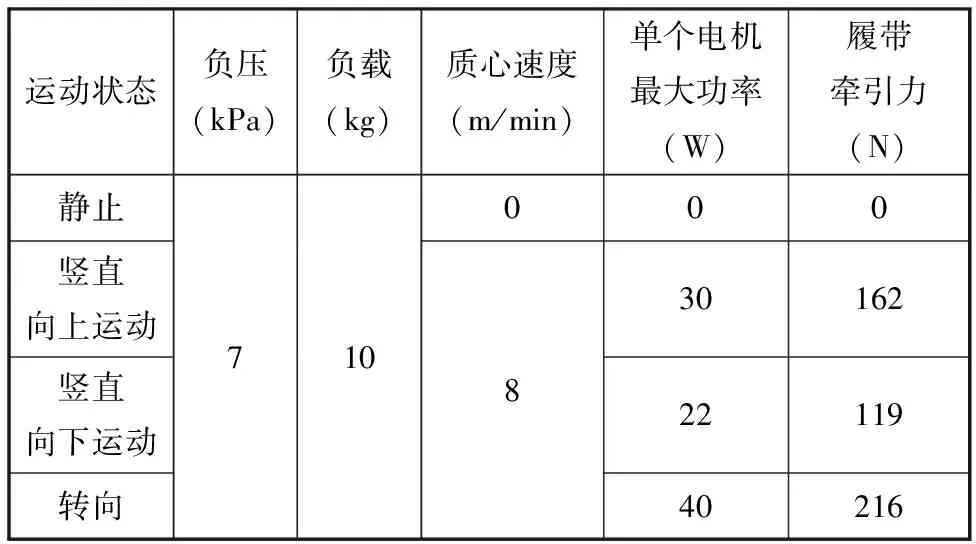
表3 爬壁机器人实验参数
根据实验结果得出以下结论:
(1)机器人对壁面适应性较强,能够在常规、光滑或粗糙的混凝土壁面灵活运动,可适应带有浅坑、脱皮及表面不平整的壁面,能够跨越小型凹槽。
(2)机器人的密封可靠性较高,能够连续运行较长时间。
(3)通过带负载实验证明了机器人有效负载较大。
(4)机器人的负载能力与吸附装置的负压值、壁面粗糙度及电机扭矩有关。通常在电机扭矩足够及密封良好的条件下,增大负压值可提高机器人的负载;在负压相同且电机扭矩足够的条件下,机器人在粗糙壁面上的负载较大,但是在粗糙壁面上转向时损耗的电机扭矩也较大,此时负载主要受限于电机扭矩。
4 结论
(1)介绍了一种滚动密封式爬壁机器人,分析了其密封与运动机理。
(2)提出了一种多履带协调运动的爬壁机器人动力学建模方法,推导出该机器人直线运动及转向动力学方程,得出这两种运动状态下履带牵引力与机器人姿态角、重力、吸附力之间的关系。
(3)分析了直线运动及转向时,履带牵引力与机器人姿态角之间的关系。机器人处于竖直向上姿态时,直线运动所需的总牵引力最大;转向过程中两侧履带牵引力差值较大,利用差值形成的驱动力矩实现转向。
(4)由爬壁机器人动力学模型可知,与滑动密封式爬壁机器人相比,滚动密封式爬壁机器人在直线运动时的摩擦阻力较小。
(5)样机实验验证了研制的爬壁机器人具有摩擦阻力小、负载大、对壁面适应性强的优点。

