顾及形变的影像边缘ICP匹配技术

高 力，金 飞，江振治，王 番，芮 杰

(1. 信息工程大学，河南 郑州 450052； 2. 西安测绘研究所，陕西 西安 710054； 3. 地理信息工程国家重点实验室，陕西 西安 710054)

影像匹配技术的实质是评估影像间特征的相似性。目前，影像的点特征匹配是主流技术，如模板匹配[1]、多维度特征描述(SIFT、SURF)等。点特征具有精度高、速度快、几何变形不敏感的优点[2]，但点之间连接关系弱，缺乏整体约束，容易受到噪声、遮挡等因素的干扰。

影像的边缘是影像不同区域间的分界线，是影像的显著、整体性特征。直线是线特征的一部分，文献[3]从直线特征描述的角度提高匹配质量；文献[4]用平差原理约束短小直线的匹配；文献[5]优化直线提取精度提高匹配质量；文献[6]使用几何约束提高直线匹配精度；文献[7]利用点与直线进行综合匹配。直线特征形式简单，但信息不足，需要辅以其他手段组合、约束才能完成匹配。

曲线特征信息丰富,有链码、Zernike炬、夹角链码、Helmholtz描述子等多样的曲线描述方法[8-9]。文献[10]认为曲线匹配的关键是提取准确的拐点；文献[11]利用曲线的角点、序列关系进行匹配；文献[12—14]利用fréchet距离进行曲线间的相似性评估；文献[15]利用离散轮廓评估(DCE)进行匹配识别。多数曲线匹配技术需要提取特征后再进行特征匹配。曲线描述的准确性、全面性、抗干扰能力是这类型匹配的关键。

文献[16]于1992年提出了最临近点迭代算法(iterative closest point，ICP)常用于三维模型的拼接，该算法的实质是数据集间相似信息的最优化配准[17-18]。文献[19]先采用特征点线进行粗匹配、再采用ICP算法获得小差异影像的精确匹配。ICP算法原理简单、不需要提取或描述特征，但其缺点是效率低[20]，容易陷入局部最优的错误。

本文针对大差异影像提出顾及形变的影像边缘ICP匹配算法(iterative closest point of deformation image，ICPDI)，提取影像的长边缘特征作为显著特征，使用ICP算法实现二维线特征匹配，增加几何形变函数应对影像间几何特性差异，从而抑制辐射和几何信息差异，实现影像匹配。

1 ICPDI影像匹配

1.1 影像边缘特征提取

边缘是影像的重要特征，是影像中灰度、纹理分布不连续处的像素组合，由点连接而成，具有一定的稳定性，不易受辐射差异的影响。本文选用Canny算子提取影像边缘，通过平滑、边缘增强、保留梯度最大值、双线性阈值等处理，最终获取影像连续稳定的边缘特征。

Canny算子阈值与影像辐射特性密切相关，不同特性影像需要不同参数才能获得理想边缘。本文设置固定的Canny双阈值，降低高阈值，充分提取强边缘和弱边缘特征，设置较低的低阈值保留影像细节，再按照边缘的长度筛选出长边缘。这一参数设置方式是将阈值与影像辐射特性的相关性降低，符合本文边缘特征匹配的需求，一方面保留了显著特征，另一方面抑制了碎小特征的干扰。

图1的遥感影像为某地新开发区的冬季雪后1 m分辨率影像。采用固定阈值Canny算子(低阈值1，高阈值5，保留线段长度大于20像素)提取影像边缘结果如图1所示。运动场、道路、屋顶等灰度、纹理变化小的区域抑制了短线特征，保留了沿道路的显著长线特征。

1.2 影像边缘ICP迭代匹配

ICP算法常用于三维点集间的匹配，本文将ICP算法用于二维线特征集间的匹配。设待匹配影像的边缘线特征集为P，基准影像的边缘线特征集为Q。匹配过程是寻找集合P与Q之间的最优旋转矩阵R和平移向量T，使得P与Q中的相似特征重合，即

RP+T=Q

(1)

实际匹配中，P与Q不会完全重合，因此式(1)就转换为如下形式

(2)

式中，最优旋转矩阵R和平移向量T使得P与Q之间的对应线特征距离最小为Dmin；Qi为与Pi对应的线特征；n为集合P与Q之间能够成功匹配的线特征个数。影像边缘的线特征ICP匹配具体步骤如下：

(1) 从集合P中取子集Pi∈P，Pi为集合P中的某一条线特征，由连续点构成，设定旋转矩阵R0和平移向量T0参数初值，获得Pi+0=R0Pi+T0。

(2) 计算线特征Pi+0中每个点的法线与基准线特征集Q的交点，形成与Pi+0对应的线特征Qi∈Q。

(3) 基于Pi+0和Qi的对应点关系，通过最小二乘计算获得旋转矩阵Ri+0与平移向量Ti+0。

(4) 对Pi+0进行旋转、平移计算，Pi+1=Ri+0Pi+0+Ti+0，获得线特征Pi+1。

(5) 计算线特征Pi+1与Qi之间对应点的距离均值D。

(6)D若大于阈值Dh(本文中设为0.5像素)，将Pi+1替代Pi+0，返回步骤(2)继续寻找线特征集Q中的对应线特征Qi。

(7) 当D始终大于阈值Dh，迭代次数达到最大迭代次数Lh(本文设定迭代次数50次)则停止迭代，表示匹配失败。

(8)D若小于给定的最小距离阈值Dh，则达到最优解并停止迭代。此时获得两个线特征集间的旋转矩阵R、位移向量T、最小距离Dmin。从Pi+1与Qi间的映射关系逐个计算Qi中符合最小距离Dmin的点，形成有效线特征集QY。遍历P中所有的线特征，得到QY中的有效特征点数numQY和线特征总点数numQ(Q中的点数)，按照式(3)可以获得相似度W如下

(3)

有效特征集的补集是变化地物或噪声，是对匹配计算无效的线特征集，算法在整体距离最近的条件下，能够区分有效和无效的线特征，从而抑制影像数据缺失、噪声等干扰。

1.3 基于形变函数的影像边缘ICP匹配

ICP匹配计算能够精确获取线特征集间的仿射变换参数，但是当影像间存在几何变形时，常规ICP算法会陷入局部最优错误。

本文针对形变影像匹配问题引入几何形变函数K，集合P经过几何形变函数K的变形获得P′，即

(4)

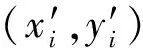
(5)

形变函数和影像边缘ICP匹配的迭代计算流程如图2所示。

图2中的变形模板有5种类型。如图3所示，图3(a)为没有形变的影像；图3(b)—(d)分别为4种变形模板，模板的短边角点可以调整长度以改变形变比例。根据变形模板与图3(a)角点间的点号、坐标对应系，按式(4)可计算12个形变参数a1、a2、a3、a4、a5、a6、b1、b2、b3、b4、b5、b6，用以记录变形映射关系。

在图2流程中，变形函数K遍历4种变形模板和不同的形变参数，以特征间距离最小、相似度值最大作为判据，逐步迭代筛查最优模板和形变参数，逼近最优值。

ICPDI算法是将栅格影像转换成线特征进行匹配，线特征具有易于变形的特点，改变形变函数K将会扩展ICPDI算法对于不同形变的支持能力。

2 试验分析

试验分别从精度、变形、噪声干扰、时相差异等方面验证算法性能。

试验1：图1为基准影像。在图1基础上加入50像素位移形成影像1a，顺时针方向加入10°旋转形成影像1b。匹配结果如图4所示。

试验2：两个时相的影像分别作为基准影像。按照图3(b)的变形模板生成待匹配影像2a、2b，再分别进行匹配，结果如图5所示。

试验3：图1(冬季影像)为基准影像。选择一幅夏季影像经过增加颗粒噪声形成影像3a，增加圆斑形成影像3b。匹配结果如图6所示。

试验4：同一地区4个时相的遥感影像差异巨大。影像4a中道路、学校、操场正在修建，空地较多，主要地物边缘线不完整、不清晰；影像4b中，道路、学校已修好，还存在大面积空地；影像4c是冬季雪后影像，融化中的白雪增加了大量不规则的影像边缘；影像4d中原有空地上新增各式房屋。试验4以影像4b作为基准影像，影像4a、4c、4d作为待匹配影像。匹配结果如图7所示。

试验结果主要参数汇总见表1。

表1 试验主要参数记录

试验1表明本文算法能够在小差异影像匹配中精确获得平移、旋转参数。

试验2可以从图5结果影像观察，形变影像已匹配成功。影像2a与2b相比，相似度W较低，迭代次数较多，说明影像2a匹配质量较差，冬季影像线特征较繁杂，干扰了匹配性能，说明匹配结果与边缘特征的质量有关，需要优化提取影像的主要边缘特征以降低这种相关性。

试验3的待匹配影像受强烈噪声压盖，影像3a的颗粒噪声使边缘线特征产生高频率的抖动，影像3b的圆斑噪声使边缘严重偏离原有位置。比较两次试验的匹配参数，圆斑噪声对于匹配的影响更为严重，导致迭代次数达50次。在强烈干扰情况下仍然能够获得较为合理的匹配结果，体现了算法较强的适应性。

试验4可以从图7结果影像观察，影像4a、4c、4d匹配成功。影像4a与4b匹配计算中，正在修建的道路特征较弱，但依然获得合理的匹配结果，体现了算法依靠整体一致性抑制局部差异的特性。影像4b与4c、4b与4d间的匹配质量较好，相似度较低是由于地物变化导致有效特征数量的变化。

3 结 语

本文针对大差异影像间的匹配问题提出了ICPDI算法，通过试验证明，该算法能够抑制几何变形、辐射差异等干扰获取较稳定的匹配结果和影像间的平移、旋转、变形、地物变化等参数。本文算法扩展了ICP技术在影像匹配领域中的应用，目前依靠迭代次数、特征间距离、相似度等要素综合衡量匹配质量，还需要进一步研究更为简单有效的算法质量评估方法。