一种改进的高精度地图自动配准方法
王 淼,薛宇飞,葛君霞,郭兆钟
(北京四维图新科技股份有限公司,北京 100094)
适用于自动驾驶的道路高精度地图相较普通导航电子地图而言,具有更高精度、更加详细的地图元素、更加丰富的属性,对于无人车定位、导航、控制及安全至关重要,是自动驾驶的核心技术之一[1-2]。为了保证自动驾驶系统的安全性,地图的时效性,即鲜度与精度同样重要。因此,需要持续更新自动驾驶道路高精度地图数据库。而更新地图的关键课题为如何高效地融合多次采集的数据。
由于移动测量的复杂性,测量中的随机误差不可避免,不同时刻或不同设备采集的地图数据不能直接拼接融合在一起。因此,首先需要将两次采集的数据在没有发生变化的地图要素处配准一致,才能通过差分运算,检测出数据之间的真实差异,如车道边线的新增、删除或几何形态变化。
高精度地图数据采集的误差源主要包括:不同时刻卫星信号的差异对GPS接收机定位结果的影响;不同时刻惯导的漂移不同;不同天气对激光雷达采集点云数据的影响等,这些误差来源具有随机性和不确定性。因此不同时刻的采集数据不是简单的线性变换关系,采用传统的线性最小二乘算法实现仿射变换[3],不能满足高精度地图对配准的要求。为提高配准精度,本文提出了一种利用正则化的局部加权薄板样条函数拟合算法实现配准的非线性变换方法,配准效果良好,以3 cm作为配准成功阈值,配准率可达95%以上。通过生产应用,证明该方法完全满足自动驾驶道路高精度地图更新要求。
1 高精度地图配准流程
配准工具的目标是将不同时刻或不同设备采集的同路段高地图数据进行融合。本文将待配准地图数据称为源地图数据,配准的目标地图数据称为目标地图数据,配准后的地图数据称为成果地图数据。
配准实现的基本流程主要包括变换场生成和配准两部分。其中变换场生成阶段先选取合适的同名点,然后利用正则化的局部加权薄板样条函数进行插值,生成最终的变换场;配准时将源地图数据的各要素根据变换场配准到目标地图数据,进而生成成果地图数据。基本流程如图1所示。
2 配准算法
薄板样条函数(TPS)[4]拟合方法在图像配准中应用较多,可以根据离散、稀疏的控制点生成光滑的三维表面[5]。
薄板样条函数是一种常见的插值方法[6],通过在两张图像中找出控制点的方式,应用TPS可以将控制点形变到对应位置,同时给出整个空间的形变矩阵[7]。但由于传统薄板样条函数生成变换场时需要图幅中的所有控制点均参与变换,计算量大且局部变换不一致时配准效果不佳。为避免此弊端,本文采用了一种局部加权薄板样条方法生成变换场。局部加权薄板样条函数原理与薄板样条相似,只是生成变换场时每个控制点只由其临近的N个控制点决定,不受全局其他控制点的影响。N个邻近控制点的选取通过KD树邻近点搜索算法实现[8]。鉴于高精度地图道路要素一般变化比较平缓,在局部加权薄板样条基础上引入了正则化参数。正则化参数与薄板样条弯曲能量之间呈负相关,正则化参数越大,弯曲能量则越小,拟合的曲面越趋于平缓[9-10]。
局部加权薄板样条函数基于生成最小曲率的面来拟合控制点,其二维空间的近似表达式如下
(1)
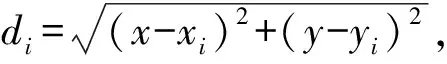
(2)
式中,PTM=0是边界限制条件,保证在无限远处刚性变换为0;K为N×N矩阵;P为N×3矩阵;M和V为N维列矩阵;A为三维列矩阵。各矩阵表达形式如下
(3)
(4)
(5)
(6)
通过解算式(2)可得到未知数M和系数矩阵A。在此基础上,利用式(7)计算薄板样条弯曲能量。
设定一个弯曲能量收敛阈值,如果弯曲能量大于设定阈值,则调整正则化参数σ,重新迭代,直至弯曲能量小于阈值,迭代结束,生成变换场矩阵。
If=WTKW
(7)
在配准过程中,对每个控制点P(xi,yi)赋予一个权值Wi(R),其形式如下
(8)
利用加权平均的方法,对过任一点P(x,y)的所有薄板样条函数取加权平均来确定其对应的各个分量。
其中X值分量映射函数f(x,y)计算如下
(9)
Y分量映射函数g(x,y)为
(10)
Z分量映射函数h(x,y)为
(11)
正则化的局部加权薄板样条拟合法目的是将距离点P(x,y)最近的控制点影响最大,距离越远影响越小。当控制点P(xi,yi)与点P(x,y)的距离大于RiN时,则不计其影响。
3 试验验证
将某工程t1时刻采集的高精度地图数据作为源地图数据,选用t2时刻采集的高精度地图数据作为目标地图数据,利用本文的整套配准算法和线性最小二乘算法作对比试验。其中线性最小二乘算法与本文提出的正则化的局部加权算法实现配准的流程相同,该算法也是在控制点选取之后,利用最小二乘算法生成变换场,从而实现高精度地图的刚性配准。其实现原理如下[2,11]
Y=RX+t
(12)
式中,Y表示变换后坐标;X表示变换前坐标;R为旋转矩阵;t为平移矩阵。具体实现不再详述。
不同要素配准后对比结果如图2—图5所示,其中线性连续要素配准结果如图2—图4所示,点状离散要素配准结果如图5所示。
图2—图5中,浅色线条均代表源地图数据,深色均表示目标地图数据。从图2—图5可以看出,本文配准算法整体贴合度更好,明显优于线性最小二乘算法。为了更好地统计两种算法匹配率情况,对整个工程配准结果中各要素配准成功率进行统计,结果见表1。

表1 各要素配准成功率统计
从表1中可以看出,在相同试验场景和相同判定标准下,本文算法配准成功率较最小二乘算法有了大幅度提升。
为进一步评估算法的配准效果,本文将目标配准地图数据各控制点作为真值,以成果地图数据的各对应点为待验证值,通过统计目标数据与成果数据所有要素对应点之间的距离偏差,以及均方根误差(RMSE),对配准后效果及精度进行评价。配准后数据偏差及均方根误差统计结果如图6、图7所示。
图6、图7中横坐标表示目标地图数据与成果地图数据同名点之间的偏差,单位cm,如0—1表示距离偏差在0~1 cm之间;纵坐标表示对应偏差范围内点数占总点数的比例;RMSE为对应图幅的均方根误差。通过图6与图7的对比结果,可以看出本文算法与目标地图数据的偏差更小,精度更高。
综上,配准前数据存在明显偏差,采用线性最小二乘算法,大部分配准效果较配准前有较大改善,但局部配准效果不佳;而采用本文正则化的局部加权薄板样条算法配准后成果地图数据与目标地图数据贴合更紧密,配准效果较线性最小二乘拟合算法有明显改善。
4 结 语
本文在充分考虑自动驾驶道路高精度地图特征的基础上提出了一种正则化的局部加权薄板样条算法,实现高精度地图的配准,并通过实践验证了方案的可行性。试验结果表明,该方法能有效实现高精度地图数据的配准,有利于缩短高精度地图数据的更新周期,为自动驾驶系统地图的时效性提供了充分的技术保证。

