基于轮廓的侧扫声呐图像配准

李治远，豆虎林，胡 俊，吴子敬，吴永亭

(1. 自然资源部第一海洋研究所，山东 青岛 266061； 2. 山东水利职业学院，山东 日照 276826)

声学探测是高效、精确地调查水体和海床状况最好的方式，甚至常常是唯一可行的手段[1]。在众多声学设备中，侧扫声呐(side-scan sonar，SSS)系统因为低廉的价格，以及可以高效地获取高分辨率海底地貌图像等优点，在海洋科学、海洋工程、水下搜救与目标识别等领域得到了广泛的应用[2]。但由于作业模式及其成像机理的原因，侧扫声呐图像存在局部畸变和位置偏差，按照地理编码结果将不同条带拼接到一起时，存在共视目标错位的问题，不利于地貌信息的准确表达。

针对侧扫声呐图像的配准，许多学者为此作了相关研究。文献[3]提出基于SURF的共视目标分段配准方法，并通过小波变换实现图像融合，该方法顾及局部畸变图像特点，配准后共视目标一致性较好。文献[4]研究了顾及畸变的侧扫声呐条带图像镶嵌方法，提出了分块提取特征思想以及基于薄板样条的局部弹性配准方法，取得了很好的效果。文献[5]研究了基于ORB(oriented brief)算法和KAZE算法的侧扫声呐配准方法，但在配准的过程中未顾及图像局部畸变不一致的特点，当侧扫声呐采用拖曳作业模式或海底线提取不准确时，该方法拼接效果难以保证。文献[6]提出了针对侧扫声呐图像的分层特征匹配算法及基于非线性尺度空间的特征匹配算法，提高了特征点的匹配率。文献[7—8]研究了基于SURF的侧扫声呐图像配准，但同样未顾及不同区域图像变形程度不一致的问题。通过以上分析可以看出，现有关于侧扫声呐拼接的研究大都是先提取特征点，然后再进行特征匹配，最后以某种准则进行图像的融合。但是，侧扫声呐图像存在噪声大、整体细节特征分量少的特点，大量稳定的特征点不易获取，这给配准带了困难。近年来，图像分割领域发展很快，出现了大量优秀的算法，这给侧扫声呐图像的结构化分析带了可能。侧扫声呐图像配准的最终目的就是保证相同目标拼接后轮廓一致，为此，本文提出一种基于目标轮廓的配准方法，期望能对现有配准方法进行补充。

1 配准方法

本文所提出的声呐图像配准方法核心是轮廓点配准及图像弹性变换模型的建立，下面分别对其详细介绍。

1.1 基于形状上下文轮廓配准

在对图像进行分割后，可以很容易地获取不同分割区域的轮廓P={p1,p2,…,pn}，其中，pi∈R2，为轮廓点在图像上的坐标，n为轮廓上的点数。图像配准的目的是找到两幅图像上像素的对应关系，对于图像上的两个轮廓来说就是找到它们边界点的对应关系。边界点的特征描述越丰富、越具有代表性，则在匹配时越不容易发生误匹配。环境上下文(shape context，SC)是一种可以描述丰富特征的描述子，能够表达出周围点相对某一点的分布情况，具有很强的分辨能力，对于各种变形、异常值等具有很强的稳健性，因此，很适合非刚性变换的点位匹配[9]。

对于轮廓上的任意一点pi(如图1所示)，以点pi为圆心的5个同心圆和过该点的6条直径将以半径为r的范围内的区域分割成了60个区域，其中的一个区域如图1中区域A(即式(1)中的bin(k))所示，通过统计落入每个区域除去pi以外轮廓点的个数，得到pi周围点位的分布直方图hi，作为该点的SC描述。为了使SC具有尺度不变性，通常选择所有轮廓点之间的平均距离作为r值。实际计算过程中，圆的个数及直径的个数可调整，每个圆的半径rc满足条件log(rc)=c/log(r)(c=1,2,…,C，C为圆的个数)。

(1)

由于SC是一种表示点位分布的直方图，因此，可以用χ2检验作为度量两个点匹配的损失函数Cij。

(2)

在定义了损失函数之后，两个轮廓之间的配准就变为寻找使得损失函数之和最小时的轮廓点对应关系，而寻找最小损失值是一个双边图配准问题，有很多方法可以解决此问题，本文采用文献[10]中的方法。为了能够稳健地处理异常值，可以向轮廓点集合中添加虚拟的点并赋予其一个恒定的匹配损失值ε，当一个轮廓中的点pi在另一个轮廓中找不到损失值小于ε的匹配点qj时，就分配给pi一个损失值为ε的虚拟点，因此，可以将ε当作一个排除异常值的阈值。

(3)

1.2 基于TPS图像变换建模

通过轮廓配准可以找到轮廓上对应的点对，为了使两幅声呐图像中的对应区域能够重合到一起，还需要建立变换模型。考虑声呐图像存在局部畸变，不能简单地用刚性变换来表示，本文采用薄板样条函数(thin plate spline，TPS)作为变换函数。薄板样条函数能够将空间变换分解为一个全局仿射变换和一个局部非仿射变换[11]，是一种应用较多的弹性变换方法。TPS插值函数可以使弯曲能量函数(如式(4)所示)的值取得最小，函数形式如式(5)所示。

(4)

f(x,y)=v=a1+axx+ayy+

(5)

式中，v表示坐标(x,y)经变换后的横坐标x′或纵坐标y′;U(r)是一个核函数，定义为U(r)=r2logr2，r为两个轮廓对应点对的欧氏距离，通常有U(0)=0。TPS函数有n+3个参数，而f(x,y)=v只有n个方程，需要添加3个约束条件才能求解，即

(6)

综上可得方程式组(7)，方程组写成分块矩阵的形式如式(8)，由文献[12]可知方程组左侧方阵是可逆的，因此，方程是有解的。

(7)

(8)

根据式(8)可分别解出x轴和y轴方向上的变换参数[a1(b1),ax(bx),ay(by),w1,w2,…,wn]T，则一幅图像上的任意一点(x,y)的变换坐标(x′,y′)的计算公式为

(9)

当轮廓点存在噪声时，可通过正则化来放宽插值的精度，实现的方式是使得式(10)取得最小值[13]。

(10)

正则化参数λ是一个正值，控制着平滑的程度。当λ=0时，矩阵块U的对角元素均为零，式(10)退化为精确的插值，薄板样条函数严格经过各参考点；当λ=+∞，式(10)变为一般的仿射变换模型。求解方法是将式中U矩阵替换为U+λI，I是一个n×n的单位矩阵。

1.3 配准流程

声呐图像配准流程如图2所示，首先，对图像A和B进行分割，分割方法不限，只要能够有效地分割出图像中的目标即可；其次，统计分割结果中目标的轮廓点集合，寻找对应的轮廓，方法有很多，如通过计算轮廓Hu矩、成对几何直方图(pairwise geometrcal histogram，PGH)等进行匹配，在匹配的过程中可根据地理位置坐标缩小搜索范围，加快匹配过程；然后，根据找到的对应形状，基于形状上下文进行轮廓配准，得到轮廓上对应的点对；最后，基于薄板样条函数建立弹性变换模型，同时进行数据融合，值得注意的是，两幅图像都应是侧扫。

2 试 验

为验证本文方法的有效性，分别进行模拟试验及使用野外实测侧扫声呐图像数据进行试验。

2.1 模拟试验

模拟试验采用I1、I2、I3及I4等4幅图像进行(图3中C1列)，其中,I1、I2为模拟图形，且I1为规则五角星、I2为不规则图形；I3、I4为侧扫声呐图像，且I3为凹陷目标、I4为凸起沉船目标。使用imgaug图像增强库对图像进行随机的分段仿射变换，来模拟图像的局部形变，参数scale取0.01～0.06之间的随机数，变换后的结果如图3中C2列所示。可以看出，4幅图像均得到了不同程度的局部变形，模拟试验通过变形前后轮廓匹配并计算变换参数，且使用变换参数对变形后的图像进行恢复，然后与原始图像进行比较，以评价本文提出算法的有效性。

首先采用OpenCV中的grabcut分割算法对图像进行简单的分割并提取轮廓，结果如图3中C3列所示；然后，计算轮廓点的形状上下文并使用1.1节描述的算法进行轮廓点匹配，其中ε取值0.15，匹配的结果如图3中C4列所示；最后，在找到对应的轮廓点之后使用1.2节中描述算法进行变换参数计算，其中λ取值0.25，根据计算得到的变换参数对目标轮廓进行恢复，结果如图3中C5列所示。其中黑色点表示图像恢复时的变形情况，从图像上可以看出,进行分段仿射变换的图像中目标的轮廓经过恢复变换后与原始图像中目标的轮廓重合度较好。对于图像I4的结果进行局部放大,如图4所示，其中(b)为轮廓点匹配结果的局部放大图像，可以看出大部分轮廓点对得到了较好的匹配；(d)是根据变换参数恢复过来的图像，可以看出经TPS恢复的目标形状能够较好地与原始图像保持一致。

为了量化说明试验结果，分别对每个图像原始轮廓点数、分段仿射变换图像上目标轮廓点的个数、匹配上的点对数，以及图像恢复变换后与原始图像上对应轮廓点之间的不符值中误差进行了统计，统计结果见表1。从表中可以看出，通过目标形状环境上下文匹配可以匹配到密集的点对，而且使用TPS插值函数函数建模，能够有效描述图像的局部形变，经TPS恢复的目标轮廓中误差最大为1.72像素，最小为沉船，0.77像素。

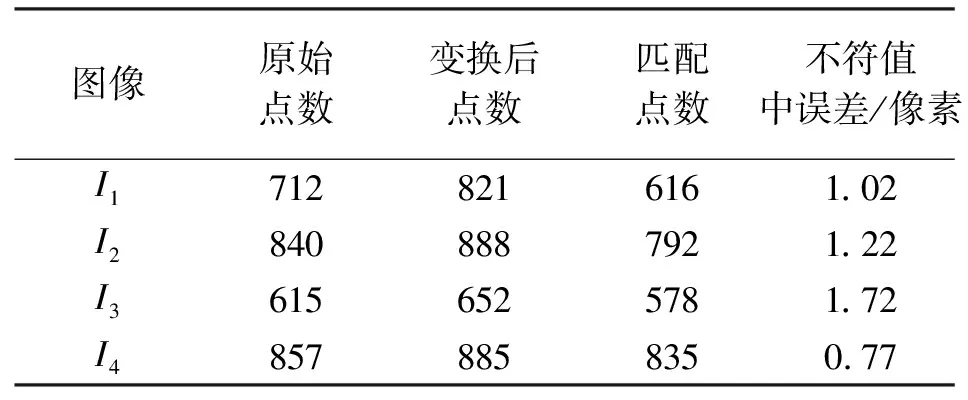
表1 匹配与变形恢复结果

2.2 实测图像试验

使用实测侧扫声呐数据进行试验，试验的步骤及参数与模拟试验相同，不同的是图5中C1列和C2列的侧扫声呐图像来自于不同测量条带对于相同目标的测量结果。可以明显地看出，由于复杂的水下测量环境、侧扫声呐姿态改正不完全及测量角度不一致等问题，侧扫声呐对于同一目标的测量结果具有较大的差异，尽管有较大的畸变，但是整体上还是能够看出一定的相似性。以C1列的图像为参考图像，将C2列的图像作为需要变换的图像，在经过形状上下文的配准及TPS插值函数建模之后，C2列的图像变换结果如C5列所示，尽管图像局部畸变很大，但是经过配准并形变建模后，图像可以很好地恢复成参考图的形状，需要说明的是，C5列的图像仅仅是由C2列图像上每个像素点经TPS计算出对应位置取整填充所得，因此，图像上存在空缺，用灰度值0填充。

同样的，对试验结果进行量化统计，结果见表2，成功匹配的点对数比较密集，最大不符值中误差为2.3像素，因此，通过TPS建立的变换模型能够有效地描述侧扫声呐图像的局部畸变。

表2 实测侧扫声呐数据匹配及变形恢复结果

3 结 语

针对侧扫声呐图像存在局部畸变的问题，本文提出了一种基于轮廓的侧扫声呐图像配准方法。试验表明，本文方法不仅可以高效地获得共视目标轮廓上点的对应关系，从而获得大量的配准点对，而且能够通过TPS函数对局部变形进行有效建模，这对于后面侧扫声呐图像相邻条带拼接，以及侧扫声呐图像与多波束地形叠加具有重要意义，是对现有基于SURF算子方法的补充。但同时也要注意到，本文方法需要准确地分割结果，当图像比较杂乱时，效果会受到影响，未来可考虑通过增强并利用边缘信息来改善算法性能。