半参数模型对我国白银期货风险价值的估计

文/张淑娟

论文使用几种参数及半参数GARCH-VaR 模型，对我国的白银期货市场进行价值风险的估计。通过检验结果发现GARCH 模型结合非参数分位数的半参数方法，具有更好的估计效果。因此文中使用的这种半参数估计方法，可以对于我国的白银期货市场的风险预测具有一定的参考意义。

白银从最初的发现到至今已有5000 多年的历史。其属性慢慢从货币属性过度到当今的工业及金融属性。我国在2012 年建立白银期货市场，由于其建立时间比较短，因此我国贵金属市场还有一些可待完善的地方。在某些情况下，白银比黄金的价格波动波动要更大一些，风险也就更大一些，因而无论对于投资者还是风险监管部门，都需要合适的模型预测风险，从而规避或者降低风险，减少损失。

相比较黄金期货市场的相关研究，白银期货市场的研究要少一些，部分学者研究了两者之间的价格关系。董宇博在2013 年运用协整检验与格兰杰因果检验，对我国白银期货价格与国际白银期货价格之间的关系进行了实证研究；张雪峰2016 年对金银价格数据进行分析，通过研究结果显示金银价格之间存在着长期的正相关关系；朱震于2016年基于MC 和极值理论对黄金期货的风险价值进行了度量；唐成晓在2012 年通过使用混合极值模型对白银市场进行了风险测度；另外陈玉秋在2016 年探讨了我国白银期货的套期保值比率,胡巧珍等人于2018 年对中国白银期货市场的发展进行了研究。通过对文献的整理发现，当前对于我国白银期货市场风险价值研究的论文比较少，因此本文将从风险价值模型入手,使用参数及半参数GARCH-VaR 模型,对我国白银市场进行风险测度。通过检验发现，文中使用的模型，可以为我国白银市场的风险管理及白银投资者，对于风险价值估计的提供理论参考。

模型原理：VaR估计与非参数核密度分位数

VaR 定义、计算基本原理及检验方法：

VaR（Value at Risk)可以翻译为“在险价值”，也有将其称为“风险价值”。它最初是由J.P.Morgan公司提出，是一种对金融资产的风险进行测度的工具。VaR 可以应用于证券、保险公司、银行等等金融机构。它是指在金融资产价格正常波动下，在一定的置信水平下，某一种金融资产或者几种资产的投资组合价值在将来的某一段时期内，可能承受的最大价值损失。VaR可以通过下面的数学方式来表达：

用tr表示某一金融资产在时刻t的收益率，当时表示资产获得收益，相反表示的是资产有损失，VaR 关注的随机变量tr的左尾分布。令表示随机变量tr的分布函数，对于置信水平可以表示为：

或

下面来具体介绍文中所使用VaR 的估计方法。

（1） 对于我国白银期货预期收利率的设定为ARMA（1，1）模型，由于其具有异方差性，波动率使用GARCH 模型来估计，即

（2）新息项分位数的估计

白银期货市场受诸多因素的影响，特定的某种分布不一定完全符合数据特征，比如正态分布，学生t 分布等等。文中对于新息项tε的分位数，建议使用非参数核密度分位数的方法来估计，因为这种方法不需要设定具体的分布函数，完全由历史数据的特征拟合出来，这样不存在分布函数的误设问题，使得模型的估计更加具有可靠性。下面是对其简单的介绍：

设定随机变量X的总体密度函数为

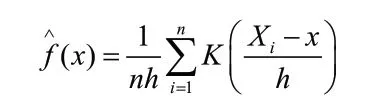
其中X1,X2,...Xn为观察X得到的一组独立同分布样本，K表示核函数，文中使用Epanechnikov 核函数，由于其在理论上可以使得估计量的积分均方误差最小，h为光滑参数带宽，文中使用交错鉴定法来确定其最优值。由概率论的知识可知，通过对随机变量的密度函数的积分可以得到分布函数，因此对核密度函数进行积分，就可以得到非参数核分布函数

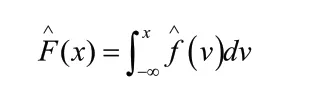
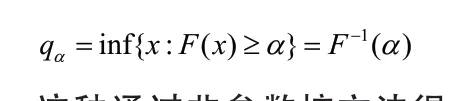
这种通过非参数核方法得到的分位数，不受随机变量密度函数形式的限制，不存在误设的问题，具有一定的稳健性。

（3）VaR 模型的检验

文 中VaR 的 检 验 方 法 采 用Kupiec(1995)提出的LR 检验法，即似然率检验法。由于其简单易行可靠，这是一种可以广泛使用的方法。假定置信水平为1-α，实际观测的天数为T，损失超过VaR的值称为失败，失败天数为N，那么失败率记为期望概率为零假设为，备择假设为通过检验失败率是否拒绝零假设来确定模型的可靠性。似然比率方程记为：

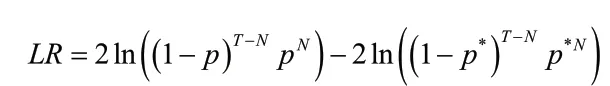
对白银期货价值风险的实证分析

对于前面给出VaR 的计算公式，文中通过设定固定的密度函数形式与非参数密度方法进行对比，所以新息项分别设定服从正态分布(简称Norm 分布)、学生t分布与非参数核密度方法来计算分位数，再结合GARCH 类模型来计算VaR。

（一）数据选取及处理

文中的使用的数据来源于大富翁数据中心，是上海期货交易所从2012 年5月10 日至2019 年5 月26 日的白银期货数据，共计1709 组。论文采用的为日收盘数据，收益率使用对数收益率，具体的计算公式为：为白银期货日收盘价，对于数据的处理及模型估计，论文使用R 软件进行估计。

表1 单位根检验：p=0.01

表2

表3 Kupiec检验

（二）GARCH 模型参数估计

在对模型估计之前，先对白银期货收益率数据进行平稳性检验：单位根检验，检验结果如表1。

对残差进行ARCH 效应检验，通过检验结果可知其收益率具有异方差，因此应用GARCH 模型来估计波动率。由于金融数据具有尖峰厚尾性，所以在对GARCH模型估计时，设定收益率的新息项服从t分布。下面为GARCH 模型的参数估计结果及其对应的P 值。

从上面的参数估计值及概率P 值可以看出GARCH 波动模型中各项系数除了均值估计，其余参数均比较显著。然后再一次对新息项进行了ARCH 效应检验，检验结果通过，说明不存在异方差。下面在新息项分别设定服从正态（Norm）分布、t 分布与不设定分布函数形式的非参数核密度分位数方法，对VaR 进行向前一天的估计及检验。

（三）VaR 计算结果的检验

从表3 的检验结果可以看出，在三种置信度下，使用非参数核密度估计的分位数方法估计效果最好，与真实值的最为接近，而正态分布在置信度为0.975 与0.99时均低估了风险，学生t 分布在置信度为0.95 与0.975 时高估了风险，这与两种密度函数的特征相关。而金融数据的厚尾性，使得两种密度函数不能很好的描述白银期货的特征，非参数密度由数据拟合，避免这种误设，是一种可以广泛使用的方法。

当前的白银市场还处于熊市中期，白银的价格正处于低位震荡阶段，全球的经济面临着周期性衰退，因此中长期投资贵金属对于抵御通货膨胀还是一种不错的方式。投资都伴随着风险，那么对未来的风险进行适当的预测是很有必要的。文中使用非参数分位数方法是一种完全由历史数据拟合的方法，避免了对收益率服从分布函数的设定，不存在分布函数的误设问题。然后再通过结合GARCH 模型对白银期货VaR 进行估计，对风险监管部门或者投资者提供了一定的参考价值。但是模型的估计是基于历史数据的基础上，对于一些金融市场突发事件对数据冲击的影响是无法估计的。因此，对于风险的估计要使用模型并结合当前的市场形式，综合对风险进行考量。