平面几何竞赛题解题思想方法初探

四川师范大学数学科学学院(610011) 申 涛 张 红

一、研究背景

数学竞赛是发现数学人才的有效手段之一.数学竞赛与体育竞赛相类似,它是青少年的一种智力竞赛,所以苏联人首创了“数学奥林匹克”这个名词.在类似的以基础科学为竞赛内容的智力竞赛中,数学竞赛历史最悠久,参赛国最多,影响也最大.

现代意义上的数学竞赛是1894年从匈牙利开始的.除因两次世界大战及1966年事件而停止了7届外,迄今已举行过90届.苏联的数学竞赛开始于1934年,美国的数学竞赛则是1938年开始的.这两个国家除第二次世界大战期间各停止了3年外,均已举行过50多届.其他有长久数学竞赛历史的国家是罗马尼亚(始于1902年)、保加利亚(始于1949年)和中国(始于1956年).一些重大数学竞赛的优胜者,大多在他们后来的事业中卓有建树.因此,世界发达国家都十分重视数学竞赛活动.

最近十余年来,我国中学数学竞赛活动蓬勃发展,其影响越来越大,特别是我国中学生在影响最大、水平最高的国际数学奥林匹克竞赛中,多次荣登榜首,成绩令世人瞩目,充分显示了中华民族的聪明才智和数学才能.

纵观我国初中数学竞赛的题目分类,以几何、代数、数论、组合四类为主.在《2017年全国初中数学联合竞赛试题》中,第一试(A)选择题的第2题、第4题、第5题,填空题的第2题,第二试(A)的第二大题均是几何题,合计53分,约占总分140分的37.9%.若按几何、代数、数论、组合四类各占25%来比较,37.9%远远超过了25%的平均比例.题型分类所占比例每年应所差不大,并且在高中数学联赛中几何题所占比例也不低,笔者这里就不再选取其他年份加以验证.另外还可以看出,在《2017年全国初中数学联合竞赛试题》中,第一试(A)三道大题几何题位于第2题,第二试(B)三道大题几何题位于第3题,可见几何位于较重要、较难题型位置.

综上所述,在数学竞赛中,学生是否能够很好把握几何题型的做题思想方法,是取得分数的关键因素之一.故数学竞赛几何题的解题思想方法也极其值得学者、教师进行深入研究.

二、研究分析

笔者查阅相关文献资料并加以归纳总结后研究发现,在数学竞赛几何题的解题思想方法可以从大的方向分为以下三类,即初等几何思想方法、高等几何思想方法、代数思想方法.

1.初等几何思想方法

笔者认为的“初等几何思想方法”是,在欧几里得几何的公理化体系中,运用相关性质解决相应问题.也就是用中学课本上我们学习的如三角形的性质、平行四边形的性质、圆的性质等,还有一些平面几何的重要定理,如托勒密定理、定差幂线定理、梅涅劳斯定理、共边比例定理、分角定理等,来解决相应几何问题.

例题1已知△ABC与△A′B′C′的三边分别为a,b,c与a′,b′,c′,且∠B=∠B′,∠A+∠A′=180°.求证：aa′=bb′+cc′.

证明如图1,作△ABC的外接圆,过点C作CD//AB,交圆于点D,连结AD、BD.因为∠A+∠A=180°=∠A+∠CDB,∠B′=∠B=∠BCD,所以∠A′=∠CDB,∠B′=∠BCD,所以△A′B′C′相似△DCB,于是即所以在四边形ACDB中,由托勒密定理得AC·BD+AB·CD=AD·BC,即因为AB//CD,易知AD=BC=a.即证即aa′=bb′=cc′.

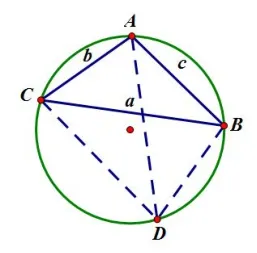
图1

例题1所用到的主要知识点为,托勒密(Ptolemy)定理：圆内接四边形中,两条对角线长度之积等于两双对边乘积之和.注意到例题1所求证等式形式与托勒密定理相似,结合已知条件考虑构造圆、添加辅助线,使用托勒密定理.

托勒密定理是初等几何中圆一部分的重要定理之一,例题1除了用到托勒密定理,同时用到了平行线内错角相等、三角形相似性质、圆内接四边形对角和性质等,这都是初等几何常用的一些重要性质与定理.

通过例题1我们还可以看出,在中学数学竞赛中几何题是相对较难的题型,运用什么定理,如何添加辅助线,这都是做题的关键.托勒密定理本身的内容看似很简单,但用到做题上,如何用,何时用,这都需要日积月累的做题实践.运用“初等几何思想方法”做竞赛几何题时,对于常用的定理、性质一定要牢记于心,并要学会迁移类比,对于几何题的关键“添加辅助线”,要在做题中善于总结经验.

2.高等几何思想方法

笔者认为的“高等几何思想方法”是,运用高等几何的数学思想,如仿射几何、射影几何,来解决初等几何问题.即解决问题不再是在欧氏几何体系之下,而是可以如在射影几何的公理体系之下解决初等几何的问题.这也是当下一些知名学者比较关心的高观点下的中学数学.也许可能让我们更加清晰的看出问题的本质,从“不识庐山真面目”到“会当凌绝顶,一览众山小”的飞跃.

例题2(蝴蝶定理)如图2,设PQ是圆的弦,M是弦PQ的中点,通过M任意作两条弦AB和CD,设AD,BC交PQ于T,S,求证：TM=MS.

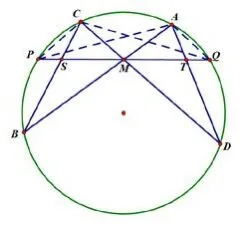
图2

证明如图2,连结C,P;C,Q;A,P;A,Q.对于以C为中心的线束,被直线PQ所截,得C(CPCD,CBCQ)=(PM,SQ).同样,以A为中心的线束,被直线PQ所截,得A(APAD,ABAQ)=(PT,MQ).由同弧所对的圆周角相等,得所以又因为M是PQ的中点,故PM=MQ.所以把TQ=TM+MQ,PS=PM+MS代入上式,得再由PM=MQ知MS=TM.

例题2中所用到解题知识,如中心投影的线束,交比性质等都已不属于中学所学欧氏几何的范畴了,而是属于高等几何分支射影几何体系的知识.从证明的过程可以发现,证明简洁流畅,条理清晰,如果要用初等几何本身的知识去证明会非常的困难.

1872年,克莱因在《关于现代几何学研究的比较评论》一文中总结了射影几何、仿射几何以及其他几何在当时的发展结果,明确地表述了构成这些几何的普遍原则,给出了几何学的近代定义,即考虑空间的任何一个变换群G,研究G的一切不变性和不变量就构成了一种几何.根据这个观点,研究在正交群下图形的不变性和不变量的学科称为欧式几何学.类似地,仿射群对应的几何叫仿射几何,射影群对应的几何叫射影几何.从群的包含关系来看,仿射几何是射影几何的子几何,而欧氏几何又是仿射几何的子几何.就几何学包含的内容多少来看,欧氏几何内容最丰富,仿射几何次之,射影几何的内容最少.在欧氏几何里可以讨论仿射性质和射影性质,在仿射几何里可以讨论摄影性质而不能讨论欧式性质.这让我们对于中学竞赛里面的几何题运用“高等几何思想方法”解题提供了理论依据.如例题2中用到的“线束”知识.

3.代数思想方法

笔者认为的“代数思想方法”是,运用代数学的方法解决几何问题,如建立直角坐标系计算、向量法等等.这也是数学中数形结合重要思想的体现.

例题3在锐角△ABC中,BD是AC边上的高,E是AB边上的一点,满足∠AEC=45°,BD=2CE,且DE//BC.求证：CE=AC+AD.

证明如图3,过点C作CE⊥AB,交AB于点F.设AD=x,CE=a,则在Rt△CEF中,∠CEF=45°,故EF=由于Rt△ACF相似Rt△ABD,从而故因为DE//BC,所以从而解得故进而AC+AD=a=CE.

例题3显然是一道几何证明题,但我们通过解题过程可以看出,整个过程更像代数题目的量化计算,而不是用几何本身的定理性质加以证明,这样可以避免很多较难的思考,直接通过长度之间的和差关系进行证明.并且采取了设置中间变量x和a,我们并不需要求出x和a的具体数值,只是为了证明出最后的结果,这也是一种证明的有效手段方法.

正如华罗庚教授说的那样：“数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休.”竞赛几何题中,运用代数学的方法,正是数形结合思想的完美体现,同样做代数题的时也可以考虑用几何学的方法解题.

三、研究结论与启示

对于笔者梳理的数学竞赛几何题的解题思想方法,即初等几何思想方法、高等几何思想方法、代数思想方法.每种方法各有各自的优势,也有各自的缺点.

初等几何思想方法运用的欧氏几何公理体系下的定理性质解决问题,对于中学生来讲,这更为熟悉,但正像数学家克莱因提出的欧氏几何是仿射几何的子几何,亦是射影几何的子几何,包含内容丰富,对于那么多定理与性质如何选择也是做题的困难之处.

高等几何思想方法运用更为一般的几何学知识解题,如用射影几何知识解题,一道看似很难的题,有可能几步就被解决了,但对于中学生来讲,高等几何并不是中学的知识,如果想要用高等几何知识解题,那就必须要付出更多的时间进行学习,同时,高等几何富含知识越来越少,定理性质越来越一般,解题时也可能忽略题目的细节所在.

代数思想方法有可能避免了添加辅助线,减轻了题目的难度,但也要因题而异,有的题目本身用初等几何的定理性质就可以很快解决,用代数运算反而会增加做题时间,显得更加繁琐.

总之,对于竞赛几何题：“没有最好的方法,只有最适合的方法.”用自己最熟悉的知识体系,在最快的时间内,做对题目,即达到目的.

由于笔者学术水平有限,对于竞赛几何题的解题思想方法仅进行了简单的梳理总结和分析,希望能起到一个抛砖引玉的作用,能给竞赛教师和学生一些经验启示,并在附录作了一份《竞赛几何题解题思想方法》教学设计,仅供参考.

四、附录：教学设计

《竞赛几何题解题思想方法》教学设计

1.教学目标

1.知识与技能目标

(1)掌握竞赛几何题的三种解题思想方法;

(2)对于一道竞赛几何题尝试用两种或三种方法分别解题.

2.过程与方法目标

从一道竞赛几何题出发,引导学生从不同方向进行思考解题,加深学生对竞赛几何题解题思想方法的认识.

3.情感与态度目标

从学生熟悉的竞赛题目出发,让学生体会学习过程,又体现知识的应用过程,激发学生学习兴趣,锻炼逻辑思维,处理问题的能力,有利于学生理性处理身边的事物,培养一种社会责任感.

2.教学重点、难点

(1)重点：竞赛几何题的三种解题思想方法.

(2)难点：高等几何思想方法解决竞赛几何问题.

3.教学方法和手段

基于本节课的内容的特点和学习竞赛学生的心理及思维发展特征,在教学中选择讲授法、讨论法和总结法相结合.与学生建立平等融洽的互动关系,营造合作交流的学习氛围.

4.教学过程

环节一例题1分析讲解,运用“初几”和“高几”两种方法

问题1：在初等几何上我们学习了很多定理,哪位同学还知道赛瓦定理得内容是什么?

问题2：对于“完全四边形”、“调和四边形”、“调和点列”这些概念大家有了解吗?

设计意图所选择的典型例题1运用“初等几何思想方法”需要用到赛瓦定理,故先复习定理本身内容;另外运用“高等几何思想方法”要先讲解基础知识,提出一些学生从未听过的概念名词,激发学生学习兴趣.

所涉及知识点

1.赛瓦定理：在△ABC内任取一点O,延长AO、BO、CO分别交对边于D、E、F,则.(如图4)

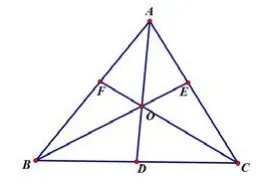
图4

2.调和点列：对于线段AB的内分点C和外分点D满足则称点列A、B、C、D是调和点列.

3.完全四边形：两两相交,且没有三线共点的四条直线及它们的六个交点所构成的图形叫完全四边形.

例题1在△AEF中,B、D分别为边AE、AF的中点,连结BF、DE交于点C,连结AC延长交EF于M.求证：M为EF中点.

法一初等几何思想方法

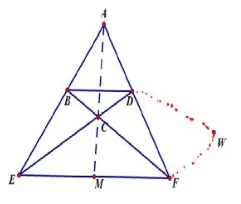
图5

法二高等几何思想方法

如图5,在完全四边形ABCD中,E、M、F、W∞成调和点列,所以即ME=MF,则M为EF的中点.

讲解分析通过一道竞赛几何题用“初等几何思想方法”和“高等几何思想方法”两种方法讲解,让学生一目了然的理解两种方法各自的优势与特点.

例题1两种证明方法思路都比较简明,法一需要很好的掌握赛瓦定理,法二需要学生打破欧氏几何公理体系的范畴,在欧式几何中两条平行线是没有交点的,而在射影几何公理体系下,两条平行线是交于无穷远点的,这样就能很快证明出结果.

环节二例题2分析讲解,运用“初几”和“代数”两种方法

问题1：在初等几何上最重要的图形之一就是三角形,三角形的五心分别是?五心分别有哪些重要性质呢?

问题2：平面向量基本定理的内容是什么呢?

设计意图所选择的典型例题2运用“初等几何思想方法”需要用三角形五心知识,故先复习相关性质内容;另外本题“代数思想方法”主要用到平面向量知识,故先复习回忆最重要的知识点平面向量基本定理.这两种方法所用到的知识都是学生非常熟悉的,故不需要用很长时间进行复习.

例题2设O为△ABC的外心,AB=AC,D是AB的中点,G是△ACD的重心.求证：OG⊥CD.

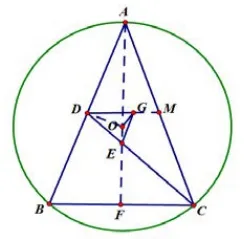
图6

法一初等几何思想方法(利用垂心性质：两⊥⇒第三⊥)如图6,F、D分别为AB、BC的中点,有E为△ABC的重心.所以CE：ED=2：1.又G为△ACD的重心,所以CG：GH=2：1,所以EG//DH.因为OD⊥DH,所以OD⊥EG(1),因为G为△ACD的重心,所以M为AC中点,所以DM为中位线,又因为AF⊥BC,所以AF⊥DG,即AE⊥DG(2),由(1)和(2)可得,O为△DEG的垂心,所以OG⊥CD.

法二代数思想方法(结合向量法计算证明)

讲解分析通过一道竞赛几何题用“初等几何思想方法”和“代数思想方法”两种方法讲解,同样可以像例题1那样让学生一目了然的理解两种方法各自的优势与特点.

例题2两种证明方法可以看出法二的代数法利用向量进行机械计算即可,思考的过程相对法一少了许多,但这也要求学生对平面向量基本定理能有深刻的理解.

环节三总结反思,作业布置

通过两道竞赛几何例题让学生体会三种思想方法,课后可让学生在以前做过的竞赛几何题运用不同方法再进行求解求证,鼓励他们下节课展示给全班,这样也可以让他们对竞赛几何题有更多的求知欲与学习兴趣.